Определение натуральной величины отрезка
Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.
Содержание
- Метод прямоугольного треугольника
- Способ параллельного переноса
- Поворот вокруг оси
Метод прямоугольного треугольника
Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.
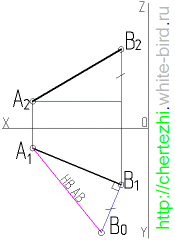
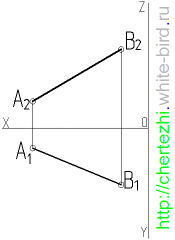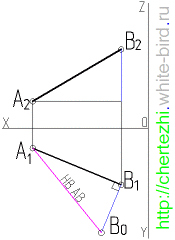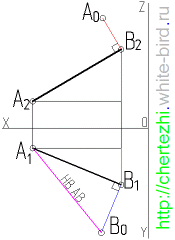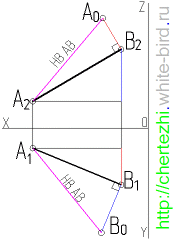
Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A0A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A0 равен величине ZA – ZB, то есть разности удаления точек A и B от горизонтальной плоскости П1.
Откладываем A’A0 = ZA – ZB перпендикулярно A’B’. Затем проводим гипотенузу A0B’ треугольника A0A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.
Способ параллельного переноса
Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П1, то длина его проекции E’F’ не изменится, когда она займет новое положение E’1F’1 (как это показано на рисунке ниже).
Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.
Пример построения
Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’1F’1 = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»1 и F»1. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.
Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.
Поворот вокруг оси
Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.
Пример построения
Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’1N’1, параллельное оси X.
По линиям связи находим точку M»1. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.
Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»1 и M»1 искомым отрезком. На рисунке он выделен красным цветом.
Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.
|
Разделы Уроки по теме Рекомендуем |

Как определить натуральную величину отрезка? Автор: Moroz Дата: 2010-11-08
Сегодня мы рассмотрим один из самых простых элементов теории, но важность его такова, что без него решение большинства задач по начертательной геометрии не представляется возможным. Если вы не знаете, как определить натуральную величину отрезка, то вы никогда не сможете доказать преподавателю, что решили задачи самостоятельно. Задача на определение натуральной величины отрезка в начертательной геометрии встречается как сама по себе, так и в качестве вспомогательных построений при решении сложных комплексных задач. В любом случае, каждый студент, который планирует получить зачетэкзамен по начерталке, обязан уметь определить натуральную величину отрезка, причем быстро и без заминок. Имея две проекции прямой частного положения мы всегда можем определить натуральную величину любого отрезка отложенного на этой прямой. Для этого используется метод прямоугольного треугольника. На рисунке в начале статьи мы определили натуральную величину отрезка АВ построив прямоугольный треугольник на горизонтальной плоскости проекции, но вы должны знать, что построить прямоугольный треугольник мы можем как на горизонтальной, так и на фронтальной плоскостях. Это показано на анимированном рисунке ниже — на нем мы сначала определили натуральную величину АВ на горизонтальной плоскости проекции, а затем на фронтальной Коротко же алгоритм определения натуральной величины отрезка сводится следующему: на любой проекции через любую из конечных точек отрезка проводят перпендикулярную прямую, и на ней откладывают расстояние, равное разнице значений по оси ординат этих двух точек на противоположной плоскости проекций. Т.е. если треугольник строим на горизонтальной плоскости, то разницу значений ищем на фронтальной, и наоборот. Если что-то непонятно из этого описания, то рассмотрев внимательно рисунок вы окончательно поймете, что имелось ввиду.
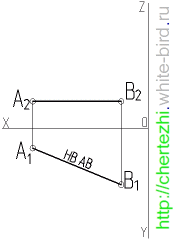
Как видите, ничего особо сложного в этом приеме нет, но знать его очень важно, и не менее важно уметь его применить, как минимум до получения зачета по начертательной геометрии и инженерной графике Особым случаем этой задачи является определение натуральной величины отрезка лежащего в частном положении — например параллельно горизонтальной плоскости проекции. Тогда на его горизонтальная проекция будет сама по себе натуральной величиной и никаких дополнительных построений для ее определения не требуется: Внимание! Для этой темы есть видеоурок. Просмотров: 208489 Вы можете сказать «спасибо!» автору статьи: пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам» или или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.
А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны: Комментарии: спасибо) все понял за 10сек) Спасибо Вам!!!Чтобы я без вас делал Спасибо большое,всё понятно!) Спасибо, наконец-то понятно!!! Спасибо огромное:) все ясно и понятно:) СПАСИБО!!! Я наконец то поняла!думаю сдам без косяков!!! Всегда хотел донести до молодого поколения основы, которые отчего-то не могут донести штатные преподаватели. Успехов в учебе, всем сказавшим «спасибо»! А также и тем кто забыл сказать, но понял тему! Спасибо. Наконец-то понял. Удачи завтра мне. спасибо большое,сразу понял Спасибо. Я все понял, и теперь я успешный дотер, который не пошел в армию, потому что все сдал. Спасибо, все понял, а как на третьем виде строить? или там нельзя? spasibo bolshoe Забегайте! Тут еще много полезного:) Спасибо огромное! Диана, спасибо вам за желание разобраться! Удачи! Просто спасли!Огромное спасибо! Ну… Примерно для этого я все это и пишу:) удачи! Спасибо огромное, очень хорошее поясняющее видео!) спасибо большое, обьяснения очень хорошие . Всё доступно и понятно. Спасибо. Особенно за анимашку) Спасибо большое! Всё объяснено просто и главное понятно! Группа ЭМ-36у благодарит вас за простое и понятное обьяснение Согласен с предыдущим оратором! Приветы всем, кто хочет сам разобраться в предмете! Ищите меня во Вконтакте — ссылка в правом столбике выше. Подписывайтесь, вступайте в группу, будет нескучно и полезно для домашних заданий! Покуда вы будете в этом заинтересованы — совершенно бесплатно! Уникально, так сказать да-да-да!!! Мужики, ну вы даете https://vk.com/XXXX_XXXX
Добавьте свой комментарий: |
Последние уроки Как построить диметрию детали? Построение наклонного сечения, заданного на виде слева Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей. Наша почта: zakaz@trivida.ru Наша страница в ВК: Случайный комментарий Надя: Огромное вам спасибо! вы меня спасли! |
-
Как определить натуральную величину отрезка прямой общего положения.
Прямая, не
параллельная ни одной плоскости проекция,
называется прямой общего положения.
Натуральная
величина отрезка прямой общего положения
определяется величиной гипотенузы
прямоугольного треугольника, построенного
на одной из проекций как на катете.
Второй катет треугольника равен разности
расстояний концов отрезка до плоскости
проекций на которой взят первый катет.
-
Как определить углы наклона прямой линии к плоскостям п1 и п2.
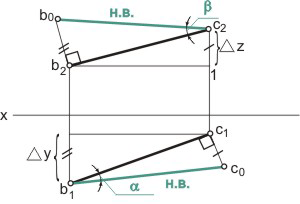
Угол наклона
отрезка прямой к плоскости проекций –
угол, противолежащий катету треугольника,
равному разности расстояний концов
отрезка (∆y).
α — угол наклона отрезка к плоскости П2
можно определить из прямоугольного
треугольника.
Угол наклона к П1
(ниже оси х на эпюре) определяется как
угол между отрезком А1В1
и натуральной величиной этого отрезка.
Угол наклона к П2
(выше оси х на эпюре) определяется как
угол между отрезком А2В2
и натуральной величиной этого отрезка.
-
Главные линии плоскости.
1.Горизонтали h —
прямые, лежащие в данной плоскости и
параллельные горизонтальной плоскости
проекций.
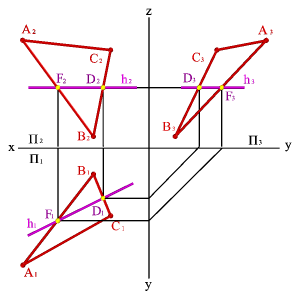
2.Фронтали f — прямые,
расположенные в плоскости и параллельные
фронтальной плоскости проекций.
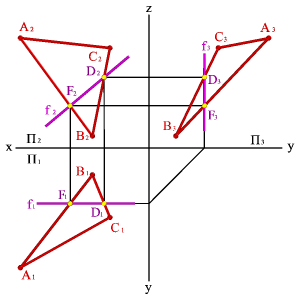
3.Профильные прямые
р — прямые, которые находятся в данной
плоскости и параллельны профильной
плоскости проекций.
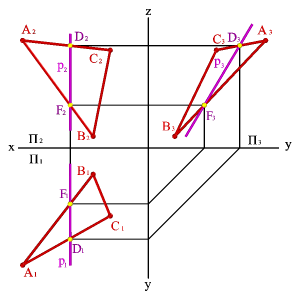
4.Линия наибольшего
наклона к горизонтальной плоскости
проекций называется линией ската.

-
Проецирующие плоскости.
Плоскость частного
положения — плоскость проходящая через
проецирующие прямые, т.е. перпендикулярная
к одной или одновременно к двум основным
плоскостям проекций. Если плоскость
перпендикулярна только к одной плоскости
проекций, то она называется проецирующей
плоскостью. Существует три вида
проецирующих плоскостей:
1.Горизонтально-проецирующая
плоскость — перпендикулярна к П1.
И поэтому проецируется на нее как прямая.
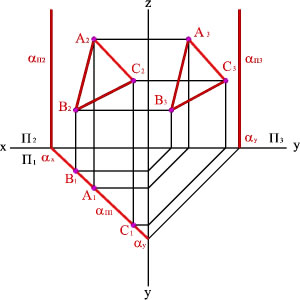
2. Фронтально-проецирующая
плоскость — перпендикулярна к П2.
И поэтому проецируется на нее как прямая.
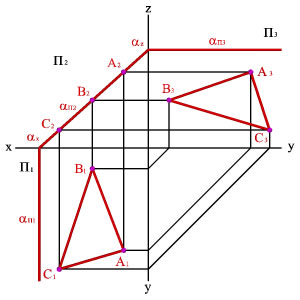
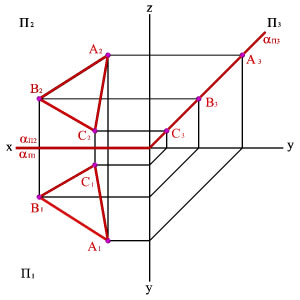
3. Профильно-проецирующая
плоскость — перпендикулярна к П3.
И поэтому проецируется на нее как прямая.
На обычном ортогональном чертеже, когда
плоскость П3
не используется, профильно-проецирующая
плоскость выглядит как плоскость общего
положения.
-
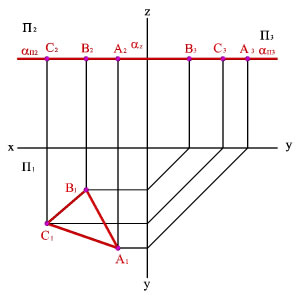
Линии уровня.
Плоскость уровня
— плоскости, параллельные плоскостям
проекций – занимают частное положение
в пространстве;
Горизонтальная
плоскость — плоскость, параллельная
горизонтальной плоскости проекций
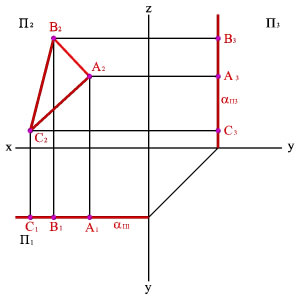
Фронтальная
плоскость — плоскость, параллельная
фронтальной плоскости проекций
Профильная плоскость
— плоскость, параллельная профильной
плоскости проекций

-
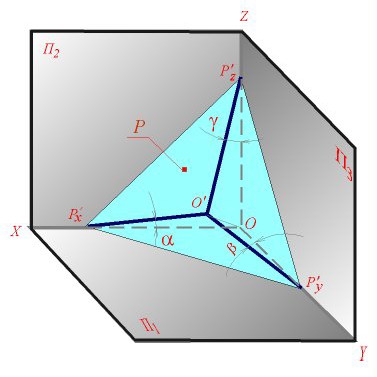
Что называется
следами плоскости и как они изображаются
на эпюре.
Следами плоскости
называются линии пересечения плоскости
с плоскостями проекций.
-
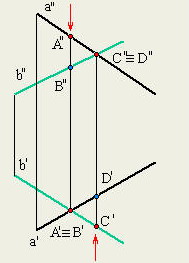
Как определяется
видимость прямой и плоскости по
конкурирующим точкам.
Точки, у которых
проекции на П1
совпадают, называют конкурирующими по
отношению к плоскости П1,
а точки, у которых проекции на П2
совпадают, называют конкурирующими по
отношению к плоскости П2.
-
Как определяется
принадлежности точки плоскости.
Точка принадлежит
плоскости, если она принадлежит прямой,
лежащей в этой плоскости.
-
Как опустить
перпендикуляр из точки к плоскости.
Расстояние от
точки до плоскости равно длине
перпендикуляра, опущенного из точки на
эту плоскость. Пусть требуется найти
расстояние от точки K до плоскости s
(АВС).
Алгоритм построения:
Строится перпендикуляр
из точки K на плоскость s (АВС) : m1 h1, m2
f2.
Находится точка
N — точка пересечения перпендикуляра m
с плоскостью s (АВС).
Определяется
расстояние от точки K до точки N с помощью
прямоугольного треугольника K1N1M0. Длина
гипотенузы N1M0 – это искомое расстояние:
|KN| = N1M0.
-
Как из точки,
принадлежащей плоскости, восстановить
перпендикуляр.
-
Как через точку
провести плоскость, параллельную
заданной плоскости.
-
Когда плоскости
параллельны.
Две плоскости
параллельны, если две пересекающиеся
прямые одной плоскости соответственно
параллельны двум пересекающимся прямым
другой плоскости.
-
В каком случае
плоскости перпендикулярны.
Две плоскости
перпендикулярны, если одна из них
проходит через перпендикуляр к другой.
-
Как изображается
на эпюре точка в проекциях с числовыми
отметками.
Прямоугольные
проекции точек на горизонтальную
плоскость проекций сопровождаемые
числами, определяющими удаление самих
точек от этой плоскости, называются
проекциями с числовыми отметками.
Точка задается
своей горизонтальной проекцией и числом
при ней(отметкой), отражающим высоту
этой точки над горизонтальной плоскостью
проекций.
-
Как изображается
прямая линия в проекциях с числовыми
отметками.
Если взять 2 точки
в пространстве и соединить их прямой,
то получим отрезок, расположенный
определенным образом относительно П0.
Проекция отрезка будет выражена отрезком
А3В5, при наличии линейного масштаба она
вполне определяет отрезок АВ в
пространстве.
-
Что такое уклон
прямой.
Уклон отрезка –
Отношение разности отметок концов к
заложению.
I = hв-hа
/ l = tg(x)
(x-угол наклона прямой к плоскости П0).
-
Что такое интервал
прямой.
Интервалом прямой
называют горизонтальное расстояние
между такими двумя точками прямой,
разность отметок которых равна 1.
L = l / hв-hф.
Если прямая задана
отметками не целых чисел, то для нахождения
точек кратных целому числу проводят
градуирование прямой, то есть находят
отметки чисел, определяют интервал
прямой.
-
Что такое
заложение прямой.
Заложение – это
горизонтальная проекция отрезка прямой
на плоскости нулевого уровня (l).
-
В каком случае
прямые в проекциях с числовыми отметками
параллельны.
Параллельные
прямые могут быть параллельными если
их проекции параллельны, интервалы
равны, уклоны равны, одинаково
ориентированы, отметки возрастают в
одном направлении.
-
В каком случае
прямые в проекциях с числовыми отметками
пересекаются, скрещиваются.
Прямые пересекающиеся
если отметки прямых в точки пересечения
одинаковы, прямые соединяющие точки с
одинаковыми отметками параллельны.
Скрещивающиеся
прямые если отметки в точке пересечения
проекций для каждой прямой разные. Линии
соединяющие точки с одинаковыми отметками
не параллельны. Если проекции скрещивающихся
прямых параллельны, то уклоны должны
быть не равными, или при равных уклонах
противоположно ориентированы.
-
Задание плоскости
в проекциях с числовыми отметками.
а) Тремя точками,
не лежащими на одной прямой, и их
отметками.
б) Прямой и точкой,
не лежащей на этой прямой, и их отметками.
в) Двумя параллельными
прямыми и их отметками.
г) Двумя пересекающимися
прямыми с отметками.
д) Топографической
поверхностью
е) Масштабом уклона
плоскости
-
Что такое масштаб
уклона плоскости.
Масштаб уклона
плоскости – проекция линии наибольшего
наклона (ската), с нанесенными на ней
интервалами.
-
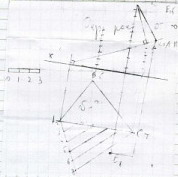
Как опустить
перпендикуляр из точки к плоскости в
проекциях с числовыми отметками.
-
Задание прямой
в проекциях с числовыми отметками.
Проекция прямой
задается:
— двумя точками с
отметками при наличии линейного масштаба;
— точкой с отметкой
и стрелкой с величиной уклона, указывающей
навправление убывания отметок.
-
Как определить
угол простирания плоскости.
Угол простирания
плоскости отсчитывает против часовой
стрелки от северного конца магнитной
стрелки до направления линии простирания
плоскости.
Простиранием
плоскости называется направление
горизонтальной плоскости, указываемое
стрелкой вправо, если смотреть в сторону
возрастания отметок.
-
Как определяется
линия пересечения плоскостей в проекциях
с числовыми отметками, если плоскости
заданы двумя треугольниками.
Градуируем сторону
с наибольшей разностью отметок, проводим
главную линию (соединяем третью вершину
с соответствующей отметкой).
Аналогично со
вторым треугольником.
Ищем точки
пересечения одноименных линий. И получаем
линию пересечения двух треугольников.
-
Как определяется
линия пересечения плоскостей в проекциях
с числовыми отметками, если плоскости
заданы масштабами уклонов.
1.Градуируем
плоскость.
2.Из точек градуировки
проводим перпендикулярные прямые.
3.Одноименные
пересекающиеся прямые, проводим линию
пересечения двух плоскостей.
-
Как определить
точку пересечения прямой общего
положения с плоскостью в ортогональных
проекциях.
Если прямая не
лежит в плоскости и не параллельна ей,
она пересекает плоскость.
Задача на определение
точки пересечения прямой с плоскостью
сводится к следующему:
1) проведению
вспомогательной плоскости (Вспомогательную
плоскость рекомендуется выбирать такую,
которая даст наиболее простое графическое
решение задачи) через данную прямую;
2) нахождению линии
пересечения вспомогательной плоскости
с данной плоскостью;
3) определению
точки пересечения данной прямой с линией
пересечения плоскостей, а следовательно,
с данной плоскостью.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Привет, мой друг, тебе интересно узнать все про определение натуральной величины отрезка прямой линии, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
определение натуральной величины отрезка прямой линии , настоятельно рекомендую прочитать все из категории 7. ИЗОБРАЖЕНИЕ ЛИНИЙ НА ЧЕРТЕЖЕ.
При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.
Рассмотрим пример построения изображения отрезка в истинную величину на комплексном чертеже способом прямоугольного треугольника. Если отрезок расположен параллельно какой-либо из плоскостей проекций, то на эту плоскость он проецируется в натуральную величину. Если же отрезок представлен прямой общего положения, то на одной из плоскостей проекций нельзя определить его истинную величину (см . Об этом говорит сайт https://intellect.icu . рис. 69).
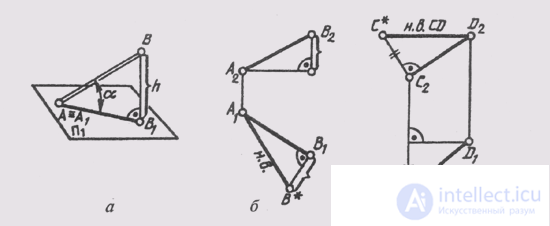
Возьмем отрезок общего положения АВ (A ^ П1) и построим его ортогональную проекцию на горизонтальной плоскости проекций (рис. 78, а). В пространстве при этом образуется прямоугольник А1ВВ1, в котором гипотенузой является сам отрезок, одним катетом — горизонтальная проекция этого отрезка, а вторым катетом — разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек ее отрезка не составляет труда, то можно построить по горизонтальной проекции отрезка (рис. 78, б) прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ.
Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов (рис. 78, в), замеренную на плоскости П1.
Рис. 78
Для определения натуральной величины отрезка прямой можно воспользоваться поворотом ее относительно плоскостей проекций, чтобы она расположилась параллельно одной из них (см. § 36) или вводом новой плоскости проекций (заменой одной из плоскостей проекций) так, чтобы она была параллельна одной из проекций отрезка (см. §§58, 59).
Как ты считаеешь, будет ли теория про определение натуральной величины отрезка прямой линии улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое определение натуральной величины отрезка прямой линии
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
7. ИЗОБРАЖЕНИЕ ЛИНИЙ НА ЧЕРТЕЖЕ
Из статьи мы узнали кратко, но емко про определение натуральной величины отрезка прямой линии
Определение величины
Стандартные метрические задачи начертательной геометрии: определение натуральной величины отрезка прямой
линии, плоской фигуры, плоского или двугранного угла.
Определение натуральной величины отрезка соответствует задаче о расстоянии между двумя точками.
- Натуральная величина
- Определить натуральную величину
- Натуральная величина треугольника
- Натуральная величина плоскости
- Натуральная величина проекции
- Натуральная величина сечения
- Натуральная величина отрезка
- Натуральная величина угла
- Определить натуральную величину треугольника
- Определить натуральную величину плоскости
- Натуральная величина прямой
- Определение натуральной величины
- Определить натуральную величину угла
- Натуральная величина пирамиды
- Построить натуральную величину сечения
- Натуральная величина фигуры
- Построение натуральной величины
- Построить проекции и натуральную величину
- Определить натуральную величину отрезка
- Определить натуральную величину треугольника АВС
- Как находить натуральную величину
- Как найти натуральную величину
- Натуральная величина отрезка прямой
- Определить натуральную величину прямой
- Нахождение натуральной величины
- Определить натуральную величину сечения
- Натуральная величина конуса
- Натуральная величина двугранного угла
- Начертательная геометрия натуральная величина
- Определение натуральной величины отрезка
- Проекция угла натуральная величина
- Натуральная величина треугольника методом вращения
- Определение натуральной величины треугольника
- Натуральная величина призмы
- Натуральная величина сечения конуса
- Определить натуральную величину треугольника ABC
- Определение натуральной величины плоскости
- Натуральная величина фигуры сечения
- Натуральная величина сечения пирамиды
- Натуральная величина треугольника методом замены плоскостей
- Как построить натуральную величину
- Определить натуральную величину фигуры
- Натуральная величина сечения призмы
- Нахождение натуральной величины треугольника
- Определение натуральной величины прямой
- Натуральная величина ребер пирамиды
- Построить натуральную величину треугольника АВС
- Способом замены плоскостей проекций определить натуральную величину
- Построить натуральную величину фигуры
- Построить натуральную величину сечения конуса
- Натуральная величина отрезка прямой общего положения
- Определение натуральной величины отрезка прямой
- Натуральная величина сечения цилиндра
- Определить натуральную величину отрезка АВ
- Как найти натуральную величину треугольника
- Построить натуральную величину отрезка
- Метод прямоугольного треугольника натуральная величина
- Построение натуральной величины сечения
- Определить натуральную величину треугольника методом вращения
- Определить натуральную величину плоской фигуры
- Определение натуральной величины методом вращения
- Определить натуральную величину треугольника методом замены плоскостей
- Способом плоскопараллельного перемещения определить натуральную величину
- Начертательная геометрия натуральная величина треугольника
- Определение натуральной величины плоской фигуры
- Как найти натуральную величину отрезка
- Натуральная величина двугранного угла при ребре
- Определить натуральную величину высоты пирамиды
- Заменой плоскостей проекций определить натуральную величину треугольника
- Определить натуральную величину угла между прямыми
- Определить натуральную величину основания пирамиды
- Построение натуральной величины треугольника
- Натуральная величина отрезка начертательная геометрия
- Определить натуральную величину треугольника АВС методом вращения
- Построить натуральную величину сечения призмы
- Определить натуральную величину треугольника способом плоскопараллельного перемещения
- Натуральная величина параллелограмма
- Определение натуральной величины пирамиды
- Как найти натуральную величину сечения
- Определить натуральную величину угла между плоскостями
- Найти натуральную величину треугольника методом вращения
- Нахождение натуральной величины отрезка
- Прямой угол проецируется в натуральную величину если
- Натуральная величина расстояния от точки до прямой
- Определение натуральной величины сечения
- Определить натуральную величину двугранного угла при ребре
- Как определить натуральную величину двугранного угла
- Натуральная величина треугольника способом вращения
- Натуральная величина треугольника на чертеже
- Натуральная величина треугольника методом плоскопараллельного перемещения
- Определить натуральные величины ребер пирамиды
- Определение натуральной величины треугольника методом вращения
- Плоская фигура проецируется в натуральную величину при
- Натуральная величина отрезка равна
- Определение натуральной величины двугранного угла
- Найти натуральную величину треугольника методом замены плоскостей
- Как найти натуральную величину пирамиды
- Нахождение натуральной величины сечения
- Натуральная величина сечения усеченной призмы
- Построить проекции и натуральную величину линии сечения
- Вращением вокруг горизонтали определить натуральную величину треугольника
- Определение натуральной величины отрезка прямой общего положения
- Определить натуральную величину сечения конуса плоскостью
- Определить натуральную величину сечения пирамиды плоскостью
- Построение натуральной величины отрезка
- Натуральная величина угла между прямой и плоскостью
- Как найти натуральную величину треугольника начертательная геометрия
- Натуральная величина сечения сферы
- Определение натуральной величины методом прямоугольного треугольника
- Способом прямоугольного треугольника определить натуральную величину
- Натуральная величина отрезка равна гипотенузе прямоугольного треугольника
- Определить натуральную величину основания АВС
- Методом прямоугольного треугольника определить натуральную величину
- Определить натуральную величину отрезка ab
- Как построить натуральную величину треугольника
- Найти натуральную величину треугольника АВС
- Способы определения натуральной величины треугольника на чертеже
- Определить натуральную величину параллелограмма
- Определение натуральной величины отрезка и углов наклона
- Определить натуральную величину отрезка методом вращения
- Определение натуральной величины способ вращения
- Построение натуральной величины фигуры сечения
- Найти натуральную величину угла АВС
- Когда ребро детали проецируется в натуральную величину
- Нахождение натуральной величины методом прямоугольного треугольника
- Определить натуральную величину угла между пересекающимися прямыми
- Найти натуральную величину двугранного угла
- Как найти натуральную величину прямой
- Определение натуральной величины отрезка методом треугольника
- Натуральная величина сечения усеченной пирамиды
- Определить натуральную величину треугольника АВС решение
- Построение натуральной величины треугольника методом замены плоскостей
- Определить натуральную величину отрезка методом прямоугольного треугольника
- Начертательная геометрия определение натуральной величины отрезка
- Определить методом замены плоскостей натуральную величину сечения
- Определить натуральную величину плоской фигуры способом вращения
- Определить натуральную величину трапеции
- На чертеже решена задача нахождения натуральной величины
- Определить натуральную величину треугольника АВС способом вращения
- Как построить натуральную величину сечения пирамиды плоскостью
- Натуральную величину отрезка прямой способом прямоугольного треугольника
- Найти натуральную величину фигуры методом вращения
- Как найти натуральную величину цилиндра
- Определить натуральную величину четырехугольника abcd
- Как строить натуральную величину сечения
- Нахождения натуральной величины по правилу прямоугольного треугольника
- Нахождение натуральной величины треугольника методом вращения
- Нахождение натуральной величины отрезка методом прямоугольного треугольника
- Нахождение натуральной величины отрезка общего положения
- Определение натуральной величины отрезка метод прямоугольного треугольника
- Как построить натуральную величину сечения цилиндра
- Определение натуральной величины высоты пирамиды
- Как определить натуральную величину прямой общего положения
- Натуральную величину отрезка АВ можно найти методом
- Найти натуральную величину угла между скрещивающимися прямыми
- Как найти натуральную величину сечения цилиндра
- Построить натуральную величину сечения заданной фигуры плоскостью
- Определить натуральную величину перпендикуляра к плоскости треугольника
- Определение натуральной величины отрезка прямой начертательная геометрия
- Как найти натуральную величину сечения пирамиды
- Нахождение натуральной величины треугольника методом замены плоскостей
- Натуральная величина сечения призмы с продольным отверстием
- Определить натуральную величину высоты пирамиды в начертательной геометрии
- Натуральная величина сечения усеченной призмы определена способом
- Найти натуральную величину отрезка методом прямоугольного треугольника
- Определить натуральную величину угла начертательная геометрия
- Определить натуральную величину трапеции abcd
- Как найти натуральную величину высоты пирамиды
- Построение натуральной величины сечения конуса
- Угол равный натуральной величине
- Определить натуральную величину треугольника АБС
- Определение натуральной величины отрезка способом прямоугольного треугольника
- Почему очерковая образующая конуса в натуральную величину
- Построение натуральной величины треугольника методом вращения
- Определить натуральную величину шара методом замены плоскостей
- Определить натуральную величину параллелограмма методом вращения
- Определить натуральную величину высоты SO пирамиды SABC
- Определение натуральной величины отрезка методом совмещения
- Истинная величина
- Истинное значение величины
- Определить истинную величину
- Найдите истинную величину
- Истинная величина треугольника
- Истинная величина плоскости
- Истинная величина отрезка
- Определить истинную величину угла
- Определение истинной величины
- Найти истинную величину треугольника
- Истинная величина сечения
- Определить истинную величину треугольника
- Истинная величина двугранного угла
- Истинное и действительное значение величины
- Определить истинную величину расстояния
- Определить истинную величину отрезка
- Определить истинную величину двугранного угла
- Истинная величина плоской фигуры
- Определить истинную величину угла между прямыми
- Определение истинной величины треугольника
- Определить истинную величину отрезка АВ
- Определить истинную величину двугранного угла при ребре
- Определить истинную величину плоской фигуры
- Определение истинной величины сечения
- Найти истинную величину отрезка
- Определить истинную величину двугранного угла начертательная геометрия
- Определить истинную величину треугольника ABC
- Определить истинную величину основания ABC
- Определить истинную величину грани SAC
- Определить истинную величину угла между пересекающимися прямыми
- Определение истинной величины отрезка
- Дан четырехгранник ABCD определить истинную величину
- Как построить истинную величину сечения
- Нахождение истинной величины отрезка
- Определение истинной величины сечения пирамиды
Решение задач по начертательной геометрии.
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩