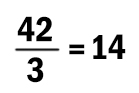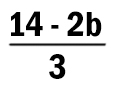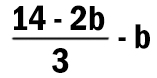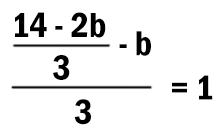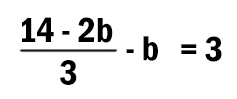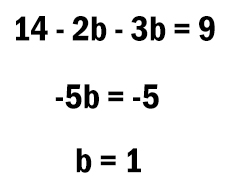Как найти натуральное число в информатике - AvtoShod.ru

Раздел:
Задачи /
Простейшие /

Проверка натурального числа

Основы программирования
Каждый профессионал когда-то был чайником. Наверняка вам знакомо состояние, когда “не знаешь как начать думать, чтобы до такого додуматься”. Наверняка вы сталкивались с ситуацией, когда вы просто не знаете, с чего начать.
Эта книга ориентирована как раз на таких людей, кто хотел бы стать программистом, но совершенно не знает, как начать этот путь.
Подробнее…

Условие задачи 1.1

Задача 1.1
Дано число Х. Если оно натуральное, то вывести на экран сообщение: “Х — натуральное число”, иначе — вывести сообщение “Х — действительное число”.

Прежде чем начать решать эту задачу, давайте вспомним, что такое натуральные и действительные числа.

Что такое натуральное число

Натуральные числа (от лат. naturalis — естественный; естественные числа) — это числа, возникающие естественным образом при счёте (например, 1, 2, 3). Последовательность всех натуральных чисел, расположенных в порядке возрастания, называется натуральным рядом.

Существуют два подхода к определению натуральных чисел:

Натуральные числа — это числа, возникающие при подсчёте (нумерации) предметов (первый, второй, третий и т.д.).
Натуральные числа — это числа, возникающие при обозначении количества предметов (нет предметов, один предмет, два предмета и т.д).

В первом случае ряд натуральных чисел начинается с единицы, а во втором — с нуля.

Отрицательные и нецелые (рациональные, вещественные, …) числа к натуральным не относятся.

Что такое действительное число

Вещественное, или действительное число (от лат. realis — действительный) — это математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений, исследование поведения функций.

Если натуральные числа возникли в процессе счёта, а рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин.

Не будем углубляться в теорию. Попробуем подвести итог простыми словами. Итак,

Натуральное число — это целое положительное число.

Вещественное (действительное) число — это не целое число (число с дробной частью).

Теперь попробуем найти решение задачи. Вариантов может быть несколько. Мы попробуем два из них — проверку натурального числа и проверку действительного числа. Они мало чем отличаются, но всё же.

Чтобы как-то отличить их, оформим их в виде функций.

Как проверить натуральное число

Можно выбрать, например, такой алгоритм:

Получить число Х
Проверить, не является ли число отрицательным
Если да, то вывести “Х — действительное число”
Если нет, то

Выделить дробную часть числа
Если она равна нулю, то вывести “Х — натуральное число”
Иначе вывести “Х — действительное число”

Завершить программу

Поскольку мы решили оформить решения в виде функций, то проверка натурального числа поместится в одну строку исходного кода.

//*********************************************************
// Проверяет, является ли число натуральным.
// ВХОД: проверяемое число
// ВЫХОД: TRUE - число является натуральным, 
// FALSE - не является
//*********************************************************
function NumIsNatural(N : Single) : boolean;
begin
  Result := (N >= 0) and (Frac(N) = 0);
end;

Проверка действительного числа

Как я уже говорил, такая проверка мало чем отличается от предыдущей и также помещается в одну строку исходного кода:

//*********************************************************
// Проверяет, является ли число действительным (вещественным)
// ВХОД: проверяемое число
// ВЫХОД: TRUE - число является действительным, 
//        FALSE - не является
//*********************************************************
function NumIsReal(N : Single) : boolean;
begin
  Result := (N < 0) or (Frac(N) > 0);
end;

Ниже приведены примеры программ на языках Паскаль и
С++.

Решение задачи 1.1 на Паскале

program natural;

var X : Single;
    N : Single;

//****************************************************************
// Проверяет, является ли число натуральным.
// ВХОД: проверяемое число
// ВЫХОД: TRUE - число является натуральным, FALSE - не является
//****************************************************************
function NumIsNatural(N : Single) : boolean;
begin
  Result := (N >= 0) and (Frac(N) = 0);
end;

//****************************************************************
// Проверяет, является ли число действительным (вещественным).
// ВХОД: проверяемое число
// ВЫХОД: TRUE - число является действительным, 
// FALSE - не является
//****************************************************************
function NumIsReal(N : Single) : boolean;
begin
  Result := (N < 0) or (Frac(N) > 0);
end;

//****************************************************************
// ОСНОВНАЯ ПРОГРАММА
//****************************************************************
begin
  //Проверка натурального числа
  Write('X = ');
  ReadLn(X);
  if NumIsNatural(X) then
    WriteLn('X is a natural number')
  else
    WriteLn('X is a real number');

  //Проверка действительного числа
  Write('X = ');
  ReadLn(X);
  if NumIsReal(X) then
    WriteLn('X is a real number')
  else
    WriteLn('X is a natural number');

  ReadLn;
end.

Решение задачи 1.1 на С++

#include 
#include 

using namespace std;

//****************************************************************
// Проверяет, является ли число натуральным.
// ВХОД: проверяемое число
// ВЫХОД: TRUE - число является натуральным, FALSE - не является
//****************************************************************
bool NumIsNatural(float N)
{
  int a = (int)N;
  return ((N >= 0) && ((N - a) == 0));
}

//****************************************************************
// Проверяет, является ли число действительным (вещественным).
// ВХОД: проверяемое число
// ВЫХОД: TRUE - число является действительным, 
// FALSE - не является
//****************************************************************
bool NumIsReal(float N)
{
  int a = (int)N;
  return ((N < 0) || ((N - a) != 0));
} 

//****************************************************************
// ОСНОВНАЯ ПРОГРАММА
//****************************************************************
int main(int argc, char *argv[])
{
  float X;
  //Проверка натурального числа
  cout << "X = ";
  cin >> X;
  if (NumIsNatural(X)) 
    cout << "X is a natural number" << endl;
  else
    cout << "X is a real number" << endl;

  //Проверка действительного числа
  cout << "X = ";
  cin >> X;
  if (NumIsReal(X)) 
    cout << "X is a real number" << endl;
  else
    cout << "X is a natural number" << endl;

  system("PAUSE");
  return EXIT_SUCCESS;
}

ВАЖНО!
Из-за особенностей представления вещественных чисел в памяти компьютера эти примеры не будут работать с большими числами. Например, эти функции, скорее всего, определят, что число 567894,01 является натуральным, а число 567894,1 — действительным. Числа с меньшими значениями будут определяться более точно. Например, число 1,0000001 (шесть нулей) определится как вещественное, а число 1,00000001 (семь нулей) определится как натуральное.

Можно, конечно, постараться и сделать работу этих функций более точной. Но это уже будет более сложное решение.

Как стать программистом 2.0

Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки…
Подробнее…

Помощь в технических вопросах

Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации.
Подробнее…

Источник

Урок посвящен тому, как решать 5 задание ЕГЭ по информатике

Содержание:

Объяснение 5 задания
- Исполнитель для возведения в квадрат, деления, умножения и сложения
- Проверка числовой последовательности на соответствие алгоритму
Разбор 5 задания
- Решение задания про алгоритм, который строит число R
- Решение заданий для темы Проверка числовой последовательности (Автомат)

5-е задание: «Анализ алгоритмов и исполнители»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 4 минуты.

Проверяемые элементы содержания: Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд

До ЕГЭ 2021 года — это было задание № 6 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Как и в других заданиях базового уровня сложности, источником ошибок служит недостаточная внимательность и отсутствие или поверхностность самостоятельной проверки полученного ответа»

ФГБНУ «Федеральный институт педагогических измерений»

Проверка числовой последовательности на соответствие алгоритму

для выполнения некоторых заданий необходимо повторить тему системы счисления;
максимальное значение суммы цифр десятичного числа — это 18, так как 9 + 9 = 18;
для проверки правильности переданного сообщения иногда вводится бит четности — дополнительный бит, которым дополняется двоичный код таким образом, чтобы в результате количество единиц стало четным: т.е. если в исходном сообщении количество единиц было четным, то добавляется 0, если нечетным — добавляется 1:

например: 
 3₁₀ = 11₂ 
после добавления бита четности: 110
----
 4₁₀ = 100₂ 
после добавления бита четности: 1001

добавление к двоичной записи числа нуль справа увеличивает число в 2 раза:

например:
111₂ - это 7₁₀
добавим 0 справа:
1110₂ - это 14₁₀

Теперь будем рассматривать конкретные типовые экзаменационные варианты по информатике с объяснением их решения.

Разбор 5 задания

Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:

Решение задания про алгоритм, который строит число R

5_11:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

Строится двоичная запись числа 4N.
К этой записи дописываются справа еще два разряда по следующему правилу:

складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись является двоичной записью искомого числа R.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 129. В ответе это число запишите в десятичной системе счисления.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

Заметим, что после выполнения второго пункта задания, будут получаться только четные числа! Наименьшим возможным четным числом, превышающим 129, является число 130. С ним и будем работать.
Переведем 130 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(130). Получим:

130₁₀ = 10000010₂

Это двоичное число получилось из исходного двоичного, после того как дважды был добавлен остаток от деления суммы цифр на 2. Т.е.:

в обратном порядке:
было 1000001 -> стало 10000010 
еще раз то же самое: 
было 100000 -> стало 1000001

Значит, необходимое нам двоичное число — это 100000.
Переведем 100000 в 10-ю систему. Для этого можно воспользоваться калькулятором, либо использовать интерпретатор Питона: int('100000',2).

100000₂ = 32₁₀

Так как по условию у нас 4*N, то 32 делим на 4 — > 8.

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := 4*n_;
    var ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряру (+ost)
    ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost;
    if n > 129 then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = 4*n_
    r = str(bin(n))
    r = r[2:]
    for i in range(2):
        if r.count('1') % 2 == 0:
            r+='0'
        else:
            r+='1'
 
    n = int(r, base=2)
    if n > 129:
        print(n_)
        break
    n_+=1

Результат: 8

Для более детального разбора предлагаем посмотреть видео теоретического решения данного 5 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_12: Демоверсия ЕГЭ 2018 информатика:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

Строится двоичная запись числа N.
К этой записи дописываются справа ещё два разряда по следующему правилу:
складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
Наименьшим возможным числом, превышающим 83, является число 84. С ним и будем работать.
Переведем 84 в двоичную систему счисления. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(84). Получим:

84 = 1010100

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так как оно нечетное. А мы имеем 0. Соответственно, это оно не подходит.
Возьмем следующее четное число — 86. Переведем его в двоичную систему счисления:

86 = 1010110

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так и есть: 101011. А затем добавляется 0: 1010110. Соответственно, оно подходит.

Результат: 86

Подробное решение данного 5 (раньше №6) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Видеорешение с программированием (PascalAnc.Net):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Аналитическое видеорешение:

📹 Видеорешение на RuTube здесь -> аналитическое решение

5_18:

Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3. Шаг 2 повторяется ещё два раза.
4. Результат переводится в десятичную систему счисления.

При каком наименьшем исходном числе N > 65 в результате работы алгоритма получится число, кратное 4?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
    for var i := 1 to 3 do 
    begin
      if bin(n).CountOf('1') = bin(n).CountOf('0') then // сравниваем
        if n mod 2 = 0 then // если четное, то в конце 0
          n := 2 * n  // добавляем разряд = 0
        else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
      else if bin(n).CountOf('1') > bin(n).CountOf('0') then
        n := 2 * n
      else
        n := 2 * n + 1
    end;
    if (n_ > 65) and (n mod 4 = 0) then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(3):
        if r.count('1') == r.count('0'):
            r+=r[-1] 
        elif r.count('1')>r.count('0'):
            r+='0'
        else:
            r+='1'
    n = int(r, base=2)
    if n_ > 65 and n % 4 == 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 79

5_19:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Число N переводим в двоичную запись.
2) Инвертируем все биты числа кроме первого.
3) Переводим в десятичную запись.
4) Складываем результат с исходным числом N.
Полученное число является искомым числом R.

Укажите наименьшее нечетное число N, для которого результат работы данного алгоритма больше 99. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(1,len(r)):
        if r[i]== '0':
            r=r[:i]+'1'+r[i+1:] 
        else:
            r=r[:i]+'0'+r[i+1:] 
    n = int(r, base=2)
    n+=n_
    if n > 99 and n_ % 2 != 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 65

5_13:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописываются справа еще два разряда по следующему правилу:
— если N делится нацело на 4, в конец числа (справа) дописывается сначала ноль, а затем еще один ноль;
— если N при делении на 4 дает в остатке 1, то в конец числа (справа) дописывается сначала ноль, а затем единица;
— если N при делении на 4 дает в остатке 2, то в конец числа (справа) дописывается сначала один, а затем ноль;
— если N при делении на 4 дает в остатке 3, в конец числа (справа) дописывается сначала один, а затем еще одна единица.

Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.

Укажите максимальное число R, которое меньше 100 и может являться результатом работы данного алгоритма. В ответе это число запишите

в десятичной системе счисления

Типовые задания для тренировки

✍ Решение:

Поскольку требуется найти наибольшее число, то возьмем наибольшее из возможных чисел, которые < 100 — это число 99. Переведем его в двоичную систему. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(99). Получим:

99 = 1100011₂

По алгоритму это число получилось путем добавления справа двух разрядов, значение которых зависит от исходного N:

1100011
  N

Т.е. в конце были добавлены две единицы — по алгоритму это значит, что исходное N должно в остатке при делении на 4 давать 3. Переведем найденное N в десятичную систему. Можно использовать калькулятор либо консоль пайтон: int('11000',2)

11000 = 24₁₀

24 делится на 4 нацело, т.е. в конце по алгоритму должны были добавиться два разряда — 00. У нас же в конце 11. Т.е. число 99 не подходит. Проверим следующее — 98.

98 = 1100010₂  : 10 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 10 
98 - не подходит

97 = 1100001₂ : 01 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 01 
97 - не подходит

96 = 1100000₂ : 00 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, у нас 00 - верно!
96 - подходит!

Результат: 96

Предлагаем посмотреть видео теоретического решения:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_14:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописывается (дублируется) последняя цифра.
3. Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4. К полученному результату дописывается ещё один бит чётности.

Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, большее 114, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

В постановке задания задано R > 114. R — это результат работы алгоритма. Для того, чтобы определить наименьшее возможно N, переведем сначала 114 в двоичную систему счисления и выделим в нем три добавленные по алгоритму цифры (перевод можно выполнить в консоли Питона: bin(114))

114 = 1110010₂

Проанализируем, как могло бы получиться двоичное число 114 (R) по алгоритму:

2. В полученное числе N = 1110 дублируется последняя цифра и получается 11100.
3. Поскольку число единиц (3) — нечетное, то справа добавляется 1: 111001.
4. Т.к. в полученном наборе цифр четное число единиц, то добавляем 0: 1110010

Поскольку из числа N = 1110 по алгоритму могла получиться только такая последовательность цифр (1110010), то для получения минимального R, но большего чем R = 114, увеличим в N = 1110 самый младший разряд на единицу и рассмотрим работу алгоритма с полученным числом:

1. N = 1110 + 1 = 1111

Работа по алгоритму:
2. 11111 - дублирование последней цифры.
3. 111111 - справа дописываем единицу, т.к. в полученном числе 5 единиц (нечетное)
4. 1111110 - дописываем ноль, т.к. в полученном числе четное число единиц.

Ответ нужно получить в десятичной системе счисления (для перевода можно воспользоваться интерпретатором Питона: int('1111110',2)):

min R = 1111110₂ = 126₁₀

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
          // дублирвание последней цифры
    if n mod 2 = 0 then // если четное, то в конце 0
      n := 2 * n  // добавляем разряд = 0
    else 
      n := 2 * n + 1; // иначе добавляем разряд = 1
    for var i := 1 to 2 do
    begin
      if bin(n).CountOf('1') mod 2 = 0 then
        n := 2 * n  // добавляем разряд = 0
     else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
    end;
    if n > 114 then
    begin
      println(n);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r  = str(bin(n)) # строковое значение
    r = r[2:] # убираем 0b
    r=r+r[-1]
    for i in range (2):
        if r.count('1') % 2 == 0:
            r = r+'0'
        else:
            r = r+'1'
    r = int(r,base = 2) # в 10-ю с.с.
    if r > 114:
        print(r)
        break
    n_+= 1

Результат: 126

5_17: Досрочный вариант 1 ЕГЭ по информатике 2020, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
— если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы.

Например, двоичная запись 1001 числа 9 будет преобразована в 100111.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.

Укажите минимальное число N, для которого результат работы алгоритма будет больше 134. В ответе это число запишите в десятичной системе счисления.

Ответ: 33

Видео -> теоретическое решение
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_16:

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:

1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из нового числа вычитается исходное, полученная разность выводится на экран.

Какое число нужно ввести в автомат, чтобы в результате получилось 45?

✍ Решение:

Результатом выполнения алгоритма является число 45. Алгоритм работает в двоичной системе счисления, поэтому переведем число:

45 = 00101101₂

Пронумеруем биты слева направо, начиная с единицы. Рассмотрим каждый бит отдельно, начиная с левого бита под номером 1.
1. Так как биты в уменьшаемом и вычитаемом должны быть различны, то единица в результате может получится только 1 - 0, с учетом, что у разряда с единицей заняли. То есть бит:

   .
_{_}  1 _ _ _ _ _ _ _    N инвертируемое
₌  0 _ _ _ _ _ _ _    N исходное
   0 0 1 0 1 1 0 1  = 45   результат

2. 1 - 0 не может в результате дать 0, так как у следующей слева единицы мы заняли. Значит, 0 - 1. Чтобы не получить единицу в ответе, необходимо у нуля тоже занять:

   . .
_{_}  1 0 _ _ _ _ _ _ 
₌  0 1 _ _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

3. 1 - 0 не может быть, так как у следующего слева нуля мы заняли.
Значит 0 - 1. То есть как раз чтобы получить единицу (10 - 1 = 1), занимаем у следующих слева разрядов:

   . .
_{_}  1 0 0 _ _ _ _ _ 
₌  0 1 1 _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

4. 0 - 1 не может быть. Значит, чтобы получить в результате ноль, берем 1 - 0, у единицы должно быть занято.

   . .   .
_{_}  1 0 0 1 _ _ _ _ 
₌  0 1 1 0 _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

5. 1 - 0 не может быть. Так как слева у единицы занято. Значит, чтобы получить в результате 1, берем 0 - 1:

   . .   .
_{_}  1 0 0 1 0 _ _ _ 
₌  0 1 1 0 1 _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

6. 0 - 1 не даст в ответе единицу, значит, имеем 1 - 0:

   . .   .
_{_}  1 0 0 1 0 1 _ _ 
₌  0 1 1 0 1 0 _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

7. 0 - 1 не может быть, значит, 1 - 0. Чтобы получить в результате 0, необходимо, чтобы у 1 было занято:

   . .   .     .
_{_}  1 0 0 1 0 1 1 _ 
₌  0 1 1 0 1 0 0 _ 
   0 0 1 0 1 1 0 1  = 45   результат

8. Чтобы получить 1, имеем 0 - 1:

   . .   .     .
_{_}  1 0 0 1 0 1 1 0 
₌  0 1 1 0 1 0 0 1
   0 0 1 0 1 1 0 1  = 45   результат

Полученное число (вычитаемое) и есть искомое N. Переведем его в 10-ю с.с.:

01101001 = 105₁₀

Ответ: 105

Смотрите теоретический разбор задания на видео и подписывайтесь на наш канал:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

Решение заданий для темы Проверка числовой последовательности (Автомат)

5_7:

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.

Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.

Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.

✍ Решение:

Результат: 2949

Процесс теоретического решения данного 5 задания представлен в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_8:

Автомат получает на вход четырехзначное число. По нему строится новое число по следующим правилам:

Складываются первая и вторая, затем вторая и третья, а далее третья и четвёртая цифры исходного числа.
Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).

Пример: Исходное число: 7531. Суммы: 7+5=12; 5+3=8; 3+1=4. Результат: 4812.

✍ Решение:

Число 2512 можно разбить на 2, 5, 12

Начнем с 12. Необходимо получить наибольшее число, поэтому разобьем на слагаемые с наибольшей цифрой — 9:

12=9+3

То есть первые две цифры:

 93**

В число 2 тройка не входит, значит забираем тройку из 5. Остается 2. А, значит, из состава 2 остается 0.

Получим число: 9320.

Результат: 9320

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_9:

Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам:

Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
Полученные два шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).

Пример: Исходные числа: 25, 66. Поразрядные суммы: 8, B. Результат: B8.

Какие из предложенных чисел могут быть результатом работы автомата?
Перечислите в алфавитном порядке буквы, соответствующие этим числам, без пробелов и знаков препинания.

Варианты:
A) 127
B) C6
C) BA
D) E3
E) D1

✍ Решение:

Проанализируем все варианты:

Вариант А. 127 не подходит, так как число 12 в шестнадцатеричной системе записывается как С.

Вариант В. С6 разбиваем на 12 и 6. Число может быть результатом работы автомата. Исходные числа, например, 35 и 37

Вариант С. BA разбиваем на 11 и 10. Число может быть результатом работы автомата. Исходные числа, например, 55 и 56

Вариант D. E3 разбиваем на 14 и 3. 14=6+8, но цифры большие 6 не принимает автомат. Не подходит.

Вариант E. D1 разбиваем на 13 и 1. 13=6+7, но цифры большие 6 не принимает автомат. Не подходит.

Результат: BC

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_10: Задание 5 ГВЭ 11 класс 2018 год ФИПИ

Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 7 (если в числе есть цифра больше 7, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.

1. Вычисляются два шестнадцатеричных числа: сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.

Определите, какое из предложенных чисел может быть результатом работы автомата.

Варианты:
1) AD
2) 64
3) CF
4) 811

✍ Решение:

Теоретическое решение 4 задания ГВЭ 11 класса смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_15:

Автомат получает на вход натуральное число X. По этому числу строится трёхзначное число Y по следующим правилам:
1. Первая цифра числа Y (разряд сотен) – остаток от деления X на 7.
2. Вторая цифра числа Y (разряд десятков) – остаток от деления X на 2.
3. Третья цифра числа Y (разряд единиц) – остаток от деления X на 5.

Пример. Исходное число: 55. Остаток от деления на 7 равен 6; остаток от деления на 2 равен 1; остаток от деления на 5 равен 0. Результат работы автомата: 610.

Сколько существует двузначных чисел, при обработке которого автомат выдаёт результат 312?

Типовые задания для тренировки

✍ Решение:

Обозначим каждую цифру числа Y согласно заданию:

Y =    3       1       2
^{x mod 7    x mod 2    x mod 5}

Сделаем выводы:

1. x mod 2 = 1 => значит, X — нечетное число
2. x mod 5 = 2 => значит, X — либо ?2, либо ?7.
3. раз x — нечетное, то из пред. пункта получаем x = ?7
4. x mod 7 = 3 => переберем все варианты:

97 - не подходит, 
87 - подходит (87 / 7 = 12, остаток = 3)
77 - не подходит,
67 - не подходит,
57 - не подходит,
47 - не подходит,
37 - не подходит,
27 - не подходит,
17 - подходит (17 / 7 = 2, остаток = 3)

Результат: 2

Источник

Сегодня изучим 5 задание из ОГЭ по информатике 2023. Это задание понятное и несложное.

Обычно в 5 задании из ОГЭ по информатике даются команды, которые может делать исполнитель, и зная начальное и конечное положение, нужно найти какой-нибудь параметр одной из команд.

Лучше один раз решить, чем сто раз услышать, приступим к первой тренировочной задаче.

Задача (Составляем программу)

У исполнителя Вычислитель две команды, которым присвоены номера:

приписать 1
разделить на 3

Первая из них приписывает к числу справа 1, вторая уменьшает его в три раза.

Составьте алгоритм получения из 5 числа 19, содержащий не более 5 команд. В ответе запишите только номера команд.

(Например, 22121 — это алгоритм
разделить на 3
разделить на 3
приписать 1
разделить на 3
приписать 1,
который преобразует число 18 в 71.)

Если таких алгоритмов более одного, запишите любой из них.

Решение:

Нам нужно получить из 5 число 19, используя только две вышеуказанные команды. Здесь нужно пробовать составить команды, опираясь на интуицию и здравый смысл. Важно знать, что решение точно есть! Следим за тем, чтобы длина алгоритма не превышала 5 команд.

5 → 51 (Команда 1)
51 : 3 = 17 (Команда 2)
17 → 171 (Команда 1)
171 : 3 = 57 (Команда 2)
57 : 3 = 27 (Команда 2)

Ответ: 12122

Задача (Составляем программу, закрепление)

У исполнителя Квадратор две команды, которым присвоены номера:

возведи в квадрат
вычти 3

Первая из них возводит число на экране во вторую степень, вторая вычитает из числа 3.

Исполнитель работает только с натуральными числами.

Составьте алгоритм получения из числа 14 числа 58, содержащий не более 5 команд. В ответе запишите только номера команд.

(Например, 21221 — это алгоритм
вычти 3
возведи в квадрат
вычти 3
вычти 3
возведи в квадрат
который преобразует число 7 в 100.)

Если таких алгоритмов более одного, запишите любой из них.

Решение:

Здесь, скорее всего, нужно добраться до 64. Потом два раза сделать -3, получится 58.

14 — 3 = 11 (Команда 2)
11 — 3 = 8 (Команда 2)
8² = 64 (Команда 1)
64 — 3 = 61 (Команда 2)
61 — 3 = 58 (Команда 2)

Ответ: 22122

Задача (Составляем программу, ещё раз)

У исполнителя Квадратор две команды, которым присвоены номера:

возведи в квадрат
прибавь 2

Первая из них возводит число на экране во вторую степень, вторая прибавляет к числу 2.

Составьте алгоритм получения из числа 1 числа 85, содержащий не более 5 команд. В ответе запишите только номера команд.

(Например, 21221 — это алгоритм
прибавь 2
возведи в квадрат
прибавь 2
прибавь 2
возведи в квадрат
который преобразует число 1 в 169.)

Если таких алгоритмов более одного, запишите любой из них.

Решение:

Здесь, скорее всего, нужно добраться до 81. Потом два раза прибавить 2, получится 85.

1 + 2 = 3 (Команда 2)
3² = 9 (Команда 1)
9² = 81 (Команда 1)
81 + 2 = 83 (Команда 2)
83 + 2 = 85 (Команда 2)

Ответ: 21122

Задача (Стандартная)

У исполнителя Гамма две команды, которым присвоены номера:

1. прибавь 3;
2. умножь на b
(b  — неизвестное натуральное число; b ≥ 2).

Выполняя первую из них, Гамма увеличивает число на экране на 3, а выполняя вторую, умножает это число на b. Программа для исполнителя Гамма  — это последовательность номеров команд. Известно, что программа 11121 переводит число 3 в число 75. Определите значение b.

Решение:

В начале у нас есть число 3. С ним начинаем делать команды из программы (11121).

Сперва нужно выполнить три раза команду 1.

3 + 3 = 6
6 + 3 = 9
9 + 3 = 12

В 5 задании из ОГЭ по информатике важно знать: мы делаем очередную команду к предыдущему результату.

Следуя программе, дальше нужно сделать команду под номером 2. Получается 12 * b. Затем выполним последнюю команду под номером 1. В результате будет выражение 12 * b + 3. Это выражение в итоге должно равняться 75.

12 * b + 3 = 75

Теперь осталось решить уравнение и найти b.

12 * b = 72
b = 6

В ответе напишем 6.

Ответ: 6

Задача (С делением)

У исполнителя Омега две команды, которым присвоены номера:

1. прибавь 3;
2. раздели на b
(b  — неизвестное натуральное число; b ≥ 2).

Выполняя первую из них, Омега увеличивает число на экране на 3, а выполняя вторую, делит это число на b. Программа для исполнителя Омега  — это последовательность номеров команд. Известно, что программа 11121 переводит число 30 в число 6. Определите значение b.

Решение:

К первоначальному числу 30 применим три раза команду под номером 1.

30 + 3 = 33
33 + 3 = 36
36 + 3 = 39

Затем применим вторую команду. Получается 39 / b. Последней командой будет снова команда под номером один 39 / b + 3. Результат должен быть равен 6.

39 / b + 3 = 6

Решим это уравнение.

39 / b = 3
b = 39 / 3 = 13

Получаем b = 13.

Ответ: 13

Задача (Квадратное уравнение)

У исполнителя Алго две команды, которым присвоены номера:

1. прибавить 1
2. умножить на b
(b — неизвестное натуральное число; b ≥ 2)

Выполняя первую из них, Алго — это последовательность команд.

Известно, что программа 12121 переводит число 4 в число 49.

Определите значение b.

Решение:

Сделаем команды из программы для первоначального числа 4.

4 + 1 = 5
5b
5b+1
(5b+1)*b = 5b² + b
5b² + b + 1

Конечный результат должен равняться 49.

5b² + b + 1 = 49

Получили квадратное уравнение!

5b² + b — 48 = 0
D = 1 + 4 * 5 * 48 = 961

Иногда без калькулятора бывает трудно определить, какое число нужно возвести в квадрат, чтобы получить дискриминант. В этом случае нужно посмотреть на последнюю цифру. У нас это 1. Какое число при возведении в квадрат получает на конце единицу ? Это 1 и 9. Значит, на эти цифры может оканчиваться искомое число. Чтобы подобраться к числу 900, можно попробовать возвести 31 в квадрат. Проверив столбиком число 31, подтверждаем, что 31 это и есть корень из дискриминанта.

b=(-1 + 31) / (2 * 5) = 3

Второй корень получается отрицательный, он нам не подходит.

Ответ: 3

Задача(Двухэтажная дробь)

У исполнителя Омега две команды, которым присвоены номера:

1. вычти b
2. раздели на 3
(b  — неизвестное натуральное число).

Выполняя первую из них, Омега уменьшает число на экране на b, а выполняя вторую, делит это число на 3.

Программа для исполнителя Омега — это последовательность номеров команд.

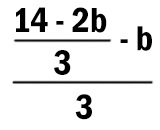
Известно, что программа 211212 переводит число 42 в число 1.

Определите значение b.

Решение:

Выполним команду под номером 2 с первоначальным числом 42.

Далее нужно сделать два раза команду под номером 1.

Далее идёт команда под номером 2.

Ещё раз команду 1.

Выполним последний раз команду под номером 2.

Это выражение после выполнения программы должно равняться 1. Получаем уравнение, которое нужно решить.

Ответ: 1

Задача (Возведение в квадрат)

У исполнителя Омега две команды, которым присвоены номера:

1. прибавь b
2. возведи в квадрат
(b — неизвестное натуральное число).

Выполняя первую из них, Омега увеличивает число на экране на b, а выполняя вторую, заменяет число на экране на это же число, возведённое в квадрат.

Программа для исполнителя Омега — это последовательность номеров команд.

Известно, что программа 11112 переводит число 2 в число 100.

Определить значение b.

Решение:

Начнём делать с первоначальном числом 2 все команды из программы.

2 + b
2 + b + b = 2 + 2b
2 + 2b + b = 2 + 3b
2 + 3b + b = 2 + 4b

Мы сделали первые четыре команды из программы. Получили 2 + 4b. Теперь применим последнюю команду возведение в квадрат. В итоге получаем (2 + 4b)². Это выражение должно равняться числу 100. Получается уравнение.

(2 + 4b)² = 100

Здесь можно применить формулу квадрата суммы, тогда получится квадратное уравнение, но мы воспользуемся формулой разностью квадратов!

(2 + 4b)² — 100 = 0
(2 + 4b — 10)*(2 + 4b + 10) = 0
2 + 4b — 10 = 0 или 2 + 4b + 10 = 0
4b — 8 = 0 или 4b + 12 = 0

В правом уравнении получается отрицательное b. Оно нам не подходит, т.к. b — натуральное число. Левое уравнение даёт результат.

4b — 8 = 0
4b = 8
b = 8 / 4 = 2

В ответе получается 2.

Ответ: 2

Задача(Припиши справа b)

У исполнителя Сигмы две команды, которым присвоены номера:

1. вычти 1
2. припиши справа b
(b — неизвестная цифра)

Выполняя первую из них, Сигма уменьшает число на экране на 1, а выполняя вторую, приписывает к этому числу справа b.

Алгоритм для исполнителя Сигма — это последовательность номеров команд.

Известно, что алгоритм 12121 переводит число 3 в число 244.

Определите число b.

Решение:

Действие приписать справа b — это значит умножить число на 10 и прибавить b. Пример: пусть b=3, применим эту команду к числу 4. Тогда 4*10 + 3 = 43.

Выполним программу с первоначальным числом 3.

3 — 1 = 2
2*10 + b = 20 + b
20 + b — 1 = 19 + b
(19 + b)*10 + b = 190 + 10*b + b = 190 + 11*b
190 + 11*b — 1 = 189 + 11*b

Конечный результат равен 244.

189 + 11*b = 244
11*b = 55
b = 5

В ответе получилось 5.

Ответ: 5

Источник

Карло вошел в каморку, сел на единственный стул у безногого стола и, повертев так и эдак полено, начал ножом вырезывать из него куклу.

А. Толстой. Золотой ключик

Глава I. ЧИСЛА

Числа являются основой не только математики, но и информатики. Невозможно представить работу за компьютером без знания чисел. Кроме того, явно или неявно числа пронизывают все гуманитарное образование.

В этой главе представлен информационный и компьютерный аспект чисел. Основные изучаемые понятия — кодовая таблица и байт.

Здесь рассмотрены четыре системы счисления: две «обычные» — школьная десятичная и римская, и две специальные компьютерные — двоичная и шестнадцатеричная.

Основой компьютерной грамотности является, безусловно, двоичная система счисления.

Изложение шестнадцатеричной системы носит ознакомительный характер.

Дальнейшее изучение предмета может проводиться по двум направлениям: более полное изучение алгоритмов перевода чисел из одной системы в другую и рассмотрение систем счисления с другими основаниями.

§1. Обычные системы счисления

п. 1. Число

Определение 1. Число.

Число — основное понятие математики, которым передается информация. Число обычно означает три подпонятия:

1)количество, размер, вес, объем и т. д.;

2)порядковый номер, расположение в последовательности и т. д.;

3)элемент кода, шифра и т. д., которыми закодирована информация.

Мы будем иметь дело с простейшим видом чисел — множеством целых неотрицательных чисел, которое начинается с нуля и продолжается до бесконечности.

Определение 2. Натуральное число.

В информатике натуральными называются следующие числа:

0, 1, 2, 3, 4, …

Отметим, что в математике эти числа представляют расширенное множество натуральных чисел, дополненное нулем, а натуральными числами называются те же числа, но без нуля.

п. 2. Цифра

Для представления и записи чисел используют специальные графические знаки — цифры. Например, число 256 состоит из трех цифр 2, 5 и 6, число 16 состоит из двух цифр 1 и 6, а число 0 — из одной цифры 0.

Определение 3. Цифра.

Цифра — условный знак для обозначения числа. Число не состоит из цифр, а записывается, кодируются цифрами; из цифр состоит запись числа.

Цифра в узком смысле — один из 10 знаков десятичной системы счисления

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

п. 3. Система счисления

Определение 4. Система счисления.

Система счисления, или просто счисление, или нумерация,— это система из двух объектов:

1)набора конкретных знаков-цифр;

2)системы приемов записи чисел этими цифрами.

§ 1. Обычные системы счисления

Различные системы счисления могут отличаться друг от друга по следующим трем признакам:

1)разное начертание цифр, которые обозначают одни и те же числа;

2)разные способы записи чисел цифрами (см. пп. 4 и 5);

3)разное количество цифр (см. п. 5).

Например, восточные арабы до сих пор используют совершенно ту же самую систему счисления, что и в большинстве западных стран, но начертание цифр у них иное (см. табл. 1).

Таблица 1. Современные западное и «арабское» начертание цифр

Современные западные цифры,	0	1	2	3	4	5	6	7	8	9
используемые в большинстве стран


Современные арабские цифры,

используемые в арабских странах

п. 4. Непозиционная система счисления

По способу записи чисел цифрами системы счисления бывают позиционные и непозиционные.

Определение 5. Непозиционная система счисления.

Непозиционная система счисления — это такая система счисления,

что в записи числа каждая цифра имеет всегда одно и то же значение, т. е. ее «вес» не зависит от местоположения в числе.

Римская система счисления является непозиционной. Примеры.

1.Число I в римской системе означает один.

2.Число II означает 1 + 1, т. е. два.

3.Число III — 1 + 1 + 1 = 3.

п. 5. Позиционная система счисления

Определение 6. Позиционная система счисления.

Позиционная система счисления характеризуется тем, что значение знака-цифры, «вес» цифры зависит от ее расположения в записи числа.

Примеры.

1.Число 1 в обычной десятичной системе счисления означает один.

2.В числе 11 первая цифра справа означает 1, а вторая цифра справа — уже 10, поэтому число 11 означает 1 + 10, т. е. одиннадцать.

3.Рассуждая аналогично, получаем, что число 111 = 100 + 10 + 1, т. е. означает сто одиннадцать.

§ 1. Обычные системы счисления

Так легко и естественно числа называются только в обычной десятичной системе счисления. Причина этого явления в том, что наш язык является десятичным.

Определение 7. Основание системы счисления.

Основание системы счисления — это количество цифр позиционной

системы счисления.

Позиционные системы отличаются друг от друга своим количеством цифр. Поэтому они именуется по своему основанию.

Примеры.

1.Десятичная система счисления.

2.Двоичная система счисления.

3.Шестнадцатеричная система счисления.

п. 6. Римская система счисления

Определение 8. Римская система счисления.

Римская система счисления — счисление древних римлян, используемое в современной цивилизации.

Вприл. 1 приведены числа от 1 до 100, записанные римскими цифрами.

Врусском языке римские цифры используются для написания:

1)века;

2)порядкового числительного;

3)месяца при написании даты и, очень редко:

4)года н. э. (нашей эры).

п. 7. Семь римских цифр

Римская система счисления имеет свое оригинальное начертание цифр. В частности, в этой системе отсутствует нуль.

Определение 9. Римская цифра.

Римская система основана на употреблении семи особых знаков — римских цифр, которые делятся на две группы.

1. Четыре знака десятичных разрядов

I = 1, X = 10, C = 100, M = 1000.

2. Три знака половин десятичных разрядов

V = 5, L = 50, D = 500.

§ 1. Обычные системы счисления

п. 8. Чтение римских цифр

Целые положительные числа можно записывать при помощи повторения римских цифр. Чтобы узнать, что означает число, записанное римскими цифрами, нужно воспользоваться двумя правилами (которые в книгах по математике записаны не полностью).

Определение 10. Правило сложения римских цифр.

Если все цифры в числе по значению не возрастают, если считать слева направо, то они складываются.

Примеры.

1.II = 2, VI = 6, XI = 11 — правильно.

2.IV = 6, XL = 60 — неправильно.

Определение 11. Правило вычитания римских цифр.

1.Сначала во всех парах, где меньшая цифра стоит перед большей, вычитается меньшая цифра из большей.

2.Затем полученные результаты вместе с нетронутыми цифрами подпадают под правило сложения и складываются.

Примеры.

1.IV = 4, XIV = 14, XXIX = 29 — правильно.

2.IVX = 6, IXX = 1 — неправильно.

Имеем алгоритм вычисления значения римских чисел.

1.Число просматривается слева направо по одной цифре. Если текущая цифра больше или равна следующей, то она прибавляется к значению числа.

2.Если текущая цифра меньше следующей, то из следующей цифры вычитается текущая, а результат прибавляется к значению числа.

3.Если цифра последняя, то она прибавляется к значению числа.

п. 9. Запись римских цифр

В предыдущем пункте римские числа расшифровывались. Рассмотрим алгоритм, по которому числа записываются римскими цифрами. Этой информации нет в книгах по математике.

Определение 12. Алгоритм записи римских цифр.

1.Число записывается слева направо максимально возможными цифрами.

2.Но если в п. 1 получается 4 одинаковых десятичных знака подряд, то тогда они заменяются этим десятичным знаком и следующим половинным.

3.Но если при замене в п. 2 десятичный знак оказывается между двумя

одинаковыми половинными, то эти 3 знака заменяются этим десятичным знаком и следующим десятичным.

§ 1. Обычные системы счисления

Примеры.

1.3 = III; 6 = VI; 11 = XI; 22 = XXII.

2.4 = IV, а не IIII; 45 = XLV, а не XXXXV.

3.9 = IX, а не VIIII или VIV; 19 = XIX, а не XVIIII или XVIV.

В качестве демонстрации выпишем в табл. 2 все единицы, десятки и сотни, записанные в римской системе счисления (в прил. 1 приведены все римские числа от 1 до 100).

Таблица 2. Единицы, десятки и сотни, записанные римскими цифрами

I	II	III	IV	V	VI	VII VIII	IX	X
X	XX	XXX	XL	L	LX	LXX LXXX	XC	C
C	CC	CCC	CD	D	DC	DCC DCCC	CM	M

п. 10. Десятичная система счисления

Определение 13. Десятичная система счисления.

Десятичная система счисления — это позиционная система счисления, состоящая из 10 разных цифр и изучаемая в школе:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Здесь значение цифры зависит от ее положения в записи числа. Примеры.

1.Если цифра 1 стоит в числе на первом месте справа, то она значит один, если на 2-м месте справа, то десять, на 3-м месте справа — сто, и т. д.

2.В числе 512 пять сотен, один десяток и две единицы.

п. 11. Количество цифр в числе

Определение 14. n-значное число.

Однозначное число записывается 1 цифрой; количество таких чисел совпадает с количеством цифр: 1-значных чисел всего 10: 0, 1, 2, …, 9.

Двузначное число записывается 2 цифрами.

Трехзначное число — 3 и т. д.

n-значное число записывается с помощью n цифр.

Однозначные числа легко превратить в двузначные без изменения их значения, записав их в виде 00, 01, 02, …, 09. Так можно сделать потому, что нули в начале числа не влияют на величину числа. Также однозначные и двузначные числа можно превратить в трехзначные и т. д.

§ 1. Обычные системы счисления

Подсчитаем количество однозначных, двузначных и т. д. до десятизначных чисел: однозначных чисел всего 10, двузначных — 100 и т. д.

Таблица 3. Количество однозначных, двузначных и т. д. чисел

	Количество	Количество чисел
	цифр в числе

1	10 = 101
2	100 = 102
3	1000 = 103
4	10 000 = 104
5	100 000 = 105
6	1 000 000	= 106
7	10 000 000	= 107
8	100 000 000	= 108
9	1 000 000 000 = 109
10	10 000 000 000 = 1010

п. 12. Код

Определение 15. Код.

Код — это правило отображения одного набора объектов или знаков в другой набор знаков без потери информации. При этом можно всегда однозначно возвратиться к прежнему набору объектов или знаков.

Например, любую информацию можно передать русским языком с помощью 33 букв русского алфавита и добавочных знаков препинания.

Определение 16. Кодирование

Кодирование — это представление, моделирование одного набора знаков другим с помощью кода.

Определение 17. Кодовая таблица

Кодовая таблица — это соответствие между набором знаков и их кодами, обычно разными числами.

Табл. 3 говорит о том, что однозначными десятичными числами можно закодировать 10 предметов, приписав каждому предмету одно из этих 10 однозначных десятичных чисел.

Двузначными десятичными числами можно закодировать 100 предметов, трехзначными — 1000 и т. д.

§ 1. Обычные системы счисления

п. 13. Аски-коды

В прил. 2 представлена самая распространенная и универсальная компьютерная кодовая таблица. Она показывает компьютерное кодирование букв английского алфавита, цифр и т. д.

Определение 18. Аски-коды

Символы кодовой таблицы из табл. 4 называются аски-кодами (ASCII). Аски-коды состоят из следующих четырех групп символов.

1.Большие и маленькие английские буквы.

2.Десять цифр.

3.Самые распространенные знаки препинания.

4.Специальные символы (то, что не вошло в первые три группы).

Например, пробел кодируется на компьютере десятичным числом 32, восклицательный знак ! — числом 33, цифра 1 — числом 49, прописная английская букваA — числом 65 (см. прил. 2).

Упражнения

1.Запишите текущую дату, правильно использовав римские цифры.

2.Переведите следующие римские числа в десятичные.

CCXXII; MMMXXX; CXCIV; MCMXIX.

3. Запишите римскими цифрами двумя разными неправильными способами числа 49 и 99.

4.Составьте таблицу, в которой перечислены все десятичные и римские числа от 1 до 100.

5.Переведите следующие десятичные числа в римские.

111; 555; 444; 999.

6. Найдите максимальное число, которое можно записать римскими цифрами.

7.В городе может быть построено не более миллиона строений, каждому присваивается инвентарный номер. Каждый инвентарный номер имеет одно и то же количество цифр. Какое должно быть минимальное количество цифр в инвентарном номере?

8.В стране немногим более 100 миллионов человек. Каждому человеку присваивается индивидуальный номер. Какова его минимальная длина?

§ 2. Недесятичные системы счисления

п. 1. Двоичная система счисления

Определение 19. Двоичная система счисления.

Двоичная система счисления — это позиционная система счисления, состоящая только из двух цифр:

0 и 1.

Это система счисления с минимальным основанием. Поэтому в компьютерах используется именно эта система. Простота выполнения операций

вдвоичной системе счисления связана с двумя обстоятельствами:

1)простотой аппаратной реализации: 1 — есть сигнал, 0 — нет сигнала;

2)самое сложное действие таблицы умножения — это 12 × 12 = 12, а самое сложное действие таблицы сложения — 12 + 12 = 102.

Почему в двоичной системе при сложении двух единиц счисления получается десять? Эта ситуация аналогична той, когда в десятичной системе

к девяти прибавляется один: 910 + 110 = 1010. На девятке цифры десятичной системы заканчиваются, и затем следует наименьшее двузначное число

десять 1010. В двоичной системе цифры заканчиваются на единице, и после нее идет наименьшее двузначное число десять 102.

Двойка внизу в виде нижнего индекса означает, что числа записаны в двоичной системе. При записи чисел в разных позиционных системах счисления основание системы записывается в виде нижнего индекса. Этот индекс всегда записывается только в десятичной системе счисления.

п. 2. Таблицы умножения и сложения

Запишем таблицы умножения и сложения для двоичной системы (табл. 5 и 6). Отметим, что таблица сложения сложнее таблицы умножения.

Таблица 5. Таблица умножения двоичных чисел

Таблица 6. Таблица сложения двоичных чисел

+	0	1
0	0	1
1	1	102
	19

п. 3. Натуральные двоичные числа

Выпишем первые натуральные двоичные числа от 0 до 16. Цифровую запись следующего числа можно получить, используя основное свойство натуральных чисел: следующее число больше предыдущего на 1.

Поэтому для получения следующего двоичного числа после 12 прибавим к 12 число 12, получим 12 + 12 = 102, т. е. «десять». Отсюда имеем:

210 = 12 + 12 = 102 (см. рис. 1).

Столбиком посчитаем следующие по порядку двоичные числа, т. е. прибавим 12 к 102 , затем к 112 и т. д. (см. рис. 1)

1	102	1	1
	2
+ 1	+ 1		11
+	12
102	112
		100

Рис. 1. Получение первых двоичных чисел

Продолжая аналогичным образом, заполним всю табл. 7.

Таблица 7. Первые двоичные натуральные числа от 0 до 16

Десятичное число		Двоичное число


0		0
1		1
210		102
310		112
410		1002
510		1012
610		1102
710		1112
810		10002
910		10012
1010		10102
1110		10112
1210		11002
1310		11012
1410		11102
1510		11112
1610		100002

	20

Соседние файлы в предмете Информатика

Источник

Скачать материал

Сейчас обучается 26 человек из 17 регионов

Сейчас обучается 46 человек из 24 регионов

Описание презентации по отдельным слайдам:

1 слайд

РАЗБОР Задания №5
КЕГЭ — 2021
ГОТОВИМСЯ К ЕГЭ ПО ИНФОРМАТИКЕ
2 слайд

Проверяемые
элементы содержания по спецификации
Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд

Элементы содержания, проверяемые на ЕГЭ
Построение алгоритмов и практические вычисления
Проверяемые умения или способы действий
Строить информационные модели объектов, систем и процессов в виде алгоритмов
3 слайд

Алгоритм получает на вход натуральное число N и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. Складываются все цифры полученной двоичной записи. В конец записи (справа) дописывается остаток от деления суммы на 2.
3. Предыдущий пункт повторяется для записи с добавленной цифрой.
4. Результат переводится в десятичную систему.
Пример. Дано число N = 13. Алгоритм работает следующим образом:
Двоичная запись числа N: 1101.
Сумма цифр двоичной записи 3, остаток от деления на 2 равен 1, новая запись 11011.
Сумма цифр полученной записи 4, остаток от деления на 2 равен 0, новая запись 110110.
Результат работы алгоритма R = 54.
При каком наименьшем числе N в результате работы алгоритма получится R > 170? В ответе запишите это число в десятичной системе счисления.
4 слайд

N
R
По условию нужно получить R>170
Допустим, что R=170, переведем в двоичную систему счисления.
Метод разностей
170
128
42
32
10
8
2
N
В числе N в сумме 3 единицы, справа дописали единицу, остаток от деления на 2.
После этого в числе стало 4 единицы. Справа дописали 0, остаток от деления на 2.
! Иногда стоит проверить, соответствует ли число R заданному алгоритму
Последние две цифры нам не нужны, далее мы их не используем, т.к. изначально все действия производились с числом N.
N=1010102 При этом число R=170, значит чтобы получилось минимально большее число надо +1. N=1010112 Т.к. нам нужно найти N, переведем его в десятичную систему счисления 101011 2 =32+8+2+1=43
Ответ: 43
5 слайд

Автомат обрабатывает натуральное число N по следующему алгоритму:
Строится двоичная запись числа N.
В конец двоичной записи добавляются две первые цифры этой записи в обратном порядке.
Результат переводится в десятичную систему и выводится на экран.
Пример. Дано число N = 11.
Алгоритм работает следующим образом:
Двоичная запись числа N: 1011.
В конец записи добавляются цифры 01 – первые две цифры в обратном порядке (сначала вторая, затем первая), получается 101101.
На экран выводится число 45.

При каком наименьшем исходном N результат на экране автомата будет больше 90?
Переведем число R=90 в двоичную систему.

90
64
26
16
10
8
2
N
Число образовано не по алгоритму, но если поменять местами последние две цифры, получим число меньше 90. Значит увеличим число N на единицу. N=101112 Переведем его в десятичную систему счисления 10111 2 =16+4+2+1=23
Ответ: N=23
6 слайд

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается справа бит чётности: 0, если в двоичном коде числа N было чётное число единиц, и 1, если нечётное.
3) К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите максимальное число R, меньшее 125, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.
! Найти нужно число R
125=1111101 2
Обращаем внимание, что число построено не по алгоритму.
1111110 2, но это число больше 125 (126), поэтому работаем с числом N.
Уменьшаем число N на единицу 11111 2 -1=11110 2
Строим новое число R – 1111000 2
Переводим его в десятичную систему. 127-7=120
Ответ: R=120
7 слайд

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) Складываются все цифры двоичной записи числа. Если сумма четная, то в конец числа (справа) дописывается 1, а если нечетная, то дописывается 0. Например, запись числа 10 преобразуется в запись 100;
К полученному результату применяется еще раз пункт 2 этого алгоритма.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите количество чисел R, которые могут быть получены в результате работы этого алгоритма, и лежат в диапазоне 16 ≤ R ≤ 32.
1. Переведем 16 и 32 в двоичную систему.
16=10000 2
32=100000 2
2. Удалим последние два бита.
100 2 = 410
1000 2 = 810
Последние два бита можно дописать по алгоритму но в диапазоне от 4 до 8 всего 5 чисел.
(8-4+1=5)
Ответ: 5 чисел
8 слайд

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается (дублируется) последняя цифра.
3) Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4) К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, большее 114, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.
Переведем 114 двоичную систему. R=1110010 2
Удалим 3 последние цифры.
N=1110 2 +1=1111 2
Построим новое число R=1111110 2
Переведем в десятичную систему R=126
Ответ: R=126
9 слайд

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается (дублируется) последняя цифра.
3) Затем справа дописывается 0, если в двоичном коде числа N чётное число единиц, и 1, если нечётное.
4) К полученному результату дописывается ещё один бит чётности так, чтобы количество единиц в двоичной записи полученного числа стало чётным.
Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, большее 80, которое могло получиться в результате работы автомата. В ответе это число запишите в десятичной системе.
Переведем 80 двоичную систему. R=1010000 2
Удалим 3 последние цифры.
N=1010+1=1011 2
Построим новое число R=1011111 2
Переведем в десятичную систему R=95
Ответ: R=95
10 слайд

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3) Полученное число переводится в десятичную запись.
4) Из нового числа вычитается исходное, полученная разность выводится на экран.
Пример. Дано число N = 13. Алгоритм работает следующим образом:
1) Восьмибитная двоичная запись числа N: 00001101.
2) Все цифры заменяются на противоположные, новая запись 11110010.
3) Десятичное значение полученного числа 242.
4) На экран выводится число 242 – 13 = 229.
Какое число нужно ввести в автомат, чтобы в результате получилось 113?
Переведем число 113 в двоичную систему.
113=1110001 2
Запись должна быть восьмибитная, поэтому результат вычитания равен 01110001 2
Х – Y= 01110001 2 При этом цифры числа Y должны быть инвертированы.
Например, Х=101, Y=010
Вычитаем – исходное число 1000111 2
Переводим в десятичную систему
Ответ: 71
Новое число
Исходное число
Понимать !
11 слайд

Автомат обрабатывает натуральное число N < 256 по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N–1.
2) Инвертируются разряды исходного числа (0 заменяется на 1, 1 на 0).
3) Полученное число переводится в десятичную систему счисления.
Для какого числа N результат работы алгоритма равен 18?
Число 18.
Переведем в двоичную систему 18=10010 2
Строим восьмибитную запись 00010010 2
Инвертируем цифры – 11101101 2
Прибавить единицу – 11101101 2 +1=11101110 2
Переведем в десятичную систему
Ответ: 238
12 слайд

Материалы для подготовки
https://kpolyakov.spb.ru/ — сайт ПОЛЯКОВА Константина Юрьевича

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 263 940 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

14.02.2021
497
17

14.02.2021
1008
6

14.02.2021
360
4

14.02.2021
1200
105

Вам будут интересны эти курсы:

Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс повышения квалификации «Современные тенденции цифровизации образования»
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»

Источник

Проверка натурального числа

Условие задачи 1.1

Что такое натуральное число

Что такое действительное число

Как проверить натуральное число

Проверка действительного числа

Проверка числовой последовательности на соответствие алгоритму

Разбор 5 задания

Решение задания про алгоритм, который строит число R

Решение заданий для темы Проверка числовой последовательности (Автомат)

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Не пропустите также: