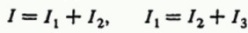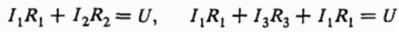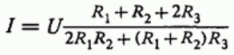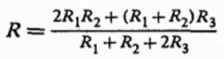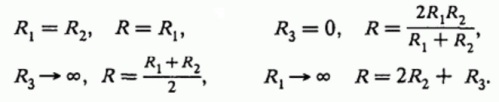Как найти напряженность при параллельном напряжении

Ток и напряжение при параллельном, последовательном и смешанном соединении проводников

Реальные электрические цепи чаще всего включают в себя не один проводник, а несколько проводников, как-то соединенных друг с другом. В самом простом виде электрическая цепь имеет только «вход» и «выход», то есть два вывода для соединения с другими проводниками, через которые заряд (ток) имеет возможность втекать в цепь и из цепи вытекать. При установившемся токе в цепи, значения величин токов на входе и на выходе будут одинаковы.

Если взглянуть на электрическую цепь, включающую в себя несколько разных проводников, и рассмотреть на ней пару точек (вход и выход), то в принципе остальная часть цепи может быть рассмотрена как одиночный резистор (по ее эквивалентному сопротивлению).

При таком подходе говорят, что если ток I – это ток в цепи, а напряжение U – напряжение на выводах, то есть разность электрических потенциалов между точками «входа» и «выхода», то тогда отношение U/I можно рассмотреть как величину эквивалентного сопротивления R цепи целиком.

Если закон Ома выполняется, то эквивалентное сопротивление можно вычислить довольно легко.

Ток и напряжение при последовательном соединении проводников

В простейшем случае, когда два и более проводников объединены друг с другом в последовательную цепь, ток в каждом проводнике окажется одним и тем же, а напряжение между «выходом» и «входом», то есть на выводах всей цепи, будет равным сумме напряжений на составляющих цепь резисторах. И поскольку закон Ома справедлив для любого из резисторов, то можно записать:

Итак, для последовательного соединения проводников характерны следующие закономерности:

Для нахождения общего сопротивления цепи, сопротивления составляющих цепь проводников складываются;

Ток через цепь равен току через любой из проводников, образующих цепь;

Напряжение на выводах цепи равно сумме напряжений на каждом из проводников, образующих цепь.

Ток и напряжение при параллельном соединении проводников

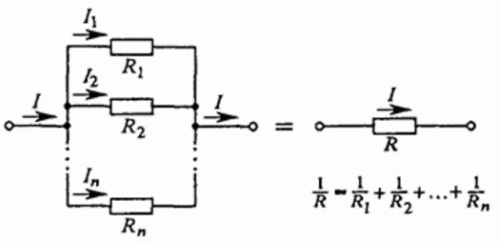
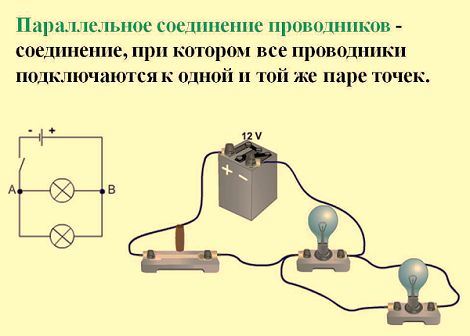
При параллельном соединении нескольких проводников друг с другом, напряжение на выводах такой цепи — это напряжение на каждом из проводников, составляющих цепь.

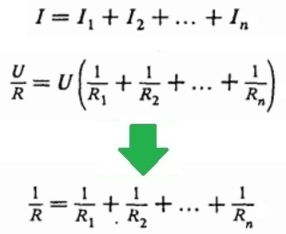
Напряжения на всех проводниках равны между собой и равны напряжению приложенному (U). Ток через всю цепь — на «входе» и «выходе» — равен сумме токов в каждой из ветвей цепи, параллельно объединенных и составляющих данную цепь. Зная, что I = U/R, получаем, что:

Итак, для параллельного соединения проводников характерны следующие закономерности:

Для нахождения общего сопротивления цепи — складываются обратные величины сопротивлений составляющих цепь проводников;

Ток через цепь равен сумме токов через каждый из проводников, образующих цепь;

Напряжение на выводах цепи равно напряжению на любом из проводников, образующих цепь.

Эквивалентные схемы простых и сложных (комбинированных) цепей

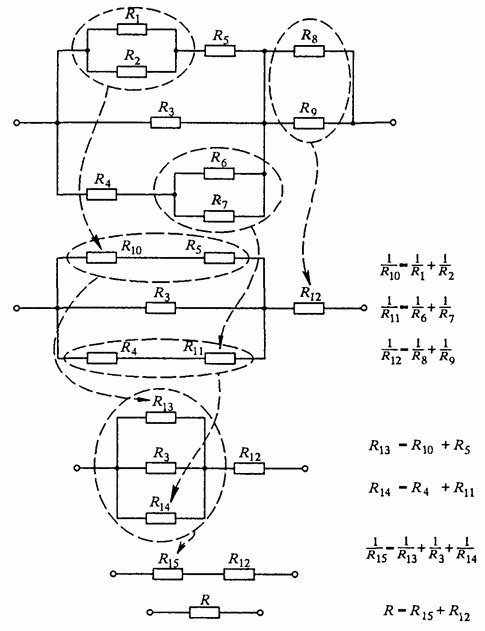
В большинстве случаев схемы цепей, являясь комбинированным соединением проводников, поддаются пошаговому упрощению.

Группы соединенных последовательно и параллельно частей цепи, заменяют эквивалентными сопротивлениями по приведенному выше принципу, шаг за шагом вычисляя эквивалентные сопротивления кусочков, затем приводя их к одному эквивалентному значению сопротивления всей цепи.

И если сначала схема выглядит довольно запутанной, то будучи упрощенной шаг за шагом, она может быть разбита на меньшие цепочки из последовательно и параллельно соединенных проводников, и так в конце концов сильно упрощена.

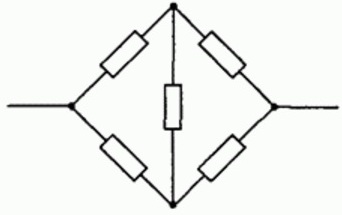
Между тем, не все схемы подаются упрощению таким простым путем. Простая с виду схема «моста» из проводников не может быть исследована таким образом. Здесь нужно применять уже несколько правил:

Для каждого резистора выполняется закон Ома;

В любом узле, то есть в точке схождения двух и более токов, алгебраическая сумма токов равна нулю: сумма токов втекающих в узел, равна сумме токов вытекающих из узла (первое правило Кирхгофа);

Сумма напряжений на участках цепи при обходе по любому пути от «входа» до «выхода» равна приложенному к цепи напряжению (второе правило Кирхгофа).

Мостовое соединение проводников

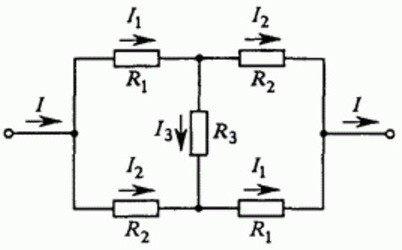
Дабы рассмотреть пример использования приведенных выше правил, рассчитаем цепь, собранную из проводников, объединенных в схему моста. Чтобы вычисления получились не слишком сложными, примем, что некоторые из сопротивлений проводников равны между собой.

Обозначим направления токов I, I1, I2, I3 на пути от «входа» в цепь — к «выходу» из цепи. Видно, что схема симметрична, поэтому токи через одинаковые резисторы одинаковы, поэтому обозначим их одинаковыми символами. В самом деле, если поменять у цепи местами «вход» и «выход», то схема будет неотличима от исходной.

Для каждого узла можно записать уравнения токов, исходя из того, что сумма токов втекающих в узел равна сумме токов вытекающих из узла (закон сохранения электрического заряда), получится два уравнения:

Следующим шагом записывают уравнения сумм напряжений для отдельных участков цепи при обходе цепи от входя к выходу различными путями. Так как схема является в данном примере симметричной, то достаточно двух уравнений:

В процессе решения системы линейных уравнений, получается формула для нахождения величины тока I между зажимами «входным» и «выходным», исходя из заданного приложенного к цепи напряжения U и сопротивлений проводников:

А для общего эквивалентного сопротивления цепи, исходя из того, что R = U/I, следует формула:

Можно даже проверить правильность решения, например приведя к предельным и к частным случаям величины сопротивлений:

Теперь вы знаете, как находить ток и напряжение при параллельном, последовательном, смешанном, и даже при мостовом соединении проводников, применяя закон Ома и правила Кирхгофа. Эти принципы очень просты, и даже самая сложная электрическая цепь с их помощью в конце концов приводится к элементарному виду путем нескольких несложных математических операций.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Последовательное и параллельное соединение

Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.

Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м 2

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R_AB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

Если бы у нас еще были резисторы, соединенные параллельно, то для них

В этом случае, сила тока в цепи будет равна:

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Воспользуемся формулами, которые приводили выше.

Если бы у нас еще были резисторы, соединенные параллельно, то для них

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

2-ой способ найти I

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Источник

Расчет электрической цепи, рассмотренный в предыдущей статье, можно распространить на цепи, содержащие произвольное число приемников, соединенных параллельно.

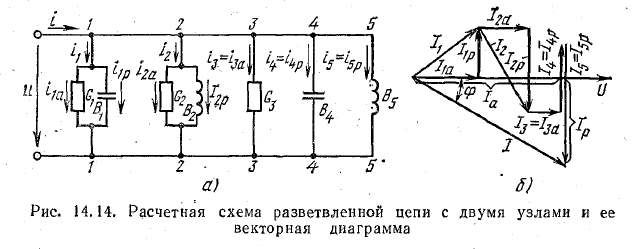
На рис. 14.14, а параллельно соединены те же элементы цепи, которые были рассмотрены при последовательном соединении (см. рис. 14.7, а). Предположим, что для этой цепи известны напряжение u = U_msinωt. и параметры элементов цепи R, L, С. Требуется найти токи в цепи и мощность.

Векторная диаграмма для цепи с параллельным соединением ветвей. Метод векторных диаграмм

Для мгновенных величин в соответствии с первым законом Кирхгофа уравнение токов

Представляя ток в каждой ветви суммой активной и реактивной составляющих, получим

Для действующих токов нужно написать векторное уравнение

Численные значения векторов токов определяются произведением напряжения и проводимости соответствующей ветви.

На рис. 14.14, б построена векторная диаграмма, соответствующая этому уравнению. За исходный вектор принят, как обычно при расчете цепей с параллельным соединением ветвей, вектор напряжения U, а затем нанесены векторы тока в каждой ветви, причем направления их относительно вектора напряжения выбраны в соответствии с характером проводимости ветвей. Начальной точкой при построении диаграммы токов выбрана точка, совпадающая с началом вектора напряжения. Из этой точки проведен вектор l_1a активного тока ветви I (по фазе совпадает c напряжением), а из конца его проведен вектор I_1p реактивного тока той же ветви (опережает напряжение на 90°). Эти два вектора являются составляющими вектора I₁ тока первой ветви. Далее в том же порядке отложены векторы токов других ветвей. Следует обратить внимание на то, что проводимость ветви 3-3 активная, поэтому реактивная составляющая тока в этой ветви равна нулю. В ветвях 4-4 и 5-5 проводимости реактивные, поэтому в составе этих токов нет активных составляющих.

Расчетные формулы для цепи с параллельным соединением ветвей. Метод векторных диаграмм

Из векторной диаграммы видно, что все активные составляющие векторов тока направлены одинаково — параллельно вектору напряжения, поэтому векторное сложение их можно заменить арифметическими найти активную составляющую общего тока: I_а = I_1a + I_2a + I_3a.

Реактивные составляющие векторов токов перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая общего тока в цепи определяется их алгебраической суммой, в которой индуктивные токи считаются положительными, а емкостные — отрицательными: I_p = — I_1p + I_2p — I_4p + I_5p.

Векторы активного, реактивного и полного тока всей цепи образуют прямоугольный треугольник, из которого следует

Подставив величины токов в ветвях, выраженные через напряжение и соответствующие проводимости, получим

где ∑Gn — общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей; ∑Bn — общая реактивная
проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;

Таким образом получена знакомая уже формула (14.12), связывающая напряжение, ток и проводимость цепи [ср. (14.12) и (14.8)].

Следует обратить внимание на возможные ошибки при определении полной проводимости цепи по известным проводимостям отдельных ветвей: нельзя складывать арифметически проводимости ветвей, если токи в них не совпадают по фазе.

Полную проводимость цепи в общем случае определяют как гипотенузу прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активная и реактивная проводимости всей цепи:

От треугольника токов можно перейти также к треугольнику мощностей и для определения мощности получить известные уже формулы

Активную мощность цепи можно представить как арифметическую сумму активных мощностей ветвей.

Реактивная мощность цепи равна алгебраической сумме мощностей ветвей. В этом случае индуктивная мощность берется положительной, а емкостная — отрицательной:

Расчет цепи без определения проводимостей ветвей

Расчет электрической цепи при параллельном соединении ветвей можно выполнить без предварительного определения активных и реактивных проводимостей, т. е. представляя элементы цепи в схеме замещения их активными и реактивными сопротивлениями (рис. 14.15, а).

Определяют токи в ветвях по формуле (14.4);

где Z₁, Z₂ и т. д. — полные сопротивления ветвей.

Полное сопротивление ветви, в которую входят несколько элементов, соединенных последовательно, определяют по формуле (14.5).

Для построения векторной диаграммы токов (рис. 14.15, б) можно определить активную и реактивную составляющие тока каждой ветви по формулам

и т. д. для всех ветвей.

В этом случае отпадает необходимость определения углов ф₁ ф₂ и построения их на чертеже.

Ток в неразветвленной части цепи

Общий ток и мощность цепи определяются далее в том же порядке, какой был показан ранее (см. формулы (14.10), (14.15), (14.16)].

Задача

Параллельное соединение

Параллельным
называется соединение проводников,
при котором одни их концы образуют узел
А, а другие – узел В.

Узловые
точки
(узлы)
– это точки, в которых сходятся не
менее трех проводников.

Параллельно
соединенные проводники составляют
разветвление,
а каждая из
них называется
ветвью.

1.
При параллельном соединении
напряжения
на всех
ветвях и на всем разветвлении одинаковы,
(как разности
потенциалов двух точек А и В):
U₁=U₂=U.

По первому
правилу Кирхгофа
(алгебраическая сумма токов, сходящихся
в одном узле, равно нулю), имеем:

2. Сумма токов
I₁ + I₂,
протекающих по ветвям, равна силе тока
I
в неразветвленной части цепи:
I = I₁ + I₂

Этот результат
следует из того, что
в точках разветвления токов (узлы A
и B)
в цепи постоянного тока не могут
накапливаться заряды.
Следовательно, I = I₁ + I₂

3. Токи
в отдельных ветвях разветвления обратно
пропорциональны сопротивлениям этих
ветвей:


=

_/

На
основании закона Ома: U₁ = I₁·R₁,  U₂ = I₂·R₂
и
учитывая,
что напряжения на ветвях одинаковы
U₁ = U₂ = U,

имеем:
I₁
R₁ = I₂
R₂ 
или

= ,

т.
е.

=

_/

5.
При
параллельном соединении проводников
величина, обратная эквивалентному
(полному) сопротивлению участка цепи,
равна сумме величин, обратных сопротивлению
отдельных проводников.

Записывая
на основании закона Ома:
,,,
где R
– электрическое сопротивление всей
цепи (из двух ветвей), получим, учитывая,
что напряжения одинаковы на ветвях:
.
Для трех проводников:

или:
R_ЭКВ=

При
параллельном соединении двух проводников
формула упрощается: R_ЭКВ.
= 

Этот
результат справедлив для
любого числа
параллельно включенных проводников.

Величина,
обратная сопротивлению, называется
проводимостью проводников:
g
=
.
Тогда:g_ПАР=
g₁
+ g₂
+ g₃.

Единица
проводимости – сименс,
См. 1 См = 1 Ом
^-1.
Сименс – электрическая
проводимость проводника сопротивлением
в 1 Ом.

Если
соединены параллельно n
одинаковых проводников, то эквивалентное
сопротивление равно величине одного,
деленное на число ветвей разветвления
n:
R_ПАР
=.
При параллельном соединении проводников
эквивалентное
сопротивление меньше
наименьшего
из сопротивлений. При этом общий ток
в цепи равен: I_ПАР=
I₁
·n

Если напряжение
между узлами остается постоянным, то
токи в ветвях не зависят друг от друга.
Из этого следует, что на практике для
потребителей удобнее пользоваться
параллельным соединением.

4. Расширение пределов измерения амперметра и вольтметра

Задача.
Предел измерения амперметра Iа
= 2А. Каким образом можно измерить силу
тока I
= 10 А, если внутреннее сопротивление
амперметра равен Rа
= 0,4 Ом?

Решение.
А)
Для расширения предела измерения
параллельно к амперметру присоединяют
шунт сопротивлением Rш,
через который будет проходить ток,
равный Iш
=
I
– Iа.
Напряжение на шунте и амперметре будут
одинаковы и равны U
= Iа
_·Rа
= Iш·Rш

Отсюда
получаем: Rш
=;
Rш
=Разделим числитель и знаменатель наIа,
обозначим n
=
,
тогда получим:
Rш
=

Подставив
числовые значения,
получаем
Rш
=
= 0,1 Ом

В)
Или решаем по готовой формуле
Rш
=

,
где
n
=
.
Вычислим:
n
=
=
5;
Rш
===
0,1 Ом

Ответ.
Параллельно к амперметру присоединить
шунт сопротивлением R_Ш
= 0,1Ом

Задача. А)
Сопротивление
вольтметра Rв=400
Ом, предел измерения Uв=
6В. Что необходимо сделать, чтобы данным
вольтметром можно было измерить
напряжение до U
= 42 В?

Решение. А)
Для расширения предела измерений к
вольтметру присоединяют дополнительное
сопротивление Uд
=
U
– Uв

Сила тока,
проходящего через вольтметр и
дополнительное сопротивление, одинакова.
Из закона Ома для участка цепи имеем:

I
=_;
I
=

= I
=

Отсюда:
=

и Rд=

Разделим на Uв
числитель и знаменатель. Обозначим n
=.
Тогда
получим: Rд
=Rв
· (n
– 1)
Rд

=
= 2400 Ом

В) Или по формуле:
Rд
= Rв
· (n
– 1), где n
=
.
Вычислим:
n
=
=
7;Rд
= 400 В ·(7– 1) = 2400 Ом; Rд
=
2400 Ом

Ответ.
Последовательно с вольтметром надо
присоединить (добавку) резистор с
сопротивлением R_Д
=
2400 Ом

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие разным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно заранее учитывать при проектировании цепей.

Последовательное соединение проводников

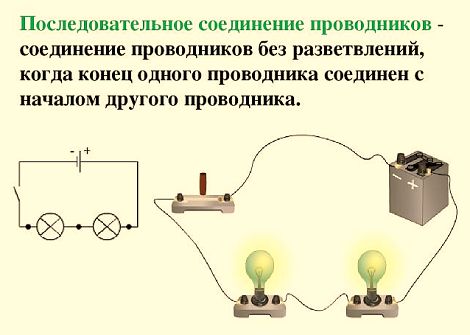
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R – общее сопротивление, R1 – сопротивление одного элемента, а n – количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является елочная гирлянда, когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный амперметр. Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 – силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 – сопротивления обеих лампочек, U = U1 = U2 – значение напряжения, показываемое вольтметром.

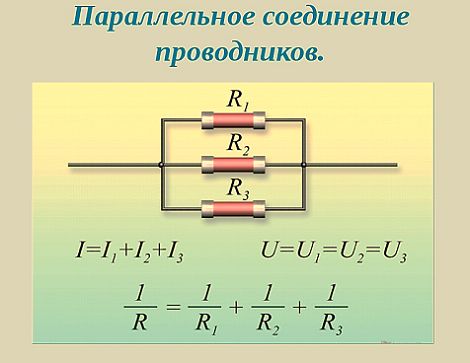
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях – увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

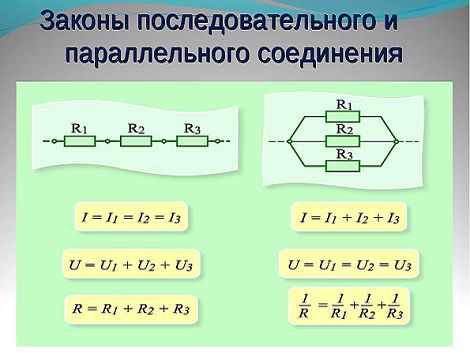
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• Закон ома параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

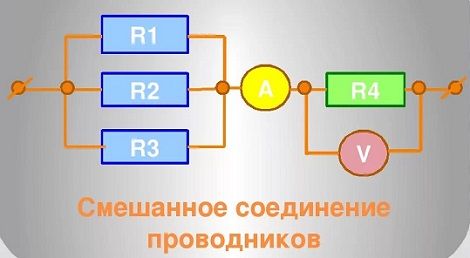
Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Иногда в наличии нет конденсатора с нужными параметрами. В таком случае, можно соединить несколько конденсаторов так, чтобы полученная система обладала необходимой электрической емкостью. Существуют два основных способа соединений:

1. параллельный;
2. последовательный;

Комбинируя эти способы, можно получить смешанное соединение.

Для каждого способа применяют специальные формулы, описывающие распределение заряда и напряжения на конденсаторах, а, так же, получаемую итоговую электроемкость системы.

Параллельное соединение

Этот способ соединения получаем, соединяя каждый вывод одного прибора с соответствующим ему выводом другого (рис. 1).

Емкость для параллельного включения можно определить так:

[large boxed { C_{1} + C_{2} = C_{text{общ}} } ]

При этом, общая (large C_{text{Общ}} ) электроемкость получится больше самой большой емкости, входящей в соединение.

(large C_{1}, C_{2} left( text{Ф} right) ) – электроемкости конденсаторов.

Общая электроемкость включенных параллельно конденсаторов больше емкости большего из них.

Напряжение на конденсаторах

Напряжения, приложенные к параллельно подключенным обкладкам, равны.

[large boxed { U_{1} = U_{2} = U_{text{общ}} } ]

(large U_{1}, U_{2}left( Bright) ) – напряжения на обкладках.

Правило для зарядов

Общий заряд системы разделится на части. Каждая из параллельно соединенных емкостей получит свой заряд.

[large boxed { q_{1} + q_{2} = q_{text{общ}} } ]

(large q_{1}, q_{2}left( text{Кл} right) ) – заряды на конденсаторах.

При этом, из формулы емкости (ссылка), связывающей ее с напряжением на обкладках и зарядом, следует (рис. 4):

При параллельном соединении меньшая емкость содержит меньший заряд.

Из рисунка 4 следует, в параллельной части цепи конденсатор с наименьшей (0,1 Ф) электроемкостью накапливает меньший (1 Кулон) заряд. А набиольший заряд 4 Кулона содержится на приборе, обладающем максимальной емкостью 0,4 Ф.

Последовательное соединение

Для такого способа соединения складываются величины, обратные емкостям.

[large boxed { frac {1}{C_{1}} + frac {1}{C_{2}} = frac {1}{C_{text{общ}}} } ]

Примечание: Величина, обратно пропорциональная емкости, измеряется в обратных Фарадах.

(large displaystyle frac {1}{C} left( frac {1}{text{Ф}} right) ) – величину, обратную электроемкости в некоторых источниках называют электрической эластичностью (эластансом).

(large C_{1}, C_{2}left( text{Ф}right) ) – емкости конденсаторов.

При последовательном включении общая (large C_{text{Общ}} ) электроемкость цепочки окажется меньше самой маленькой емкости включенной в цепочку.

Общая емкость системы меньше меньшей из включенных последовательно емкостей.

Правило для напряжений

Приложенное к концам последовательной цепочки напряжение распределится между элементами.

[large boxed { U_{1} + U_{2} = U_{text{общ}} } ]

где (large U_{1}, U_{2}left( Bright) ) — это напряжения на обкладках.

Чем больше емкость конденсатора, тем меньшее напряжение будет наблюдаться на его обкладках при последовательном соединении.

Общее напряжение разделится на части. Большее напряжение будет на конденсаторе с меньшей электроемкостью.

На рисунке 7 представлена цепочка, состоящая из 4-ех емкостей, соединенных последовательно. На конденсаторе с наименьшей емкостью 0,3 Ф напряжение составляет 4 Вольта.

А наименьшее напряжение 1 Вольт, находится на обкладках конденсатора с наибольшей емкостью 1,2 Ф. Общее напряжение на концах цепочки равняется 10-и Вольтам.

Заряд на конденсаторах

Зарядив одну из обкладок конденсатора, мы получим на второй его обкладке такой же (по модулю) заряд противоположного знака. Поэтому, все конденсаторы, соединенные последовательно, будут иметь одинаковые заряды на обкладках.

[large boxed { q_{1} = q_{2} = q_{text{общ}} } ]

где (large q_{1}, q_{2}left( text{Кл} right) ) – заряды, накопленные конденсаторами.

В последовательно включенной цепочке все конденсаторы обладают равными зарядами.

Выводы

1. Правила, приведенные в статье, будут справедливы не только для двух, но и для любого количества включенных конденсаторов.
2. Связывающие напряжения и заряды формулы для последовательно и параллельно включенных элементов, можно получить из принципа сложения емкостей и обратных емкостей, а, так же, отношения между приложенным напряжением и зарядом.