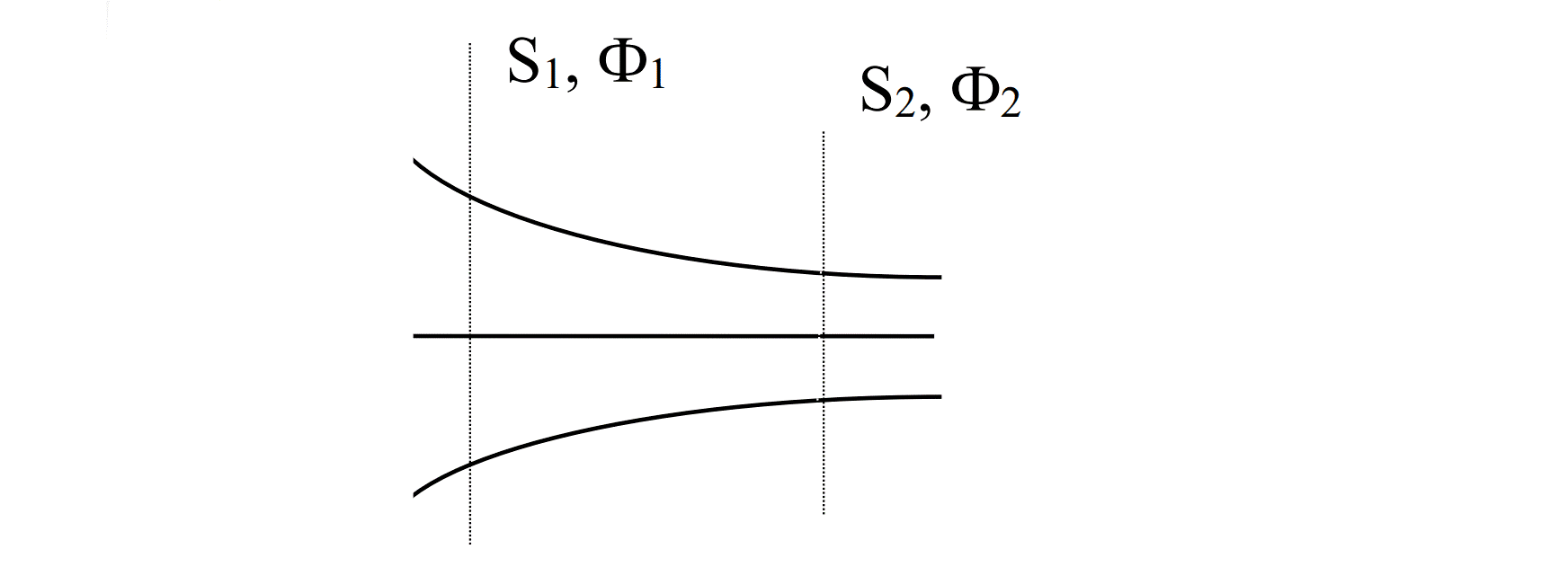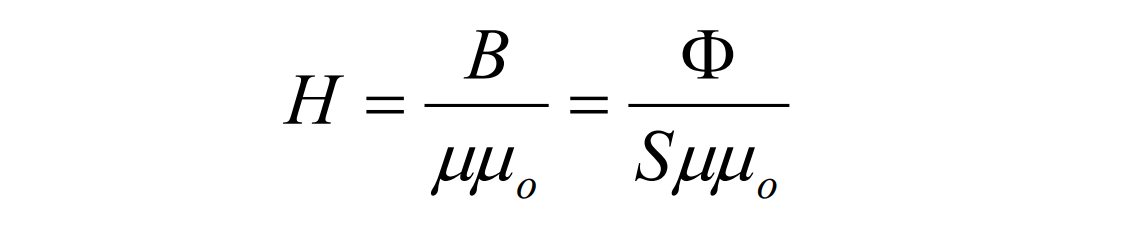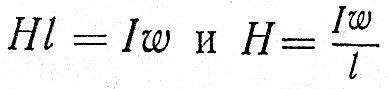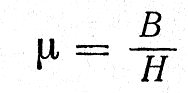Ток или поток? Магнитные цепи и их основные характеристики
Время на прочтение
6 мин
Количество просмотров 13K
Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это… а что это такое?
Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.
Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим.
Что нужно вспомнить?
Для более четкого представления сей статьи, неплохо бы вспомнить основные характеристики самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции — а также нужно вспомнить немного про магнитные вещества, а именно про ферромагнетики.
Полагается, что вам известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то крайне советую обратиться к сторонним ресурсам, чтобы иметь хотя бы общее представление о том, что последует далее. Крайне советую учебник И.Е. Иродова «Электромагнетизм».
Применение магнитных цепей
Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.
Конечно, можно продолжительное время говорить об устройствах, разных типах магнитопроводов (про которые речь пойдет далее), но наша первичная цель — рассмотреть выводы основных характеристик магнитных цепей. Продолжаем!
Как устроены магнитные цепи?
Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:
Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».
Начнем с тороидального сердечника. Такой тороидальный сердечник может служить формой для катушки, как бы странно это не звучало. Но что за катушка? Ну, первое что приходит в голову — провод, образующий витки. Хорошо, но какого его предназначение? Вернемся к электрическим цепям и вспомним, что существуют источники тока / напряжения, так называемые активные элементы. Так вот, в магнитных цепях роль источника выполняют катушки с током, накрученные на основной элемент магнитной цепи — ферромагнитный магнитопровод.
Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:
Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.
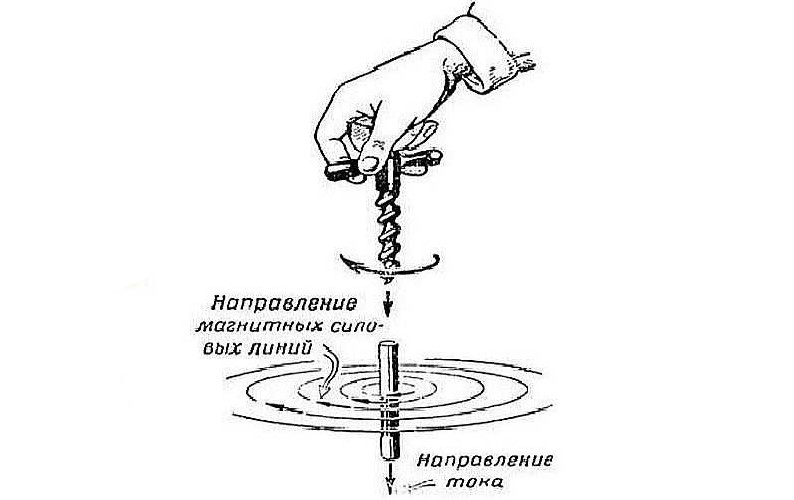
Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.
Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения.*
Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.
Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.
1] Магнитные потоки Ф1 и Ф2 через произвольные сечения будут равны между собой.
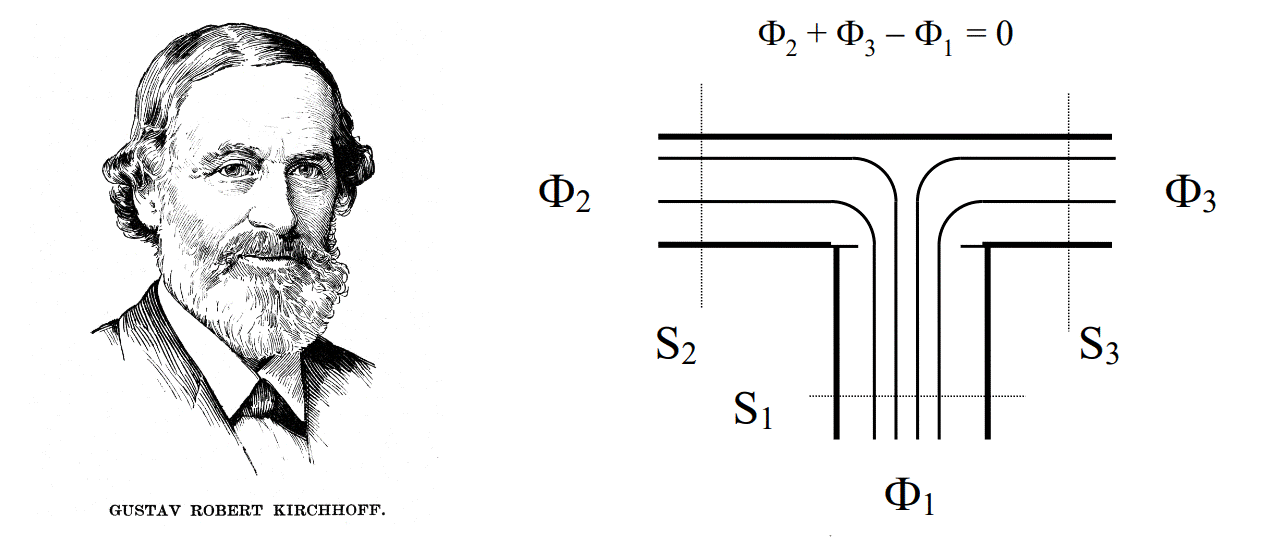
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю… Мне одному это что-то напоминает?
То есть мы окончательно сформулировали, что замкнутая (или почти замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае — магнитная.
Расчет магнитных цепей
Теперь внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи — силу тока. Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.
Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.
Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.
Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:
В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.
Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.
Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:
-
Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;
-
Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;
-
После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;
-
Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).
Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.
А примеры расчетов будут?
Здесь — нет. А по ссылке — да! В данном документе Самарского государственного технического университета рассмотрены базовые примеры, которые позволят лучше разобраться в теме, если она вас заинтересовала. Помимо всего прочего, там же приведены теоретические справки. Советую прочитать в надежде, что вы сможете для себя что-то новое подчерпнуть.
Заключение
Во-первых, спасибо, что дочитали статью! Один из способов поддержать меня как автора — подписаться на мой паблик Вконтакте, где иногда выходят «локальные статьи».
Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны…
Произведение магнитной индукции на величину площадки, перпендикулярной направлению поля, называется магнитным потоком через данную площадку.
Магнитный поток через площадку можно рассматривать как совокупность магнитных линий, пронизывающих всю площадку, расположенную перпендикулярно направлению магнитного поля.
Магнитный поток обозначается буквой Ф и вычисляется по формуле: Ф = B * S, где В — магнитная индукция; S — площадь площадки.
В качестве единицы магнитного потока принят вебер (обозначение вб).
Магнитную индукцию можно представить произведением двух сомножителей, один из которых μ — магнитная проницаемость, зависит от физических свойств тела, а второй H — напряженность магнитного поля от величины и расположения электрических токов, создающих это поле, B = μ * H.
Количественная связь между электрическим током и напряженностью окружающего его магнитного поля определяется законом полного тока.
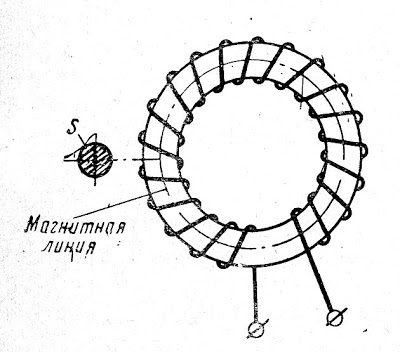
Рассмотрим магнитное поле, образованное кольцевой катушкой, имеющей w витков, равномерно распределенных по всей длине сердечника (рис. 1).
Проведем замкнутый контур, совпадающий с магнитной линией в сердечнике. Поверхность, ограниченная этим контуром, пронизывается w витками. В каждом витке течет ток, равный I.
Полный ток, пронизывающий контур, равен произведению силы тока на число витков.
Вследствие осевой симметрии катушки напряженность поля во всех точках контура имеет одинаковое значение.
В этом случае закон полного тока выражается следующими соотношениями:
где l — длина всего замкнутого контура.
Произведение напряженности магнитного поля на всю длину замкнутого контура, совпадающего с магнитной линией, равно полному току, пронизывающему контур.
Напряженность магнитного поля измеряется в амперах на метр (обозначение а/м).
Закон полного тока лежит в основе расчетов магнитных цепей электрических машин.
Магнитная проницаемость определяется формулой:
Тела, у которых μ меньше единицы (например, медь), называются диамагнитными.
Тела, у которых μ больше единицы (например, воздух), называются парамагнитными.
Магнитная проницаемость диамагнитных и парамагнитных веществ очень близка к единице.
Особую группу составляют так называемые ферромагнитные вещества. Основными ее представителями являются железо, никель, кобальт и их сплавы.
Магнитная проницаемость ферромагнитных тел очень велика, поэтому все электромагниты снабжаются сердечниками из ферромагнитных материалов. При незначительном токе в обмотках в таких сердечниках возникают весьма большие магнитные потоки.
Рис. 1
Рис. 2
Характерным признаком ферромагнитных тел является зависимость их магнитной проницаемости от магнитной индукции и от предыдущих магнитных состояний тела.
Таким образом, магнитная проницаемость ферромагнитных тел является величиной непостоянной и изменяется в зависимости от магнитной индукции.
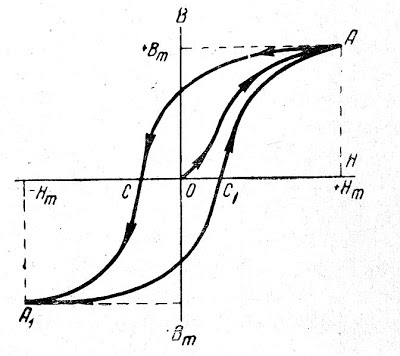
Следовательно, в формуле B = μ * H одновременно с Н изменяется В и μ. Поэтому для того, чтобы характеризовать магнитные свойства ферромагнитных тел, выражают зависимость между В и H графически в виде кривой. На представленном графике (рис. 2) по горизонтальной оси, называемой осью абсцисс, отложены значения напряженности поля в стали, а по вертикальной, называемой осью ординат, — соответствующие величины магнитной индукции в той же стали. Такую кривую называют кривой намагничивания.
Кривые намагничивания стали (железа) впервые были определены в 1871 г. знаменитым русским физиком А. Г. Столетовым.
При рассмотрении кривых намагничивания стали можно установить, что с увеличением напряженности магнитного поля H магнитная индукция В в железе вначале сильно возрастает, а затем приближается к максимальному значению и при дальнейшем увеличении H увеличивается незначительно, или, как говорят, достигает насыщения.
Большое значение для практических целей имеет построение графической зависимости В от H при так называемом циклическом намагничивании железа, т. е. при изменении величины H от нуля до некоторого максимального значения и уменьшении H до нуля, затем изменении направления H и увеличении H до максимального значения, уменьшении H до нуля и увеличении H до максимального значения в первом направлении и т. д. (см. рис. 2).
Полученная замкнутая кривая АСА1С1А называется гистерезисной петлей. Гистерезисом называют отставание В от H в процессе намагничивания и размагничивания.
Теоретически доказано, что площадь, охватываемая гистерезисной петлей, пропорциональна электрической энергии, расходуемой на нагревание железа при его перемагничивании за один цикл. Потери энергии в электрических машинах и аппаратах, связанные с перемагничиванием, называются потерями на гистерезис.
Каждый сорт стали имеет свои кривые намагничивания, определяющие его магнитные свойства.
Определим величину магнитного потока Ф в кольцевой катушке (длина магнитопровода которой равна l, сечение магнитопровода S, магнитная проницаемость его материала μ), имеющей w витков, при прохождении по ней тока l.
Содержание:
- Определение и формула напряженности магнитного поля
- Закон Био-Савара-Лапласа
- Единицы измерения
- Примеры решения задач
Определение и формула напряженности магнитного поля
Определение
Напряженностью магнитного поля $bar{H}$ называют
векторную физическую величину, направленную по касательной к силовым линиям поля, являющуюся характеристикой магнитного поля, равную:
$$bar{H}=frac{bar{B}}{mu_{0}}-bar{J}(1)$$
где $bar{B}$ – вектор магнитной индукции,
$mu_{0}=4 pi cdot 10^{-7}$ Гн/м(Н/А2)- магнитная постоянная,
$bar{j}$ – вектор намагниченности среды в исследуемой точке поля.
Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:
$$bar{H}=frac{bar{B}}{mu_{0}}$$
В изотропной среде формула (1) преобразуется к виду:
$$bar{H}=frac{bar{B}}{mu_{0} mu}$$
где $mu$ – скалярная величина, называемая
относительной магнитной проницаемостью среды (или просто магнитной проницаемостью). В изотропной среде векторы напряженности
магнитного поля и магнитной индукции совпадают по направлению.
Иногда напряженность магнитного поля $d bar{H}$ определяют как
векторную величину, направленную по касательной к силовой линии поля, по модулю равной отношению силы (dF), с которой поле
воздействует на единичный элемент тока (dl), который расположен перпендикулярно полю в вакууме, к магнитной постоянной:
$$d H=frac{d F}{mu_{0} I d l}$$
Закон Био-Савара-Лапласа
Это важнейший в электромагнетизме закон. Он определяет вектор напряженности $d bar{H}$
в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(5)$$
где $d bar{l}$ – вектор элемента проводника, который по модулю равен длине
проводника, направление совпадает с направлением тока; $bar{r}$ – радиус–вектор,
который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля;
$r=|bar{r}|$ .
Вектор $d bar{H}$ – перпендикулярен плоскости, в которой находятся
векторы $d bar{l}$ и
$bar{r}$, и направлен так, что из его конца вращение вектора
$d bar{l}$ по кратчайшему пути до совмещения с вектором
$bar{r}$ происходило по часовой стрелке. Для нахождения направления вектора
$d bar{H}$ можно использовать правило буравчика (Буравчик (винт) вращаем так,
чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением
вектора напряженности поля, которое создает рассматриваемый ток).
Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.
Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует
векторно суммировать все элементарные напряженности $d bar{H}$, порождаемые
элементами проводника и найденные по формуле (4).
Единицы измерения
Основной единицей измерения момента силы в системе СИ является: [H]=А/м
Примеры решения задач
Пример
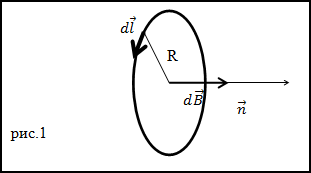
Задание. Чему равна напряженность (H) в центре кругового витка (R — радиус витка) с током I.
Решение. Каждый элементарный ток витка магнитное поле в центре окружности, напряженность которого направлена по
положительной нормали к плоскости контура витка (рис.1). Поэтому, если элементарную напряженность поля найти по закону Био-Савара –
Лапласа, то векторное сложение элементарных полей можно будет заменить на алгебраическое.
В соответствии с законом Био-Савара – Лапласа dH равно:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(1.1)$$
Применяя выражение (1.1) к нашему случаю, получим:
$$d H=frac{1}{4 pi} frac{I d l}{R^{2}}(1.2)$$
Возьмем интеграл по контуру, получим:
$$H=oint_{L} frac{1}{4 pi} frac{I d l}{R^{2}}=frac{1}{4 pi} I cdot frac{2 pi R}{R^{2}}=frac{I}{2 R}$$
Ответ. $H=frac{I}{2 R}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
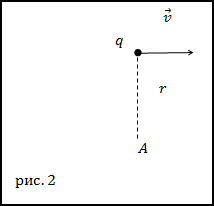
Задание. Какова напряженность магнитного поля, которую создает электрон, движущийся прямолинейно и равномерно со
скоростью v? Если точка, в которой исследуется поле, находится на расстоянии r от электрона на перпендикуляре к вектору скорости,
если перпендикуляр провести через мгновенное положение частицы.
Решение. Сделаем рисунок.
Напряженность магнитного поля будем искать, применяя закон Био – Савара – Лапласа:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(2.1)$$
Учтем, что:
$$I d l=S j d l(2.2)$$
Если все заряды одинаковы (q), то плотность тока равна:
$$bar{j}=q n bar{v}(2.3)$$
заряд отрицательный, следовательно, направления векторов
$bar{j}$ и
$bar{v}$ противоположны. n – концентрация зарядов. Подставим формулу (2.3)
в (2.2), результат в (2.1) получаем:
$$d bar{H}=frac{1}{4 pi} frac{S q n d l}{r^{3}} bar{v} times bar{r}(2.4)$$
где dN=Sdln — количество заряженных частиц в отрезке dl. В таком случае, напряженность поля, которое создает один заряд:
$$bar{H}=frac{d bar{H}}{d N}=frac{1}{4 pi} frac{q}{r^{3}} bar{v} times bar{r}(2.4)$$
По условию задачи $bar{v} perp bar{r}$ , значит модуль напряжённости магнитного поля в точке А (рис.2) будет равен:
$$H=frac{1}{4 pi} frac{q v}{r^{2}}$$
Ответ. $H=frac{1}{4 pi} frac{q v}{r^{2}}$
Читать дальше: Формула напряженности электрического поля.
Магнитным
потоком
(или потоком вектора магнитной индукции
через данную поверхность Sм)
называют произведение магнитной индукции
В
на площадь поверхности Sм
поля:
|
|
(6.2) |
Единица
магнитного потока: [Ф]
= [B][S]
= Tлм2
= Вб (вебер).
Согласно
закону Гаусса для магнитного поля полный
магнитный поток
через замкнутую поверхность равен нулю,
т. е.
.
В
ряде случаев, например, при протекании
тока в катушке, магнитный поток несколько
раз сцепляется с витками катушки. В
первом приближении можно считать, что
все линии магнитной индукции сцепляются
со всеми витками w
катушки.
Тогда потокосцепление
катушки связывается с потоком Ф
простым соотношением: =
wФ.
6.1.5. Напряжённость магнитного поля
Напряжённость
магнитного поля
—
векторная
величина, равная геометрической разности
магнитной индукции
,
делённой на магнитную постоянную, и
намагниченности
вещества,
т. е.
Физический
смысл вектора
определяется
законом Био-Савара: элемент
тока
создаёт
в точке, находящейся на расстоянии
от
элемента тока
(рис.
6.2), магнитное поле с напряжённостью
.
Единица
напряжённости магнитного поля
(ампер
на метр).
Зависимость
от
принято
записывать в виде
|
|
(6.3) |
где0
= 410-7
Гн/м —
магнитная
постоянная,
магнитная проницаемость пустоты; a
= 0[Гн/м]
— абсолютная
магнитная проницаемость
среды (вещества);
= a
/0
— безразмерная относительная
магнитная проницаемость
вещества, показывающая, во сколько раз
магнитная проницаемость среды (вещества)
больше (меньше) магнитной проницаемости
пустоты.
В
зависимости от значения
различают: диамагнетики
с магнитной проницаемостью
< 1
(например, серебро, медь висмут; они
незначительно ослабляют магнитное
поле),
парамагнетики
с
>
1 (например, платина, алюминий, воздух;
магнитное поле в них лишь незначительно
возрастает) и ферромагнетики с магнитной
проницаемостью
>>
1 (
500…5000).
6.1.6.1. Намагниченность ферромагнетиков
К
ферромагнитным материалам (сокращённо
ферромагнетикам) относят сплавы на
основе железа, никеля, кобальта и других
редкоземельных элементов, их соединения;
сплавы и соединения марганца, хрома, а
также пластические и другие композиции
с включением порошков ферромагнитных
металлов (ферриты).
Свойства
ферромагнитных материалов определяются
значением абсолютной магнитной
проницаемости a
=
/
,
где a
= 0,
а —
относительная магнитная проницаемость
материала. Наиболее распространённые
ферромагнетики – это сплавы на основе
железа с добавками Ni,
Co,
или на основе кобальта (Co)
с крупнозернистой структурой (с
зернами-доменами размером 10-3
нм и объёмом 10-9…10-10
нм3)
и с относительной магнитной проницаемостью
= a/0
=
500…5000 и более.
При
отсутствии магнитного поля самопроизвольная
намагниченность доменов ориентирована
хаотически и результирующее магнитное
поле, образованное намагниченностью
этих доменов, слабое (В
0). Под действием внешнего магнитного
поля наблюдается принудительная
ориентация намагниченности доменов по
направлению внешнего магнитного поля
и усиление результирующего магнитного
потока.
Можно
предположить, что при каком-то большом
внешнем поле ()
получим одинаковую ориентацию
намагниченности всех доменов (или
большинства из них), и дальнейшего
усиления внешнего магнитного потока Ф
и индукции В
= Ф/S
не будет. Это явление называют насыщением
ферромагнитного материала.
Соседние файлы в папке лекции эл и эл
- #
- #
- #
- #
- #
- #
- #
Магнитное поле играет очень большую роль в электротехнике и электронике. Без магнитного поля не функционировали бы герконы, электромагнитные реле, соленоиды, катушки индуктивности, дроссели, трансформаторы, двигатели, динамики, генераторы электрической энергии да и вообще много чего.
Природа магнетизма
Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.
Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.
Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.
Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.
Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).
Магнитные линии и магнитный поток
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.
Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.
Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.
Если приблизить два разноименных полюса, то произойдет притягивание магнитов
Если же приблизить одноименными полюсами, то произойдет их отталкивание
Итак, ниже важные свойства магнитных силовых линий.
- Магнитные линии не поддаются гравитации.
- Никогда не пересекаются между собой.
- Всегда образуют замкнутые петли.
- Имеют определенное направление с севера на юг.
- Чем больше концентрация силовых линий, тем сильнее магнитное поле.
- Слабая концентрация силовых линий указывает на слабое магнитное поле.
Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.
Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?
Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».
В физике формула магнитного потока записывается как
где
Ф — магнитный поток, Вебер
В — плотность магнитного потока, Тесла
а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах
S — площадь, через которую проходит магнитный поток, м2
Что же такое 1 Вебер? Один вебер — это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м2 расположенной перпендикулярно направлению магнитного поля.
Напряженность магнитного поля
Формула напряженности
Слышали ли вы когда-нибудь такое выражение: «напряженность между ними все росла и росла». То есть по сути напряженность — это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой
где
H — напряженность магнитного поля, Ампер/метр
B — плотность магнитного потока, Тесла
μ0 — магнитная постоянная = 4π × 10-7 Генри/метр или если написать по человечески 1,2566 × 10-6 Генри/метр.
PS.
Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так.
где
μ — это относительная магнитная проницаемость.
У разных веществ она разная
Напряженность магнитного поля проводника с током
Итак, имеем какой-либо проводник, по которому течет электрический ток.
Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой
где
H — напряженность магнитного поля, Ампер/метр
I — сила тока, текущая через проводник, Ампер
r — расстояние до точки, в которой измеряется напряженность, метр
Магнитное поле проводника с током
Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.
Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.
Ввинчиваем по часовой стрелке — саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.
Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам — кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.
Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?
Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.
Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.
Соленоид
А что если сделать много-много таких петелек? Взять какую-нибудь круглую бобину, намотать на нее провод и потом убрать бобину. У нас должно получится что-то типа этого.
Если подать постоянное напряжение на такую катушку, магнитные силовые линии будут выглядеть вот так.
Вы только посмотрите, какая бешеная плотность магнитного потока внутри такой катушки! Получается, что от каждой петельки магнитное поле суммируется, что в итоге дает такую плотность магнитного потока. Такую катушку также называют катушкой индуктивности или соленоидом.
Вот также схема, показывающая как магнитные силовые линии складываются в соленоиде.
Плотность магнитного потока зависит от того, какая сила тока проходит через соленоид. Чтобы увеличить плотность магнитного потока, достаточно поверх витков намотать еще больше витков и вставить сердечник из специального материала — феррита.
Если в электрических цепях есть такое понятие, как ЭДС — электродвижущая сила, то и в магнитных цепях есть свой аналог — МДС — магнитодвижущая сила. Магнитодвижущая сила выражается в виде тока, протекающего через катушку из N витков и выражается в Амперах-витках.
где
I — это сила тока в катушке, Амперы
N — количество витков катушки, штуки)
Также советую посмотреть очень простое и интересное видео про магнитное поле.
Похожие статьи по теме «магнитное поле»
Катушка индуктивности
Трансформатор
Электромагнитное реле