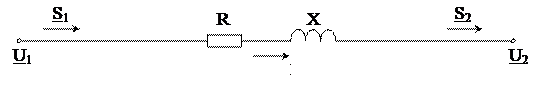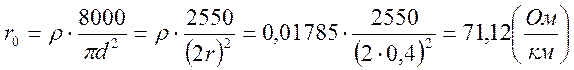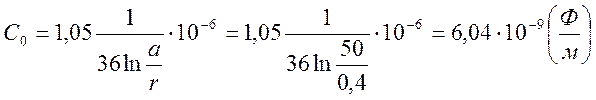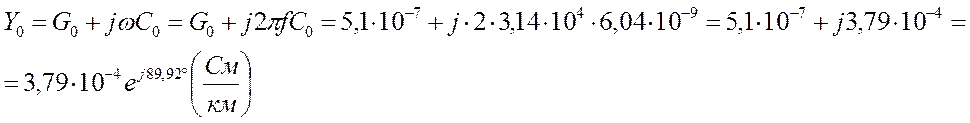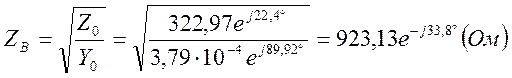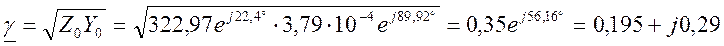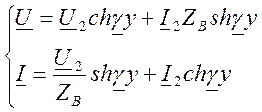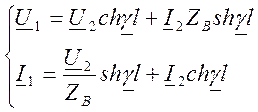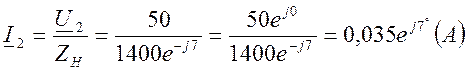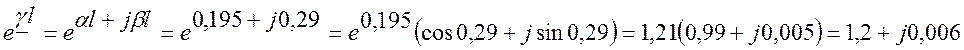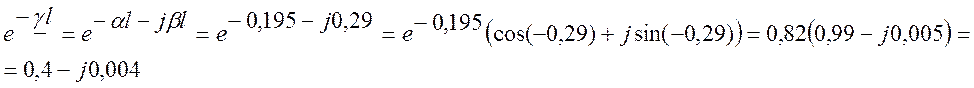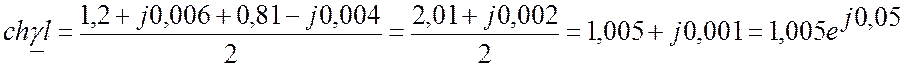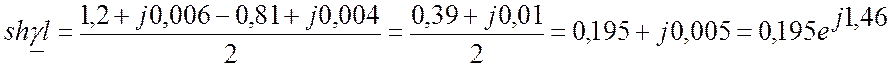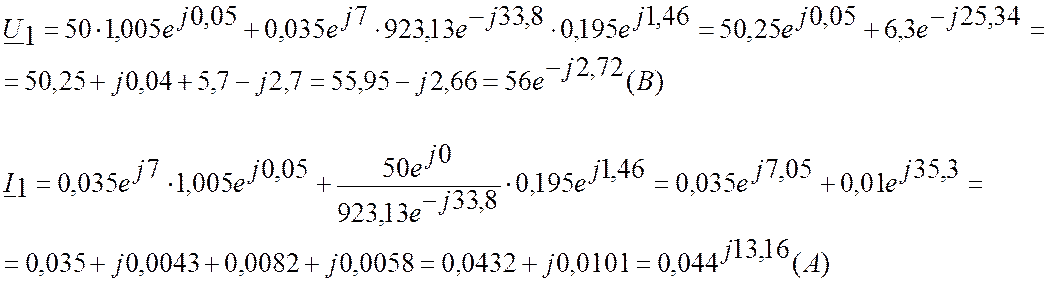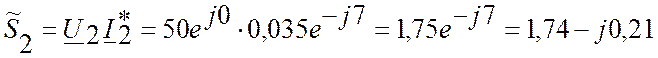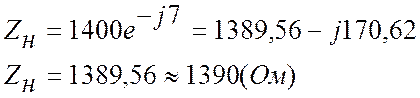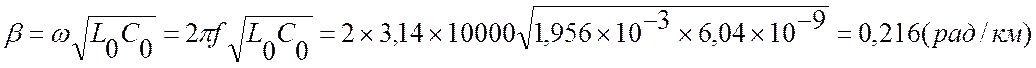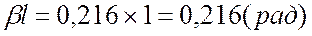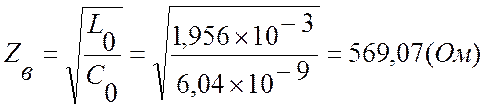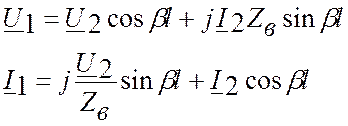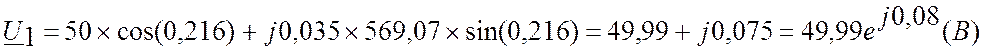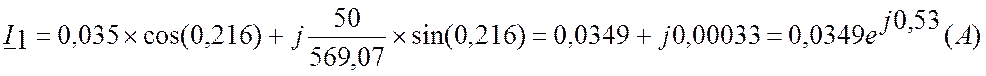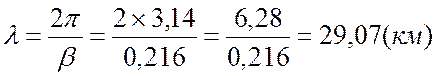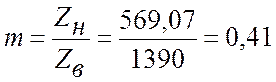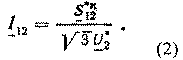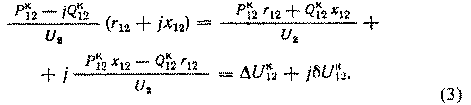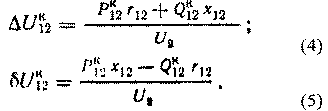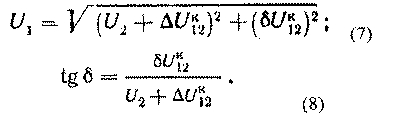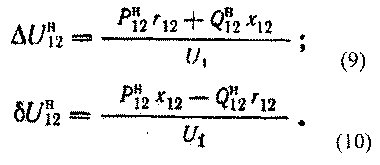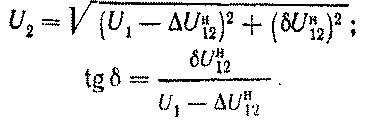Зависимости между напряжениями и мощностями начала и конца элемента электрической сети



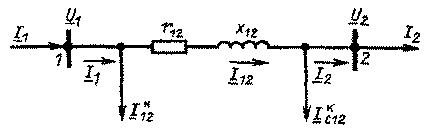
Под элементом электрической сети понимают участок (звено) ее схемы замещения, например, линии электропередачи или трансформатора (рис. 4.3). Так, в случае линии электропередачи звеном будет являться участок ее П-образной схемы замещения между проводимостями. Поскольку в звене сети присутствует только сопротивление Z=R+jX, ток в начале и в конце звена остается неизменным. Расчет будем вести в линейных напряжениях.
Схема замещения элемента электрической сети
Рассмотрим наиболее характерные для практики случаи.
Случай 1 (Расчет по данным конца):известны мощность и напряжение в конце звена: S2=P2 — jQ2; U2. Требуется определить мощность S1 и напряжение U1 в начале.
Этот случай встречается в практике, например, если задана нагрузка потребителя и требуется найти напряжение источника питания, при котором будет обеспечено требуемое напряжение у потребителя.
Потери мощности определим по данным конца звена:
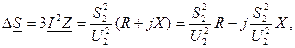
т.е. потери активной мощности:
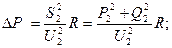
потери реактивной мощности:
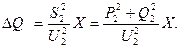
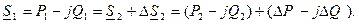
В этом случае потокораспределение находится точно, т.к. мощность и напряжение заданы в одной точке (в конце).
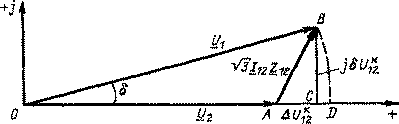
Совмещая вектор напряжения U2 с вещественной осью, запишем:
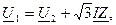
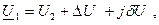
где продольная составляющая падения напряжения:
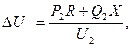
поперечная составляющая падения напряжения:
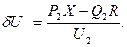
Модуль напряжения в начале звена определяется по выражению (4.15).
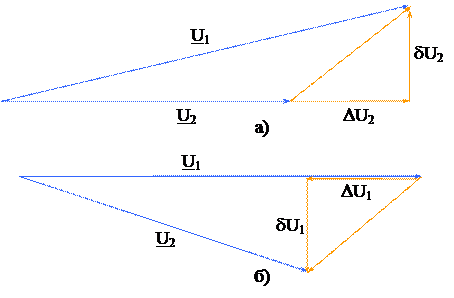
Векторная диаграмма напряжений для этого случая показана на рис. 4.4, а.
Случай 2 (Расчет по данным начала):известны мощность и напряжение в начале звена: S1=P1— jQ1; U1. Требуется определить мощность S2 и напряжение U2 в конце. На практике этот случай имеет место тогда, когда возникает необходимость передачи заданной мощности источника (электростанции) при фиксированном напряжении на его шинах в центр потребления. При этом следует выяснить, каково будет напряжение у потребителей.
Потери мощности, выраженные через параметры начала:
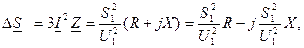
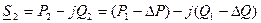
В этом случае потокораспределение также находится точно, т.к. мощность и напряжение заданы в одной точке (в начале).
Совмещая вектор напряжения U1 с вещественной осью, запишем:
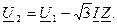
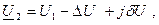
где продольная составляющая падения напряжения:
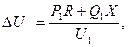
поперечная составляющая падения напряжения:
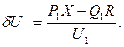
Модуль напряжения в конце звена определяется по выражению (4.16).
Векторная диаграмма напряжений для этого случая показана на рис. 4.4, б.
Векторные диаграммы для звена сети: а – по данным конца; б – по данным начала
Случай 3:известны мощность в конце звена S2=P2 — jQ2 и напряжение в начале U1. Требуется найти мощность в начале звена S1=P1— jQ1 и напряжение в конце U2. Этот случай наиболее типичный, так как обычно известно напряжение на шинах источника питания (электростанции, понижающей подстанции), от которого отходят линии с заданными нагрузками потребителей в конце.
Здесь сразу вычислить напряжение U2 не представляется возможным, так как не известна мощность в начале звена. Поэтому расчет ведут методом последовательных приближений напряжения 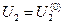
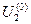
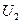
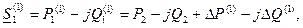
где потери мощности определяют как:
Теперь можно найти первое приближение напряжения:
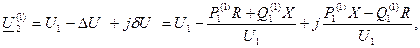
модуль которого подставляют в формулу (4.33) для вычисления потерь мощности и снова находят мощность в начале звена (второе приближение). Расчет заканчивают в том случае, если разность между модулями напряжений U2 i-го и (i-1)-го приближений не больше заданной точности расчета:
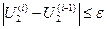
При расчетах без применения ЭВМ обычно ограничиваются расчетом первого приближения напряжения 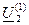
Источник
Вопрос 14 Расчет режима ЛЭП при заданной мощности нагрузки и напряжении в конце линии
Задано напряжение в конце линии U2=сonst. Известна мощность нагрузки S2, напряжение U2, сопротивление и проводимость линии Z12=r12+jx12, в12.
Необходимо определить напряжение U1, мощности в конце и в начале продольной части линии S к 12, S н 12, потери мощности DS12, мощность в начале линии S1. Для проверки ограничений по нагреву иногда определяют ток в линии I12.
Расчет аналогичен расчету при заданном токе нагрузке (I2), и состоит в последовательном определении от конца линии к началу неизвестных мощностей и напряжений при использовании I закона Кирхгофа и закона Ома. Будем использовать мощности трех фаз и линейные напряжения.
Зарядная (емкостная) мощность трех фаз в конце линии:
–jQ к с12=3I *к с12´U2ф=
Мощность в конце продольной части линии по I закону Кирхгофа:
DS12=3I 2 12Z12=
Ток в начале и в конце продольной ветви линии одинаков.
Мощность в начале продольной ветви линии больше, чем мощность в конце, на величину потерь мощности в линии, т.е. S н 12=S к 12+DS12
Линейное напряжение в начале линии по закону Ома равно:
U1=U2+ 
Емкостная мощность в начале линии:
—jQ н c12=
Под влиянием зарядной мощности Qс реактивная мощность нагрузки Q2 в конце, схема замещения уменьшается. Аналогичное явление имеет место и в начале схемы замещения, где реактивная мощность Qс уменьшает реактивную мощность в начале линии.
Это свидетельствует о том, что зарядная мощность сокращает реактивную мощность, поступающую от станции в линию для питания нагрузки. Поэтому зарядная мощность условно может рассматриваться как “генератор” реактивной мощности.
В линии электрической сети имеют место как потери, так и генерация реактивной мощности.
От соотношения потерь и генерации реактивной мощности зависит различие между реактивными мощностями в начале и конце линии.
Вопрос 15 Расчет режима ЛЭП при заданной мощности нагрузки и напряжении в начале линии
Задано напряжение в начале линии.
Т.к. U2 неизвестно, то невозможно определить последовательно от конца линии к началу определить неизвестные токи и напряжения по I закону Кирхгофа и закону Ома.
Нелинейное уравнение узловых напряжений для узла 2 имеет вид:
Это уравнение можно решить и найти неизвестное напряжение U2, а затем найти все мощности по выражениям:
Но можно осуществить приближенный расчет в два этапа.
Предположим, что U2=Uном (7) и определим потоки и потери мощности аналогично выражениям (1)-(4), используя (7) получим:
Определим напряжение U2 по закону Ома, используя поток мощности S н 12, найденный на 1 этапе. Для этого используем закон Ома в виде:

Потоки мощности на 1 этапе определены приближенно, поскольку в формулах вместо U2 использовали Uном.
Соответственно напряжение U2 на 2 этапе также определено приближенно, т.к. в последней формуле для U2 используется приближенное значение S н 12, определенное на 1 этапе.
Возможно итерационное повторение расчета, т.е. повторение 1-го и 2-го этапов для получения более точных значений мощности и напряжений. При проведении расчетов вручную, а не на ЭВМ, такое уточнение не требуется.
Источник
Определение первичных параметров линии. Определение напряжения U1, тока I1, мощности в начале и конце линии, КПД линии
Страницы работы
Содержание работы
Исходные данные (16 вариант):
l = 1 км Zн = 1400e — j 7º Ом
1. Определяем первичные параметры линии:
— сопротивление проводов двухпроводной медной линии на постоянном токе:
ρ – удельное сопротивление проводов при t=20º; для меди ρ=0,01785 Ом*мм 2 /м;
— поправочный коэффициент F(x), учитывающий увеличение активного сопротив ления за счёт поверхностного эффекта:
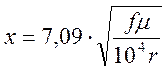
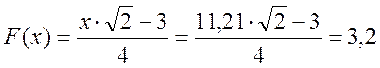
Индуктивность двухпроводной линии
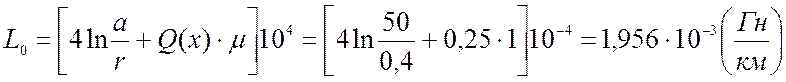
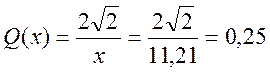
Ёмкость двухпроводной воздушной линии на единицу длины:
Проводимость единицы длины линии:
G0=G’+nf=1×10 -8 +5×10 -11 ×10 4 =5,1×10 -7 (См/км), где
G’ – проводимость изоляции на постоянном токе, равная 1×10 -8 (См/км) при сухой погоде.
n – коэффициент диэлектрических потерь, равный 5×10 -11 (См/км×Гц) при сухой погоде.
2. Определяем напряжение U1, ток I1, мощности в начале и конце линии, КПД линии
а) Определяем вторичные параметры линии:
— полное комплексное сопротивление единицы длины линии:
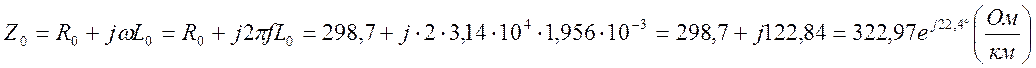
— волновое сопротивление линии:
— комплексный коэффициент распространения:
γl = αl+jβl = (0,195+j0,29)×1 = 0,195+j0,29
затухание сигнала αl = 0,195 (Нп)
изменение фазы βl = 0,29 (рад)
б) Запишем уравнения для линии с потерями через параметры конца линии:
Для расчёта напряжения и тока в начале линии U1и I1 вместо y подставляем l, тогда:
Так как ток I2 в конце линии неизвестен, но известны нагрузка и напряжение в конце линии, то найдём его:
Рассчитываем 
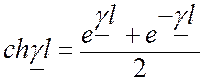
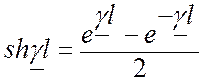
в) Рассчитаем полную комплексную мощность в начале и конце линии и КПД линии
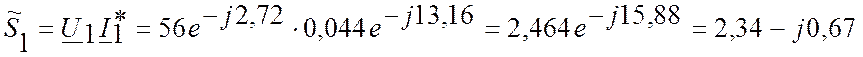
Полная мощность S1=2,464 (BA)
Активная мощность P1=2,34 (Вт)
Реактивная мощность Q1=-0,67 (вар)
Активная мощность P2=1,74 (Вт)
Реактивная мощность Q2=-0,21 (вар)
3. Для линии без потерь определяем напряжение U1 и ток I1 в начале линии, а также длину электромагнитной волны λ:
а) Для линии без потерь R0=0, G0=0
Определяем изменение фазы сигнала по всей длине линии
Определяем волновое сопротивление
б) Напряжение и ток в начале линии без потерь
Длина электромагнитной волны λ:
4. Построим график U=f(βy) для линии без потерь:
Источник
Для
определения напряжение в конце передачи
рассматривается уравнение четырехполюсника:
, (4.1)
где
и
— приведенные к высшей (входной) стороне
напряжение и ток в конце передачи.
Напряжение
в начале передачи задано по абсолютной
величине как в максимальном, так и в
минимальном режимах. Приведенное
приближенное значение токаобеих цепей можно определить по
номинальному напряжению высшей стороны
и заданной мощности нагрузки:
. (4.2)
Известен
также угол между
и
,
который является углом сопротивления
нагрузки на шинах С (рис. 8), т. е.:
. (4.3)
Обобщенные
постоянные
и
передачи по величине и фазе были
определены при решении п. 3.3. Таким
образом, в уравнении четырехполюсника
неизвестны напряжение в конце линиипо величине и углу, а также угол между
и
.
Эта задача может быть решена графически:
1)
направляем ток
по вещественной оси (рис. 5);
2)
определяем угол нагрузки
;
3)
под углом
наносим линию направления
,
величинапока не известна;
4)
определяем
(угол
)
по фактическому значениюсогласно (3.24);
5)
под углом
наносим вектор
(отрезокOm);
6)
аналогично находим
(угол
);
7)
под углом
наносим направление вектора
.
Вектореще не определен, поэтому можно найти
только его направление;

от конца вектора
(точкаm)
наносим прямую, параллельную
;
9)
так как
известно по величине, от точки O циркулем
делаем засечку радиусом, равным величине.
Получаем треугольникOmn.
Вектор
состоит из суммы двух векторов —
и
.
Тогда(отрезокOn)
будет третьей стороной треугольника
Omn;
10)
абсолютное значение
можно определить делением абсолютных
значений:/
.
Такая
диаграмма строится как для максимального,
так и для минимального режимов. При этом
для максимального режима используются
(
)
и,
а для минимального режима —(
)
и(в режиме
).
Зная
абсолютные значения напряжений в начале
и в конце
линии, можно определить потерю напряжения
для любого режима. Наибольшую потерю
напряжения в большинстве случаев дает
максимальный режим, т. е.:
. (4.4)
5. Определение коэффициентов трансформации
Требуемые
коэффициенты трансформации по условиям
стабильности напряжения у потребителя
с учетом заданных отклонений будут
различными в разных режимах:
,
. (5.1)
Если
согласно рассматриваемому примеру
напряжение на шинах С в конце передачи
,
то в максимальном и минимальном режимах
соответственно:
; (5.2)
Регулирование
напряжения заключается в следующем:
при изменении режимов коэффициенты
трансформации меняются так, чтобы
обеспечить диапазон отклонений напряжения
на шинах С согласно заданию (±2 %).
Для
фазных величин это выразится неравенством:
. (5.3)
Выбор
ответвлений у трансформаторов производится
так, чтобы обеспечить напряжение у
потребителей согласно выражению
(5.3). Следовательно, ответвление на
подстанции В (ответвления, как правило,
делаются на стороне высшего напряжения
трансформаторов) в максимальном режиме
должно быть равно или меньше напряжения
,
а в минимальном — равно или больше
напряжения.
При
изменении режима регулятор переключает
ответвления в этих пределах. Следует
проверить наличие приемлемых ответвлений
у выбранного трансформатора.
Соседние файлы в папке ПЭТУ1
- #
25.03.201658.27 Кб5Data009.tif
- #
25.03.201649.08 Кб3Data010.tif
- #
25.03.201665.6 Кб3Data011.tif
- #
- #
25.03.201631.74 Кб3исходные_данные.xls
- #
- #
- #
- #
Страницы работы
Содержание работы
Исходные данные (16 вариант):
f = 10 кГц U2 = 50 В
l = 1 км Zн = 1400e—j7º Ом
a = 50 мм Тип
– ВЛ
r = 0,4 мм
1. Определяем первичные параметры
линии:
— сопротивление проводов двухпроводной
медной линии на постоянном токе:
ρ – удельное сопротивление
проводов при t=20º; для меди ρ=0,01785 Ом*мм2/м;
— поправочный коэффициент F(x), учитывающий увеличение активного сопротив ления за счёт
поверхностного эффекта:
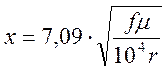
для меди µ=1; 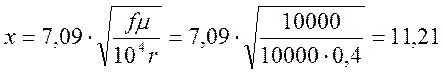
По таблице определяем F(x):
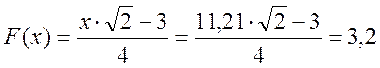
R0=r0(1+F(x))=71,12(1+3,2)=298,7
(Ом/км)
Индуктивность двухпроводной линии
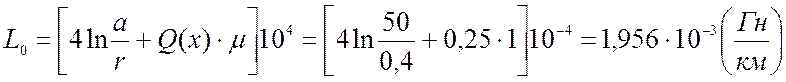
;
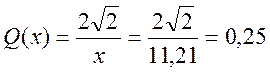
Ёмкость двухпроводной воздушной линии
на единицу длины:
Проводимость единицы длины линии:
G0=G’+nf=1×10-8+5×10-11×104=5,1×10-7
(См/км), где
G’ – проводимость изоляции
на постоянном токе, равная 1×10-8 (См/км) при
сухой погоде.
n – коэффициент диэлектрических
потерь, равный 5×10-11 (См/км×Гц) при сухой
погоде.
2. Определяем напряжение U1, ток I1,
мощности в начале и конце линии, КПД линии
а) Определяем вторичные параметры
линии:
— полное комплексное сопротивление
единицы длины линии:
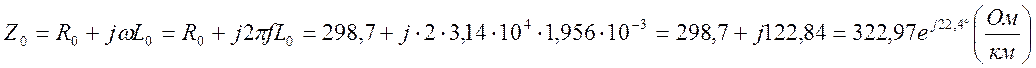
полная комплексная проводимость единицы длины линии:
— волновое сопротивление линии:
— комплексный коэффициент распространения:
γl = αl+jβl = (0,195+j0,29)×1 = 0,195+j0,29
затухание сигнала αl = 0,195 (Нп)
изменение фазы βl = 0,29 (рад)
б) Запишем уравнения для линии с
потерями через параметры конца линии:
Для расчёта напряжения и тока в
начале линии U1и I1 вместо y подставляем l,
тогда:
Так как ток I2 в конце линии неизвестен, но известны нагрузка и
напряжение в конце линии, то найдём его:
Рассчитываем и
, для этого воспользуемся следующими соотношениями:
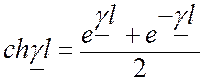
; 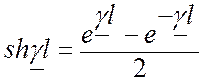
Рассчитаем U1 и I1 в начале
линии:
в) Рассчитаем полную комплексную
мощность в начале и конце линии и КПД линии
Полная мощность S1=2,464 (BA)
Активная мощность P1=2,34
(Вт)
Реактивная мощность Q1=-0,67
(вар)
Полная мощность S2=1,75
(BA)
Активная мощность P2=1,74
(Вт)
Реактивная мощность Q2=-0,21
(вар)
Определяем КПД линии:
η=(Р1/Р2)×100%=(1,74/2,34)×100%=74,36%
3. Для линии без потерь определяем
напряжение U1 и ток I1
в начале линии, а также длину электромагнитной волны λ:
а) Для линии без потерь R0=0,
G0=0
Нагрузка стала активной
Коэффициент фазы
Определяем изменение фазы сигнала по
всей длине линии
Определяем волновое сопротивление
б) Напряжение и ток в начале линии
без потерь
тогда
Длина электромагнитной волны λ:
4. Построим график U=f(βy) для линии без потерь:
|
|
0 |
|
|
2,16 |
|
|
0 |
3,634 |
7,258 |
1 |
|
|
1 |
|
0 |
0,976 |
|
|
1 |
0,5 |
0 |
0,952 |
|
|
0 |
|
1 |
0,214 |
|
|
0 |
|
1 |
0,0458 |
|
|
0 |
0,084 |
0,1681 |
0,0077 |
|
|
50 |
38,21 |
20,5 |
48,98 |
Похожие материалы
- Определение тока и закона изменения во времени тока во второй ветви, приведённой схемы, интегралом Дюамеля
- Переходные процессы в линейных электрических цепях с сосредоточенными параметрами
- Переходные процессы при заряде и разряде конденсатора
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
ПОТЕРИ НАПРЯЖЕНИЯ. ПАДЕНИЕ НАПРЯЖЕНИЯ
На рис. 1 приведена схема замещения линии
электропередач, а на рис. 2 векторная диаграмма для линейных напряжений в начале
и в конце этой линии.
Рис. 1. Схема замещения линии
электропередач
Рис. 2. Векторная диаграмма напряжений в
начале и в конце линии при
расчете по данным конца
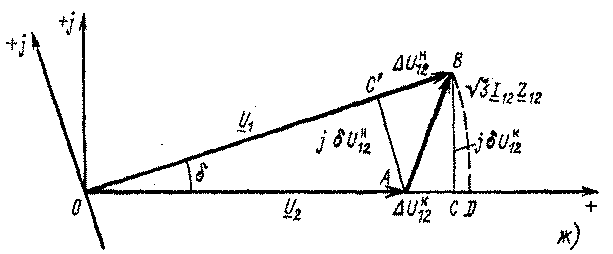
Падение напряжения —
геометрическая (векторная) разность между комплексами напряжений начала и конца
линии. На рис. 2 падение напряжения — это вектор
Продольной составляющей падения
напряжения AU12 называют проекцию падения напряжения на
действительную ось или на напряжение Ό?, AU12К
= AC на рис. 2.
Индекс «к» означает, что AU]2K
— проекция на напряжение конца линии U2. Обычно
AUJ2K выражается через данные в конце линии:
U2, Р12К, QnK—
Поперечная составляющая падения
напряжения SU12К — это проекция падения напряжения
на мнимую ось, SU12К — CB на рис. 2. Таким
образом,
Часто используют понятие потеря
напряжения — это алгебраическая разность между модулями напряжений
начала и конца линии. На рис, 2
U1 — U2 =
AD. Если поперечная составляющая SUj2к мала
(например, в сетях UhomS ПО кВ), то можно приближенно
считать, что потеря напряжения равна продольной составляющей падения напряжения.
Расчет режимов электрических сетей
ведется в мощностях, поэтому выразим падение напряжения и его составляющие через
потоки мощности в линии.
Известны мощность и напряжение в
конце линии (расчет напряжения в начале линии по данным конца). Выразим ток
в линии I12 в (1) через мощность в конце продольной
части линии S12K и напряжение U2.
В результате получим
Приравняв в (3) действительные и мнимые
части, получим выражения продольной и поперечной составляющих падения напряжения
по данным конца:
Напряжение в начале линии
где U2известно;
AU12K, SU2К
определяем из (4) и (5). Соответственно модуль и фаза напряжения в начале линии
(см. рис.2)
Известны мощность и напряжение в начале
линии (расчет напряжения в конце линии по данным начала). Направим U1
по действительной оси, т. е. примем, что U1-U
(рис. 3).
На рис. 3 изменилось
положение осей в сравнении с рис. 2. Продольная
TT
составляющая падения напряжения
AU12 = ВС — это проекция падения напряжения на действительную
ось или на Uj. Поперечная составляющая падения напряжения 5U12Н
= AC — это проекция падения напряжения на мнимую ось. Один и тот же
вектор падения напряжения AB проектируется на различные оси.
Рис. 3. Векторная диаграмма напряжений в
начале и в конце линии при
расчете по данным начала
Поэтому
Если выразить ток в линии I12
аналогично (2) через известные в данном случае мощность в начале
продольной ветви линии S12H и U1,
то получим выражения, аналогичные (4) и (5)
Напряжение в конце линии
где U1 известно;
AU12«, SU12» определяются из (9), (10).
Модуль и фазг U2 равны
В начало