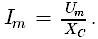Как работает конденсатор и катушка в цепи переменного тока
Содержание
- 1 Особенности работы конденсатора
- 2 Формула ёмкости
- 3 Особенности электроцепи с емкостью и индуктивностью
- 4 Виды конденсаторов
- 5 Различные характеристики конденсаторов
- 6 Где используются конденсаторы
- 7 Видео по теме
Работа многих электрических схем строится на использовании конденсаторов. Основной особенностью этих радиоэлементов является то, что они хорошо проводят переменный ток, но не пропускают постоянный.
Особенности работы конденсатора
Радиодеталь представляет собой две пластины, к которым прикреплены металлические выводы. Пластины не соприкасаются между собой. Обычно между ними проложен слой изолятора. Постоянный электроток через конденсатор проходить не может, так как нет контакта между проводниками, но для переменного он не является препятствием.
Когда конденсатор включен в цепь переменного тока, частота напряжения меняется по закону синусоиды. Сначала электродвижущая сила растёт до своего максимума. После этого она уменьшается до нуля, а затем переходит в отрицательную область, где постепенно возрастает до амплитуды, взятой со знаком минус. Затем отрицательная ЭДС уменьшается по абсолютной величине до нуля и начинает возрастать в положительной области до наибольшего значения. Описанный цикл изменений повторяется снова и снова.
Когда конденсатор работает в цепи переменного тока, в нем циклически происходят следующие процессы:
- При возрастании амплитуды от нулевого значения до максимального происходит накопление заряда. Пластины накапливают равные по абсолютной величине, но противоположные по знаку заряды.
- При уменьшении до нуля накопление прекращается, заряд уменьшается, так как начинает стекать с пластин конденсатора.
- Когда напряжение меняется на противоположное, на пластины начинают поступать заряды, которые имеют знаки, противоположные тем, что были раньше.
- Как только ЭДС достигнет максимального отрицательного значения и станет уменьшаться по абсолютной величине, начнётся разрядка конденсатора.
Описанный здесь цикл повторится с началом возрастания ЭДС. Он будет осуществляться до тех пор, пока переменный ток не будет отключён.
Формула ёмкости
Одна из самых важных характеристик конденсатора — ёмкость. Её обозначают символом C. Несмотря на то, что контакта между пластинами нет, ток будет идти через конденсатор в цепи переменного тока то к пластинам, то от них. Это обусловлено циклически происходящими процессами зарядки и разрядки конденсатора.
Величина ёмкости характеризует способность конденсатора накапливать заряд при поступлении на обкладки определённой разности потенциалов. Ее можно найти по формуле:
Используя эту формулу наряду с законом изменения напряжения, можно узнать силу тока, возникающего в процессе зарядки или разрядки пластин конденсатора в цепи переменного тока. Но для этого необходимо сделать соответствующие преобразования.
Сначала находим напряжение, возникающее на конденсаторе в цепи переменного тока, воспользовавшись формулами для определения ёмкости и разности потенциалов. После преобразований получаем выражение:
Из него находим величину заряда:
Теперь можно получить выражение для электротока в цепи с конденсатором:
Надо сказать, что при выводе формулы для нахождения силы электрического тока были использованы следующие приемы:
- От выражения для заряда была взята производная по времени.
- Затем было выполнено эквивалентное тригонометрическое преобразование.
- Um соответствует максимальному значению амплитуды колебаний электронапряжения.
Полученное выражение позволяет узнать ток зарядки и разрядки конденсатора в любой момент. Изменения тока опережают напряжение на половину «пи». Величина тока будет максимальной при нулевом напряжении. И, наоборот, значение тока станет нулевым, когда напряжение достигнет максимума.
Для определения ёмкости может быть использована еще такая формула:
Как видно из формулы, ёмкость конденсатора увеличивается при увеличении площади пластин и уменьшении расстояния между ними.
Емкостное сопротивление — ещё одна важная характеристика конденсатора. Его можно найти по формуле:
Если взять формулу для определения амплитуды электротока:
И подставить в нее значение ХС, то получим:
После изучения данной формулы становится понятно, что емкостное и активное сопротивление из закона Ома играют одну и ту же роль. Поэтому емкостное можно считать сопротивлением конденсатора переменному электротоку.
Пример использования формул для решения простых задач по нахождению емкости конденсатора можно увидеть на изображении ниже:
Особенности электроцепи с емкостью и индуктивностью
Рассматривая ранее цепь переменного тока с включенным конденсатором, мы могли видеть, что частота колебаний электротока на конденсаторе опережает частоту колебаний электронапряжения на π/2. При включении катушки индуктивности наблюдается обратное явление, то есть, электроток отстает от электронапряжения на π/2. Его амплитуда определяется по формуле:
Знаменатель в данной формуле представляет собой выражение, используемое для определения индуктивного сопротивления:
В итоге получаем формулу для силы электротока:
Индуктивное сопротивление, как и емкостное, зависит от частоты электротока. Поэтому катушка, включенная в постоянную цепь, будет иметь нулевое индуктивное сопротивление.
Конденсатор и катушка индуктивности в цепи переменного тока образуют, так называемый, колебательный контур. Его колебания определяются по формуле:
При вынужденных колебаниях сила элетротока достигает максимума, если колебания электронапряжения и самого контура становятся равными:
Виды конденсаторов
На данный момент существует огромный выбор конденсаторов:
- Наиболее распространены радиодетали с двумя обкладками, но их может быть и больше.
- Плоский конденсатор состоит из двух пластин, между которыми расположен тонкий слой диэлектрика. Его толщина должна быть небольшой по сравнению с размерами пластин.
- В цилиндрическом конденсаторе обе пластины имеют цилиндрическую форму. Одна из них находится внутри другой. Между цилиндрами имеется равномерный тонкий промежуток, который заполнен диэлектриком.
- Существуют сферические конденсаторы, обкладки которых представляют собой сферы, одна из которых находится внутри другой.
Конденсаторы различаются в зависимости от вида диэлектрика. В частности, может использоваться не только твёрдый, но и жидкий или газообразный диэлектрик. Есть также вакуумные конденсаторы, в которых внутри между обкладками находится вакуум.
Существуют оксидно-полупроводниковые конденсаторы. Один из их электродов является анодом. Диэлектриком выступает покрывающий его оксид. Катодом является полупроводниковый слой, который наносится на слой оксида.
Для изолирующего слоя могут использоваться как органические, так и неорганические материалы. В первом случае применяются бумажные или плёночные материалы. Неорганический диэлектрик выполняется из керамики, стекла, слюды или неорганических синтетических плёнок. Есть и такие, внутри которых содержится электролитический раствор. Конденсаторы с подобным диэлектриком характеризуются относительно высокой ёмкостью.
Еще одна разновидность конденсаторов — подстроечные. Их использование предоставляет возможность изменять значение емкости в определенных пределах, чтобы деталь могла работать наиболее эффективно.
Наряду с конденсаторами общего назначения существуют и те, которые предназначены для специального применения. Примерами таких видов являются дозиметрические, высоковольтные, пусковые, импульсные, помехоподавляющие и некоторые другие радиоэлементы.
Различные характеристики конденсаторов
Основной характеристикой конденсатора является ёмкость. Но при выборе необходимо учитывать и другие.
Для каждого конденсатора существует номинальное напряжение. Если эксплуатация детали будет осуществляться исключительно при таком значении, производитель гарантирует качественную работу в течение всего срока службы.
При увеличении подаваемого на пластины напряжения заряд будет увеличиваться. Если разность потенциалов станет слишком большой, произойдёт пробой радиодетали. В результате между обкладками пройдёт искра, а сам конденсатор станет неисправной. Конденсатор в цепи переменного тока необходимо эксплуатировать в строго заданных параметрах. Иначе срок его эксплуатации существенно сокращается.
Ещё одна характеристика — удельная ёмкость. Она равна отношению ёмкости и массы используемого диэлектрика. С её повышением улучшаются характеристики, но возрастает вероятность пробоя.
В формуле для определения ёмкости используется понятие диэлектрической проницаемости диэлектрика, который находится между пластинами. Эта характеристика определяет то, насколько сильно данное вещество ослабляет влияние электрического поля между обкладками.
В диэлектриках электроны сильно привязаны к ядрам атомов, из-за чего они не перемещаются под действием электрического поля и не образуют электрический ток. Однако при воздействии электрического поля осуществляется поляризация атомов за счет смещения электронов внутри них. Следствием этого является ослабление электрического поля. Его величина зависит от того, какое вещество используется в качестве диэлектрика. Возмущение электрического поля, создаваемое диэлектриком, ослабляет то, которое было приложено к пластинам, и препятствует притоку заряда к пластинам.
Где используются конденсаторы
Радиодетали этого вида находят применение в разных сферах деятельности современного человека:
- Конденсатор и катушка индуктивности в цепи переменного тока образуют колебательный контур, его используют во многих устройствах.
- Конденсаторы меняют свои характеристики в зависимости от температуры или влажности окружающей среды, поэтому применяются в самых разных измерительных приборах.
- Еще одна сфера применения— блоки питания.
- Используются в цепях с преобразователями переменного тока в постоянный.
- Применяются в частотных фильтрах.
- Без конденсатора трудно представить усилитель.
- Конденсатор является важным элементом для процессоров и других микросхем.
Здесь приведены только некоторые варианты использования. На самом деле их гораздо больше.
Видео по теме
Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.
Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем). Заряженный конденсатор для постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен резистору с некоторым вполне определенным сопротивлением (если пока забить забыть про всякие там сдвиги фазы, об этом ниже). Нам надо каким-нибудь образом получить связь между током и напряжением на конденсаторе.
Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор. Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.
Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение
Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt. Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.
Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением
Давайте-ка выразим из этой формулы заряд конденсатора:
А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:
Емкость конденсатора у нас является величиной постоянной. Она определяется исключительно самим конденсатором, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость С конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением U нельзя так поступить! Напряжение на конденсаторе будет изменяться со временем. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него. Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.
А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:
По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.
Рисунок 1 – Поясняющая картинка
На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.
Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения. Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.
Пусть напряжение на конденсаторе емкостью C изменяется по закону синуса вот таким вот образом
Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше. Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную
Или можно записать вот так
Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то . Не понятно, откуда взялось это выражение? Погуглите формулы приведения

Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок. Итак, сейчас мы получили немаловажный вывод – если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов. Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости C конденсатора, амплитуды приложенного к нему напряжения Um и частоты ω. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).
Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе
На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе. По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).
Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t) через конденсатор емкостью C. И закон этот пусть тоже будет синусоидальным
Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:
По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом
Здесь мы снова воспользовались интересными сведениями из тригонометрии, что . И снова формулы приведения придут вам на помощь, если не понятно, почему получилось именно так.
Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов. Более того, они не просто так сдвинуты. Ток опережает напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.
Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.
Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.
Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем.
Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.
Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.
Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото 
Рисунок 3 – Ищем ток через этот конденсатор
Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.
Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону
Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так
Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока
Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало. Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует 
Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.
Рисунок 4 – График напряжения в розетке
Рисунок 5 – График тока через конденсатор
Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть. И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Конденсаторы — это приборы, накапливающие электрическую энергию в виде зарядов. Аппараты не могут пропускать через себя постоянный ток. Будучи включёнными в цепь с переменным током, он уподобляется пружине, подвергающейся внешнему воздействию. Примечательно, что они не будет пропускать и ток, однако при его прохождении случится перезарядка накопителя, из-за чего покажется, что он проходит через обкладки. Если к ним в разряженном состоянии приложить постоянное напряжение, то по цепи пойдет ток, который снижается по мере зарядки накопителя. Когда достигается паритет значений напряжения на источнике питания и пластинах, он прекращает протекать, что приводит к разрыву.
Что такое конденсатор
Конденсаторы — это пассивные элементы, используемые при формировании разнообразных электротехнических схем, блокирующих и защитных устройств. Будучи включённым в переменную цепь накопитель аккумулирует и возвращает энергию. Если подключается переменный, то энергия возвращается в систему, при этом поддерживается периодичность, которая соответствует рабочей частоте.
К сведению! Когда через конденсатор протекает переменный ток, то он непрерывно оказывает ему сопротивление, величина которого обратно пропорционально зависит от частоты.
Уменьшение частоты приводит к повышению сопротивления. Когда источник, генерирующий такой ток, подключается к накопителю, то максимальное напряжение определяется силой.
Чтобы на примере убедиться в возможности проведения переменного тока, формируют простую электрическую цепь, включающую следующие компоненты:
- переменные источники;
- конденсатор;
- потребитель — обычно это лампочка.
Обратите внимание! Прибор не допускает пропускание по постоянной сети, поскольку в этом случае имеющееся сопротивление будет равно бесконечности. Если проходит переменный, то у сопротивления будет конечное значение.
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Вам это будет интересно Устройство и принцип действия амперметра для измерения тока
Принцип работы конденсатора
Подключение прибора к постоянному источнику приводит к тому, что в начальный момент происходит аккумуляция в обкладках из-за электростатической индукции, а сопротивление в этот момент приравнивается нулю. Электрическая индукция провоцирует поле к притяжению разноимённых зарядов на разные обкладки, расположенные друг напротив друга.
Вам это будет интересно Регулятор мощности нагрузки
Такое свойство получило название ёмкость, которая характерна для всех типов материалов, в том числе и диэлектриков, однако в случае с проводниками она существенно больше. Именно поэтому обкладки изготавливаются из проводника. Увеличение ёмкости способствует накоплению большего количества зарядок на обкладках.
Важно! Когда аккумулируются заряды, происходят ослабление поля и наращивание двухполюсника.
Происходит это из-за уменьшения места в обкладках, воздействия одноимённых зарядов друг на друга. Одновременно с этим напряжение приравнивается к источнику тока. Прекращение электричества в цепи происходит после того, когда обкладки полностью заполнятся электричеством. Из-за этого пропадает индукция и остаётся только поле, удерживающее и не пропускающее заряды.
Электротоку будет некуда деться, а на двухполюснике напряжение приравнивается к ЭДС. Когда ЭДС повышается, поле сильнее воздействует на диэлектрик из-за отсутствия места в обкладках. Если внутреннее конденсаторное напряжение будет выше предельных значений, тогда пробьёт диэлектрик.
Конденсатор преобразуется в проводник, и происходит освобождение зарядов, из-за чего электроток начинает идти. Чтобы применять двухполюсник при высоком напряжении повышают размер диэлектрика и наращивают расстояние, имеющееся между обкладками на фоне снижения ёмкости. Диэлектрик располагается между обкладками и не даёт проходить постоянному, выполняя в отношении него барьерную функцию.
Обратите внимание! Именно постоянное напряжение способно формировать электростатическую индукцию, но только в случае замыкания в момент зарядки конденсатора. Благодаря этому механизму сохраняется энергия до момента подсоединения к нему потребителю.
Конденсатор в цепи постоянного тока
Чтобы понять, как работает накопитель в цепи постоянного тока, надо добавить в схему лампочку, которая станет загораться только при зарядке, в процессе которой от электротока остаётся напряжение, как бы догоняющее его из-за плавного нарастания. Заряды электричества затрачивают какое-то время для перемещения к обкладкам, именно это и есть время зарядки, продолжительность которого определяется частотой и ёмкостью напряжения. Когда зарядка завершается, лампочка тухнет, и постоянный электроток перестаёт проходить через пассивный электронный компонент.
Конденсатор в цепи переменного тока
Если у источника изменить полярность, то это приведёт к разрядке конденсатора в цепи переменного тока и его повторной зарядке. Формируется постоянная электростатическая индукция при переменном. Всегда при изменении электричеством своего направления запускается механизм зарядки и разрядки, из-за чего он и пропускает переменный. Увеличение частоты приводит к снижению ёмкостного сопротивления двухполюсника.
Вам это будет интересно Как подключить реле напряжения
Емкостное сопротивление
Если подключить генератор синусоидального сигнала, с помощью осциллографа можно регистрировать увеличение силы тока по мере роста частоты. В ходе эксперимента нужно поддерживать одинаковую амплитуду на входе.
В следующих разделах публикации рассказано о том, почему происходят отмеченные явления.
Понятие ёмкости
Рассмотренная выше схема стандартной конструкции подразумевает влияние следующих параметров на способность накопления определенного заряда (q):
- площади (S) рабочих пластин или обкладок;
- расстояния (d) между этими функциональными компонентами;
- диэлектрических характеристик слоя (e – проницаемость).
Выяснив значения перечисленных величин, можно рассчитать напряженность:
E = q/(e*S).
Накопительные свойства (емкость) определяет следующая формула:
С= (e * S)/ d = q/U, где U – напряжение.
Для случая с переменным током нужно учесть изменение параметров за определенный интервал времени:
I = Δq/Δt.
С учетом представленных выше зависимостей после простых математических преобразований можно создать алгоритм расчета силы тока, который будет проходить по цепи:
I = (C * ΔU)/Δt = f * C * Uo cos f * t = Io * sin (f * t + 90), где f – частота сигнала.
Векторное представление
Для наглядности процессов основные электрические параметры удобно представлять в векторной форме. Чтобы учесть замедление процессов обмена энергией, устанавливают понятие емкостного сопротивления (Xc).
Пояснение общих зависимостей
График и векторное представление демонстрируют отставание напряжения от тока, который будет течь в цепи на 90° (π/2).
К сведению. Обратный эффект наблюдается, если включить в схему катушку индукции. В этом случае напряжение будет опережать ток по фазе на аналогичный угол (90°).
Приведенные особенности подтверждают наличие реактивных компонентов конденсаторов и катушек, соответственно. В упрощенном виде сопротивление Хс выражается обратной зависимостью от частоты и емкости:
Xc = 1/ (f * C).
Представленную формулу можно использовать для расчета фильтров, колебательных контуров и других схем.
График ёмкостного сопротивления
Может ли через конденсатор протекать постоянный ток, отмечено выше. Наличие слоя диэлектрика предотвращает свободное протекание электронов через этот участок. Такой материал только накапливает заряды, но при одинаковых потенциалах эквивалентен разрыву проводника. При работе с переменным сигналом ток смещения в переделах этой зоны выполняет функцию «соединения» цепи.
Выводы:
- отсутствие колебательных процессов (f=0) соответствует уменьшению до нуля проводимости, что аналогично разрыву цепи;
- при увеличении емкости сопротивление конденсатора уменьшается;
- чем выше частота, тем лучше проводимость.
Работа (мощность) в ёмкостной нагрузке
Выше отмечена цикличность энергетического обмена между источником переменного сигнала и подключенным конденсатором.
Диаграммы демонстрируют процессы в конденсаторе на примере сжимания/ растяжения пружины внешней силой. В идеальных условиях энергетические потери отсутствуют. Однако в реальной ситуации нужно учесть потребление мощности активным сопротивлением соединительных проводов, иных компонентов схемы. Уменьшение КПД объясняется ухудшением функционального состояния диэлектрика.
Прочие параметры
Для уточненных расчетов применяют эквивалентную схему изделия со следующими компонентами:
- емкость;
- электрические сопротивления изоляционного слоя, контактных и проводящих элементов конструкции;
- индуктивные реактивные составляющие.
К сведению. После отключения нагрузки на выводах конденсатора фиксируется небольшой рост напряжения (абсорбция заряда). Также существует зависимость рабочих параметров от температуры.
Почему идет переменный ток через конденсатор
Конденсатор — это разрыв, поскольку его прокладки не касаются друг друга из-за нахождения между ними диэлектрика, не проводящего постоянный электроток. Однако будучи подключённым к постоянной цепи, он всё же может его проводить в момент подсоединения, поскольку происходит зарядка или перезарядка.
Когда завершается переходный процесс, ток перестаёт проходить через пассивный электронный компонент из-за разделения его обкладок диэлектриком. Будучи подключённым к такой цепи он проводит его колебания вследствие циклической перезарядки. Здесь прибор входит в колебательный контур и вместе с катушкой выполняет функцию накопителя энергии.
Такой симбиоз способствует преобразованию электричества в магнитную энергию или, наоборот, с равной их собственной частотной скоростью, которая рассчитывается по формуле: omega = 1 / sqrt(C × L).
Действительность такова, что конденсатор не способен пропускать через себя переменный ток. Сначала он его аккумулирует на обкладках. Возникает ситуация, в которой на одной из них имеет место переизбыток электронов, а на другой их, напротив, мало. В результате конденсатор отдаёт эти заряды, из-за чего электроны, находящиеся во внешней цепи, перемещаются в одну и в другую сторону от одной обкладки к другой.
К сведению! Результат выражается в том, что электроны перемещаются внутри внешней цепи, но не в самом пассивном компоненте. Энергия перераспределяется внутри поля между конденсаторными пластинками, что называют токами смещения, отличающимися от электротоков проводимости.
История накопителей заряда
Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.
Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.
Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.
Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:
Формулы вычисления тока в конденсаторе
Ёмкость конденсатора, включенного в цепь переменного тока, рассчитывается по формуле: C = q / U, где:
- С — ёмкость;
- q — заряд одной из пластин;
- U — напряжение внутри.
- плоский — C = E × E0 × S / d;
- цилиндрический — С=2 π × E × E0 × l / ln(R2 / R1);
- сферический — C = 4 π ×E × E0 × R1 × R2 / R2 — R.
Обратите внимание! Сопротивление в переменной цепи, которое может оказывать резистор, включённый в электрическую цепь, вычислить нельзя, так как она считается бесконечно большим. Однако в данном случае, это можно сделать по формуле: Хс = 1 / 2πvC = 1 / wC.
Вам это будет интересно Пускатель звезда треугольник
Напряжение конденсатора в цепи переменного тока вычисляется по следующей формуле: Wp = qd E / 2.
Чтобы рассчитать напряжение на конденсаторе в цепи переменного тока, необходимо воспользоваться актуальными формулами.
Векторная диаграмма и полное сопротивление цели
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
u = u1R + uL + uC + u2R,
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
U = U2R + UL + UC +U2R
Для построения векторной диаграммы находим:
U1R = IR1; U2R = IR2; UL = IXL; UC = IXC.
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:
1. ХL>ХC . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
Векторная сумма напряжений U1 + U2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: Ua = U1R + U2R.
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: Uр = UL — UC .
При одинаковом токе во всех элементах цепи UL>UC . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
где R = R1 + R2 и X = XL — XC общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
U = IZ; I = U/Z; Z = U/I.
Из треугольников напряжения и сопротивлений определяют следующие величины:
Угол сдвига по фазе между напряжением и током в цепи положительный (φ>0) (фазовые токи отсчитываются от вектора тока).
2. ХLCВекторная диаграмма изображена на рис. 14.3, где ULC , поэтому общее напряжение отстает от тока на угол φ
Реактивное сопротивление цепи носит емкостный характер.
Расчетные формулы для первого случая остаются без изменения и для второго случая.
3. XL = ХC . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: UL = UC (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.
Общее напряжение совпадает по фазе с током и равно по величине активной
составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
U = IR, или I = U/R.
В случае XL = ХC в цепи имеет место явление резонанса напряжений.
Где и зачем применяются конденсаторы
Где и почему используются эти приборы, которые могут работать в радиотехнических, электронных и электротехнических устройствах? Накопители используются в электротехнике при включении асинхронных моторов для сдвига фаз, без чего двигатель в составе однофазной цепи не будет функционировать. Если ёмкость составляет несколько фарад, то их применяют в электромобилях для питания мотора.
Правильное использование этих приборов позволит получить лучший результат. Понимание основных принципов физики упрощает эксплуатацию оборудования. Неправильное применение чревато негативными последствиями, вызванными несоблюдением техники безопасности.
Сферы применения
Можно смело сказать, что конденсаторы используют практически во всех электронных и радиотехнических схемах. Чтобы иметь представление о том, где и зачем нужен конденсатор, следует вспомнить его способность сохранять заряд и разряжаться в нужное время, а также пропускать переменный ток и не пропускать постоянный. А это значит, что такие устройства используются во многих технических сферах, например:
- телефонии;
- в производстве счётных и запоминающих устройств;
- автоматике;
- при создании измерительных приборов и многих других.
Нужно сказать, что накопители применяют и в сферах, не связанных с электрикой, например, в производстве металла и добыче угля, где используют конденсаторные электровозы.
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля
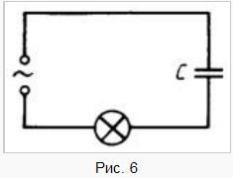
Рассмотрим
процессы, протекающие в электрической
цепи переменного тока с конденсатором.
Если подключить конденсатор к источнику
постоянного тока, то в цепи возникнет
кратковременный импульс тока, который
зарядит конденсатор до напряжения
источника, а затем ток прекратится. Если
заряженный конденсатор отключить от
источника постоянного тока и соединить
его обкладки с выводами лампы накаливания,
то конденсатор будет разряжаться, при
этом наблюдается кратковременная
вспышка лампы.
При
включении конденсатора в цепь переменного
тока процесс его зарядки длится четверть
периода. После достижения амплитудного
значения напряжение между обкладками
конденсатора уменьшается и конденсатор
в течение четверти периода разряжается.
В следующую четверть периода конденсатор
вновь заряжается, но полярность напряжения
на его обкладках изменяется на
противоположную и т.д. Процессы зарядки
и разрядки конденсатора чередуются с
периодом, равным периоду колебаний
приложенного переменного напряжения.
Как
и в цепи постоянного тока, через
диэлектрик, разделяющий обкладки
конденсатора, электрические заряды не
проходят. Но в результате периодически
повторяющихся процессов зарядки и
разрядки конденсатора по проводам,
соединенным с его выводами, течет
переменный ток. Лампа накаливания,
включенная последовательно с конденсатором
в цепь переменного тока (рис. 6), кажется
горящей непрерывно, так как человеческий
глаз при высокой частоте колебаний силы
тока не замечает периодического
ослабления свечения нити лампы.
Установим
связь между амплитудой колебаний
напряжения на обкладках конденсатора
и амплитудой колебаний силы тока. При
изменениях напряжения на обкладках
конденсатора по гармоническому закону
заряд
на его обкладках изменяется по закону:
Электрический
ток в цепи возникает в результате
изменения заряда конденсатора: i = q’.
Поэтому колебания силы тока в цепи
происходят по закону:
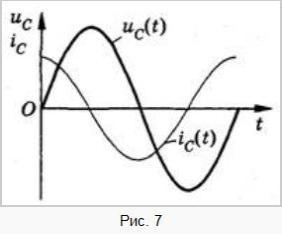
Следовательно,
колебания напряжения на обкладках
конденсатора в цепи переменного тока
отстают по фазе
от колебаний силы тока на р/2 или колебания
силы тока опережают по фазе колебания
напряжения на р/2 (рис. 7). Это означает,
что в момент, когда конденсатор начинает
заряжаться, сила тока максимальна, а
напряжение равно нулю. После того как
напряжение достигает максимума, сила
тока становится равной нулю и т.д.
Произведение
Um⋅щ⋅C
является амплитудой колебаний силы
тока:
Отношение
амплитуды колебаний напряжения на
конденсаторе к амплитуде колебаний
силы тока называют емкостным сопротивлением
конденсатора (обозначается ХC):
Связь
между амплитудным значением силы тока
и амплитудным значением напряжения по
форме совпадает с выражением закона
Ома для участка цепи постоянного тока,
в котором вместо электрического
сопротивления фигурирует емкостное
сопротивление конденсатора:
Емкостное
сопротивление конденсатора, как и
индуктивное сопротивление катушки, не
является постоянной величиной. Оно
обратно пропорционально частоте
переменного тока. Поэтому амплитуда
колебаний силы тока в цепи конденсатора
при постоянной амплитуде колебаний
напряжения на конденсаторе возрастает
прямо пропорционально частоте.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ТОЭ › Расчет цепей синусоидального тока
При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости, через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток).Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.
Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.
Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(P = 0).
Что такое конденсатор
Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.
Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).
Схема замещения конденсатора с последовательным соединением элементов
Реальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Хс сопротивлениями. На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13. 18,6). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным. Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью С Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а. Если вам интересно прочитайте статью о настоящих конденсаторах которые применяются в промышленности.
Характеристики конденсаторов
Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.
Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.
Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.
В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.
Вам это будет интересно Особенности расчета мощности по току и напряжению
Треугольник проводимостей для конденсатора
Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная G = IG/U и емкостная Вс = Iс/U проводимости, а гипотенузой — полная проводимость цепи Y = I/U. Из треугольника проводимостей
Связь между действующими величинами напряжения и тока выражается формулами
I = UY
U = I/Y (13.35)
Из треугольников токов и проводимостей определяют величины
cosφ = IG/I = G/Y; sinφ = Ic/I = Bc/Y; tgφ = IC/IG = Bc/G. (13.36)
В чем измеряется напряжение конденсаторов
Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.
Мощность цепи с конденсатором
Выражение мгновенной мощности реального конденсатора
p = ui = Umsinωt * Imsin(ωt+φ)
совпадает с выражением мгновенной мощности катушки. Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17. Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19) — (13.22)]. Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U. В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности; активная
P = UIG = UIcosφ
реактивная
Q = UIC = UIsinφ
полная
Что влияет на напряжение конденсаторов
Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд. Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.
Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.
Схема замещения конденсатора с параллельным соединением элементов
Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной Bс проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе G = Р/Uc2, а емкость — конструкцией конденсатора. Предположим, что проводимости G и Вс для такой цепи известны, а напряжение имеет уравнение
u = Umsinωt.
Требуется определить токи в цепи и мощность. Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них так же синусоидальны. При параллельном соединении ветвей G и Вс , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:
i = iG + ic, (13.30)
Учитывая, что ток iG совпадает по фазе с напряжением, а ток ic опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:
Как вычислить напряжение и вольтаж
Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.
Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.
Устройство конденсатора
Конденсатор представляет собой две проводящие поверхности, разделённые слоем диэлектрика. Как правило, эти поверхности делаются из тонкой медной или алюминиевой фольги, иногда свёрнутой в рулон. В качестве диэлектрика применяется бумага, керамика, некоторые виды пластмасс. От каждой из проводящих поверхностей (они называются обкладками) выводится электрический контакт — клемма. Вся конструкция помещается в корпус, обеспечивающий механическую прочность.
Формулы измерения напряжения конденсаторов
Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.
Вам это будет интересно Обозначение разного электрооборудованья на схемах
В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.
Векторная диаграмма токов в цепи с конденсатором
Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению
I = IG + IC
Действующие величины составляющих тока:
IG = GU (13.31)
IC = BCU (13.32)
Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φa =0). Вектор IG совпадает по направлению с вектором U, а вектор IC направлен перпендикулярно вектору U с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90º. Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC :
i = Imsin(ωt + φ)
Переменный ток
Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока
. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.
Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем). Заряженный конденсатор для постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен резистору с некоторым вполне определенным сопротивлением (если пока забить забыть про всякие там сдвиги фазы, об этом ниже). Нам надо каким-нибудь образом получить связь между током и напряжением на конденсаторе.
Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор. Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.
Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение
Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt. Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.
Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением
Давайте-ка выразим из этой формулы заряд конденсатора:
А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:
Емкость конденсатора у нас является величиной постоянной
. Она определяется
исключительно самим конденсатором
, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость
С
конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением
U
нельзя так поступить!
Напряжение на конденсаторе будет изменяться со временем. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него. Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.
А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:
По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.
Рисунок 1 – Поясняющая картинка
На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.
Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения.
Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения
U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.
Пусть напряжение на конденсаторе емкостью C
изменяется по закону синуса вот таким вот образом
Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше. Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную
Или можно записать вот так
Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то . Не понятно, откуда взялось это выражение? Погуглите формулы приведения
. Штука полезная, знать не помешает. А еще лучше, если вы хорошо знакомы с
тригонометрическим кругом
, на нем все это видно очень наглядно.
Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок. Итак, сейчас мы получили немаловажный вывод – если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов.
Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости
C
конденсатора, амплитуды приложенного к нему напряжения
U
m и частоты
ω
. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).
Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе
На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе. По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).
Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t)
через конденсатор емкостью
C
. И закон этот пусть тоже будет синусоидальным
Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:
По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом
Здесь мы снова воспользовались интересными сведениями из тригонометрии, что . И снова формулы приведения
придут вам на помощь, если не понятно, почему получилось именно так.
Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов. Более того, они не просто так сдвинуты. Ток опережает
напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.
Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.
Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.
Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем.
Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.
Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.
Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото )
Рисунок 3 – Ищем ток через этот конденсатор
Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.
Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное
значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону
Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так
Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока
Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало. Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует . Однако на этом принципе возможно изготовление так называемых источников питания с гасящим конденсатором. Ну да это тема для отдельной статьи и здесь мы не будем ее затрагивать.
Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.
Рисунок 4 – График напряжения в розетке
Рисунок 5 – График тока через конденсатор
Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть. И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla
Нет конденсатора нужного номинала: что делать
Очень часто начинающие домашние мастера, обнаружив поломку прибора, стараются самостоятельно обнаружить причину. Увидев сгоревшую деталь, они стараются найти подобную, а если это не удаётся, несут прибор в ремонт. На самом деле, не обязательно, чтобы показатели совпадали. Можно использовать конденсаторы меньшего номинала, соединив их в цепь. Главное – сделать это правильно. При этом достигается сразу 3 цели – поломка устранена, приобретён опыт, сэкономлены средства семейного бюджета.
Попробуем разобраться, какие способы соединения существуют и на какие задачи рассчитаны последовательное и параллельное соединение конденсаторов. Часто без соединения конденсаторов в батарею не обойтись. Главное – сделать это правильно
Действие конденсатора
Казалось бы, с точки зрения электрического тока конденсатор представляет собой разрыв цепи. Однако это не совсем так. Если создать на одной из обкладок конденсатора избыток свободных носителей электрического заряда, то свободные носители такого же знака начнут уходить с другой обкладки, а носители противоположного знака — наоборот, собираться на ней. То есть и на другой обкладке носители придут в движение.
Получается, что конденсатор не является полным разрывом электрической цепи. Если изменения заряда на первой обкладке производить попеременно, то в одну, то в другую сторону (подав на обкладку переменный ток) — то на второй обкладке заряды также будут попеременно двигаться.
Конденсатор способен передавать переменный ток, а также любые изменения тока вообще. Он является разрывом цепи только для постоянного тока.
Как проверить качество соединения конденсаторов в цепи
Самый идеальный случай, когда у нас на руках имеется соответствующего типа вольтметр. Он стоит в пределах одной тысячи рублей.
Это не так много, учитывая, что вкупе мы получаем прибор для измерения сопротивлений, постоянного и переменного напряжения, токов.
Гнездо под измерение конденсатор (см. фото слева) представляет собой две узкие щели, куда должны вставляться ножки.
По нашим наблюдениям нет разницы, какой стороной вставлять электролитический конденсатор. Хотя лучше все же руководствоваться инструкцией по эксплуатации.
Ззатем как-то нужно промаркировать их, либо разложить по нарисованной на бумаге схеме, где уже проставлять все цифры (кстати, так обычно и делается во всей китайской технике).
Затем следует вычислить по формулам, какое именно значение должно получиться и проверить это тестером. Не получается? Значит, качество контактов плохое – меньше применяйте скруток.
СОЕДИНЕНИЯ КОНДЕНСАТОРОВ
Если необходимо увеличить общую емкость конденсаторов, то их соединяют между собой параллельно (рис. 9, а
). При этом способе соединения общая площадь пластин увеличивается по сравнению с площадью пластины каждого конденсатора. Общая емкость конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов и вычисляется по формуле Собщ=С1 + С2+С3+
(10)
Это можно подтвердить следующим образом.
Соединенные параллельно конденсаторы находятся под одним и тем же напряжением, равным U вольт, а общий заряд этих конденсаторов равен q кулонов. При этом каждый конденсатор соответственно получает заряд q 1 , q 2 , q 3, и т. д. Следовательно,
q общ = q 1 + q 2 + q 3 +
Из формулы (8) вытекает, что заряд
q общ = С общ U (11)
а заряды q 1 = С 1 U; q 2 = С 2 U; q 3 = С 3 U.
Подставив эти выражения в формулу (11), получим:
С общ U= С 1 U + С 2 U + С 3 U.
Разделив левую и правую части этого равенства на равную для всех конденсаторов величину U, после сокращения найдем:
С общ = С 1 + С 2 + С 3
Пример
. Три конденсатора емкостью С 1 =2 мкф ; C 2 =0,1 мкф и C 3 =0,5 мкф соединены параллельно.
Вычислить их общую емкость.
С общ = С 1 + С 2 + С 3 =2+00,1+0,5=2,6 мкф.
Общую емкость конденсаторов, имеющих одинаковую емкость и соединенных параллельно, можно вычислить по формуле
С общ = Сn, (12)
где С — емкость одного конденсатора,
n — число конденсаторов.
Пример.
Пять конденсаторов емкостью 2 мкф каждый соединены параллельно. Определить их общую емкость.
С общ = Сn =2·5=10 мкф.
Конденсаторы соединяют последовательно (рис. 9, б), когда рабочее напряжение установки превышает напряжение, на которое рассчитана изоляция одного конденсатора. В этом случае правую пластину первого конденсатора соединяют с левой пластиной второго, правую пластину второго — с левой пластиной третьего и т. д. Общая емкость конденсаторов при таком соединении уменьшается. Величина, обратная общей емкости конденсаторов, соединенных последовательно , равна сумме обратных величин емкостей отдельных конденсаторов:
Это можно подтвердить следующим образом. Общее напряжение на конденсаторах U общ а на каждом конденсаторе U 1 , U 2 , U 3 , тогда
U общ = U 1 +U 2 + U 3 .
Из Формулы (8) следует, что напряжение
U общ = (14)
а напряжение
Подставив эти выражения в формулу (14), получим:
Разделим левую и правую части этого равенства на величину q и после сокращения найдем:
Пример. Три конденсатора С1=2 мкф, С2=4 мкф и С3=8 мкф соединены последовательно. Определить их общую емкость.
Если последовательно соединены конденсаторы, имеющие одинаковую емкость, то их общую емкость можно вычислить по формуле
Пример.
Четыре конденсатора емкостью 1000 пф каждый соединены последовательно. Определить их общую емкость. Решение.
Если последовательно соединены два конденсатора различной емкости, то их общую емкость можно найти по формуле
Пример.
Два конденсатора С 1 =200 пф
и С 2 =300 пф соединены последовательно. Вычислить их общую емкость.
Как видно из приведенных примеров, общая емкость конденсаторов, соединенных последовательно, всегда меньше наименьшей емкости, входящей в соединение.
Конденсаторы выбирают по емкости и рабочему напряжению которое подается на его пластины при включении в схему. При напряжении, превышающем допустимое, происходит пробой диэлектрика в конденсаторе. Это напряжение называется пробивным. Пробой диэлектрика сопровождается электрическим разрядом — искрой с характерным треском. Конденсатор с пробитым диэлектриком не пригоден для применения.
Каждый диэлектрик обладает определенной электрической прочностью, т. е. способностью противостоять пробою. Электрическая прочность (табл. 2) измеряется обычно в (в/см
) и определяется по формуле
где U — напряжение, в
d — толщина диэлектрика, см.
Многие, собирая тот или иной прибор, часто задумываются о том, как соединить конденсаторы параллельным или последовательным соединением. Далеко не каждый номинал выпускается промышленностью, поэтому задача обеспечить конструкцию связкой ёмкостей встречается тут и там. При параллельном включении номиналы складываются, а при последовательном используется более сложная формула. А ещё конденсаторы бывают подстроечными, такие совершенно точно включаются в цепи, где требуется обеспечить нужные резонансные характеристики. В этом случае также требуется решить указанную выше задачу. Проблема ещё в том, что часто сборка какого-нибудь индукционного нагревателя идёт буквально на коленках, железа целая кипа, колодок под рукой нет, а паять лень – что делать?