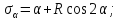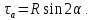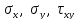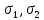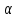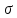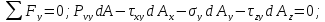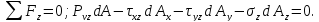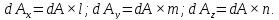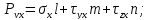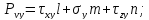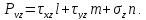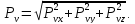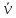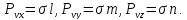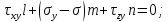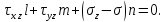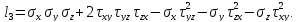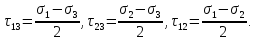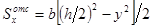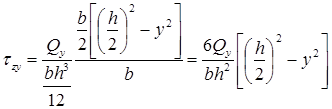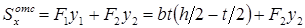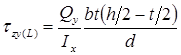Пример нахождения графическим способом по кругу Мора, величины и направления главных напряжений по известным нормальным и касательным напряжениям.
Задача
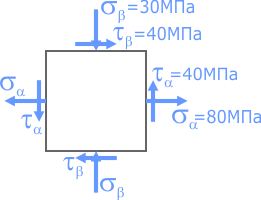
Определить величину, знак и направление главных напряжений с помощью круга Мора по заданным нормальным и касательным напряжениям на гранях элемента.
Другие примеры решений >
Помощь с решением задач >
Пример решения
Предыдущий пункт решения задачи — построение круга Мора
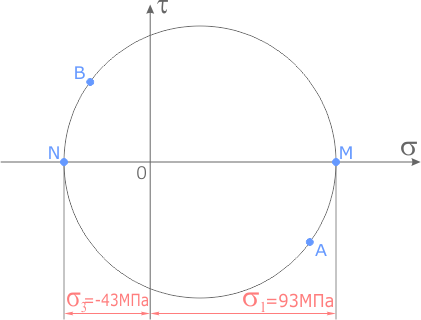
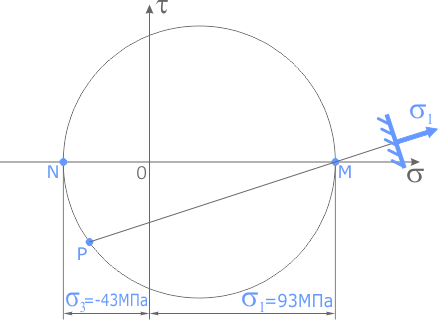
Как было показано ранее, координаты точек пересечения круга Мора с осью напряжений σ показывают величину главных напряжений.
В данном случае главные напряжения в точке элемента составляют
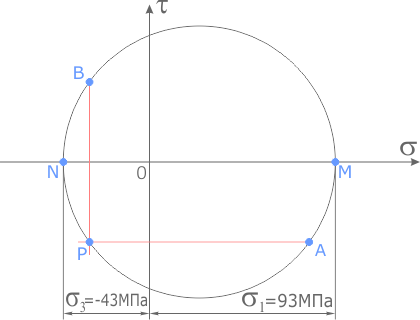
Для определения направления главных напряжений выполним следующие действия:
Из точки A проводим луч влево, а из точки B вниз до пересечения.
Точка их пересечения обозначается буквой P и является полюсом круга Мора. Очевидно, она будет располагаться на окружности.
Луч, проведенный из полюса через точку М, показывает направление главного напряжения σ1.
Так как точка M расположена в области положительных значений σ то по правилу знаков соответствующее главное напряжение будет растягивающим (стрелка напряжения направляется от площадки).
Аналогично, луч [PN) показывает направление главного напряжения на смежной площадке элемента.
Расположение точки N слева от пересечения осей σ—τ указывает на то, что это напряжение сжимающее (стрелка напряжения направлена в сторону площадки).
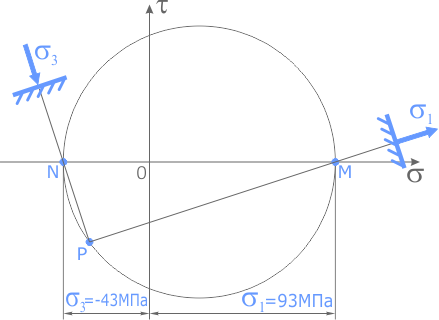
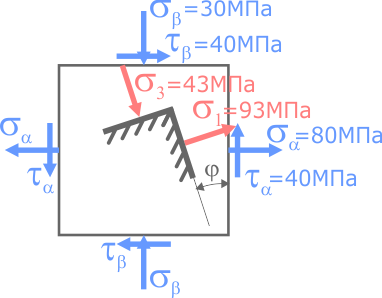
Покажем полученные напряжения на заданном элементе.
Для наглядности, главные площадки изображаются в пределах заданного элемента.
Здесь видно, что в сечении элемента расположенном под углом φ к начальному, касательные напряжения исчезают, а нормальные изменив величину, становятся главными.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Зависимость
напряжений от угла наклона площадки,
на которой они действуют, имеет простую
геометрическую интерпретацию в виде
диаграммы, которая называется кругом
напряжений Мора. Обозначим:
Тогда
напряжения на наклонных площадках можно
представить в виде:
Эти
уравнения представляют окружность в
параметрической форме. Они эквивалентны
уравнению:
Используя
круги Мора, можно решать два типа задач.
Первый
тип.
Пусть известны напряжения
на произволь-ных площадках. Требуется
найти главные напряжения
и положение главных площадок.
Решение.
По оси
(рис. 7.6) отложим отрезок

равный по величине

7.6. Схема круга Мора для нахождения
главных напряжений
и
положения главных площадок
Из
точки
в направлении оси
отложим отрезок
соответствующий

Аналогично построим точки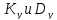
равные напряжениям
Соединив точки

получим точку С
пересечения отрезка
с осью

Вокруг точки С опишем окружность
диаметром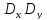
Это и будет окружность напряжений Мора.
Точки
А
и В
пересечения окружности с осью σ
соответствуют главным напряжениям
Для определения направления главных
площадок из точки
проведем прямую параллельно оси
до пересечения с окружностью в точке
М,
которая называется полюсом. Прямые,
проведенные из полюса в точки А
и В,
соответствуют направлению главных
напряжений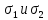
Второй
тип. Пусть
известны главные напряжения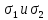
Требуется определить напряжения на
площадках, направленных под углом
к главным.
Решение.
Вдоль оси
(рис. 7.7, б) отложим отрезки ОА
и ОВ,
соответствующие главным напряжениям
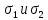
На отрезке АВ,
как на диаметре, построим окружность
напряжений Мора. Из центра окружности
(точка С)
отложим центральный угол 2α
с осью σ и проведем прямую до пересечения
с окружностью в точках Dα
и
Dβ.
Рис.
7.7. Схема круга Мора для нахождения
напряжений
на
второстепенных площадках
Координаты
этих точек соответствуют напряжениям
на площадках, повернутых на угол
и на площадке, на которой действует
главное напряжение

Положения этих площадок получим, проведя
из точки В
прямые до пересечения с окружностью в
точках

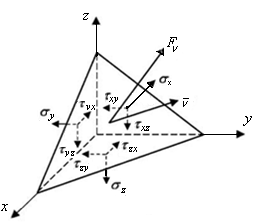
7.7. Объемное напряженное состояние
В
общем случае напряженного состояния
на гранях элементарного
параллелепипеда,
выделенного в окрестности точки
нагруженного тела, действует девять
компонентов тензора напряжений. В силу
закона парности касательных напряжений
независимыми являются только шесть из
них.
Вычислим
напряжения на произвольной площадке
ABC
с вектором нормали ν
в окрестности произвольной точки О
(см. рис. 7.7). Обозначим направляющие
косинусы вектора нормали ν
к площадке ABC
величинами:
Проекции
полного напряжения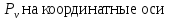
действующего на площадке АВС,
обозначим
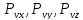
Для их определения составим уравнения
равновесия четырехгранника, выделенного
координатными плоскостями и плоскостью
АВС
в окрестности произвольной точки
нагруженного тела (рис. 7.8):
Площади
граней элементов связаны между собой
зависимостями:
Учитывая
это,
получим:
Нормальные
напряжения найдем, составив сумму
проекций на направление нормали:
Полное
напряжение на площадке:
Касательное
напряжение на площадке:

Определение
главных напряжений.
Пусть
площадка АВС
(рис. 7.8) – главная, а нормаль к ней
совпадает с главной осью. Касательные
напряжения на этой грани отсутствуют,
а нормальное напряжение совпадает с
полным. Проекции этого напряжения на
координатные оси равны:
Учитывая
выражение для

получим:
Эти
равенства можно рассматривать, как
однородную систему линейных алгебраических
уравнений относительно l,
m
и n.
Рис.
7.8. Схема площадки для определения
главных
напряжений
Так
как направляющие косинусы связаны
соотношениями
l
+ m
+ n
= 1, нулевое решение этой системы
невозможно. Нулевое решение системы
возможно только в том случае, когда
определитель, составленный из ее
коэффициентов при неизвестных, обращается
в нуль, т. е.

Раскрыв
этот определитель, получим кубическое
уравнение относительно главного
напряжения
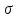
где
В
силу симметрии определителя относительно
главной диагонали, соответствующее ему
кубическое уравнение имеет три
действительных корня, три главных
напряжения:

Главные
напряжения в точке нагруженного тела
не зависят от выбора системы координат.
Поэтому
и
называют их соответственно первым,
вторым и третьим инвариантами тензора
напряжений. Их можно представить в виде:

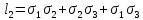
В
случае объемного напряженного состояния
напряжения также можно представить
графически. Если рассмотреть наклонные
площадки, параллельные одному из главных
напряжений, то для них справедливы
формулы для плоского напряженного
состояния. Из рис. 7.9 видно, что напряжение
σ3
не влияет на величину напряжений σα
и
τα,
действующих
на площадке, параллельной σ3.
Тогда напряжения на таких площадках
можно представить графически, построив
круг Мора на главных напряжениях σ1
и σ2.
Аналогично можно представить графически
напряжения на наклонных площадках,
параллельных σ1
и σ2,
как показано на рис. 7.10. Однако точки,
расположенные на этих трех кругах, не
исчерпывают всех наклонных площадок в
точке нагруженного тела.
Рис.
7.9. Схема наклонной площадки при объемном
напряженном
состоянии
Можно
показать, что площадкам общего положения
соответствуют точки на плоскости,
лежащие в заштрихованной области между
тремя кругами Мора. Точки, являющиеся
вершинами этих кругов, соответствуют
площадкам, наклоненным под углом 45о
к соответствующим главным площадкам.
Рис.
7.10. Круги Мора для определения
касательных
напряжений
Касательные
напряжения на этих площадках равны
радиусам кругов Мора и определяются
формулами:
Максимальное
касательное напряжение
iSopromat.ru
Пример нахождения графическим способом по кругу Мора, величины и направления главных напряжений по известным нормальным и касательным напряжениям.
Определить величину, знак и направление главных напряжений с помощью круга Мора по заданным нормальным и касательным напряжениям на гранях элемента.
Пример решения
Предыдущий пункт решения задачи — построение круга Мора
Как было показано ранее, координаты точек пересечения круга Мора с осью напряжений σ показывают величину главных напряжений.
В данном случае главные напряжения в точке элемента составляют
Для определения направления главных напряжений выполним следующие действия:
Из точки A проводим луч влево, а из точки B вниз до пересечения.
Точка их пересечения обозначается буквой P и является полюсом круга Мора. Очевидно, она будет располагаться на окружности.
Луч, проведенный из полюса через точку М, показывает направление главного напряжения σ 1.
Так как точка M расположена в области положительных значений σ то по правилу знаков соответствующее главное напряжение будет растягивающим (стрелка напряжения направляется от площадки).
Аналогично, луч [PN) показывает направление главного напряжения на смежной площадке элемента.
Расположение точки N слева от пересечения осей σ — τ указывает на то, что это напряжение сжимающее (стрелка напряжения направлена в сторону площадки).
Покажем полученные напряжения на заданном элементе.
Для наглядности, главные площадки изображаются в пределах заданного элемента.
Здесь видно, что в сечении элемента расположенном под углом φ к начальному, касательные напряжения исчезают, а нормальные изменив величину, становятся главными.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Графическое определение напряжений (круг Мора)





Графическое определение напряжений (круг Мора)
Графическое определение давления(круг Мора). Расчет АА и та по формулам (7.5) и (7.6) может быть заменен графической конфигурацией (рис.). 79). Положительная ось o направлена вправо. Поместите его на оси o сегментов OA и OB, и нарисуйте числовое
значение напряжения на определенном масштабе Компрессия, Напряжение тока внутри). Как использовать 79 предполагается, что оба эти напряжения являются растягивающими и осаждаются на оси а в положительном направлении. Если бы было одно или
оба этих напряжения, мы бы направили их в противоположном направлении Людмила Фирмаль
. Построить отрезок AB как диаметр, центр C и окружность, он называет напряжение вокруг, » затем найти нормальное и касательное напряжение TA OA на полу, точка D лучшего Mei напряжения круга соответствует выбранному участку и его координаты OK и DK соответственно aa и TA. Это легко доказать.
Из рисунка находим радиус окружности напряжений: CD=AC=BC=L2B=;§ 37] графическое определение напряжений 129 Из правого треугольника получаем: DK = CD sin2A=sin2A Рядом: О’а ’=о’В4-для sun4-СК=А2 4-4-Щ п cos2A==3-2 4
- OA измеряются в сегментах вдоль оси A. положительные отложены в положительном направлении оси O. размер сегмента измеряется параллельно оси, поэтому положительный ТВ вверх, = Р sin2A Р, Это для тебя! Выбрано самое высокое из основных напряжений. После определения напряжений ОА и та путем построения окружности нарисуйте их на схеме выбранных элементов с учетом признаков
этих напряжений(рис. 79). Мы всегда соглашались считать угол a, определяющий положение внешней нормали к рассматриваемому участку, от линии действия главного напряжения (алгебраически) до максимума его главной оси напряжения Людмила Фирмаль
напряжения равно радиусу сегмента CD0, т. е. окружности напряжения Макс 2′ Соответствующий угол 2a равен 90°, а угол a=45°. В круге напряжений значение tah TA представлено абсциссой ординаты CDQ), обеспечиваемой ОС=ST1y -. Из рисунка тоже. 79 максимальное нормальное напряжение представлено отрезком O A и равно минимальному отрезку OB и равно A2. Величина нормального напряжения на любом из рассматриваемых участков с углом а находится между значениями главных напряжений、 5II. М. Belyaev130 сложном напряженном состоянии 1gl. ВХ Зная основное напряжение для плоского напряженного
состояния, можно синтетически исследовать напряженное состояние материала в точке, используя круг напряжений. П р и М Е Р20. Найти на графике напряжение и TA участка под углом a=-30°, основное напряжение A3= — 700 кг / СМ1 и gj= — f-300 кг / см. Структура является Fig. It отдается в руки. 80: ОА=4 ″ 50км! см ОП= — 430kg; см. Вы можете использовать круги напряжений, чтобы найти известные главные напряжения и напряжения O2, перпендикулярные друг другу нормаль к участку а-а и Б-Б, который является Лар (рис. 81) составляют углы a и b с направлением максимального главного напряжения в окружности напряжений(рис. 81) в точке с построить угол 2А. Точке B соответствует участок а-а, Дак и сегментыи » Ока «
представляют напряжений та и ОА этого сайта. Для того чтобы найти напряжение на участке b-b, необходимо добавить угол 2





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
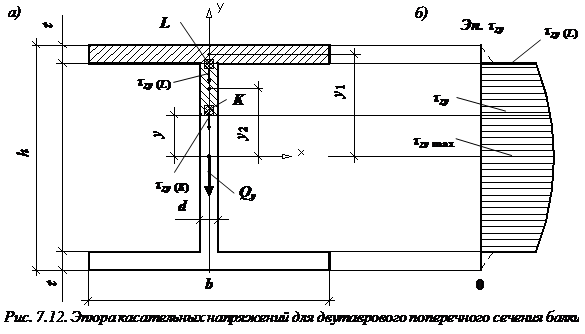
Эпюры касательных напряжений для прямоугольного, двутаврового, круглого сечений
Эпюры касательных напряжений прямоугольного сечения
При выводе формулы Журавского предполагалось: балка имеет прямоугольное поперечное сечение (рис. 7.11), поэтому
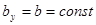
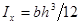
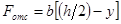
где y – расстояние от точки, в которой определяется касательное напряжение, до нейтральной оси x.
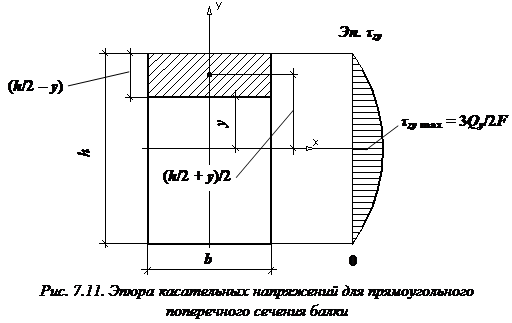
Касательные напряжения изменяются по высоте поперечного сечения по закону квадратичной параболы (см. рис. 7.11).
При 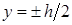
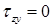
Для точек, расположенных на нейтральной оси (при 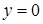
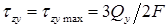
Эпюры касательных напряжений двутаврового сечения
Характерная особенность двутаврового сечения: резкое изменение ширины поперечного сечения (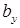
Определим касательное напряжение в некоторой точке K (рис. 7.12), проведя через нее сечение, ширина которого равна толщине стенки: 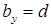
Рассмотрим верхнюю отсеченную часть поперечного сечения (заштрихована на рис. 7.12), статический момент инерции которой относительно нейтральной оси x равен сумме статических моментов инерции полки и заштрихованной части стенки:
Эпюра касательных напряжений для двутаврового сечения представлена на рис. 7.12, б.
Касательные напряжения 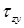
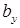
Формула касательного напряжения в точке L ( где полка соединяется со стенкой):
Наибольшие касательные напряжения возникают в точках, лежащих на нейтральной оси x.
Эпюры касательных напряжений круглого сечения
Для построения эпюры касательных напряжений круглого сечения выясним направление касательных напряжений при изгибе , возникающих в некоторой точке контура поперечного сечения стержня.
Предположим: в некоторой точке контура К касательное напряжение при изгибе 
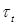
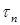
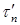
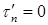
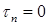
Таким образом, в точке контура поперечного сечения, поверхность которого не нагружена продольными внешними нагрузками, касательное напряжение при изгибе направлено по касательной к контуру.
Покажем, что в вершине угла поперечного сечения стержня касательное напряжение равно нулю (рис. 7.13, б).
Предположим, что в вершине угла (в точке M) возникает касательное напряжение 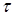
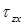
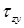
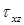
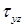
Наибольшие касательные напряжения, возникающие в точках, расположенных на нейтральной оси x, вычисляются по формуле:
Источник
3.5. ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ НА НАКЛОННЫХ ПЛОЩАДКАХ. КРУГ МОРА Известны значения главных напряжений σ1 и σ2, требуется найти напряжения на наклонных площадках. В системе координат σ – τ построен круг диаметром АВ, равным разности главных напряжений АВ = 0B – 0A = σ1 – σ2 (рис. 3.8). Из левой точки (А) пересечения круга с осью абсцисс проведен луч под углом α. Абсциссой точки D пересечения луча с кругом определяется нормальное напряжение σα на наклонной площадке, ординатой точки D – касательное τα. Напряженное состояние перпендикулярной площадки определяется координатами точки F(σβ, –τα). Радиус круга равен полуразности главных напряжений Абсцисса центра круга – среднее арифметическое главных напряжений Нормальное напряжение σα на наклонной площадке равно сумме отрезков Рис. 3.8. Круг Мора для определения напряжений на наклонных площадках Касательное напряжение на наклонной площадке τα = DE = CD•sin 2α Приведенные формулы по виду и нумерации совпадают формулами в §3.3. На практике нахождение напряжений на наклонных площадках иногда называют прямой задачей. Пример 3.1 Известны два главных напряжения (МПа), приложенных к элементарному параллелепипеду. Требуется найти нормальные и касательные напряжения, действующие на площадке, наклоненной под заданным углом α = –30°. Решение аналитическое Руководствуясь соотношением σ1 ≥ σ2 ≥ σ3, присваиваем индексы главным напряжениям: σ1 = 200 МПа, σ2 = 0, σ3 = –400 МПа. Решение графическое В координатных осях σ – τ откладываем напряженное состояние площадок В и С, выраженное парой координат (σ, τ): В(–400; 0); С(200; 0). Эти точки принадлежат диаметру круга. Из левой точки пересечения круга с осью абсцисс проводим луч под углом α = –30°. Координаты точки пересечения луча с кругом – искомые напряжения σα и τα. Вывод. Аналитическим и графическим способами найдены нормальные и касательные напряжения, действующие на наклонной площадке. Результаты решений совпали.
Нахождение главных напряжений при помощи круга.
- Найдите главное напряжение с помощью кругов. Иногда приходится решать задачу, находя основное напряжение обратным тому, которое описано в предыдущем пункте, а именно напряжение aa, TA. Самый
простой способ сделать это-использовать стресс-кольцо. Пусть (рис. 84) платформа на мы ния Фигура. 84.
Опишите разрез и ОВ — ^ Мы знаем нормали и касательные напряжения-перпендикулярные
Людмила Фирмаль
плоскости чертежа и составляющие прямой угол между ними. Обычное напряжение обозна -, Чим АА и касательная та и Т; следовательно, та= — т. условимся поставить значки а и^так(алгебраически). Предположим, что точно a≠>0 и TA>0.
Применим его к системе координат напряжений__ AA-al-V положительный угол a (угол поворота направления b) засчитывается по часовой стрелке, поэтому ставится знак минус. (Инжир. Можно определить уравнение для определения главного напряжения в
- плоском напряженном состоянии, показанное на рисунке 84. Из рисунков есть ОА=ОС и ОВ=ОС-СВ. tg2A (7.Х ) В дальнейшем: «И АА— 7. Около Значение и направление) —— Т-3И. OS=p; ska=C K=^ — радиус окружности напряжений SA-CD равен SV = CDZ: C. 4-SV = CD,=V C K i N-K, Di=]/(°I-Dr>■4 -= =4Ф у—г к — Следовательно, (51=O A ^ = ово> (7.12) 134 сложных напряженных состояния[Глава VII На практике часто
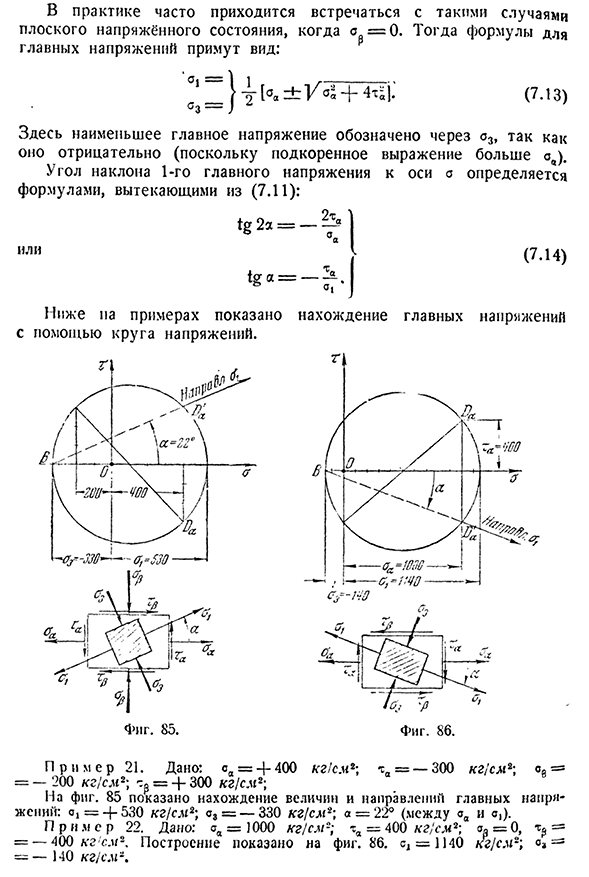
приходится встречать такой случай, как плоское напряженное состояние, когда^=0. После этого формула для основного напряжения будет иметь вид: Здесь самый низкий главный стресс, потому что он отрицательный (потому что подкорковое выражение больше, чем OA), обозначается O3. Угол наклона 1-го основного напряжения к оси o определяется уравнением, полученным из (7.11):
Или (7.14)) Следующий пример показан с использованием круга напряжения.
Людмила Фирмаль
Найти главные напряжения П р и М Е Р21. Дано: ОА=+400/гг/С. Да2; * ЦС= — 300кг / см2;O9== — 200кг / см2;+300кг/см2; на фиг. 85 указывает на нахождение величины и направления главного напряжения: 0! =4-530кг / см2; A3= — 330кг / см2;a=22 ° (между CA и ad P R и m E R 22. Дано: АА=1000кг / см2;та=400кг / см2;^=0,= — 400кг ’ см2, как показано на рисунке. 86. ^=1140кг / см2;= — 140 кг] см2.
Смотрите также:
- Решение задач по сопротивлению материалов