Как найти напряжение идеального вольтметра

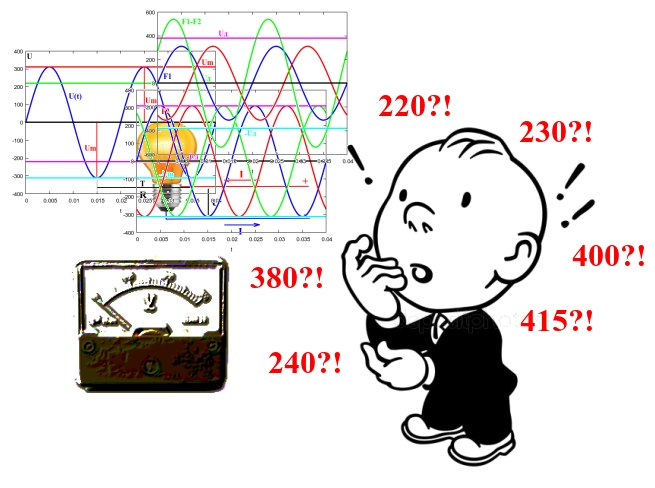
Что показывает вольтметр, или математика розетки

О чем эта статья

Сегодня я ненадолго отступлю от своей обычной темы о визуальном программировании контроллеров и обращусь к теме измерений напряжения прямо в ней, в розетке!

Родилась эта статья из дискуссий за чаем, когда разразился спор среди «всезнающих и всеведающих» программистов о том, чего многие из них не понимают, а именно: как измеряется напряжение в розетке, что показывает вольтметр переменного напряжения, чем отличается пиковое и действующие значения напряжений.

Скорее всего, это статья будет интересна тем, кто начинает творить свои устройства. Но, возможно, поможет и кому-то опытному освежить память.

В статье рассказано о том, какие напряжения есть в сети переменного тока, как их измеряют и о том, что следует помнить при проектировании электронных схем.
Всему дано краткое и упрощённое математическое обоснование, чтобы было ясно не только «как», но и «почему».

Кому не интересно читать про интегралы, ГОСТы и фазы — могут сразу переходить к заключению.

Вступление

Когда люди начинают говорить о напряжении в розетке, очень часто стереотип «в розетке 220В» скрывает от их взора реальное положение дел.

Начнем с того, что согласно ГОСТ 29322-2014, сетевое напряжение должно составлять 230В±10% при частоте 50±0,2Гц (межфазное напряжение 400В, напряжение фаза-нейтраль 230В). Но в том же ГОСТ имеется примечание: «Однако системы 220/380 В и 240/415 В до сих пор продолжают применять».

Согласитесь, что это уже совсем не то однозначное «в розетке 220В», к которому мы привыкли. А когда речь начинает идти о «фазном», «линейном», «действующем» и «пиковом» напряжениях — вообще каша получается знатная. Так сколько же вольт в розетке?

Чтобы ответить на этот вопрос начнем с того, как измеряется напряжение в сети переменного тока.

Как измерять переменное напряжение?

Прежде, чем углубиться в дебри цепей переменного тока и напряжения, вспомним школьную физику цепей тока постоянного.

Цепи постоянного тока — вещь простая. Если мы возьмем некоторую активную нагрузку (пусть это будет обычная лампа накаливания, как на рисунке) и воткнем ее в цепь постоянного тока, то все, что происходит в нашей цепи будет характеризоваться всего двумя величинами: напряжением на нагрузке U и током, протекающим через нагрузку I. Мощность, которая потребляется нагрузкой однозначно вычисляется по формуле, известной со школы: .

Или, если учесть, что по закону Ома , то мощность P, потребляемую нагрузкой-лампочкой, можно вычислить по формуле .

С переменным напряжением все куда сложнее: в каждый момент времени — оно может иметь разное мгновенное значение. Следовательно, в разные моменты времени, на нагрузке, подключенной к источнику переменного напряжения (например, на лампе накаливания, воткнутой в розетку) будет выделяться разная мощность. Это очень неудобно с точки зрения описания электрической цепи.

Но нам повезло: форма напряжения в розетке синусоидальная. А синусоида, как известно, полностью описывается тремя параметрами: амплитудой, периодом и фазой. В однофазных сетях (а обычная розетка с двумя дырочками именно и есть однофазная сеть) про фазу можно забыть. На рисунке подробно показаны два периода сетевого однофазного напряжения. Того самого, что в розетке.

Рассмотрим, что означают все эти буковки на рисунке.

Период T — это время между двумя соседними минимумами или соседними максимумами синусоиды. Для осветительной сети РФ этот период составляет 20 миллисекунд, что соответствует частоте 50Гц. Частота колебаний напряжения электрической сети выдерживается очень точно, до долей процента.

Очевидно, что в любых двух точках синусоиды, отстоящих друг от друга на целое число периодов, напряжения всегда равны между собой.

Амплитуда Um — это максимальное напряжение, пик синусоиды. Про действующее напряжение Uд поговорим чуть ниже.

Напряжение в розетке (или однофазной сети) описывается формулой

где t — текущий момент времени, Um — амплитуда (или пиковое значение) напряжения, T — период сетевого напряжения.

Если с однофазным переменным напряжением более или менее все ясно, то попробуем посчитать мощность, которая выделяется на нашей любимой лампе накаливания, при втыкании ее прямо в розетку.

Так как лампа накаливания является активной нагрузкой (а это значит, что ее сопротивление не зависит от частоты напряжения и тока), то мгновенная мощность, выделяемая на лампе накаливания, воткнутой в розетку, будет вычисляться по формуле

где t — текущий момент времени, а R — сопротивление лампы накаливания при нагретой спирали. Зная амплитуду переменного напряжения Um, можно записать:

Понятно, что мгновенная мощность — неудобный параметр, да и на практике не особо нужный. Поэтому практически обычно применяется мощность, усредненная за период.
Именно усредненная мощность указана на лампочках, нагревателях и прочих бытовых утюгах.

Рассчитывается усредненная мощность в общем случае по формуле:

А для нашей синусоиды — по гораздо более простой формуле:

Можете сами подставить вместо функцию и взять интеграл, если не верите.

Не думайте, что про мощность я вспомнил просто так, из вредности. Сейчас поймете, зачем она нам была нужна. Переходим к следующему вопросу.

Что же показывает вольтметр?

Для цепей постоянного тока, тут все однозначно — вольтметр показывает единственное напряжение между двумя контактами.

С цепями переменного тока все опять сложнее. Некоторые (и этих некоторых не так мало, как я убедился) считают, что вольтметр показывает пиковое значение напряжения Um, но это не так!

На самом деле, вольтметры обычно показывают действующее или эффективное, оно же среднеквадратичное, напряжение в сети Uд.

Разумеется, речь идет о вольтметрах переменного напряжения! Поэтому, если будете измерять вольтметром напряжение сети, обязательно убедитесь, что он находится в режиме измерения переменного напряжения.

Оговорюсь, что «пиковые вольтметры», показывающие амплитудные значения напряжения, тоже существуют, но на практике при измерении напряжения питающей сети в быту обычно не применяются.

Разберемся, почему такие сложности. Почему бы не измерять просто амплитуду? Зачем выдумали какое-то «действующее значение» напряжения?

А все дело в потребляемой мощности. Я ведь не просто так писал о ней. Дело в том, что действующее (эффективное) значение переменного напряжения равно величине такого постоянного напряжения, которое за время, равное одному периоду этого переменного напряжения, произведет такую же работу, что и рассматриваемое переменное напряжение.

Или, по-простому, лампочка накаливания будет светить одинаково ярко, воткнем ли мы ее в сеть постоянного напряжения 220В или в цепь переменного тока с действующим значением напряжения 220В.

Для тех, кто уже знаком с интегралами или еще не забыл математику, приведу общую формулу расчета действующего напряжения произвольной формы:

Из этой формулы также становится ясно, почему действующее (эффективное) значение переменного напряжения также называют «среднеквадратичным».

Заметим, что подкоренное выражение и есть та самая «усредненная за период мощность», стоит только поделить это выражение на сопротивление нагрузки R.

Применительно к синусоидальной форме напряжения, страшный интеграл после несложных преобразований превратится в простую формулу:

где Uд — действующее или среднеквадратичное значение напряжение (то самое, которое обычно показывает вольтметр), а Um — амплитудное значение.

Действующее напряжение хорошо тем, что для активной нагрузки, расчет усредненной мощности полностью совпадает с расчетом мощности на постоянном токе:

Это и не удивительно, если вспомнить определение действующего значения напряжения, которое было дано чуть выше.

Ну и, наконец, посчитаем, чему же равна амплитуда напряжения в розетке «на 220В«:

В худшем случае, если у вас сеть на 240В, да еще и с допуском +10%, амплитуда будет аж !

Поэтому, если хотите, чтобы ваши устройства, питающиеся от сети, работали стабильно и не сгорали, выбирайте элементы, которые выдерживают пиковые напряжения не менее 400В. Разумеется, речь идет об элементах, на которые непосредственно подаётся сетевое напряжение.

Отмечу, что для не-синусоидальной формы сигнала действующее значение напряжения рассчитывается по иным формулам. Кому интересно — могут сами взять интегралы или обратиться к справочникам. Нас же интересует питающая сеть, а там всегда должна быть синусоида.

Фазы, фазы, фазы…

Помимо обычной однофазной осветительной сети

220В все слышали и о трехфазной сети

380В. Что такое 380В? А это межфазное эффективное напряжение.

Помните, я сказал, что в однофазной сети про фазу синусоиды можно забыть? Так вот, в трехфазной сети этого делать нельзя!

Если говорить по простому, то фаза — это сдвиг во времени одной синусоиды относительно другой. В однофазной сети мы всегда могли принять за начало отсчета любой момент времени — на расчеты это не влияло. В трехфазной сети необходимо учитывать насколько одна синусоида отстоит от другой. В трехфазных сетях переменного тока каждая из фаз отстоит от другой на треть периода или на 120 градусов. Напомню, что период измеряется также в градусах и полный период равен 360 градусов.

Если мы возьмем осциллограф с тремя лучами и прицепимся к трем фазам и одному нулю, то увидим такую картину.

«Синяя» фаза — начинается от нуля отсчета. «Красная» фаза — на треть периода (120 градусов) позже. И, наконец «зеленая» фаза начинается на две трети периода (240 градусов) позже «синей». Все фазы абсолютно симметричны друг относительно друга.

Какую именно фазу брать за точку отсчета — не важно. Картина будет одинаковой.

Математически можно записать уравнения всех трех фаз:

«Синяя» фаза:

«Красная» фаза:

«Зеленая» фаза:

Если измерить напряжение между любой из фаз и нулем в трехфазной сети — то получим обычные 220В (или 230В или 240В — как повезет, см. ГОСТ).

А если измерить напряжение между двумя фазами — то получим 380В (или 400В или 415В — не забываем об этом).

То есть трехфазная сеть — многолика. Ее можно использовать как три однофазные сети с напряжением 220В или как одну трехфазную сеть с напряжением 380В.

Откуда взялось 380В? А вот откуда.

Если мы подставим в формулу расчета действующего напряжения наши данные о двух любых фазах, то получим:

Uдф — действующее межфазное, оно же линейное напряжение.

Учитывая, что амплитуда каждой фазы получим, чтодля межфазного напряжения. На рисунке наглядно показано, как образуется межфазное напряжение, которое обозначено F1-F2 из двух фазных напряжений фаз F1 и F2. Напряжение фаз F1 и F2 измеряется относительно нулевого провода. Линейное напряжение F1-F2 измеряется между двумя разными фазными проводами.

Как видим, что действующее межфазное напряжение больше амплитуды синусоидального напряжения одной фазы.

Амплитуда межфазного напряжения составляет:

Для наихудшего случая (сеть 240В и межфазное напряжение 415В, да еще 10% сверху) амплитуда межфазного напряжения составит:

Учтите это при работе в трехфазных сетях и выбирайте элементы, рассчитанные не менее, чем на 650В, если им предстоит работать между двумя фазами!

Надеюсь, теперь понятно что показывает вольтметр переменного тока?

Заключение

Итак, очень кратко, почти на пальцах, мы ознакомились с тем какие напряжения действуют в бытовых сетях переменного тока. Подведем краткие итоги всего, изложенного выше.

• Фазное напряжение — это напряжение между фазой и нулевым проводом.
• Линейное или межфазное напряжение — это напряжение между двумя разными фазными проводами одной трехфазной сети.
• В сетях переменного тока РФ действуют три, хоть и близких, но разных стандарта (фазное/линейное): 220В/380В, 230В/400В и 240В/415В переменного тока с частотой 50Гц.
• Вольтметр переменного тока обычно показывает действующее (оно же среднеквадратичное, оно же эффективное) напряжение, которое в раза меньше, чем пиковое (амплитудное) напряжение в сети.
• В наихудшем с точки зрения стандартов случае пиковое фазное напряжение составляет примерно 373В, а пиковое линейное напряжение — 645B. Это следует учитывать при разработке электронных схем.

Надеюсь эта статья помогла кому-то разобраться в теме и ответить для себя на некоторые вопросы.

Источник

Идеальный вольтметр

Cтраница 1

Идеальный вольтметр, включенный в электрическую цепь, показывает напряжение, равное разности потенциалов между точками подключения прибора.
 [2]

Идеальный вольтметр, не оказывающий возмущающего вотдейгтгшя на измеряемую цепь, должен обладать бесконечно большим сопротивлением или, скажем иначе, собственное потребление мощности ( от измеряемого объекта) вольтметром должно быть нулевым.
 [4]

Можете ли вы сказать, почему идеальный вольтметр должен иметь бесконечное сопротивление, а идеальный амперметр нулевое сопротивление.
 [5]

Ламповый вольтметр удовлетворяет всем требованиям, предъявляемым к идеальному вольтметру. Он измеряет напряжения, совершенно не потребляя тока. При этом становятся ненужными: декадные реостаты, измерительные мостики, нормальные элементы, капиллярный электрометр. Наряду с этим измерение, происходящее при действительном отсутствии тока ( в противоположность всем другим методам, при которых потребляется некоторое количество тока до окончательной компенсации), дает широкие возможности для усовершенствования электродов. Например, можно спокойно поворачивать краны электродов, если они не смазаны жиром, не вредя измерению. При помощи лампового вольтметра можно безупречно измерить даже рн воды для определения электропроводности — В случаях, когда можно опасаться отравления платинового электрода, ламповый вольтметр часто дает хорошие результаты, благодаря быстроте работы ( секунды), в то время как при старых методах никакие измерения здесь не были возможны.
 [6]

Требуется определить, как изменятся ( увеличатся или уменьшатся) показания всех идеальных вольтметров в цепи, показанной на рис. 77, если, например, уменьшить сопротивление R2 переменного резистора.
 [8]

Теперь начнем регулировать величины источников тока до тех: пор, пока напряжения, отмечаемые идеальными вольтметрами, не станут равными нулю. Легко заметить, что это должны быть токи, возникающие на соответствующих зажимах при одновременном коротком замыкании последних. Токи источников, подключен-ных к зажимам, должны скомпенсировать влияние источников, находящихся внутри ящика, в части их влияния на условия на зажимах.
 [9]

Поэтому вольтметр должен иметь большое сопротивление по сравнению с сопротивлением участка цепи, к которому он подключается. Идеальным вольтметром является такой, у которого сопротивление стремится к бесконечности.
 [10]

Составление неопределенной матрицы полезно, потому что упрощает получение уравнения полного передающего сопротивления от любой пары узлов цепи к любой другой паре узлов этой же цепи. Предположим, что источник тока присоединен между двумя узлами т и k, так что ток I, входит в г-й узел и выходит из fe-ro узла. Предположим также, что идеальный вольтметр ( имеющий бесконечно большое входное сопротивление) присоединен между узлами j и m и таким образом измеряет разность потенциалов между этими узлами.
 [11]

Страницы:  

   1

Приветствую всех, сегодня в рамках курса «Основы электроники» мы рассмотрим основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр и амперметр.

Измерение тока. Амперметр.

И начнем с измерения тока. Прибор, используемый для этих целей, называется амперметр, и в цепь он включается последовательно. Рассмотрим небольшой пример:

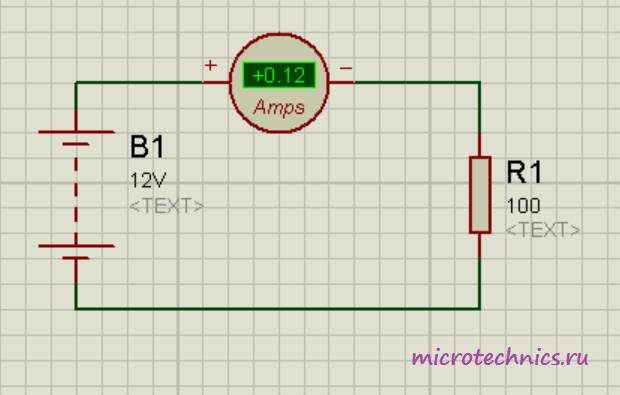
Как видите, здесь источник питания подключен напрямую к резистору, символизирующему полезную нагрузку. Кроме того, в цепи присутствует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи:

I = frac{U}{R} = frac{12}{100} = 0.12

Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи 👍

Важным параметром этого прибора является его внутреннее сопротивление r_А. Почему это так важно? Смотрите сами — при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится общее сопротивление, и мы получим следующее значение:

Если бы амперметр был абсолютно идеальным, и его сопротивление равнялось нулю, то он бы не оказал никакого влияния на работу электрической цепи, параметры которой необходимо измерить, но на практике все не совсем так, и сопротивление прибора не равно 0. Конечно, сопротивление амперметра достаточно мало (поскольку производители стремятся максимально его уменьшить), поэтому во многих примерах и задачах им пренебрегают, но не стоит забывать, что оно все-таки и есть и оно ненулевое.

При разговоре об измерении силы тока невозможно не упомянуть о способе, который позволяет расширить пределы, в которых может работать амперметр. Этот метод заключается в том, что параллельно амперметру включается шунт (резистор), имеющий определенное сопротивление:

R = frac{r_А}{nmedspace-medspace 1}

В этой формуле n — это коэффициент шунтирования — число, которое показывает во сколько раз будут увеличены пределы, в рамках которых амперметр может производить свои измерения. Возможно это все может показаться не совсем понятным и логичным, поэтому сейчас мы рассмотрим практический пример, который позволит во всем разобраться.

Пусть максимальное значение, которое может измерить амперметр составляет 1 А. А схема, силу тока в которой нам нужно определить имеет следующий вид:

Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Напряжение в 1200 В взято исключительно ради примера, сокровенного практического смысла в этом нет ) Итак, из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:

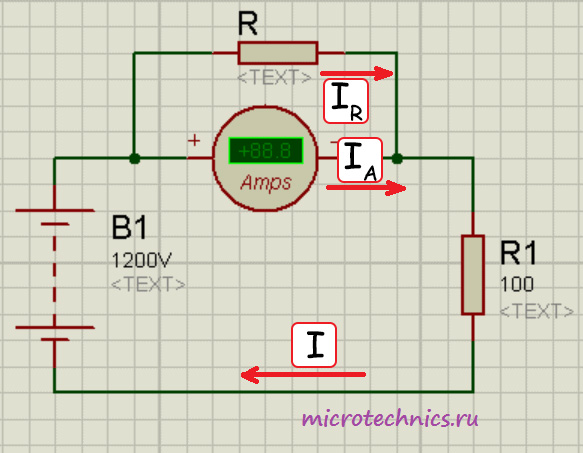
В данной задаче нам необходимо измерить ток I. Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и получим нужное значение. Для реализации задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:

R = frac{r_А}{nmedspace-medspace 1}

В данном случае n = 25, но мы проведем все расчеты в общем виде, чтобы показать, что величины могут быть абсолютно любыми, принцип шунтирования будет работать одинаково.

Итак, поскольку напряжения на шунте и на амперметре равны, мы можем записать первое уравнение:

I_Аmedspace r_А = I_Rmedspace R

Выразим ток шунта через ток амперметра:

I_R = I_Аmedspace frac{r_А}{R}

Измеряемый ток равен:

Подставим в это уравнение предыдущее выражение для тока шунта:

I = I_А + I_Аmedspace frac{r_А}{R}

Но сопротивление шунта нам также известно (R = frac{r_А}{nmedspace-medspace 1}). В итоге мы получаем:

I = I_Аmedspace (1 + frac{r_Аmedspace (nmedspace-medspace 1)}{r_А}enspace) = I_Аmedspace n

Вот мы и получили то, что и хотели. Значение, которое покажет амперметр в данной цепи будет в n раз меньше, чем сила тока, величину которой нужно измерить.

С измерениями тока в цепи все понятно, давайте перейдем к следующему вопросу, а именно определению напряжения.

Измерение напряжения. Вольтметр.

Прибор, предназначенный для измерения напряжения, называется вольтметр. И, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся, с чем это связано:

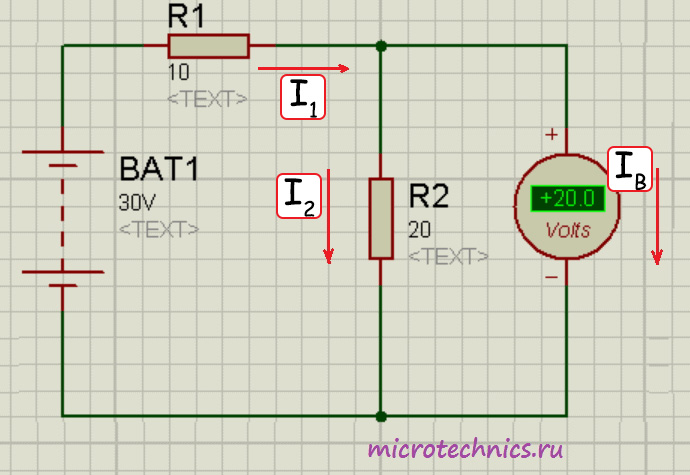
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:

I_1 = I_2 = frac{U}{R_1 + R_2} = frac{30}{10 + 20} = 1

Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с R_2. Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (I_B = 0), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку r_В имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток. В связи с этим напряжение на резисторе R_2 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.

Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:

R_Д = r_Вmedspace (nmedspace-medspace 1)

Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример:

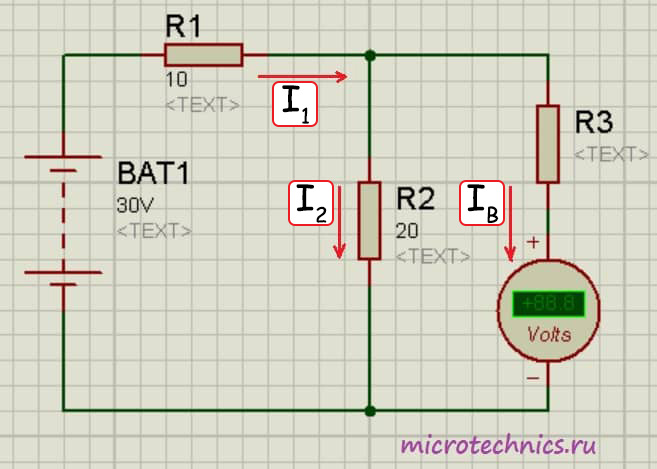
Здесь мы добавили в цепь добавочное сопротивление R_3. Перед нами стоит задача измерить напряжение на резисторе R_2:medspace U_2 = R_2medspace I_2. Давайте определим, какой результат при таком включении выдаст нам вольтметр:

U_2 = I_2medspace R_2 = U_В + I_Вmedspace R_3

Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:

U_2 = U_В + I_Вmedspace (r_Вmedspace (nmedspace-medspace 1)) = U_В + I_Вmedspace r_Вmedspace nmedspace-medspace I_Вmedspace r_В = U_В + U_Вmedspace nmedspace-medspace U_В = U_Вmedspace n

Таким образом: U_В = frac{U_2}{n}. То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно значительно увеличить пределы измерения вольтметра.

В завершении статьи пару слов об измерении сопротивления и мощности.

Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи (омметр) и мощности (ваттметр).

В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями!