Цели:
-
получить
представление о типах последовательностей
и способах их обработки; -
освоить методику
написания циклических вычислительных
алгоритмов для вычисления
последовательностей, перевода таких
алгоритмов на язык программирования
С++ и разработки соответствующего
проекта в среде Visual
C++
6.0.
Циклические
структуры используются для вычисления
элементов рекуррентных последовательностей,
обработки массивов, а также решения
задач, которые предполагают использование
численных методов.
4. Примеры вычисления последовательностей
-
Пусть переменная
х принимает
последовательно значения х1,х2,х3, … ,хn,
… .Такое
нумерованное множество чисел называется
последовательностью. Закон образования
последова-тельности задается формулой
n-гочлена
хn.
Из данного
определения видно, что для задания
последовательности нужно знать закон
образования n—го
члена последовательности, т.е. функцию,
которая ставит натуральному числу n
в соответствие некоторое значение f(n):
xn=f(n).
-
Последовательность
{xn}
называется сходящейся к х*,
если при n→ ∞
|x*—xn|→0. -
Последовательность
{xn}
называется убывающей, если при n→
∞ |xn|→0. -
Последовательность
{xn}
называется возрастающей, если при n→
∞ |xn|→∞.
При вычислении
возрастающих последовательностей
должно быть задано условие, ограничивающее
вычисление элементов такой
последовательности.
-
Пусть дана
некоторая последовательность элемент-ов
а1,а2,
а3, … , аn,…,
причём ак+1=F(а1,
а2,… аn,
ак), ак+2=F(а2,а3,…аn,
ак, ак+1).Если функцию F
можно определить или она задана, то
последовательность а1,
а2, а3, … , ак,
ак+1, …называется
рекуррентной последовательностью.
Формула n-го
члена рекуррентной последовательности
(рекуррентная формула) аn=F(an—k
,an—k+1,аn-к+2,…,аn-1),
где число kназывается глубиной
рекурсии и определяет количество
предшествующих элементов, необходимых
для вычисления аn.
Смысл глубины рекурсии в том, что она
показывает, сколько переменных необходимо
для вычисления элементов последовательности.
Примеры задач с
использованием
рекуррентных
последовательностей
Вычислить заданный
n-й
элемент последовательности.
Вычислить сумму
или произведение n
элементов последовательности.
Найти количество
элементов на данном отрезке
последовательности, удовлетворяющих
определенному условию.
Найти номер первого
элемента последовательности,
удовлетворя-ющего определённому условию.
Пример 1.
Вычислить n-й
элемент арифметической прогрессии
а1=1, а2=3,
а3=5 и
т.д.
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Выведем рекуррентную
формулу. Так как разность прогрессии
равна 2, то
рекуррентная формула будет следующей:
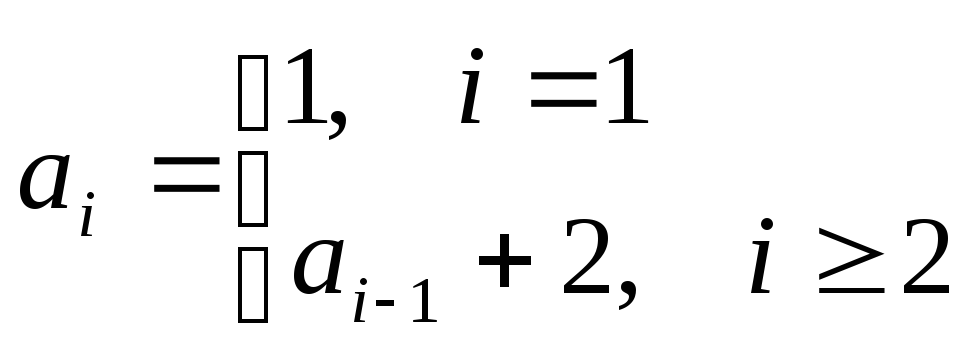
Читается формула так: приi=1
ai=1;
при i≥2
ai=ai—1+2,
т.е. каждый последующий элемент равен
сумме предыдущего и 2.
О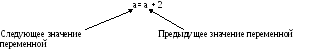
глубину рекурсии. Поскольку каждый
следующий элемент вычисляется только
через один предыдущий, то глубина
рекурсии равна 1.
Следовательно, для вычисления элементов
последовательности нужны две переменные.
Однако в этом случае можно обойтись
одной переменной. Для определения
значения последующего элемента
последовательности будем использовать
рекурсивную формулу
-
Алгоритм
Программа
объявление цел: а,n,i
ввод n
//текущий элемент последовательности
и //его текущий номера=1,i=1
//вычисляем элементы последовательности
для i=2 доnшаг 1
а=а+2
всё_для i
печать а
#include «stdio.h»
#include «math.h»
int main ( )
{
int a, i, n;
printf(«n=»);
scanf(«%i»,&n);
a=1,i=1;
for (i=2;i<=n;i++)
a=a+2;
printf(«a%i=%i n»,n,a);
return 1;
}
Написать программу,
соответствующую алгоритму: -
Создать проект
и реализовать данную задачу в среде
Visual
C++
6.0.
Пример 2.
Вывести на печать первые n
(n≥3)
чисел Фибоначчи. Распечатать все элементы
и подсчитать, сколько среди них четных
чисел. Числа Фибоначчи образуются по
закону:
а1=1, а2=1, … ,
аi=ai-1+ai-2,
….
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Рекуррентная
формула задается в определении чисел
Фибоначчи:
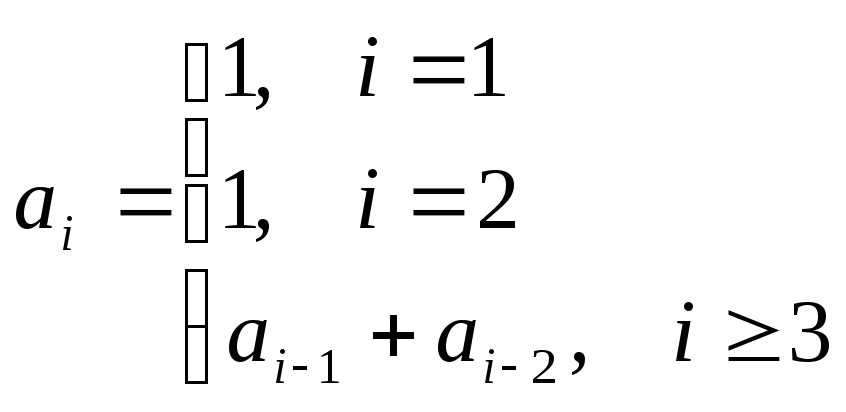
Глубина рекурсии
равна 2, поэтому
для вычисления чисел Фибоначчи нужны
три переменные.
-
Написать программу,
соответствующую алгоритму:
|
Алгоритм |
Программа |
|
объявление цел: i,n,a1,a2, а3,s //ввод количества вычисляемых элементов ввод n //инициализация а1=1, а2=1, s=0 печать а1 печать а2 //цикл для вычисления элементов и суммы для i=3 доnшаг 1 a3=a2+a1 печать а3 если а2%2=0 //условие четности
//значения переменной s=s+1 все_если а1=a2 а2=а3 всё_для i печать s |
#include «stdio.h» #include «math.h» int main ( ) { int a1, a2, a3, s, i, n; printf(«n=»); scanf(«%i»,&n); a1=1, a2=1, s=0; printf(«a1=%in», a1); printf(«a2=%in», a2); for (i=3;i<=n;i++) { a3=a2+a1; printf(«a%i=%i n», i, a3); if(a2%2==0) s=s+1; a1=a2; a2=a3; } printf(«s=%i n», s); return 1; } |
П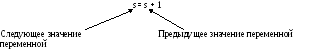
В алгоритме использована рекурсивная
формула
-
Создать проект и
реализовать данную задачу в среде
Visual
C++
6.0.
Последовательности
в примерах 1 и 2 являются возрастающими,
поэтому вычисление элементов ограничивается
заданием их количества.
Пример 3.
Для заданных действительного x
и целого n
вычислить сумму
.
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Формула для
вычисления суммы:
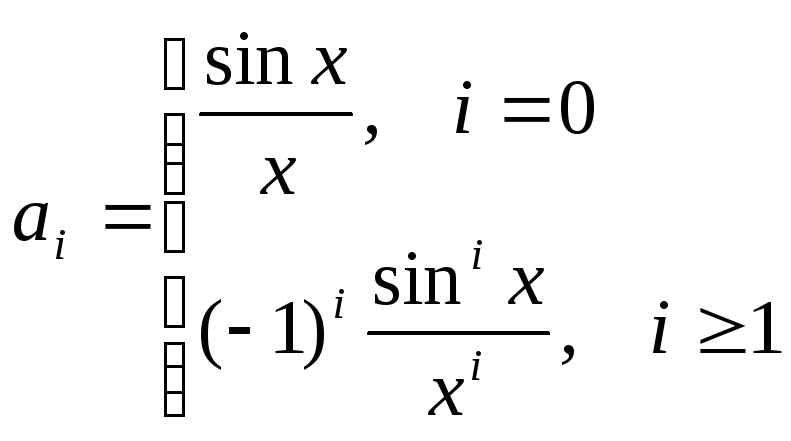
Здесь i
обозначает номер текущего элемента
последовательности, n
– количество элементов последовательности,
сумму которых нужно вычислить.
Глубина рекурсии
в данном случае не определяется, так
как данная формула не является
рекуррентной.
-
Написать программу,
соответствующую алгоритму6
|
Алгоритм |
Программа |
|
Объявление цел: i,n; //ввод количества элементов ввод n ввод x
//начальное значение номера элемента i=0 //начальное значение элемента // последовательности а=sin(x)/x
//начальное значение суммы элементов s=a
//цикл для вычисления элементов и суммы для i=1 доnшаг 1 a= (-1)isini(x)/xi s=s+a всё_для i //вывод полученной суммы на экран печать s |
#include «stdio.h» #include «math.h» int main ( ) { int i, n; float x, s, a; printf(«n=»); scanf(«%i»,&n); printf(«x=»); scanf(«%f»,&x); // инициализация переменных i=0; a=sin(x)/x; s=0;
//цикл для вычисления элементов и for (i=1;i<=n;i++) { a=pow(-1,i)*pow(sin(x),i)/pow(x,i); s=s+a; } //вывод полученной суммы на экран printf(«s=%f n», s); return 1; } |
Примечание.
В алгоритме использована рекурсивная
формула
-
Создать проект и
реализовать данную задачу в среде
Visual
C++
6.0.
Пример 4.
Для заданного вещественного х
и малой величины eps
вычислить сумму ряда
.
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Рекуррентная
формула выводится из предположения,
что слагаемые ряда являются членами
бесконечно
убывающей
геометрической прогрессии. Пусть
.
Таким образом, рекуррентная формула
выглядит следующим образом:
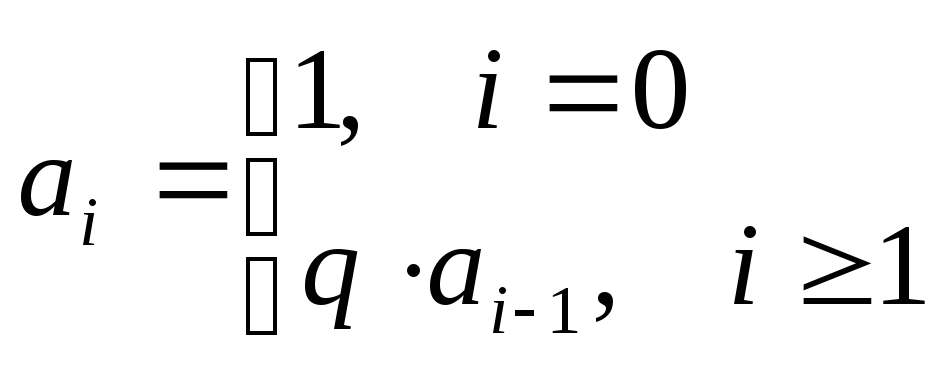
где
.
Формула дляберется из формулы ряда
.
Для нахождения формулыподставим в формулу
i-1вместо
i:
.
Для вычисления q
необходимо
знать, что есть факториал числа.
Факториалом числа i
называют произведение последовательных
натуральных чисел от 1
до i
включительно, т.е. i!= 1·2·3·…·(i-1)·i.
Следовательно,
(2i-1)!
= 1·2·3·…·(2i-1),
а
(2i+1)!
= 1·2·3·…·(2i-1)·2i·(2i+1).
Вычислим
.
Получим рекуррентную формулу

При записи этой
формулы наиболее частой ошибкой является
следующая
запись этой формулы:
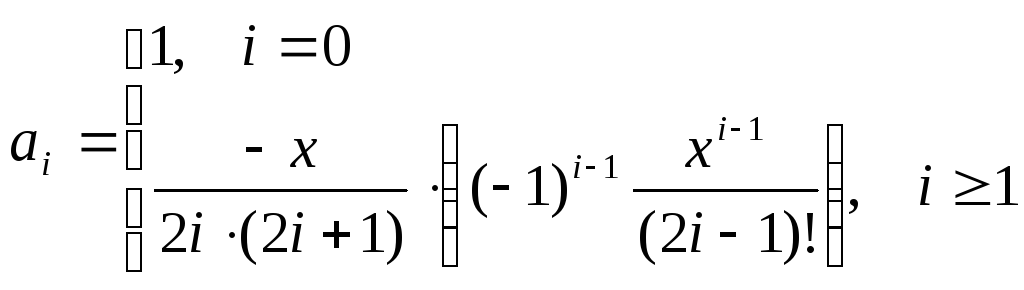
Эта формула не
будет являться рекуррентной, так как в
ней нет зависимости последующего
элемента последовательности от
предыдущего, следовательно, нет
возможности применить стандартный
алгоритм вычисления элементов и суммы
этих элементов (описание см. ниже).
Глубина рекурсии
равна 2, т.е.
для вычисления элементов последовательности
требуются две переменные. Как и в примере
1, обойдемся одной переменной.
Примечание.
При вычислении суммы ряда решающую роль
играет величина eps.
Она задаётся для того, чтобы ограничивать
количество вычисляемых элементов
последовательности, добавляемых в
сумму. При вычислении каждого элемента
последовательности его модуль сравнивается
с eps.
Если он больше eps,
то вычисления продолжаются, в противном
случае вычисление элементов
последовательности и добавление их в
искомую сумму прекращается. Такой
процесс называется вычислением суммы
ряда с точностью eps.
В качестве значения переменной eps
можно взять 0,001
или 0,00001 и т.п.
-
Написать программу,
соответствующую алгоритму:Алгоритм
Программа
Объявление вещ: х, eps,S,a, цел:i
ввод х, eps
//начальное значение номера элемента
//последовательностиi=0
//начальное значение элемента
//последовательностиa=1
//начальное значение суммы элементов
//последовательностиs=a
//цикл для вычисления элементов и
//суммы последовательностипокa|a|>=eps
//увеличиваем номер элемента
i=i+1
//вычисляем
новый элементa=a*(-x)/(2*i*(2*i+1))
//добавляем его в сумму
s=s+a
все_цикл
печать s
#include «stdio.h»
#include «math.h»
int main ( )
{
int i;
float x, eps, a, s;
printf(«x=»); scanf(«%f»,&x);
printf(«eps=»); scanf(«%f»,&eps);
// инициализация переменных
i=0;
a=1;
s=a;
//цикл для вычисления элементов и
//суммы последовательностиwhile (fabs(a)>=eps)
{
i=i+1;
a=a*(-x)/(2*i*(2*i+1));
s=s+a;
}
//вывод полученной суммы на экран
printf(«S=%f n»,s);
return 1;
}
-
Создать проект и
реализовать данную задачу в среде
Visual
C++
6.0.
Пример 5. Найти
наименьший номер члена последовательности,
для которого выполняется условие
.
Вывести на экран номер и все элементы,
где. Последовательность задается формулой
.
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Формула для
вычисления элементов последовательности:
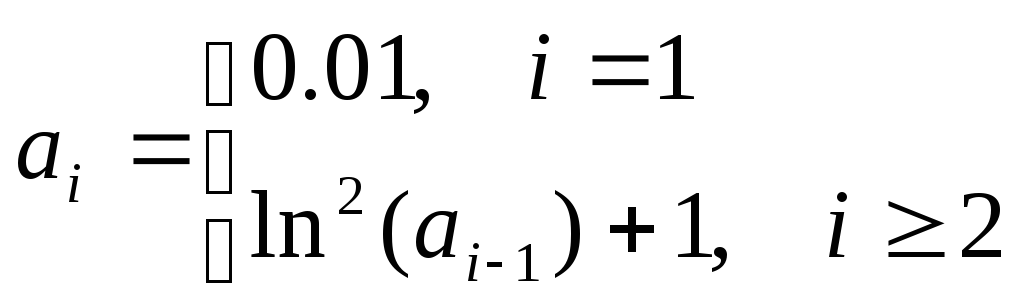
где i
– номер текущего элемента последовательности.
Глубина рекурсии
в данном случае равна 1,
т.е. для вычисления элементов
последовательности нужны две переменные.
-
Написать программу,
соответствующую алгоритму:Алгоритм
Программа
Объявление цел: i; вещ:
аt,ap,epsввод eps
//номер элемента равен 1
i=1
// текущий элемент
аt=0.01
печать at
//номер элемента увеличивается на 1
i++
// новый элемент
ap=ln2(at)+1
печать ap
// цикл для вычисления элементов
//последовательности
пока |at-ap|>=eps
//номер элемента увеличивается на 1
i++
//последующий элемент становится
//текущимat=ap
//вычисляется последующий элемент
ap=ln2(at)+1
печать ap
всё_цикл
печать i
#include «stdio.h»
#include «math.h»
int main ( )
{
int i;
float at, ap, eps;
printf(«eps=»);
scanf(«%f»,&eps);
i=1;
at=0.01;
printf(«a%i=%fn»,i, at);
i++;
ap=pow(log(at),2)+1;
printf(«a%i=%fn»,i, ap);
// цикл для вычисления элементов
//последовательности
while(fabs(at-ap)>=eps)
{
i++;
at=ap;
ap=pow(log(at),2)+1;
printf(«a%i=%fn»,i, ap);
}
printf(«min №=%i n», i);
return 1;
}
-
Создать проект и
реализовать данную задачу в среде
Visual
C++
6.0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найти наименьший номер последовательности, заданной рекуррентной формулой,
для которого выполняется условие |an — an-1l < e. Здесь e — малая величина.
Вывести на экран этот номер и все элементы ai, где i = 1,2, …, n.
an=2+a2n-1,a1=2
———————————————————————
2an-1
Это черта дроби, они идет после равно an
Код к задаче: «Найти наименьший номер последовательности, заданной рекуррентной формулой»
|
0 / 0 / 0 Регистрация: 08.05.2016 Сообщений: 29 |
|
|
1 |
|
найти наименьший номер элемента последовательности для которого выполняется условие06.11.2019, 23:38. Показов 3100. Ответов 3
Прошу помощи. никак не могу найти решения данной задачи. Кому не трудно прошу, помогите решить. Миниатюры
Изображения
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
06.11.2019, 23:38 |
|
3 |
|
SoBadDay 67 / 42 / 30 Регистрация: 26.03.2019 Сообщений: 269 |
||||
|
07.11.2019, 09:20 |
2 |
|||
|
daidara2512,
1 |
|
7427 / 5021 / 2891 Регистрация: 18.12.2017 Сообщений: 15,694 |
|
|
07.11.2019, 16:07 |
3 |
|
SoBadDay, по условию n не задано, поэтому в программе вводиться не может daidara2512, посмотрите тему:
1 |
|
0 / 0 / 0 Регистрация: 08.05.2016 Сообщений: 29 |
|
|
08.11.2019, 20:15 [ТС] |
4 |
|
Спасибо большое. Все отлично работает. Чутка переделал программу под себя.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
08.11.2019, 20:15 |
|
4 |
Только, наверное, не определение последовательности, а определение предела последовательности.
Число А — предел последовательности y = x(n), если для любого e > 0 существует такое N, что при любом n > N выполнено:
|x(n) — A| < e
У тебя последовательность y = (n+1)/(1-2n) = (n+1)/(-2n+1)
Идем строго по определению. Пусть у нас есть какое-то маленькое положительное число e > 0.
Нам надо доказать, что А = -1/2 — предел этой последовательности.
Для этого надо найти N — наименьший номер последовательности, такой, что для всех номеров n > N выполнено:
|x(n) — A| < e
А для всех номеров n <= N выполнено:
|x(n) — A| >= e
То есть нам надо решить систему неравенств:
{ |x(n-1) — A| >= e
{ |x(n) — A| < e
Подставляем нашу формулу:
{ n/(-2(n-1)+1) >= e
{ (n+1)/(-2n+1) < e
Упростим 1 неравенство
{ n/(-2n+3) >= e
{ (n+1)/(-2n+1) < e
Делим в обоих неравенствах знаменатель на -2, то есть по сути умножаем оба неравенства на -2. При этом меняется знак.
{ n/(n-3/2) <= -2e
{ (n+1)/(n-1/2) > -2e
Выделяем целую часть в обоих неравенствах
{ 1 + 1,5/(n-1,5) <= -2e
{ 1 + 1,5/(n-0,5) > -2e
Разделим оба неравенства обратно на -2. При этом снова меняется знак.
{ -2 — 0,75/(n-1,5) >= e
{ -2 — 0,75/(n-0,5) < e
Оставляем с одной стороны дробь, а с другой все остальное.
{ -0,75/(n-1,5) >= 2 + e
{ -0,75/(n-0,5) < 2 + e
Переворачиваем дроби, при этом знаки опять меняются.
{ (n-1,5)/(-0,75) <= 1/(2+e)
{ (n-0,5)/(-0,75) > 1/(2+e)
Упрощаем, домножая на -0,75, при этом знаки снова меняются.
{ n-1,5 >= -0,75/(2+e)
{ n-0,5 < -0,75/(2+e)
Выражаем n через е.
{ n >= 1,5 — 0,75/(2+e)
{ n < 0,5 — 0,75/(2+e)
В примере e = 10^(-2) = 0,01.
{ n >= 1,5 — 0,75/2,01 ~ 1,12
{ n < 0,5 — 0,75/2,01 ~ 0,12
То есть точность в 0,01 обеспечивается уже с n = 1. Чувствую я, что где-то ошибся, а найти не могу. Может, кто подскажет?
|
2 / 2 / 0 Регистрация: 18.05.2018 Сообщений: 9 |
|
|
1 |
|
Найти наименьший номер последовательности, заданной рекуррентной формулой18.05.2018, 21:14. Показов 10733. Ответов 1
Найти наименьший номер последовательности, заданной рекуррентной формулой, an=2+a2n-1,a1=2 Это черта дроби, они идет после равно an
__________________ 0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
18.05.2018, 21:14 |
|
1 |
|
Puporev Почетный модератор 64273 / 47572 / 32739 Регистрация: 18.05.2008 Сообщений: 115,182 |
||||
|
18.05.2018, 21:29 |
2 |
|||
|
Решение
0 |
Информатика,
вопрос задал dontTryAgainPls,
5 лет назад
Приложения:

На этот вопрос еще никто не ответил. Напишите свой ответ или воспользуйтесь поиском:
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика,
7 месяцев назад
Решите срочно!!!!!!
корень (5-3у) (3у-5) help meeeeeee…
Литература,
5 лет назад
Лист до Катерини» звертається до героїні поеми Т.Г.Шевченка.
Биология,
5 лет назад
5. По відношенню до води рослини поділяють на: А світлолюбні, тіньовитривалі, тіньолнoбні Б посухостійкі, помірно вологолюбні, вологолюбні, водні В холодовитривалі, теплошобні…
История,
6 лет назад
В какие годы жили правители Древнего Египта Тутмос и Хеопс ? (есть вариант что они жили в разное время )…
Математика,
6 лет назад
Решите уравнение икс минус 174=206…
Цели:
-
получить
представление о типах последовательностей
и способах их обработки; -
освоить методику
написания циклических вычислительных
алгоритмов для вычисления
последовательностей, перевода таких
алгоритмов на язык программирования
С++ и разработки соответствующего
проекта в среде Visual
C++
6.0.
Циклические
структуры используются для вычисления
элементов рекуррентных последовательностей,
обработки массивов, а также решения
задач, которые предполагают использование
численных методов.
4. Примеры вычисления последовательностей
-
Пусть переменная
х принимает
последовательно значения х1,х2,х3, … ,хn,
… .Такое
нумерованное множество чисел называется
последовательностью. Закон образования
последова-тельности задается формулой
n-гочлена
хn.
Из данного
определения видно, что для задания
последовательности нужно знать закон
образования n—го
члена последовательности, т.е. функцию,
которая ставит натуральному числу n
в соответствие некоторое значение f(n):
xn=f(n).
-
Последовательность
{xn}
называется сходящейся к х*,
если при n→ ∞
|x*—xn|→0. -
Последовательность
{xn}
называется убывающей, если при n→
∞ |xn|→0. -
Последовательность
{xn}
называется возрастающей, если при n→
∞ |xn|→∞.
При вычислении
возрастающих последовательностей
должно быть задано условие, ограничивающее
вычисление элементов такой
последовательности.
-
Пусть дана
некоторая последовательность элемент-ов
а1,а2,
а3, … , аn,…,
причём ак+1=F(а1,
а2,… аn,
ак), ак+2=F(а2,а3,…аn,
ак, ак+1).Если функцию F
можно определить или она задана, то
последовательность а1,
а2, а3, … , ак,
ак+1, …называется
рекуррентной последовательностью.
Формула n-го
члена рекуррентной последовательности
(рекуррентная формула) аn=F(an—k
,an—k+1,аn-к+2,…,аn-1),
где число kназывается глубиной
рекурсии и определяет количество
предшествующих элементов, необходимых
для вычисления аn.
Смысл глубины рекурсии в том, что она
показывает, сколько переменных необходимо
для вычисления элементов последовательности.
Примеры задач с
использованием
рекуррентных
последовательностей
Вычислить заданный
n-й
элемент последовательности.
Вычислить сумму
или произведение n
элементов последовательности.
Найти количество
элементов на данном отрезке
последовательности, удовлетворяющих
определенному условию.
Найти номер первого
элемента последовательности,
удовлетворя-ющего определённому условию.
Пример 1.
Вычислить n-й
элемент арифметической прогрессии
а1=1, а2=3,
а3=5 и
т.д.
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Выведем рекуррентную
формулу. Так как разность прогрессии
равна 2, то
рекуррентная формула будет следующей:
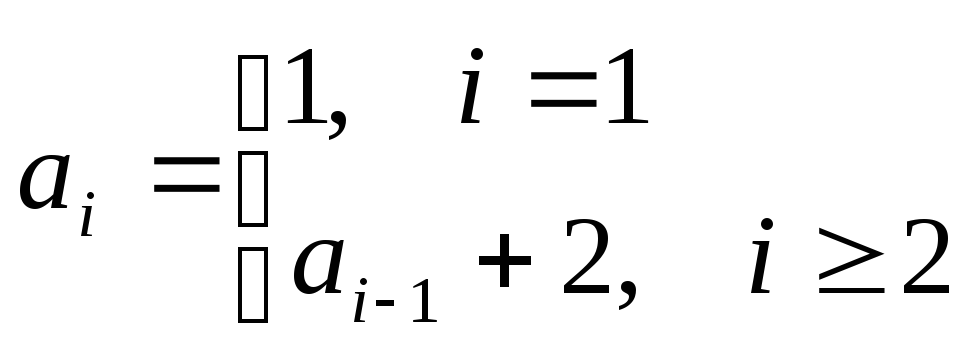
Читается формула так: приi=1
ai=1;
при i≥2
ai=ai—1+2,
т.е. каждый последующий элемент равен
сумме предыдущего и 2.
О
глубину рекурсии. Поскольку каждый
следующий элемент вычисляется только
через один предыдущий, то глубина
рекурсии равна 1.
Следовательно, для вычисления элементов
последовательности нужны две переменные.
Однако в этом случае можно обойтись
одной переменной. Для определения
значения последующего элемента
последовательности будем использовать
рекурсивную формулу
-
Алгоритм
Программа
объявление цел: а,n,i
ввод n
//текущий элемент последовательности
и //его текущий номера=1,i=1
//вычисляем элементы последовательности
для i=2 доnшаг 1
а=а+2
всё_для i
печать а
#include «stdio.h»
#include «math.h»
int main ( )
{
int a, i, n;
printf(«n=»);
scanf(«%i»,&n);
a=1,i=1;
for (i=2;i<=n;i++)
a=a+2;
printf(«a%i=%i n»,n,a);
return 1;
}
Написать программу,
соответствующую алгоритму: -
Создать проект
и реализовать данную задачу в среде
Visual
C++
6.0.
Пример 2.
Вывести на печать первые n
(n≥3)
чисел Фибоначчи. Распечатать все элементы
и подсчитать, сколько среди них четных
чисел. Числа Фибоначчи образуются по
закону:
а1=1, а2=1, … ,
аi=ai-1+ai-2,
….
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Рекуррентная
формула задается в определении чисел
Фибоначчи:
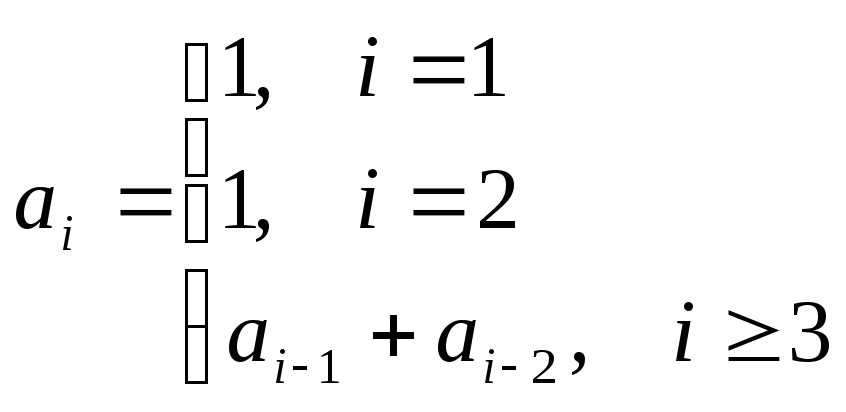
Глубина рекурсии
равна 2, поэтому
для вычисления чисел Фибоначчи нужны
три переменные.
-
Написать программу,
соответствующую алгоритму:
|
Алгоритм |
Программа |
|
объявление цел: i,n,a1,a2, а3,s //ввод количества вычисляемых элементов ввод n //инициализация а1=1, а2=1, s=0 печать а1 печать а2 //цикл для вычисления элементов и суммы для i=3 доnшаг 1 a3=a2+a1 печать а3 если а2%2=0 //условие четности
//значения переменной s=s+1 все_если а1=a2 а2=а3 всё_для i печать s |
#include «stdio.h» #include «math.h» int main ( ) { int a1, a2, a3, s, i, n; printf(«n=»); scanf(«%i»,&n); a1=1, a2=1, s=0; printf(«a1=%in», a1); printf(«a2=%in», a2); for (i=3;i<=n;i++) { a3=a2+a1; printf(«a%i=%i n», i, a3); if(a2%2==0) s=s+1; a1=a2; a2=a3; } printf(«s=%i n», s); return 1; } |
П
В алгоритме использована рекурсивная
формула
-
Создать проект и
реализовать данную задачу в среде
Visual
C++
6.0.
Последовательности
в примерах 1 и 2 являются возрастающими,
поэтому вычисление элементов ограничивается
заданием их количества.
Пример 3.
Для заданных действительного x
и целого n
вычислить сумму
.
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Формула для
вычисления суммы:
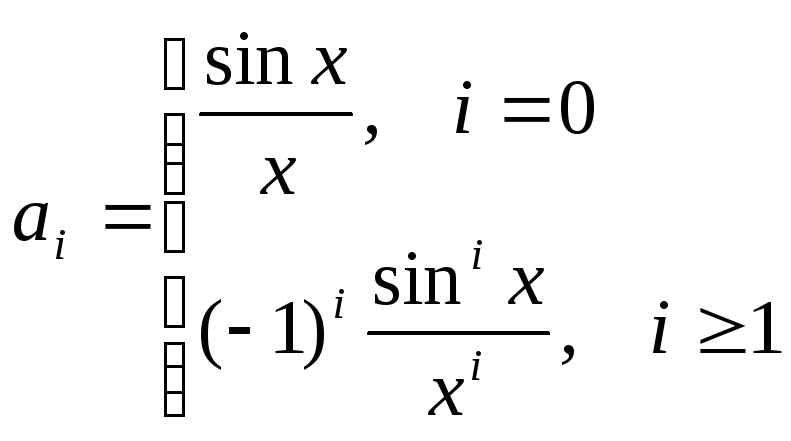
Здесь i
обозначает номер текущего элемента
последовательности, n
– количество элементов последовательности,
сумму которых нужно вычислить.
Глубина рекурсии
в данном случае не определяется, так
как данная формула не является
рекуррентной.
-
Написать программу,
соответствующую алгоритму6
|
Алгоритм |
Программа |
|
Объявление цел: i,n; //ввод количества элементов ввод n ввод x
//начальное значение номера элемента i=0 //начальное значение элемента // последовательности а=sin(x)/x
//начальное значение суммы элементов s=a
//цикл для вычисления элементов и суммы для i=1 доnшаг 1 a= (-1)isini(x)/xi s=s+a всё_для i //вывод полученной суммы на экран печать s |
#include «stdio.h» #include «math.h» int main ( ) { int i, n; float x, s, a; printf(«n=»); scanf(«%i»,&n); printf(«x=»); scanf(«%f»,&x); // инициализация переменных i=0; a=sin(x)/x; s=0;
//цикл для вычисления элементов и for (i=1;i<=n;i++) { a=pow(-1,i)*pow(sin(x),i)/pow(x,i); s=s+a; } //вывод полученной суммы на экран printf(«s=%f n», s); return 1; } |
Примечание.
В алгоритме использована рекурсивная
формула
-
Создать проект и
реализовать данную задачу в среде
Visual
C++
6.0.
Пример 4.
Для заданного вещественного х
и малой величины eps
вычислить сумму ряда
.
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Рекуррентная
формула выводится из предположения,
что слагаемые ряда являются членами
бесконечно
убывающей
геометрической прогрессии. Пусть
.
Таким образом, рекуррентная формула
выглядит следующим образом:
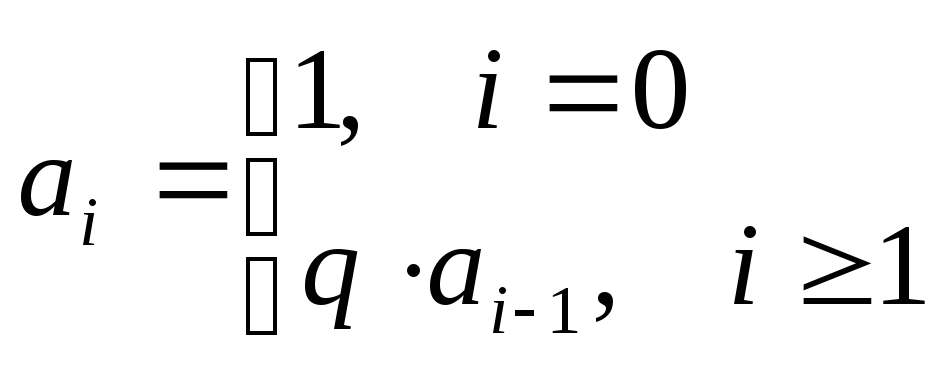
где
.
Формула дляберется из формулы ряда
.
Для нахождения формулыподставим в формулу
i-1вместо
i:
.
Для вычисления q
необходимо
знать, что есть факториал числа.
Факториалом числа i
называют произведение последовательных
натуральных чисел от 1
до i
включительно, т.е. i!= 1·2·3·…·(i-1)·i.
Следовательно,
(2i-1)!
= 1·2·3·…·(2i-1),
а
(2i+1)!
= 1·2·3·…·(2i-1)·2i·(2i+1).
Вычислим
.
Получим рекуррентную формулу

При записи этой
формулы наиболее частой ошибкой является
следующая
запись этой формулы:
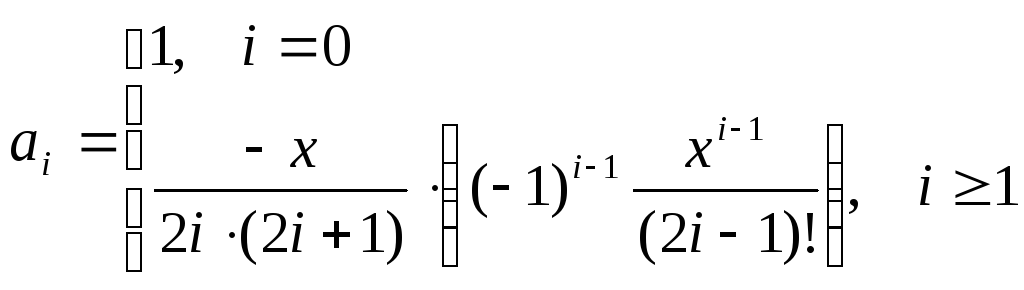
Эта формула не
будет являться рекуррентной, так как в
ней нет зависимости последующего
элемента последовательности от
предыдущего, следовательно, нет
возможности применить стандартный
алгоритм вычисления элементов и суммы
этих элементов (описание см. ниже).
Глубина рекурсии
равна 2, т.е.
для вычисления элементов последовательности
требуются две переменные. Как и в примере
1, обойдемся одной переменной.
Примечание.
При вычислении суммы ряда решающую роль
играет величина eps.
Она задаётся для того, чтобы ограничивать
количество вычисляемых элементов
последовательности, добавляемых в
сумму. При вычислении каждого элемента
последовательности его модуль сравнивается
с eps.
Если он больше eps,
то вычисления продолжаются, в противном
случае вычисление элементов
последовательности и добавление их в
искомую сумму прекращается. Такой
процесс называется вычислением суммы
ряда с точностью eps.
В качестве значения переменной eps
можно взять 0,001
или 0,00001 и т.п.
-
Написать программу,
соответствующую алгоритму:Алгоритм
Программа
Объявление вещ: х, eps,S,a, цел:i
ввод х, eps
//начальное значение номера элемента
//последовательностиi=0
//начальное значение элемента
//последовательностиa=1
//начальное значение суммы элементов
//последовательностиs=a
//цикл для вычисления элементов и
//суммы последовательностипокa|a|>=eps
//увеличиваем номер элемента
i=i+1
//вычисляем
новый элементa=a*(-x)/(2*i*(2*i+1))
//добавляем его в сумму
s=s+a
все_цикл
печать s
#include «stdio.h»
#include «math.h»
int main ( )
{
int i;
float x, eps, a, s;
printf(«x=»); scanf(«%f»,&x);
printf(«eps=»); scanf(«%f»,&eps);
// инициализация переменных
i=0;
a=1;
s=a;
//цикл для вычисления элементов и
//суммы последовательностиwhile (fabs(a)>=eps)
{
i=i+1;
a=a*(-x)/(2*i*(2*i+1));
s=s+a;
}
//вывод полученной суммы на экран
printf(«S=%f n»,s);
return 1;
}
-
Создать проект и
реализовать данную задачу в среде
Visual
C++
6.0.
Пример 5. Найти
наименьший номер члена последовательности,
для которого выполняется условие
.
Вывести на экран номер и все элементы,
где. Последовательность задается формулой
.
Ход выполнения
работы
-
Написание алгоритма
решения задачи будет состоять из двух
шагов.
Формула для
вычисления элементов последовательности:
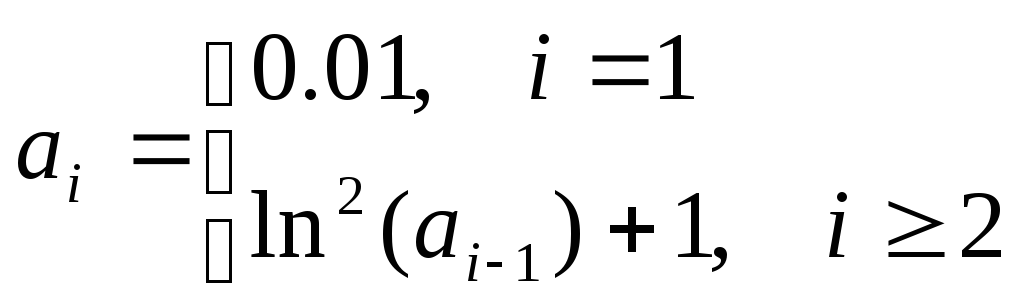
где i
– номер текущего элемента последовательности.
Глубина рекурсии
в данном случае равна 1,
т.е. для вычисления элементов
последовательности нужны две переменные.
-
Написать программу,
соответствующую алгоритму:Алгоритм
Программа
Объявление цел: i; вещ:
аt,ap,epsввод eps
//номер элемента равен 1
i=1
// текущий элемент
аt=0.01
печать at
//номер элемента увеличивается на 1
i++
// новый элемент
ap=ln2(at)+1
печать ap
// цикл для вычисления элементов
//последовательности
пока |at-ap|>=eps
//номер элемента увеличивается на 1
i++
//последующий элемент становится
//текущимat=ap
//вычисляется последующий элемент
ap=ln2(at)+1
печать ap
всё_цикл
печать i
#include «stdio.h»
#include «math.h»
int main ( )
{
int i;
float at, ap, eps;
printf(«eps=»);
scanf(«%f»,&eps);
i=1;
at=0.01;
printf(«a%i=%fn»,i, at);
i++;
ap=pow(log(at),2)+1;
printf(«a%i=%fn»,i, ap);
// цикл для вычисления элементов
//последовательности
while(fabs(at-ap)>=eps)
{
i++;
at=ap;
ap=pow(log(at),2)+1;
printf(«a%i=%fn»,i, ap);
}
printf(«min №=%i n», i);
return 1;
}
-
Создать проект и
реализовать данную задачу в среде
Visual
C++
6.0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


 Сообщение было отмечено needfortrane как решение
Сообщение было отмечено needfortrane как решение