Конусность — это отношение разности диаметров к длине(высоте) конуса. Например,
конусноть 1:10 означает, что D — d = 1, а L(h) = 10. А конусноть 7:24 означает, что D — d = 7, а L(h) = 24.

Конус — геометрическое тело, которое получается путем вращением прямой линии (образующей конуса),
расположенной под углом к оси вращения.
Конусность измерить нельзя. Измеряют угол, который соответсвует конкретной конусности. Например,
угол конусности 1 : 10 будет равен 5° 43′ 29.3″ (5 градусам 43 минутам 29.3 секундам). 1 угол содержит 60 минут, а 1 минута содержит 60 секунд.
На производстве углы измеряют инструментом, который называется угломер.
С помощью калькулятора на данной странице вы сможете рассчитать любую конусность.
Часто это бывает нужно, когда на чертеже не хватает размеров, а чертеж не в векторном формате.
Так же, например, необходима бывает индентификация конусности на существующем изделии (штифт, инструмент и др.).
Нормальные конусности представлены в ГОСТ 8593-81.
Инструментальные конусности представлены в ГОСТ 25557-2006. Среди инструментальных конусов
выделяются конуса Морзе. В российских стандартах обозначаются КМ0-КМ7 (КМ7 не рекомендован к применению). В немецких стандартах
МК0-МК7. В английских стандартах МТ0-МТ7.
При расчете используются следующие буквенные обозначения:
- D — наибольшее основание конуса;
- d — наименьшее основание конуса;
- L — длина конуса;
- α — угол конуса;
- α/2- угол уклона.
| Конусность | Угол конуса | Угол уклона |
|---|---|---|
| 1 : 500 | 0° 6′ 52.5″ | 0° 3′ 25.25″ |
| 1 : 200 | 0° 17′ 11.3″ | 0° 8′ 35.65″ |
| 1 : 100 | 0° 34′ 22.6″ | 0° 17′ 11.3″ |
| 1 : 50 | 1° 8′ 45.2″ | 0° 34′ 22.6″ |
| 1 : 30 | 1° 54′ 34.9″ | 0° 57′ 17.45″ |
| 1 : 20 | 2° 51′ 51.1″ | 1° 25′ 55.55″ |
| 1 : 15 | 3° 49′ 5.9″ | 1° 54′ 32.95″ |
| 1 : 12 | 4° 46′ 18.8″ | 2° 23′ 9.4″ |
| 1 : 10 | 5° 43′ 29.3″ | 2° 51′ 44.65″ |
| 1 : 8 | 7° 9′ 9.6″ | 3° 34′ 34.8″ |
| 1 : 7 | 8° 10′ 16.4″ | 4° 5′ 8.2″ |
| 1 : 6 | 9° 31′ 38.2″ | 4° 45′ 49.1″ |
| 1 : 5 | 11° 25′ 16.3″ | 5° 42′ 38.15″ |
| 1 : 4 | 14° 15′ 0.1″ | 7° 7′ 30.05″ |
| 1 : 3 | 18° 55′ 28.7″ | 9° 27′ 44.35″ |
| 1 : 1.866025 | 30° 0′ 0″ | 15° 0′ 0″ |
| 1 : 1.207107 | 45° 0′ 0″ | 22° 30′ 0″ |
| 1 : 0.866025 | 60° 0′ 0″ | 30° 0′ 0″ |
| 1 : 0.651613 | 75° 0′ 0″ | 37° 30′ 0″ |
| 1 : 0.500000 | 90° 0′ 0″ | 45° 0′ 0″ |
| 1 : 0.288675 | 120° 0′ 0″ | 60° 0′ 0″ |
| Метрический конус | ||
| 1 : 20 | 2° 51′ 51.1″ | 1° 25′ 55.55″ |
| Конус Морзе №0 | ||
| 1 : 19.212 | 1° 29′ 27″ | 0° 44′ 43.5″ |
| Конус Морзе №1 | ||
| 1 : 20.047 | 1° 25′ 43″ | 0° 42′ 51.5″ |
| Конус Морзе №2 | ||
| 1 : 20.020 | 1° 25′ 50″ | 0° 42′ 55″ |
| Конус Морзе №3 | ||
| 1 : 19.992 | 1° 26′ 16″ | 0° 43′ 8″ |
| Конус Морзе №4 | ||
| 1 : 19.254 | 1° 29′ 15″ | 0° 44′ 37.5″ |
| Конус Морзе №5 | ||
| 1 : 19.002 | 1° 30′ 26″ | 0° 45′ 13″ |
| Конус Морзе №6 | ||
| 1 : 19.18 | 1° 29′ 36″ | 0° 44′ 48″ |
| Конусность 7:24 | ||
| 1 : 3.42857143 | 16° 35′ 39″ | 8° 17′ 49″ |
| Конусность резьб конических | ||
| 1 : 16 | 3° 34′ 48″ | 1° 47′ 24″ |
Конус 1:500 и 1:200 применяют для изготовления крепежных деталей для неразъемных
соединений, подвергающихся вибрациям и ударной переменной нагрузке, конических оправок.
Конус 1:100 применяют для изготовления крепежных деталей для неразъемных
соединений, подвергающихся вибрациям и спокойной переменной нагрузке, клиновых шпонок, конических оправок.
Конус 1:50 применяют для изготовления конических штифтов, установочных шпилек,
насадных рукояток.
Конус 1:30 применяют для изготовления конусов шеек шпинделей.
Конус 1:20 применяют для изготовления метрических конусов в шпинделях станков, оправок.
Конус 1:16 применяют для изготовления конических резьбовых соединений метрических и дюймовых.
Конус 1:15 применяют для изготовления конических соединений деталей при осевых нагрузках,
соединений поршней со штоками.
Конус 1:12 применяют для изготовления конических закрепительных втолок шарико- и
роликоподшипников.
Конус 1:10 применяют для изготовления конических соединений деталей при нагрузках,
перпендикулярных и параллельных оси, концов валов электрических и других машин, регулируемых
втулок подшипников шпинделей.
Конус 1:7 применяют для кранов в арматуростроении.
Конус 1:5 и 1:3 применяют для изготовления легкоразъемных конических
соединений при нагрузках, перпендикулярных оси, конических фрикционных муфт.
Конус 1:1.5 применяют для изготовления тяжелых винтовых трубных соединений с коническим
уплотнением.
Конус 30° применяют для изготовления фрикционных муфт приводов, зажимных цанг,
головок шинных болтов.
Конус 60° применяют для изготовления центровых отверстий.
Конус 75° применяют для изготовления внутренних конусов нажимных гаек в соединениях труб
высокого давления, наружных центров инструментов диаметром до 10 мм.
Конус 90° применяют для изготовления концов обрабатываемых валов и валиков,
конусов вентилей и клапанов, центровых отверстий для тяжелых работ, потайных головок заклепок диаметром
1 — 10 мм.
Конус 100° применяют для изготовления винтов по дереву.
Конус 120° применяют для изготовления потайных головок заклепок диаметром
2 — 5 мм, внутренних фаскок резьбовых отверстий, конусов под набивку сальников, дроссельных клапанов.

Значок конуса обязательно должен быть направлен в сторону уменьшения диаметра.
Посмотреть какие настройки токарного станка для обработки конуса существуют
можно на этой странице .
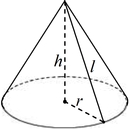
Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.
Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.
Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.
Радиус конуса – это радиус его основания.
Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Формула площади основания конуса
Площадь основания конуса можно вычислить по его радиусу R:
Sосн = πR2
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Формула объема конуса
Объем конуса можно вычислить, зная его высоту H и площадь основания:
V = 1/3 ⋅ Sосн ⋅ H = 1/3πR2H
Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая — директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
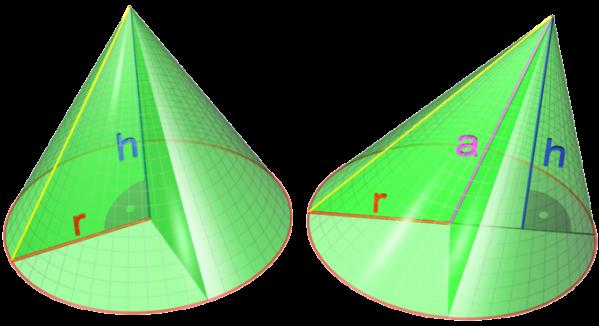
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.
Здесь r — радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая — это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
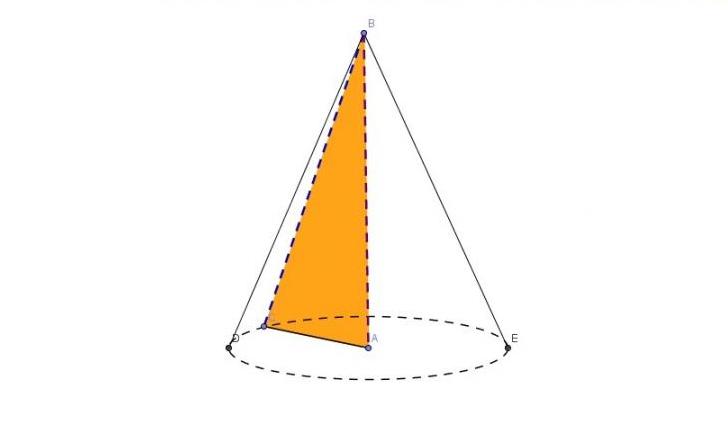
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 — h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Вычисление диаметра через площадь поверхности и генератрису
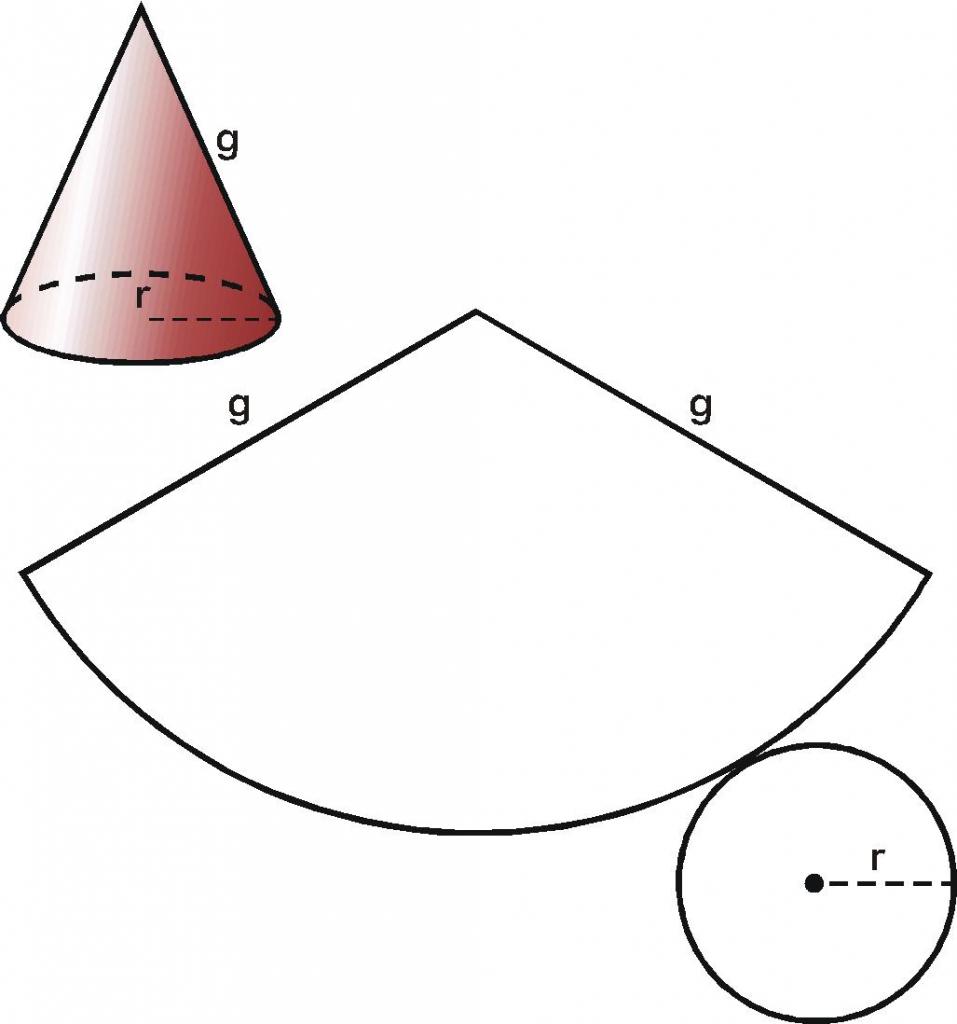
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
Общая площадь развертки определяется по следующей формуле:
S = pi*r2 + pi*r*g
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
V = 1/3*S*h
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
V = 1/3*pi*r2*h
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
r = √(3*V/(pi*h));
d = 2*r = 2*√(3*V/(pi*h))
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Задача на определение диаметра через известную площадь конуса и его образующую
Дан конус, площадь поверхности которого составляет 150 см2. Генератриса равна 14 см. Чему равен диаметр конуса?
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
S = pi*r2 + pi*r*g =>
r2 + 14*r — 150/3,14 = 0
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
D = 142 — 4*1*(-150/3,14) = 387,0828
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
r = (-14±√D)/2
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
r = (-14+√387,0828)/2 = 2,837 см
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.
Основание конуса — это его единственная круглая грань, самый широкий круг в стопке кругов, идущий вверх или вниз по длине конуса. Например, если вы наполнили конус мороженого, основание было бы его вершиной. Основание конуса — это круг, поэтому, если вы знаете радиус конуса, вы можете найти площадь основания, используя формулу площади для круга.
Радиус и Пи
Радиус, обычно обозначаемый как «r» конуса, представляет собой расстояние от центра основания конуса до стороны основания конуса. Pi определяется как окружность круга, деленная на его диаметр. Он всегда имеет одинаковое значение: примерно 3, 14. В зависимости от уровня точности, который вам нужен в ваших вычислениях, число pi может быть расширено до бесконечного числа цифр после десятичной точки. Например, число пи, расширенное до семи цифр, будет равно 3.1415926. Тем не менее, 3.14 считается достаточно хорошим приближением для основных геометрических уравнений.
Нахождение территории базы
Площадь круга, или A, и площадь основания конуса, равна pi, умноженному на его радиус в квадрате: A = pi xr ^ 2. Число в квадрате равно этому числу, умноженному на себя. Если бы ваш конус имел радиус 7 дюймов, вы бы вычислили площадь следующим образом: A = pi x 7 дюймов ^ 2 = 3, 14 x 7 дюймов x 7 дюймов = 153, 86 квадратных дюймов
Задание 8. Математика ЕГЭ. Найти объем меньшего конуса, основание которого сечение проведенное параллельно основанию большого конуса
Задание. Объем конуса равен 152. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение:
Объем большого конуса равен:
Vб = 1/3·π·R^2·H
Vм = 1/3·π·r^2·h (1)
Так как сечение проходит через середину высоты, то H = 2h, R = 2r.
Vб = 1/3·π·(2r)^2·2h
Vб = 1/3·8·π·r^2·h (2)
Найдем отношение (1) ко (2) формуле:
Vм/Vб = 1/8
Vм = 1/8·Vб
Vм = 1/8·152 = 19.
Ответ: 19.
Оставить комментарий
Рубрики
- Демоверсия ЕГЭ по информатике
- Демоверсия ЕГЭ по математике
- Демоверсия ОГЭ по информатике
- Демоверсия ОГЭ по математике
- Материалы по аттестации
- Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
- Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
- Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
- Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
- Тематическое планирование