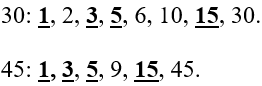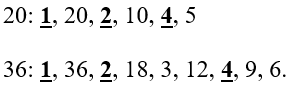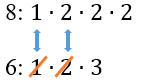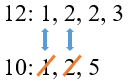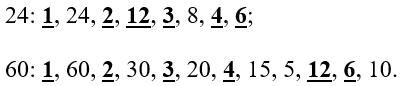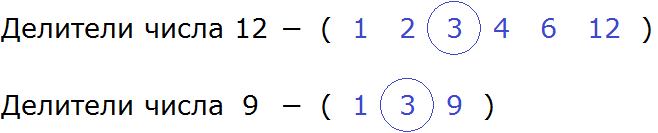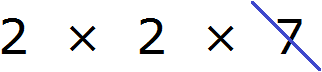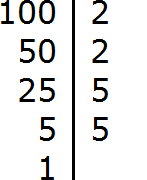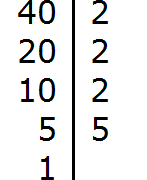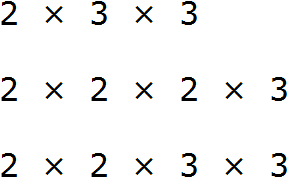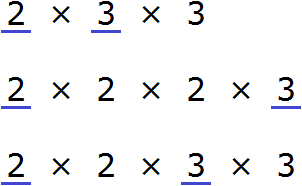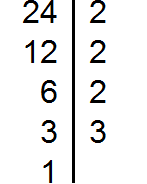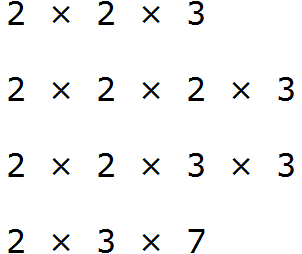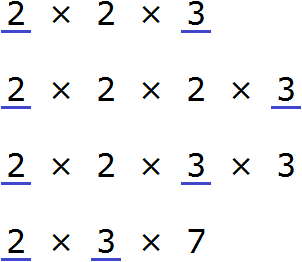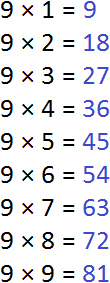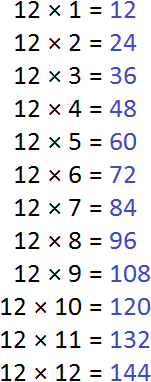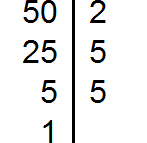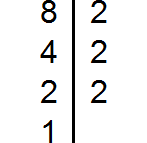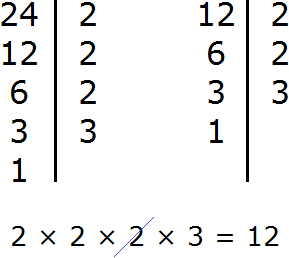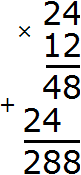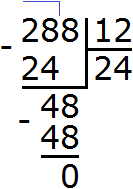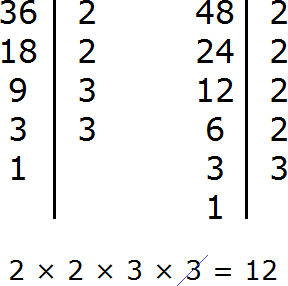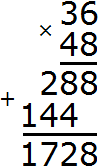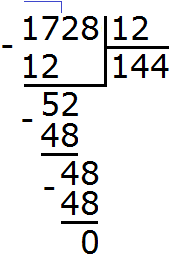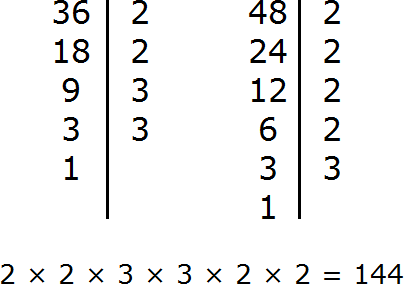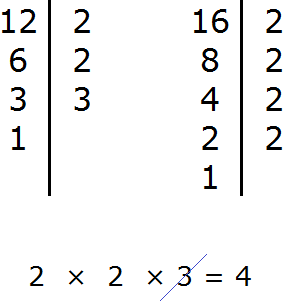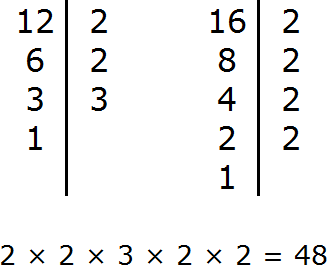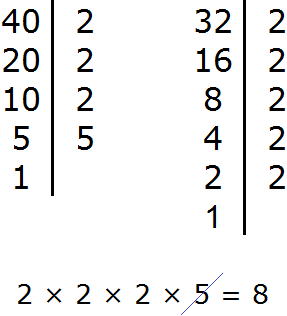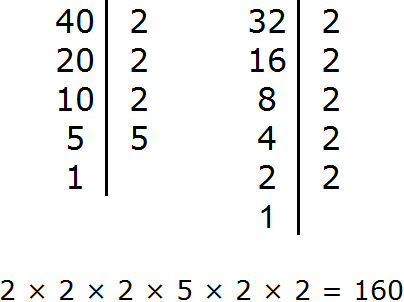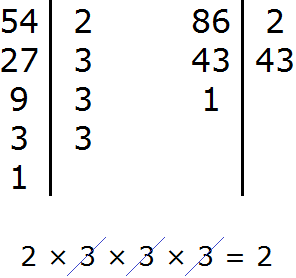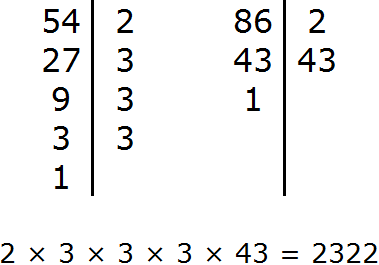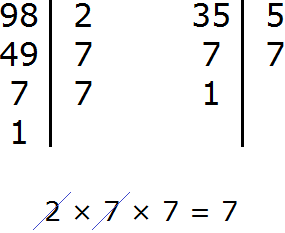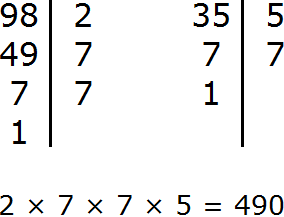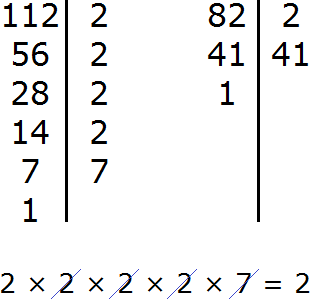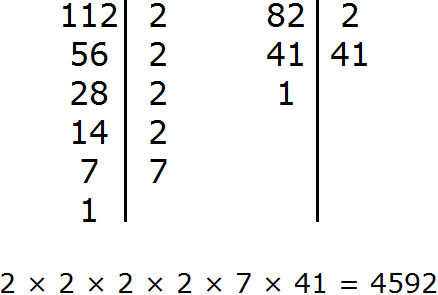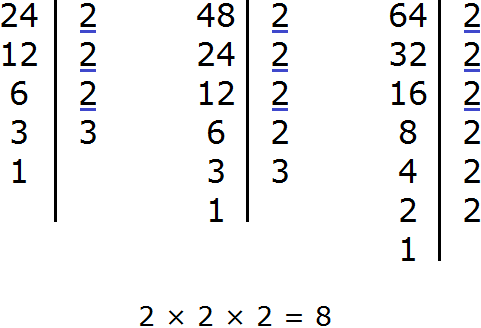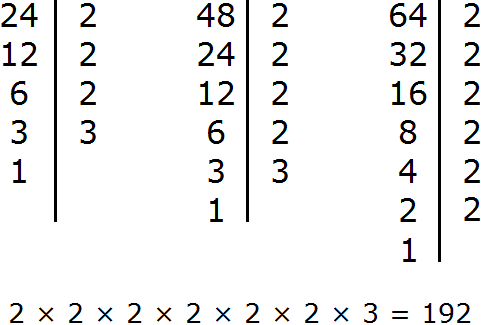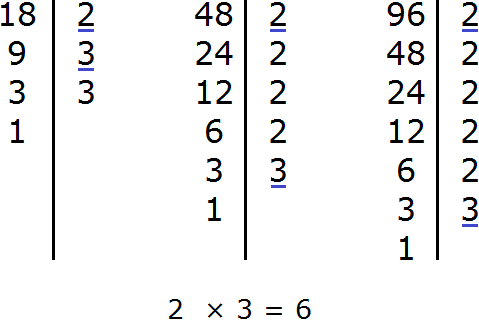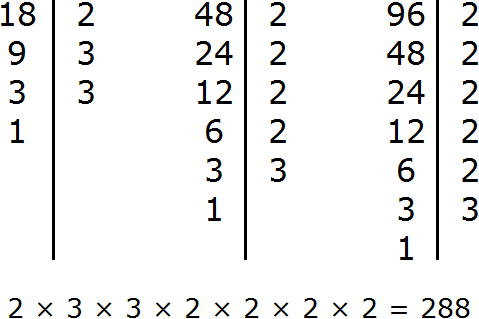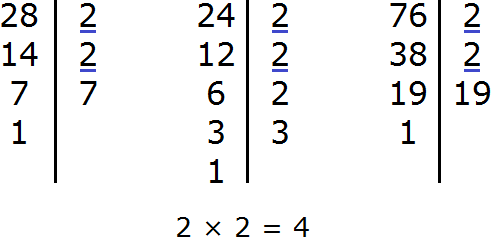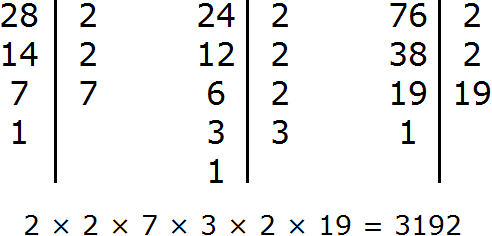Материалы этой главы ещё в разработке.
Подпишитесь на обновления, и мы сообщим, когда они будут доступны, — или расскажем о других новостях.
НОК и НОД
Рассмотрим выражение:
(45:9)
Можем сказать, что 45 – делимое, а 9 – делитель данного выражения.
Мы знаем, что 45 делится нацело на число 9. В таком случае, если мы захотим описать, чем эти числа являются друг другу, то мы скажем, что
9 – делитель числа 45
45 – кратно числу 9
Иногда при решении задач нужно находить общие кратные или общие делители двух чисел.
Наименьший делитель двух чисел – всегда единица. Такой делитель нет смысла искать, поэтому ищут наибольший общий делитель.
А кратных наоборот – бесконечно много, невозможно искать наибольшее из них, поэтому ищут, наименьшее общее кратное.
НОД:
Наибольший общий делитель (НОД) двух чисел – это наибольшее число, на которое каждое из этих чисел можно поделить без остатка.
Пример №1:
Рассмотрим числа 30 и 45.
-
Найдем все их существующие делители, т.е. числа, на которые каждое из них поделится нацело:
-
Мы видим, что у этих двух чисел есть несколько общих делителей. Наибольший из них – 15 – является самым большим. Это и есть НОД.
Значит и число 45 и число 30 можно нацело поделить на 15. Записывают это так:
(НОД (30;45) = 15)
Ответ: 15.
Пример №2:
Найдем (НОД (20;36):)
-
Выпишем все делители этих чисел.
Так же делители можно сразу записывать парой. Если 20 нацело делится на 2, то
(20 : 2 = 10)
Значит 10 – тоже делитель числа 20. Запишем делители 2 и 10 парой:
-
Выделим все общие делители и найдем наибольший из них. В данном случае
(НОД(20;35) = 4.)
Ответ: 4.
НОК:
Наименьшее общее кратное (НОК) двух чисел – это наименьшее число, которое можно поделить на каждое из этих чисел без остатка.
Пример №3:
Найдем (НОК (10;12).)
-
Возьмем наименьшее число. В данном случае – 10.
Будем умножать его на натуральные числа по порядку, пока не получим число, кратное 12, то есть такое, на которое нацело поделится и 10, и 12. Оно и будет НОК этих двух чисел. Такой метод называется методом подбора.
(10 bullet 1 = 10; 10 НЕ кратно 12)
(10 bullet 2 = 20; 20 НЕ кратно 12)
(10 bullet 3 = 30; 30 НЕ кратно 12)
(10 bullet 4 = 40; 40 НЕ кратно 12)
(10 bullet 5 = 50; 50 НЕ кратно 12)
(10 bullet 6 = 60; 60 кратно 12)
-
Первое число, которое будет кратно обоим числам и является их наименьшим общим кратным.
Общих кратный, в отличии от делителей, бесконечно много, поэтому обычно выбирают наименьший их них.
Ответ: 60.
Также можно находить НОК через разложение на множители:
Пример №4:
Найдём (НОК (6;8):)
-
Разложим числа 6 и 8 на простейшие множители, т.е. представим каждое число как произведения простых чисел. Множители большего числа запишем сверху:
8: (1 bullet 2 bullet 2 bullet 2)
6: (1 bullet 2 bullet 3)
-
Видим, что множители 1 и 2 повторяются у обоих чисел, поэтому для меньшего числа их уберем. Останется:
-
Перемножим все оставшиеся числа. Их произведение и будет НОК:
(НОК (6; 
Ответ: 24.
Пример №5:
Найдем (НОК (10;12)) разложением на множители:
-
Разложим оба числа на простые множители. Сверху запишем большее число:
12: 1, 2, 2, 3
10: 1, 2, 5
-
Для меньшего числа зачеркнем те множители, которые уже есть у большего числа:
-
Перемножим все оставшиеся числа:
(НОК (10; 12) = 1 bullet 2 bullet 2 bullet 3 bullet 5 = 60)
Наш ответ совпал с ответом, где мы использовали метод подбора.
Ответ: 60.
ВЗАИМОСВЯЗЬ НОК И НОД:
Произведение НОК и НОД некоторых чисел равно произведению самих этих чисел:
(НОК(a; b) bullet НОД(a; b) = a bullet b)
Докажем эту формулу на примере.
Пример №6:
Рассмотрим пару чисел 24 и 60.
-
Найдем их НОД:
(НОД (24;60) = 12)
-
Найдем их НОК:
(НОК (24; 60) = 1 bullet 2 bullet 2 bullet 2 bullet 3 bullet 5 = 120)
-
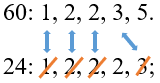
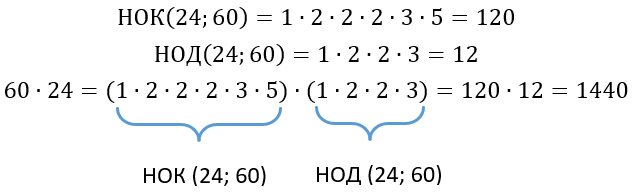
Рассмотрим поближе НОК. Чтобы его получить, мы переменожили все простые множители чисел 60 и 24 за исключением множителей 1, 2, 2, 3. Найдем отдельно их произведение:
(1 bullet 2 bullet 2 bullet 3 = 12)
Если перемножить все простые множители числе 60 и 24 мы получим просто их произведение, при этом оно будет состоять из НОК и числа 12, которое в свою очередь равно НОД:
План урока:
Наибольший общий делитель
Взаимно простые числа
Минутка истории
Наибольший общий делитель
Встречаются ситуации, когда хочется понимать, на какое максимальное количество делится одновременно несколько числовых значений.
Например:
В городском парке проводился ежегодный марафон. Для участия в марафоне пришло 36 мальчиков, 24 девочки. По условиям соревнования, всех участников необходимо поделить на команды, в которые войдут и мальчики, и девочки. Сколько одинаковых команд можно сформировать из данного количества детей?
Чтобы ответь на вопрос задачи, вычислим максимальное числовое значение, являющееся делителем для количества всех ребят одновременно.
Выполним необходимые вычисления – определим существующие множители. Вычисления запишем в столбик.
Начнем с 36.
36 | 2
18
Полученное частное – 18, оно четное. Делитель остается прежним:
36 | 2
18 | 2
9
9 – нечетное, поэтому берем следующий делитель – 3:
36 | 2
18 | 2
9 | 3
3
Частное – простое числовое значение, делится само на себя:
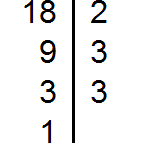
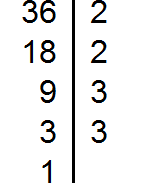
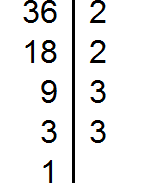
36 | 2
18 | 2
9 | 3
3 | 3
1
Частное – единица, разложение окончено.
Выпишем составляющие:
36 = 2×2×3×3
Переходим к 24.
24 заканчивается четной цифрой, значит, кратно двум:
242
12
Делитель оставляем прежним, частное 12 – четное:
242
122
6
Результат деления 6, снова делим на 2:
24 | 2
12 | 2
6 | 2
3
Получили простое числовое значение, которое делится само на себя:
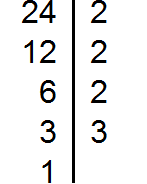
24 | 2
12 | 2
6 | 2
3 | 3
1
Разложение окончено. Запишем полученные компоненты:
24 = 2 × 2 × 2 × 3.
В финале выполненных вычислений мы получили:
36 = 2 × 2 × 2 × 3× 3;
24 = 2 × 2 × 2 × 3.
Давайте выберем одинаковые составляющие. Видно, что в каждом выражении такими составляющими будут: 2 ×2 × 3.
Перемножим выделенные компоненты:
2 ×2 × 3 = 12.
12 – самое большое числовое значение, на которое можно разделить оба делимых.
Мы выяснили, что всех участников можно распределить на 12 одинаковых команд.
Решая задачу, нашли самый большой делитель двух данных чисел. В арифметике число, являющееся самым большим делителем, одновременно для нескольких делимых, называют наибольшим общим делителем.
Для определения наибольшего общего делителя, нужно придерживаться определенного порядка выполнения математических действий:
Выполним задание.
Определите НОД (наибольший общий делитель) 66 и 44.
Чтобы выполнить задание будем придерживаться рассмотренного алгоритма действий.
Определим компоненты, входящие в состав числового значения.
Значит:
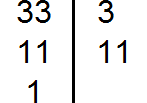
66 | 2
33
Результат деления оканчивается нечетной цифрой, проверяем по признакам делимости на 3:
66 | 2
33 | 3
11
Мы получили простое числовое значение
66 | 2
33 | 3
11 | 11
1
В итоге вычислений – 1, разложение окончено.
Переходим ко второму известному значению.
- 1) Определим составляющие, входящие в состав:
Проверяем по признакам делимости. Данное числовое значение заканчивается четной цифрой, значит, оно делится на 2.
44 | 2
22
Частное снова делится на 2:
44 | 2
22 | 2
11
В результате простое число, делим само на себя:
44 | 2
22 | 2
11 | 11
1
Разложение окончено.
- 2) Выпишем компоненты обоих делимых, определим одинаковые:
66 = 2 × 3 × 11
44 = 2 ×2 × 11
- 3) Перемножим выделенные составляющие:
2 × 11=22
Выходит, что наибольший общий делитель – 22.
На письме, рядом с обозначением НОД в скобочках записывают делимые, для которых определяли наибольший общий делитель:
НОД (66;44) = 22.
Разберем задачу
Выпускники на праздник последнего звонка, приготовили цветы своим учителям. Они принесли 69 роз и 46 гладиолусов и разделили поровну между всеми учителями. Сколько учителей поздравили выпускники?
Зная, что цветы были поделены поровну, нам необходимо найти максимальную численность учителей,на которую можно разделить и розы и гладиолусы.
Для определения НОД данных делимых, воспользуемся алгоритмом вычисления:
- 1) Разложим на составляющие:
69 | 3 46 | 2
23 | 23 23 | 23
1 1
- 2) Выберем общее числовое значение находящееся в составляющих :
69 = 3 × 23
46 = 2 × 23.
Нам подходит только 23.
НОД (69;46) = 23.
Наибольшим общим делителем для данных чисел будет 23.
Выпускники поздравили 23 учителя.
Взаимно простые числа
Рассмотрим ситуацию.
В первой банке лежало 9 декоративных камней, во второй – 14 . Сколько предметов интерьера, можно украсить имеющимся материалом, если на каждое изделие использовать равное, при этом, наибольшее количество,камней из первой и второй коробки?
Чтобы ответить на главный вопрос задачи, нужно выполнить определенные вычисления. Для этого, разложим данные значения на простые составляющие:
14 | 2 9 | 3
7 | 7 3 | 3
1 1
Выписываем компоненты, входящие в состав известных значений:
14 = 2 × 7
9 = 3 × 3
Повторяющихся составляющих нет. Мы знаем, если любое натуральное число умножить на 1, числовое значение не изменится. Значит, единственный, наибольший общий множитель чисел – 1.
Данным количеством камней получится украсить только один предмет интерьера, если использовать равное, наибольшее количество материала из обеих банок.
В арифметике числа, наибольшим общим множителем которых является 1, называют взаимно простыми.
Чтобы ответить на главный вопрос задачи, нужно выполнить определенные вычисления. Для этого, разложим данные значения на простые составляющие:
14 | 2 9 | 3
7 | 7 3 | 3
1 1
Выписываем компоненты, входящие в состав известных значений:
14 = 2 × 7
9 = 3 × 3
Повторяющихся составляющих нет. Мы знаем, если любое натуральное число умножить на 1, числовое значение не изменится. Значит, единственный, наибольший общий множитель чисел – 1.
Данным количеством камней, получится украсить только один предмет интерьера, если использовать равное, наибольшее количество материала из обеих банок.
В арифметике, числа, наибольшим общим множителем которых является 1, называют взаимно простыми
Чтобы ответить на главный вопрос задачи, необходимо определить самое маленькое числовое значение, которое будет, без остатка делиться на 4, на 5, то есть будет кратно 4, 5.
Сначала, подберем значения, кратные четырем: 4,8,12,16,20,24,28.
Теперь, значения, кратные пяти: 5,10,15,20,25,30.
После этого, необходимо найти самое маленькое число, которое будет кратным 4, 5 одновременно.
Из перечисленных числовых значений, подходит только 20. Оно делится без остатка на 4, на 5. Наименьшим общим кратным двух чисел будет 20.
Важно!
В математике существует специальный алгоритм для нахождения наименьшего общего кратного нескольких натуральных числовых значений:
Например:
Вычислим НОК для 30 и 32.
Чтобы выполнить нужные вычисления воспользуемся алгоритмом нахождения НОК.
Разберем задачу
В городе Москва, для качественной съемки парада, приуроченного к празднику 9 Мая, организаторы подготовили квадрокоптеры с видеокамерами. Из одной точки одновременно, будут запущены три аппарата. Время полета первого 8 минут, второго – 12.Через какое время,квадрокоптеры снова будут запущены одновременно, если по возвращению в точку запуска им меняют батарею и сразу отправляют назад.
Чтобы получить ответ на главный вопрос задачи, найдем наименьшее числовое значение, кратное двум данным величинам.
Для этого будем использовать рассмотренный алгоритм:
Квадрокоптеры будут одновременно запущены через 24 минуты.
Последняя задачка на внимательность.
На уроке Ваня около доски выполнял задание. Он написал: НОК (25; 115) = 100. Подскажите Ване, верно ли он выполнил задание (не выполняя вычислений)?
Вначале, давайте вспомним определение НОК:
Из определения следует, НОК нацело делится на известные данные. Однако,видим, что 100 на 115 нацело разделить невозможно. Поэтому Ваня, допустил ошибку в своих расчетах!
Вот так легко и просто можно решить огромное количество задач, даже не совершая сложных вычислений!
Пока, вы только ученики 6 класса. Пройдет совсем немного времени и каждому придется делать главный выбор в своей жизни – «Кем стать?». Если решите связать жизнь с программированием, интернет-ресурсами, научной деятельностью, вам нужно запомнить все правила и определения. Рассмотренные сегодня алгоритмы лежат в основе разработки, создания, компьютерных программ, сайтов, игр.
Минутка истории
1. Древнегреческий математик Эвклид, создавший алгоритм нахождения НОД, совершил множество математических открытий, аналогов которым ученые не нашли. Самым интересным, является то, что биографических сведений о самом Эвклиде не существует.
2. Среди бесконечного множества простых чисел, заканчивающихся на два и пять, существует только два: 2 и 5.
3. Результат суммирования цифр числа 18, в два раза меньше этого числа. Существует только одно число такого плана.
4. Однажды, математик Абрахам де Муавр, живший в Англии, находясь в преклонном возрасте, выяснил, что временной период, занимающий сон, увеличивается ежедневно на четвертую часть часа. Проведя вычисления, он определил день, когда длительность сна достигнет суток. По его расчетам это должно произойти двадцать седьмого ноября 1754 года. Именно эта дата стала датой смерти английского ученого.
Нахождение НОК и НОД двух натуральных чисел
Содержание:
- Что такое НОК и НОД двух натуральных чисел
- Особенности вычисления, алгоритм Евклида
- Правило нахождения наибольшего общего делителя (НОД)
- Правило нахождения наименьшего общего кратного (НОК)
Что такое НОК и НОД двух натуральных чисел
Натуральными числами называют числа, которые используются при счете – 1, 2, 3, 16, 25, 101, 2560 и далее до бесконечности. Ноль, отрицательные и дробные или нецелые числа не относятся к натуральным.
Наименьшее общее кратное (НОК) двух натуральных чисел a и b – это наименьшее число, которое делится без остатка на каждое из рассматриваемых чисел.
Наибольший общий делитель (НОД) двух натуральных чисел a и b – это наибольшее число, на которое делится без остатка каждое рассматриваемое число.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свойства НОК и НОД для натуральных чисел a и b
- (НОД (a, b) = НОД (b, a);)
- (НОК (a, b) = НОК (b, a);)
- (НОК;(a,b)=frac{a;times;b}{НОД;(a,b)}.)
Особенности вычисления, алгоритм Евклида
Рассмотрим два способа определения НОД и НОК с помощью алгоритма Евклида:
- Способ деления.
При делении целых чисел с остатком, где a — делимое, b – делитель (b не равно 0) находят целые числа q и r согласно равенству (a=btimes) q+r, в котором q – неполное частное, r – остаток при делении (не отрицательное, по модулю меньше делителя).
Чтобы вычислить НОД, первоначально нужно выбрать наибольшее из двух чисел и поделить его на меньшее. Пока остаток не станет равным нулю, повторяется цикл деления делителя на остаток от деления в соответствии с формулой.
Пример №1
Вычислим НОД для чисел 12 и 20. Делим 20 на 12 и получаем 1 и 8 в остатке. Запишем иначе:
(20=12times1+8), так как остаток не равняется нулю, продолжаем деление. Делим 12 на 8 и получаем 1 и 4 в остатке. Записываем: (12=8times1+4) и по аналогии делим 8 на 4 и получаем 2 и 0 в остатке. НОД равен остатку, предшествующему нулю.
НОД (12;20) = 4
НОК получаем согласно свойству (НОК (a, b) = НОК;(a,b)=frac{a;times;b}{НОД;(a,b)}.) Подставляем числовые значения:
НОК (12; 20) = (12times20div4=60)
НОК (12;20) = 60
- Способ вычитания.
Здесь повторяется цикл вычитания из наибольшего числа меньшего числа до момента, пока разность не станет равна нулю. НОД равен предшествующей нулю разности.
Пример №2
Вычислим НОД для тех же чисел, 12 и 20.
20 – 12 = 8 (разность не равна нулю, продолжаем)
12 – 8 = 4
8 – 4 = 4
4 – 4 = 0
НОД (12;20) = 4
НОК находим также, как и при методе деления.
Правило нахождения наибольшего общего делителя (НОД)
Для нахождения наибольшего общего делителя воспользуемся пошаговым алгоритмом:
- Разложить числа на простые множители.
- Найти общий множитель одного и другого числа.
- Перемножить общие множители, если их несколько, и их произведение будет НОД.
Пример №3
Возьмем натуральные числа 24 и 36.
(24=2times2times2times3)
(36=2times2times3times3)
Правильно записать следующим образом:
(НОД (24;36)=2times3=6)
Примечание
В случае, когда одно или оба числа относятся к простым, т.е. делятся только на единицу и на само себя, то их НОД равняется 1.
Правило нахождения наименьшего общего кратного (НОК)
Для нахождения наименьшего общего кратного воспользуемся подробным алгоритмом:
- Наибольшее из чисел, а затем остальные разложить на простые множители.
- Выделить те множители, которые отсутствуют у наибольшего.
- Перемножить множители п. 2 и множители наибольшего числа, получить НОК.
Пример №4
Возьмем натуральные числа 9 и 12.
(12=2times2times3)
(9=3times3) (видим, что у числа 12 отсутствует одна тройка)
Правильно записать следующим образом:
(НОК (9;12)=2times2times3times3=36)
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: и
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
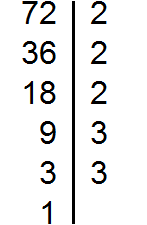
Раскладываем на множители число 72
Раскладываем на множители число 128
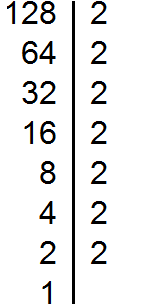
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
Разложим на множители число 36
Разложим на множители число 42
Получили четыре разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
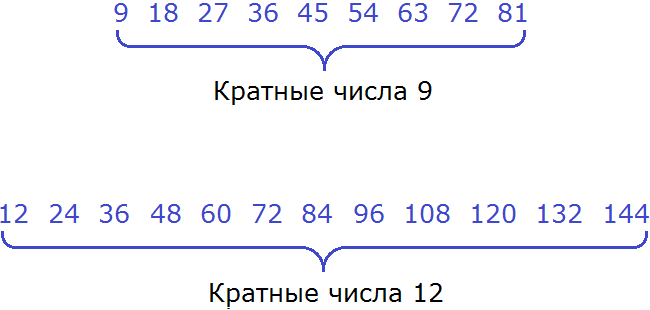
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
Теперь выпишем кратные обоих чисел:
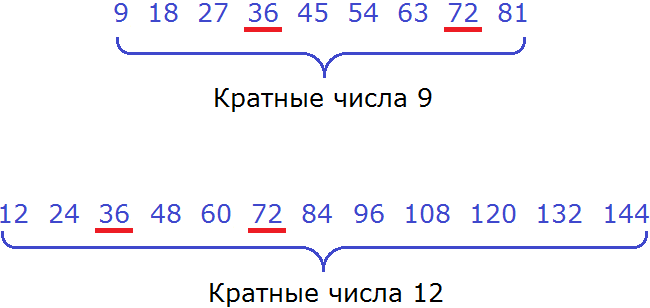
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
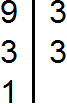
Разложим на множители число 9
Разложим на множители число 12
Выпишем первое разложение:
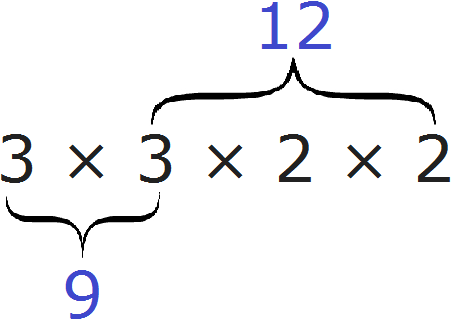
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
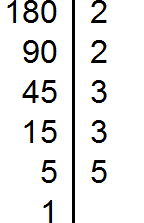
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
Разложим на множители число 180
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
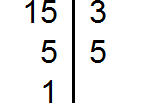
Пример 3. Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
Разложим на множители число 15
Разложим на множители число 33
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
Разделим полученное число 288 на НОД чисел 24 и 12
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
Перемножим числа 36 и 48
Разделим 1728 на НОД чисел 36 и 48
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Задание 1. Найдите НОД чисел 12 и 16
Решение:
Задание 2. Найдите НОК чисел 12 и 16
Решение:
Задание 3. Найдите НОД чисел 40 и 32
Решение:
Задание 4. Найдите НОК чисел 40 и 32
Решение:
Задание 5. Найдите НОД чисел 54 и 86
Решение:
Задание 6. Найдите НОК чисел 54 и 86
Решение:
Задание 7. Найдите НОД чисел 98 и 35
Решение:
Задание 8. Найдите НОК чисел 98 и 35
Решение:
Задание 9. Найдите НОД чисел 112 и 82
Решение:
Задание 10. Найдите НОК чисел 112 и 82
Решение:
Задание 11. Найдите НОД чисел 24, 48, 64
Решение:
Задание 12. Найдите НОК чисел 24, 48, 64
Решение:
Задание 13. Найдите НОД чисел 18, 48, 96
Решение:
Задание 14. Найдите НОК чисел 18, 48, 96
Решение:
Задание 15. Найдите НОД чисел 28, 24, 76
Решение:
Задание 16. Найдите НОК чисел 28, 24, 76
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже