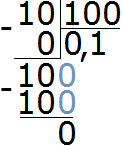Формула
Чтобы вычислить, на сколько процентов одно число меньше другого, нужно из 100 вычесть отношение первого числа ко второму, умноженное на 100.
Р = 100 − Ч1Ч2 · 100
Таким же образом можно определить на сколько процентов уменьшилось число. Например, размер ваших накоплений, после того, как часть была потрачена на отпуск.
Примеры
Вычислим, на сколько процентов число 5 меньше числа 20:
100 − 520 · 100 = 100 − 0,25 · 100 = 100 − 25 = 75%
Число 5 меньше числа 20 на 75%.
Например, фрилансер Олег в январе выполнил заказы на 40000 рублей, а в феврале на 30000 рублей. Найдем, на сколько процентов Олег в феврале заработал меньше, чем в январе:
100 − 3000040000 · 100 = 100 − 0,75 * 100 = 100 − 75 = 25%
Таким образом, в феврале Олег заработал на 25% меньше, чем в январе.
Вычисление числа на заданный процент большего или меньшего от исходного числа
Формула вычисления числа, которое больше исходного числа на заданный процент.
Если дано число A и необходимо найти число B, которое на P процентов больше числа A, то
Формула вычисления числа, которое меньше исходного числа на заданный процент.
Если дано число A и необходимо найти число B, которое на P процентов меньше числа A, то
Вывод формул:
-
найти P процентов от числа A
-
добавить полученное число к числу A, если ищется число, которое больше исходного:
A + A · P = A(1 + P ) 100% 100% вычесть полученное число из числу A, если ищется число, которое меньше исходного:
A — A · P = A(1 — P ) 100% 100%
Примеры решения задач о вычисление числа на заданный процент большего или меньшего от исходного числа
Пример 1.
Найти число, которое на 5% больше 40.
Решение:
Ответ: число 42 на 5% больше чем 40.
Пример 2.
Найти число, которое на 5% меньше 40.
Решение:
Ответ: число 38 на 5% меньше 40.
Пример 3.
Какая сумма будет через год на счету в банке если положить на депозит 1000 рублей под 10% годовых.
Решение:
| 1000 · (1 + | 10% | ) = 1100 |
| 100% |
Ответ: на депозите будет 1100 рублей.
При изучении процентов вам также будут полезны:
Чтобы узнать, на сколько процентов одно число больше или меньше другого, очень удобно воспользоваться следующими формулами:
Формула 1
если высчитывать, на сколько число больше другого, нужно
Формула 2
если высчитывать, на сколько число меньше другого, нужно
В обеих случаях выполняем примерно одинаковые действия и здесь нужно быть очень внимательным, чтобы ничего не напутать.
Почему нужно быть внимательным? — Потому что если сравнивать два два числа по разному — получим разные результаты.
Проверим это на примерах, которые уже есть в ответах на этот вопрос:
сравним числа 160 и 80
из первой формулы узнаем, что число 160 больше числа 80 на 100%
р%=(160-80)/80*100%=100%
из второй формулы узнаем, что число 80 меньше числа 160 на 50%
р%=(160-80)/160*100%=50%.
Аналогично узнаем, что число 20 больше числа 15 на 33,33%, а число 15 меньше числа 20 на 25%.
Если сравнивать числа, которые своими номиналами будут не очень сильно отличаться друг от друга (например числа 100 и 101) тогда процентная разница будет незаметна, но она все равно будет
101 больше 100 на 1% а число 100 меньше 101 на 0,99%
На сколько процентов меньше
Рассчитайте онлайн, на сколько процентов одно число меньше другого.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что считает калькулятор?
Калькулятор предназначен для расчета на сколько процентов одно число меньше другого. Это полезный инструмент в различных сферах, таких как финансы, бизнес и личные финансы. Калькуляторы процентов могут использоваться для расчета процентов по кредитам, депозитам, инвестициям, а также для налоговых расчетов и других задач. Они могут помочь быстро и точно выполнить расчеты, которые могут быть сложными при выполнении вручную, что позволяет сэкономить время и уменьшить вероятность ошибок.
Как считать на калькуляторе процентов
Калькулятор операций с процентами предназначен для упрощения расчетов с процентами. Для его использования, вам необходимо выбрать ввести число и значение процентов. Например, если вы хотите вычислить на сколько процентов число 20 меньше числа 5, введите числа 20 и 5 в соответствующие поля, а также укажите степень округления после запятой. После этого калькулятор выдаст вам ответ, который составляет -300%.
Где можно применить калькулятор процентов
Калькулятор операций с процентами может быть полезен во многих ситуациях, где необходимо производить расчеты, связанные с процентами. Некоторые из областей, где калькулятор с процентами может быть использован, включают:
- 🪙 Финансы. Расчет процентов по кредитам, ипотеке, вкладам, облигациям, инвестициям, налогам и т.д.
- 🥼 Медицина. Расчет процентов смертности, выживаемости, процентов телесной жировой массы и т.д.
- 👩🏻💼 Бизнес. Расчет налоговых вычетов, налоговой базы, налоговых скидок, общей суммы платежа за товары и услуги, расчет маржинальности и т.д.
- 👩🏫 Образование. Расчет оценок, процентов скидок на учебники, процентов успешных сдач экзаменов и т.д.
- 🧾 Персональные финансы. Расчет бюджета, расходов на различные категории, процентов от заработной платы, калькуляторы кредитных карт и т.д.
Калькулятор процентов также может быть полезен для обучения математике, включая процентные расчеты, а также для использования в повседневной жизни для быстрых расчетов.
Как самостоятельно вычислить на сколько процентов одно число меньше другого числа
Чтобы вычислить на сколько процентов одно число меньше другого числа, можно использовать следующую формулу:
((Старшее число — Младшее число) / Старшее число) * 100
Где «Старшее число» — это число, которое больше, а «Младшее число» — это число, которое меньше.
Например, пусть у нас есть числа 50 и 70, и мы хотим вычислить, на сколько процентов 50 меньше, чем 70. Тогда мы можем использовать формулу:
((70 — 50) / 70) * 100 = 28.57%
Значит, число 50 меньше на 28.57% по сравнению с числом 70.
Полезные советы
Вот несколько советов, которые могут помочь при расчете процентов:
- Освойте основные формулы для расчета процентов, такие как формулы для нахождения процентного соотношения, процентного приращения или процентного уменьшения.
- Помните, что проценты могут быть выражены как десятичные дроби, например, 50% может быть записано как 0.5.
- Не забывайте учитывать порядок операций, например, в выражении «25% от 80» сначала нужно умножить 80 на 0,25, а затем округлить результат.
- Используйте дроби для более точных расчетов, особенно если нужно произвести несколько операций. Например, вы можете записать «25% от 80» как 1/4 от 80.
- Учитывайте различные типы процентов, например, простые и сложные проценты. Для расчета сложных процентов вам может потребоваться использовать формулу с учетом периода начисления процентов.
- Используйте калькулятор при необходимости, особенно при более сложных расчетах. Это может помочь избежать ошибок при пересчете значений.
- Не забывайте проверять свои расчеты на ошибки и перепроверять полученные результаты, чтобы убедиться в их правильности.
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемые вопросы при вычислении процентов.
Как вычислить процент от числа?
Для вычисления процента от числа нужно умножить число на процентное соотношение (долю) в виде десятичной дроби. Например, чтобы найти 25% от числа 200, нужно выполнить следующее вычисление: 200 x 0,25 = 50.
Как вычислить число, которому соответствует определенный процент?
Чтобы найти число, соответствующее определенному проценту, нужно разделить процентное значение на процентное соотношение (долю) в виде десятичной дроби. Например, чтобы найти число, которому соответствует 20%, нужно выполнить следующее вычисление: 20 ÷ 100 x N = N x 0,2.
Как вычислить процент изменения?
Чтобы вычислить процент изменения, нужно найти разницу между начальным и конечным значениями, разделить ее на начальное значение и умножить на 100%. Например, если начальное значение равно 100, а конечное значение равно 120, то процент изменения будет: ((120-100) ÷ 100) x 100% = 20%.
Как вычислить начальное значение при известном конечном значении и процентном изменении?
Чтобы найти начальное значение при известном конечном значении и процентном изменении, нужно разделить конечное значение на 1 плюс процент изменения в виде десятичной дроби. Например, если конечное значение равно 120, а процент изменения равен 20%, то начальное значение будет: 120 ÷ (1 + 0,2) = 100.
Как вычислить конечное значение при известном начальном значении и процентном изменении?
Чтобы найти конечное значение при известном начальном значении и процентном изменении, нужно умножить начальное значение на 1 плюс процент изменения в виде десятичной дроби. Например, если начальное значение равно 100, а процент изменения равен 20%, то конечное значение будет: 100 x (1 + 0,2) = 120.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор логарифмов. Вычислите онлайн натуральные, десятичные логарифмы (или с другим основанием) с решением.
- Возведение дроби в степень. Возведите онлайн любую дробь (десятичную и обыкноенную) в любую степень.
- Калькулятор процентов от числа. Рассчитайте онлайн значение процента от любого числа с помощью данного калькулятора.
- Калькулятор процентов. Рассчитайте онлайн процент от числа, на сколько процентов одно число больше или меньше другого, или сколько процентов составляет одно число от другого числа, а также прибавьте или вычтете процент к числу.
- Добавить процент к числу. Прибавьте онлайн любой процент к любому числу с помощью специального калькулятора.
- Вычесть процент из числа. Вычтете онлайн любой процент от любого числа с помощью специального калькулятора.
- На сколько процентов больше. Рассчитайте онлайн, на сколько процентов одно число больше другого.
- Тренажер таблицы умножения. Тренируйтесь и запоминайте таблицу умножения онлайн. Выберите нужный диапазон множителей, и система сгенерирует задания.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Содержание
- Проценты
- Что такое процент?
- Как найти процент?
- Второй способ нахождения процента
- Нахождения числа по его проценту
- Как найти число по его проценту?
- Конспект по математике «Решения задач на проценты»
- Наиболее распространенные типы задач на проценты
- Видео
- Нахождение числа по его процентам
- Второй способ нахождения процента
- Решение задач на проценты с помощью формулы простого процента
- Как найти процентное соотношение чисел
- Проценты и десятичные дроби
- Что такое процент?
- Онлайн-сервисы для вычислений
- Формулы для решения задач на проценты
- Перевод процентов в десятичную дробь
Проценты
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.
Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.
Процентом является одна сотая часть
Например, 
от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:
Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
1% = = 0,01
Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:
Значит 2% от 10 см составляют 2 мм.
Пример 2. Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей на 100
Теперь полученный результат умножаем на 50
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти 
от 300 рублей, а решать такие задачи для нас пока проще
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.
Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
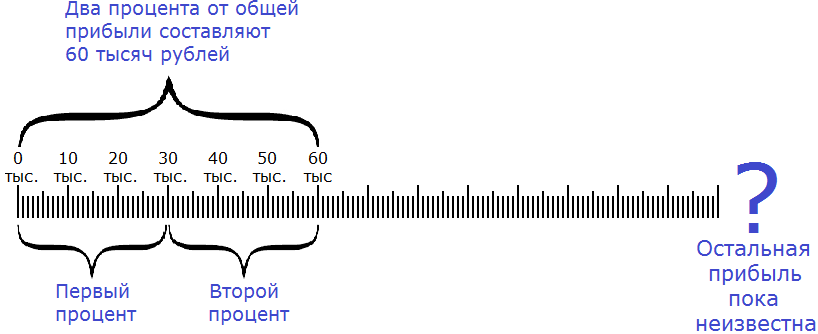
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000 : 2 = 30 000
Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это 
от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Источник
Как найти число по его проценту?
Как найти число, если известен его процент?
Давайте разбираться.
Задание 1.
Надо найти число, если известно, что 23% — это 138.
Решение:
1). Сначала найдем чему равен 1%.
Нам известно, что 23% это 138, значит, чтобы найти 1%, надо — 138 : 23 = 6.
Т.е. 1% — это 6.
2). Теперь надо найти целое число.
Мы знаем, что в целом – 100%.
А, чтобы найти целое, надо 1% умножить на 100.
Т.е. 6 х 100 = 600.
Значит, 100% — это 600 и это – целое число.
Ответ: 600.
Задание 2.
Найти число, если 12% — это 48.
Решение:
1). Превратим 12 % в десятичную дробь.
Если 1% = 1/100, то 12% =12/100
2). 12/100 – это 48,
Найдем 1/100, для этого 48 разделим на 12 и умножим на 100, 48 : 12 х 100.
Заменим знак «:» дробной чертой, будет 48/12 х 100, или по правилу работы с дробями – 48 х 100/12.
Получается — 48 : 12 х 100 = 48/12 х 100 = 48х100/12 = 48 х 100/12.
Таким образом, видно, что часть мы умножаем на обратную дробь или делим на дробь.
Т.е. 48 х 100/12 = 4800/12 = 400
Ответ: 400.
При решении примеров надо выбирать удобный для вас вариант.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 73
Источник
Конспект по математике «Решения задач на проценты»
Наиболее распространенные типы задач на проценты
- Найти указанный процент от заданного числа.
- Найти число по заданному другому числу и его величине в процентах от искомого числа.
- Найти процентное выражение одного числа от другого.
- Найти число на заданный процент большее (меньшее) исходного числа.
- Найти число, зная значение числа большего (меньшего) от исходного на заданный процент.
- Найти сложные проценты.
Видео
Нахождение числа по его процентам
Чтобы найти число по данной величине его процентов, нужно эту величину разделить на число процентов и умножить на 100.
Задача. Цена метра сукна снизилась на 24 руб., что составило 15% цены. Сколько стоил метр сукна до снижения?
Ответ: Метр сукна стоил 160 рублей.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись 
, а если перевести эти 
в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Решение задач на проценты с помощью формулы простого процента
Формула, которой мы пользуемся при решении задач на проценты, называется формула простого процента:
Хконечное – конечная величина
Хпервоначальное – первоначальная величина
k – процент, на который первоначальная величина изменилась
Из этой формулы всегда можно найти первоначальную величину или процент, на который происходит изменение.
Знак стоящий перед k зависит от того, увеличивается первоначальная величина или уменьшается. Так, если величина увеличивается на сколько-то процентов, то ставим знак плюс. Если уменьшается – минус.
Для наглядности приведем несколько простых примеров.
Как найти процентное соотношение чисел
Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.
Для определения такого результата существуют следующая формула:
К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.
Используя приведённую формулу, выполняем несложные арифметические операции:
85 / 500 * 100 = 17%
Таким образом, число 85 составляет 17% от 500.
Проверяем полученное число по формуле первого способа:
500 / 100 * 17 = 85.
Проценты и десятичные дроби
В разобранных выше примерах мы убедились, что вместо знака процента % можно писать ( displaystyle frac<1><100>), или просто разделить на ( displaystyle 100). То есть, ( displaystyle 25%) – это то же самое, что ( displaystyle frac<25><100>); ( displaystyle 247%) – это ( displaystyle frac<247><100>) и так далее. Но ведь любую из этих дробей можно записать компактнее: в виде десятичной дроби.
Например:
Значит, проценты можно записать в виде десятичной дроби.
Правило перевода такое: сколько бы ни было процентов, смещаем десятичную запятую на два знака влево и убираем значок % – и таким образом получаем обычное число. Данное правило будем теперь всегда применять сразу.
Например:
1. Чему равны ( displaystyle 35%) от числа ( displaystyle 60)?
Вместо ( displaystyle 35%) напишем что? ( displaystyle 0,35). Итак, ( displaystyle 0,35cdot 60=21).
2. ( displaystyle 48%) от какого числа равны ( displaystyle 456)?
( displaystyle 0,48x=456text< >Rightarrow text< >x=frac<456><0,48>=950).
Что такое процент?
Самое очевидное определение: процент – это десятичная дробь. В жизни редко что-то можно сравнивать целиком, чаще приходится сравнивать разные части чего-то целого. Поэтому мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Ну да, все так привыкли к слову «четверть» в школе, что забывают о его формальном значении – «четвертая часть учебного года». Сравнивать сотые доли удобнее всего – так появился процент (1/100): pro centum – «за сто» на латыни.
Все задачи по математике на проценты вертятся вокруг сравнения частей одного целого, определения, какую долю составляет часть от целого, нахождения целого исходя из величины его части и т.п.
Проценты можно записать со знакомым всем значком процента: 1%. Можно представить в виде десятичной дроби (или натурального числа). Для этого нужно разделить на 100: 0,01. Можно наоборот: выразить число в процентах. Тогда его следует умножить на 100%.
Онлайн-сервисы для вычислений
В нахождении нужных процентов могут помочь различные сервисы-калькуляторы, работающие в режиме онлайн. Например, популярный сайт имеет в своём функционале различные инструменты, помогающие, в том числе, высчитать процент от любого числа.
- Перейдите на .
- Введите искомые показатели в соответствующие клетки.
- Нажмите на «Рассчитать». Вы сразу же получите искомый результат.
Также указанный калькулятор позволяет высчитать какую долю от 1 составляет 2, прибавить % к числу или вычесть из него. Всё очень быстро и удобно.
Формулы для решения задач на проценты
- Формула вычисления процента от заданного числа. Если дано число A и необходимо вычислить число B, составляющее P процентов от A, то
- Формула вычисления числа по его проценту. Если дано число B которое составляет P процентов от числа A и необходимо найти значение числа A, то
- Формула вычисления процентного выражение одного числа от другого. Если дано два числа A и B и необходимо определить, какой процент составляет число B от числа A, то
- Формула вычисления числа, которое больше исходного числа на заданный процент. Если дано число A и необходимо найти число B, которое на P процентов больше числа A, то
- Формула вычисления числа, которое меньше исходного числа на заданный процент. Если дано число A и необходимо найти число B, которое на P процентов меньше числа A, то
- Формула вычисления исходного числа по значению числа, которое больше от исходного на заданный процент. Если дано число B, которое на P процентов больше числа A и необходимо найти число A, то
- Формула вычисления исходного числа по значению числа, которое меньше от исходного на заданный процент. Если дано число B, которое на P процентов меньше числа A и необходимо найти число A, то
- Формула вычисления сложных процентов.
где B — будущая стоимость; A — текущая стоимость; P — процентная ставка за расчетный период (день, месяц, год, …); n — количество расчетных периодов.
Перевод процентов в десятичную дробь
Чтобы перевести проценты в десятичную дробь, надо количество процентов разделить на 100.
Пример 1. Представить 25% в виде десятичной дроби.
Ответ: 25% — это 0,25.
Пример 2. Выразить 100% десятичной дробью.
Ответ: 100% — это 1.
Пример 3. Выразить 230% десятичной дробью.
Ответ: 230% — это 2,3.
Из данных примеров следует, что для перевода процентов в десятичные дроби, надо в числе, стоящем перед знаком % , перенести запятую на два знака влево.
Источник