Как найти наилучшую оценку результатов измерения

Задачей
измерения является нахождение по
полученным наблюдениям наилучшей
оценки измеряемой величины 
результата
измерения
и оценки точности этого результата,
т.е. степени его близости к истинному
значению величины 
погрешности
измерений.
При этом считается, что закон распределения
наблюдений и погрешностей известен.
Под оценкой
в данном случае понимается нахождение
значений параметров этих распределений
случайных величин по ограниченному
числу наблюдений. Полученные оценки
параметров распределений являются лишь
приближениями к истинным значениям
этих параметров и используются в качестве
результата измерений и его погрешности.
Для того чтобы оценку, получаемую по
результатам многократных наблюдений,
можно было использовать в качестве
параметра функции распределения
случайной величины, она должна отвечать
ряду требований — быть состоятельной,
несмещенной и эффективной.

Состоятельная
оценка – это
оценка, которая при увеличении числа
наблюдений стремится к истинному
значению оцениваемого параметра.

Несмещенная
оценка —
оценка, математическое ожидание которой
равно истинному значению оцениваемого
параметра.

Эффективная
оценка –
оценка, имеющая наименьшую дисперсию
по сравнению с любой другой оценкой
данного параметра.

Методы
нахождения оценок параметров распределений,
а по ним результатов измерений и их
погрешностей зависят от вида функции
распределения и от тех соглашений
по обработке результатов измерений,
которые нормируются в рамках законодательной
метрологии в нормативной документации.

4.5.4 Примеры распределения случайных величин

Способы
нахождения значений случайной величины
зависят от вида функции ее распределения.
Однако на практике такие функции, как
правило, неизвестны. Если же случайный
характер результатов наблюдений
обусловлен погрешностями измерений,
то полагают, что наблюдения имеют
нормальное
распределение.
Это обусловлено тем, что погрешности
измерений складываются из большого
числа небольших возмущений, ни одно из
которых не является преобладающим.
Согласно же центральной
предельной теореме
сумма бесконечно большого числа взаимно
независимых бесконечно малых случайных
величин с любыми распределениями имеет
нормальное
распределение.
Нормальное распределение для случайной
величиных
с математическим
ожиданием

и диспер-сией

имеет вид:

Реально даже
воздействие ограниченного числа
возмущений приводит к нормальному
распределению результатов измерений
и их погрешностей. В настоящее время
наиболее полно разработан математический
аппарат именно для случайных величин,
имеющих нормальное распределение. Если
же предположение о нормальности
распределения отвергается, то
статистическая обработка наблюдений
существенно усложняется и в таком случае
невозможно рекомендовать общую методику
статистической обработки наблюдений.
Часто даже не известно, какая характеристика
распределения может служить оценкой
истинного значения измеряемой величины.

Выше
приведено аналитическое выражение
нормального распределения для случайной
измеряемой величины х.
Переход к нормальному
распределению случайных погрешностей
осуществляется
переносом центра распределений ви откладывания по оси абсцисс погрешности
.

Нормальное
распределение характеризуется двумя
парамет-рами: математическим ожиданием
m₁
и
средним квадратическим отклонением σ.

При
многократных измерениях несмещенной,
состоятельной и эффективной оценкой
m₁
для группы из n
наблюдений является среднее арифметическое
:

.

Нужно
сказать, что среднее арифметическое
дает оценку математического ожидания
результата наблюдений и может быть
оценкой
истинного (действительного) значения
измеряемой
величины только после
исключения
систематических погрешностей.

Оценка
S
среднего квадратического отклонения
(СКО) дается формулой:

Эта
оценка характеризует рассеяние
единичных результатов измерений в ряду
равноточных измерений одной и той же
величины около их среднего значения.

Другими
оценками рассеяния результатов в ряду
измерений являются размах
(разница между наибольшим и наименьшим
значением), модуль средней
арифметической погрешности
(арифметическая сумма погрешностей,
деленная на число измерений) и доверительная
граница погрешности (подробно
рассматривается ниже).

СКО является
наиболее удобной характеристикой
погрешности в случае ее дальнейшего
преобразования. Например, для нескольких
некоррелированных слагаемых СКО суммы
определяется по формуле:

.

Оценка
S
характеризует рассеяние единичных
результатов наблюдений относительно
среднего значения, то есть в случае,
если мы за результат измерений примем
отдельный исправленный результат
наблюдений. Если же в качестве результата
измерений принимается среднее
арифметическое, то СКО этого среднего
определяется
по формуле:

Нормальное
распределение погрешностей имеет
следующие свойства:

1. симметричность,
   т.е. погрешности, одинаковые по величине,
   но противоположные по знаку, встречаются
   одинаково часто;

2. математическое
   ожидание случайной погрешности равно
   нулю;

3. малые
   погрешности более вероятны, чем большие;

4. чем
   меньше ,
   тем меньше рассеяние результатов
   наблюдений и больше вероятность малых
   погрешностей.

Другим
распространенным в метрологии
распределением случайной величины
является равномерное
распределение

распределение, при котором случайная
величина принимает значения в пределах
конечного интервала от х₁
до х₂
с постоянной плотностью вероятностей.

Дифференциальная
функция равномерного распределения
имеет вид:

f(x)
= с при
х₁

x

х₂

f(x)
= 0 при
х₂

x

х₁

При
нормировке площади кривой распределения
на единицу, получаем, что с(х₂
– х₁)
= 1 и с = 1/ (х₂
– х₁).

Равномерное
распределение характеризуется
математичес-ким ожиданием,
дисперсиейили СКО_.

Кроме
рассмотренных примеров распределений
случайных величин существуют и другие
важные для практического использования
распределения дискретных случайных
величин, например, биномиальное
распределение и распределение Пуассона.
В настоящем курсе они не рассматриваются.

Характеристики оценки измеряемой величины

Задачей измерения является нахождение по полученным наблюдениям наилучшей оценки измеряемой величины — результата измерения и оценки точности этого результата, т.е. степени его близости к истинному значению величины — погрешности измерений. При этом считается, что закон распределения наблюдений и погрешностей известен. Под оценкой в данном случае понимается нахождение значений параметров этих распределений случайных величин по ограниченному числу наблюдений. Полученные оценки параметров распределений являются лишь приближениями к истинным значениям этих параметров и используются в качестве результата измерений и его погрешности. Для того чтобы оценку, получаемую по результатам многократных наблюдений, можно было использовать в качестве параметра функции распределения случайной величины, она должна отвечать ряду требований — быть состоятельной, несмещенной и эффективной.

Состоятельная оценка – это оценка, которая при увеличении числа наблюдений стремится к истинному значению оцениваемого параметра.

Несмещенная оценка — оценка, математическое ожидание которой равно истинному значению оцениваемого параметра.

Эффективная оценка – оценка, имеющая наименьшую дисперсию по сравнению с любой другой оценкой данного параметра.

Методы нахождения оценок параметров распределений, а по ним результатов измерений и их погрешностей зависят от вида функции распределения и от тех соглашений по обработке результатов измерений, которые нормируются в рамках законодательной метрологии в нормативной документации.

Источник

Оценка измеряемой величины и среднее квадратическое отклонение

Кафедра «Мехатронные системы»

П.В. Лекомцев

Методические указания к лабораторной работе № 1

«Обработка результатов электрорадиоизмерений»

«Электрорадиоизмерения в мехатронике»

Под измерением понимается процесс количественного сравнения некоторого свойства объекта с мерой этого свойства или со стандартом (эталоном). Измерения делятся на прямые и косвенные. При прямом измерении результат получается непосредственно из измерения самой величины (например, измерение напряжения вольтметром, сопротивления — омметром). При косвенном измерении искомое значение величины находится по известной зависимости между ней и непосредственно измеряемыми величинами. Таким образом, любое косвенное измерение сводится к совокупности прямых измерений (например, нахождение мощности постоянного тока по измеренным напряжению и силе тока).

Помимо результата измерения важной информативной характеристикой является погрешность измерения, показывающая отклонение результата измерения от истинного значения физической величины.
1 ОБЩИЕ СВЕДЕНИЯ

1.1 При подключении измерительного прибора необходимо учитывать влияние прибора на параметры исследуемой схемы и стремиться свести это влияние к минимуму.

Вольтметры и осциллографы подключаются параллельно входу, выходу или промежуточным точкам схемы, поэтому входное сопротивление этих приборов должно быть намного больше внутреннего сопротивления измеряемого участка. Необходимо также учитывать, что входное сопротивление измерительного прибора имеет активную и реактивную составляющую. Для уменьшения влияния приборов их часто подключают к измеряемым точкам через развязывающие конденсаторы или резисторы, учитывая при этом величину падения напряжения на них.

1.2 При измерениях необходимо учитывать погрешность приборов, которая связана с классом точности. Для большинства из них он выражает отношение абсолютной погрешности измерения к пределу измерения в процентах и принадлежит к ряду чисел 0.05; 0.1; 0.2; 0.5; 1.0; 1.5; 2.5; 4.0.

1.3 Электрические измерительные приборы в зависимости от характера измеряемых величин разделяются на подгруппы, которым присваиваются буквенные значения. Приборам подгруппы к буквенному обозначению прибавляется цифровое, обозначающее вид выполняемой функции. Далее через дефис в обозначение входит число, указывающее номер модели в зависимости от очередности разработки.

1.3.1 Подгруппа А — это приборы для измерения силы тока: А1 — установки для поверки амперметров; А2, A3, A7 — соответственно амперметры постоянного, переменного токов и универсальные.

1.3.2 Подгруппа Б — это источники питания; Б2, Б4, Б5, Б6, Б7 — источники переменного тока, калиброванного напряжения и тока, постоянного тока, с регулированными параметрами, универсальные.

1.3.3 Подгруппа В — это приборы для измерения напряжения; В1 — установки для поверки вольтметров; В2, В3, В4, В5, В6, В7 — вольтметры постоянного, переменного, импульсного токов, фазочувствительные, селективные и универсальные соответственно; В8 — измерители отношений напряжений; В9 — преобразователи напряжений.

1.3.4 Подгруппа Г — это измерительные генераторы; Г1 — установки для поверки генераторов; Г2, Г3, Г4, Г5, Г8 — генераторы шумовые, низкочастотные, специальной формы, импульсные, качающейся частоты.

1.3.5 Подгруппа Е — приборы для измерения параметров компонентов и цепей; Е1 — установки для поверки измерителей параметров; Е2, Е3, Е4, Е5, Е6, Е7, Е8 — измерители полных сопротивлений, индуктивности, добротности, сопротивлений, универсальные, емкости.

1.3.6 Подгруппа Л — это приборы для измерения параметров электронных ламп и полупроводниковых приборов.

1.3.7 Подгруппа М — это приборы для измерения мощностей.

1.3.8 Подгруппа П — это приборы для измерения напряженности поля и радиопомех.

1.3.9 Подгруппа Р — это приборы для измерения параметров элементов с распределенными параметрами.

1.3.10 Подгруппа С — это приборы для наблюдения, измерения и исследования формы сигнала и спектра; С1, С7, С8, С9 — осциллографы универсальные, скоростные, запоминающие, специальные соответственно; С4 — анализаторы спектра.

1.3.11 Подгруппа Ч — это приборы для измерения частоты и времени.

В лабораторном практикуме необходимы навыки работы с измерителями токов, напряжений и сопротивлений, которые чаще всего используются, поэтому они обычно объединяются конструктивно (такие приборы называются комбинированными или АВО-метрами (ампервольтомметрами) или мультиметрами, их разнообразие очень велико); осциллографами; источниками сигналов (блоки питания и генераторы).

При измерениях мультиметром необходимо помнить о том, что измерения токов и сопротивлений требует переключения измерительных щупов (одного или двух) в различные гнезда. Кроме того, необходимо установить нужный диапазон и режим измерения с помощью переключателей на приборе.

3. Статистическая обработка результатов измерений

При статистической обработке результатов прямых многократных измерений выполняют следующие операции:

— исключают известные систематические погрешности из результатов измерений;

— вычисляют оценку измеряемой величины;

— вычисляют среднее квадратическое отклонение результатов измерений;

— проверяют наличие грубых погрешностей и при необходимости исключают их;

— проверяют гипотезу о принадлежности результатов измерений нормальному распределению;

— вычисляют доверительные границы случайной погрешности (доверительную случайную погрешность) оценки измеряемой величины;

— вычисляют доверительные границы погрешности оценки измеряемой величины.

Для определения доверительных границ погрешности оценки измеряемой величины доверительную вероятность принимают равной 0,95.

Оценка измеряемой величины и среднее квадратическое отклонение

5.1 Оценку измеряемой величины , за которую принимают среднее арифметическое значение результатов измерений, вычисляют по формуле

, (1)

где — -й результат измерений;

— число результатов измерений.

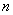
5.3 Среднее квадратическое отклонение группы, содержащей результатов измерений, вычисляют по формуле

. (3)

Примечание — Наличие случайных погрешностей вызывает рассеяние результатов измерений. В качестве основной числовой характеристики случайного рассеяния результатов измерений принята дисперсия или стандартное отклонение . Ограниченное число результатов измерений позволяет получать лишь оценки этих характеристик ( и ). Математическое ожидание оценки равно дисперсии , однако математическое ожидание оценки отлично от , так как оценка смещена.

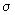
Несмещенную оценку допускается вычислять по упрощенной формуле

.

В этом случае смещение оценки не более 1%.

5.4 Среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины) 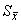вычисляют по формуле

. (4)

Источник

2.6. Обработка результатов измерений

Обработка прямых измерений. Для характеристики большинства приборов часто используют понятие приведенной погрешности, равной абсолютной погрешности в процентах диапазона шкалы измерений. По приведенной погрешности приборы разделяются на классы точности. Класс точности указан на панели прибора.

Наибольшая инструментальная погрешность измеряется по формуле:

,               (2.1)

где К – класс точности, А – наибольшее значение шкалы прибора.

Инструментальную погрешность невозможно уменьшить статистической обработкой отсчетов.

При наличии случайных погрешностей наблюдаемые значения измеряемой величины при многократных измерениях случайным образом рассеяны относительно ее истинного значения. В этом случае действительное значение находят как наиболее вероятное из серии отсчетов, а погрешность характеризуют шириной интервала, который с заданной вероятностью показывает истинное значение [44].

Наилучшей оценкой истинного значения величины Х является выборочное среднее значение

,                    (2.2)

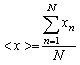
где   – отсчет величины Х,  – число отсчетов.

Для оценки разброса отсчетов при измерении используется выборочное среднее квадратическое отклонение отсчетов

.           (2.3)

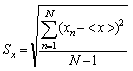
Выборочное среднее является случайной величиной и его разброс относительно истинного значения измеряемой величины оценивается выборочным средним квадратическим отклонением среднего значения

.                          (2.4)

Доверительным интервалом называется интервал , который с заданной степенью достоверности включает в себя истинное значение измеряемой величины.

Доверительной вероятностью (надежностью) результата серии наблюдений называется вероятность , с которой доверительный интервал включает истинное значение измеряемой величины.

Случайную составляющую погрешности принято выражать как полуширину доверительного интервала. Случайная составляющая погрешности многократных измерений

,                (2.5)

где  – безразмерный коэффициент доверия (коэффициент Стьюдента).

Чем больше доверительная вероятность, тем надежнее оценка интервала и, вместе с тем, шире его границы.

Полная абсолютная погрешность  прямых измерений равна квадратической сумме ее составляющих: инструментальной –  и случайной –

 .        (2.6)

Полная относительная погрешность  прямых измерений равна отношению полной абсолютной погрешности к выборочному среднему значению

.            (2.7)

Обработка косвенных измерений [44]. Расчет погрешностей косвенных измерений осуществляется по алгоритму, использующему сложение абсолютных величин погрешностей.

Пусть  – функциональная зависимость между измеряемой величиной  и величинами , значения которых найдены прямыми измерениями. Действительное значение  определяется как:

.       (2.8)

Вычисляем относительные погрешности аргументов. Затем определяем абсолютную и относительную погрешности функции

                        (2.9)

и по формулам:

—          для относительной погрешности

;                 (2.10)

—          для абсолютной погрешности

.                           (2.11)

Оценка токсического действия тестируемой пробы воды. Оценка токсического действия тестируемой пробы воды делается на основании достоверности различий между показателями прироста численности клеток водорослей в контроле и в опыте. При этом вычисляют [14]:

– средние арифметические величины прироста численности клеток – X_i и X (в контроле и опыте);

– среднее квадратичное отклонение  по формуле (2.3);

– ошибку среднего арифметического (X):

– Td – критерий достоверности различий двух величин:

;                       (2.12)

,              (2.13)

где x_k и x_о – сравниваемые средние величины (в контроле и опыте),

Sk² и So² – квадраты ошибок средних в контроле и опыте.

Td рассчитывают для каждой тестируемой пробы и сравнивают с табличной величиной Tst – стандартным значением критерия Стьюдента. В нашем случае для его определения принимаем уровень значимости р = 0,05 (95%) и степень свободы = (n1 + n2 – 2), т. е. (3 + 3 – 2) = 4. Tst при степени свободы 4 равно 2,78.

Если Td ≥ Tst, то различие между контролем и опытом достоверно – тестируемая вода загрязнена.

Если Td < Tst, то различие между контролем и опытом не достоверно – тестируемая вода не загрязнена.