НОД чисел онлайн
Наибольшим общим делителем нескольких натуральных чисел называется наибольшее натуральное число на которое делятся эти числа без остатка
Выберите количество чисел для нахождения НОД
2 числа3 числа4 числа5 чисел6 чисел
Введите числа
Нахождение НОД с помощью разложения на простые множители
1) Для начала нужно каждое число разложить на простые множители
2) Потом подчеркнуть общие множители
3) Перемножить все общие множители
4) Результатом умножения общих множителей будет НОД
Разберём пример
Найдём НОД(8,16)
Разложим числа
8 = 2 × 2 × 2
16 = 2 × 2 × 2 × 2
Подчеркнём общие множители
8 = 2 × 2 × 2
16 = 2 × 2 × 2 × 2
Перемножим общие множители
НОД(8, 16) = 2 × 2 × 2 = 8
Нод 3 чисел и более
Всё по аналогии с 2 числами
Разберём пример
Найдём НОД(8,16,32)
Разложим числа
8 = 2 × 2 × 2
16 = 2 × 2 × 2 × 2
32 = 2 × 2 × 2 × 2 × 2
Подчеркнём общие множители
8 = 2 × 2 × 2
16 = 2 × 2 × 2 × 2
32 = 2 × 2 × 2 × 2 × 2
Перемножим общие множители
НОД(8, 16, 32) = 2 × 2 × 2 = 8
Что может калькулятор ?
Находить НОД 2 чисел
Находить НОД 3 чисел
Находить НОД 4 чисел
Находить НОД 5 чисел
Находить НОД 6 чисел
Отображает алгоритм нахождения НОД
Похожие калькуляторы
Как найти НОД
- Нахождение путём разложения на множители
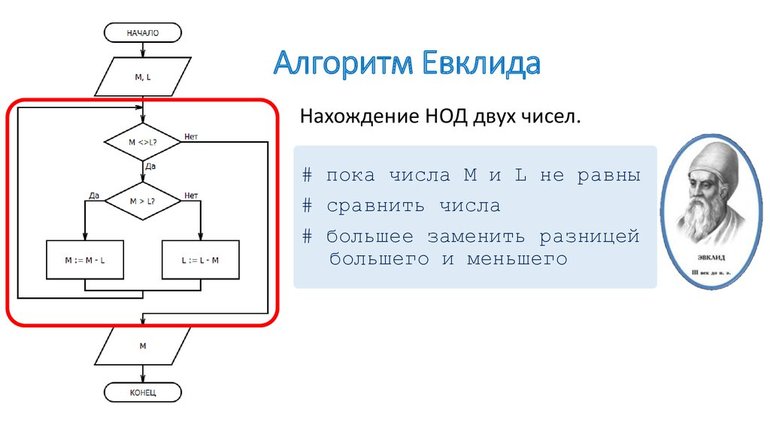
- Алгоритм Евклида
Рассмотрим два способа нахождения наибольшего общего делителя.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.
Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.
Пример 1. Найти НОД (84, 90).
Решение: Раскладываем числа 84 и 90 на простые множители:
Итак, мы подчеркнули все общие простые множители, осталось перемножить их между собой:
2 · 3 = 6.
Таким образом, НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
Решение: Раскладываем 15 и 28 на простые множители:
Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.
НОД (15, 28) = 1.
Алгоритм Евклида
Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.
Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.
Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.
Пример 1. Возьмём два числа 27 и 9. Так как 27 делится на 9 и 9 делится на 9, значит, 9 является общим делителем чисел 27 и 9. Этот делитель является в тоже время и наибольшим, потому что 9 не может делиться ни на какое число, большее 9. Следовательно:
НОД (27, 9) = 9.
В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:
- Из двух данных чисел большее число делят на меньшее.
- Затем, меньшее число делят на остаток, получившийся от деления большего числа на меньшее.
- Далее, первый остаток делят на второй остаток, который получился от деления меньшего числа на первый остаток.
- Второй остаток делят на третий, который получился от деления первого остатка на второй и т. д.
- Таким образом деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель как раз и будет наибольшим общим делителем.
Пример 2. Найдём наибольший общий делитель чисел 140 и 96:
1) 140 : 96 = 1 (остаток 44)
2) 96 : 44 = 2 (остаток 
3) 44 : 8 = 5 (остаток 4)
4) 8 : 4 = 2
Последний делитель равен 4 — это значит:
НОД (140, 96) = 4.
Последовательное деление так же можно записывать столбиком:
Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:
- Сперва находим наибольший общий делитель любых двух чисел из нескольких данных.
- Затем находим НОД найденного делителя и какого-нибудь третьего данного числа.
- Затем находим НОД последнего найденного делителя и четвёртого данного числа и так далее.
Пример 3. Найдём наибольший общий делитель чисел 140, 96 и 48. НОД чисел 140 и 96 мы уже нашли в предыдущем примере (это число 4). Осталось найти наибольший общий делитель числа 4 и третьего данного числа — 48:
48 : 4 = 12
48 делится на 4 без остатка. Таким образом:
НОД (140, 96, 48) = 4.
Калькулятор онлайн.
Нахождение (вычисление) НОД и НОК
Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей.
Пример: для чисел 6 и 9 наибольший общий делитель равен 3.
Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не равно нулю.
В школьной программе обозначается так: НОД(m, n)
Понятие наибольшего общего делителя (НОД) распространяется на любой набор из более чем двух целых чисел.
Чаще всего НОД используется для сокращения дроби — если найти НОД числителя и знаменателя, то на это число можно сократить
числитель и знаменатель данной дроби.
Наименьшее общее кратное (НОК) двух целых чисел m и n это наименьшее натуральное число, которое делится на m и n без остатка.
В школьной программе обозначается так: НОК(m, n)
Пример: НОК(16, 20) = 80
Одно из наиболее частых применений НОК — приведение дробей к общему знаменателю.
С помощью данной математической программы вы можете найти (вычислить) НОД и НОК двух целых чисел.
Программа нахождения НОД и НОК не только выводит ответ задачи, но и отображает процесс вычисления НОД и НОК двух чисел.
Вводить можно только целые положительные числа.
Наши игры, головоломки, эмуляторы:
Немного теории.
Наибольший общий делитель (НОД). Взаимно простые числа
Определение. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют
наибольшим общим делителем (НОД) этих чисел.
Найдём наибольший общий делитель чисел 24 и 35.
Делителями 24 будут числа 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут числа 1, 5, 7, 35.
Видим, что числа 24 и 35 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми.
Определение. Натуральные числа называют взаимно простыми, если их наибольший общий делитель (НОД) равен 1.
Наибольший общий делитель (НОД) можно найти, не выписывая всех делителей данных чисел.
Разложим на множители числа 48 и 36, получим:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа
(т. е. две двойки).
Остаются множители 2 * 2 * 3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36.
Так же находят наибольший общий делитель трёх и более чисел.
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произ ведение оставшихся множителей.
Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Например, наибольшим общим делителем чисел 15, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.
Наименьшее общее кратное (НОК)
Определение. Наименьшим общим кратным (НОК) натуральных чисел а и b называют наименьшее натуральное число,
которое кратно и a и b.
Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на
простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения
второго числа (т.е. объединяем множители).
Получаем пять множителей 2 * 2 * 3 * 5 * 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трёх и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных
чисел.
Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа.
Пифагор (VI в. до н. э.) и его ученики изучали вопрос о делимости чисел. Число, равное сумме всех его делителей (без самого числа),
они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные
числа — 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвёртое — 8128 — стало известно в I в. н. э.
Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор учёные не знают, есть ли
нечётные совершенные числа, есть ли самое большое совершенное число.
Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представлено в виде
произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа.
Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются неравномерно — в одних частях ряда их больше,
в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует
ли последнее (самое большое) простое число? Древнегреческий математик Евклид (III в. до н. э.) в своей книге «начала», бывшей на
протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом
есть ещё большее простое число.
Для отыскания простых чисел другой греческий математик того же времени Эратосфен придумал такой способ. Он записывал все числа
от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом, затем вычёркивал через
одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее
вычёркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). в конце концов оставались
невычеркнутыми только простые числа.
Наибольшим общим делителем (НОД) двух целых чисел называется наибольший из их общих делителей. К примеру для чисел 12 и 8, наибольшим общим делителем будет 4.
Как найти НОД?
Способов найти НОД несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОД при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:
- разложить оба числа на простые множители (подробнее о разложении чисел на простые множители смотрите тут);
- выбрать одинаковые множители, входящие в оба разложения;
- найти их произведение.
Примеры нахождения наибольшего общего делителя
Рассмотрим приведенный алгоритм на конкретных примерах:
Пример 1: найти НОД 12 и 8
1. Раскладываем 12 и 8 на простые множители:
2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 2 и 2
3. Перемножаем эти множители и получаем: 2 · 2 = 4
Ответ: НОД (8; 12) = 2 · 2 = 4.
Пример 2: найти НОД 75 и 150
Этот пример, как и предыдущий с легкостью можно высчитать в уме и вывести ответ 75, но для лучшего понимания работы алгоритма, проделаем все шаги:
1. Раскладываем 75 и 150 на простые множители:
2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 3, 5 и 5
3. Перемножаем эти множители и получаем: 3 · 5 · 5 = 75
Ответ: НОД (75; 150) = 3 · 5 · 5 = 75.
Частный случай или взаимно простые числа
Нередко встречаются ситуации, когда оба числа взаимно простые, т.е. общий делитель равен единице. В этом случае, алгоритм будет выглядеть следующим образом:
Пример 3: найти НОД 9 и 5
1. Раскладываем 5 и 9 на простые множители:
Видим, что одинаковых множителей нет, а значит, что это частный случай (взаимно простые числа). Общий делитель — единица.
Понятие НОД
Определение, что такое НОД в математике, звучит следующим образом: наибольший делитель, общий для чисел a и b, есть такое наибольшее число, на которое описанные значения смогут разделиться без остатка.
Для наилучшего понимания того, как найти НОД двух чисел, вместо указанных переменных достаточно подставлять простые числа, например, 12 и 9. То есть самым наименьшим делимым числом для 12 и 9 является то, которое позволяет найти решение без остатка.
Задача по нахождению НОД может решаться тремя способами. Каждый из них применяется в зависимости от того, насколько быстро требуется найти необходимый показатель:
- Первый метод схож с алгоритмом Евклида для нахождения НОД. Он достаточно трудоемкий и канонический. Необходимо искать все возможные делители, а через них — наибольший делитель, являющийся общим для значений. Если выписывать все показатели, на которые поделятся 12 и 9, наибольшим окажется 3.
- Второй способ предполагает разложение пары чисел на простые множители и перемножение наибольших из них между собой.
- Суть следующего способа: компоненты, которые подлежат поиску наибольшего общего делителя, начинают раскладывать на простые множители. Это значит, что из разложения первого нужно вычеркнуть множители, какие не попадают во второе значение. Остальные показатели в первом разложении перемножаются и оказываются НОД.
Лучше всего рассматривать применение указанных методов через определенный класс задач, которые помогают при дальнейшем изучении теорем, касающихся дробей. Формулы для указанной темы очень доступны для понимания ученикам и учителям.
Метод разложения
Суть второй методики заключается в разложении на простые множители и перемножении общих из них. В качестве примера можно рассмотреть представление НОД для показателей 18 и 24:
- Оба параметра раскладываются на множители — 24 на 1, 2, 3, 4, 6, 8, 12, 24, а 18 на 1, 2, 3, 6, 9, 18. Происходит поиск общих значений.
- Необходимо перемножать между собой общие множители. Если есть риск запутаться, то стоит подчеркивать общие значения.
- В результате поиска соотношений выделяют в качестве общих значений 2 и 3. После перемножения они дают число 6. Именно это линейное число и считается наибольшим объединенным делителем.
Способ является достаточно простым. Однако из-за некоторого объема операций можно оказаться в сложной ситуации с поиском общих делителей, поэтому следует рассмотреть еще один способ.
Вычеркивание показателей
Для третьей методики характерно вычеркивание из разложения тех показателей, которые не проходят во второе число. Есть такие виды НОД, которые могут сильно отличаться, но все равно позволяют найти нужный показатель. Например, нужно найти наибольший делитель для значений 28 и 16:
- Сначала раскладывают оба параметра на простые множители. Для 28 таковыми считаются 1, 2, 4, 7, 14, 28, для 16 это 1, 2, 4, 8,16.
- Из разложения первого объекта по формуле следует вычеркнуть показатель 7, так как он не входит в группу делителей второго.
- После перемножения наибольшим делителем оказывается 4. Проверка в виде деления на него 28 и 16 показывает, что именно он и является нужным НОДом.
Аналогично можно отыскать для других значений, например, 100 и 40. После разложения из первого перечеркивается лишняя пятерка. Перемножение дает 20, который после поверки оказывается наибольшим делителем.
Несколько значений
Несмотря на кажущуюся сложность, доказать, что возможно найти НОД для нескольких чисел без помощи онлайн-калькуляторов, вполне реально. Значения, подлежащие поиску, необходимо разложить на множители. После чего ищется произведение общих простейших множителей.
Есть такие числа как 18, 24 и 36. Разложение 18 дает такие коэффициенты как 1, 2, 3, 6, 9 и 18. Затем 24 и 36 необходимо править по аналогичному методу. Если составить таблицу, то можно найти следующие общие показатели в виде 2 и 3. Они считаются общими для всех трех чисел.
Перемножив между собой, получается делимое число 6. Оно также подходит под разложение 18, 24 и 36, а также считается наибольшим общим делителем для всех трех параметров. Аналогичный принцип срабатывает и для четырех и более чисел, когда потребуется найти делитель на любом уровне сложности вплоть до максимального.
Наименьшее общее кратное
Помимо НОД, существует еще и наименьшее общее кратное, или НОК. Если сказать по-другому, то таковым свойством можно считать число, которое без остатка будет разделяться на число a и число b.
Как и для НОД, поиск НОК может осуществляться тремя похожими с предшествующими способами. Каждым из них можно воспользоваться в зависимости от ситуации и удобства решения задания:
- Первый метод достаточно простой и распространенный. Необходимо записать кратные первых чисел, после чего подобрать такое число, чтобы оно являлось общим для всех и наименьшим.
- Также возможно раскладывать кратные на простые натуральные множители. В этом случае переписываются множители из первого разложения и прибавляются недостающие во второе. Получаемые значения перемножают между собой и получают НОК.
- Особняком стоит третий метод, который работает при соблюдении определенных условий. Одним из них является то, что НОК ищут для двух чисел, и на предыдущих этапах был найден наибольший общий делитель.
На последнем методе стоит остановиться несколько подробнее. Он является не только сравнительно менее громоздким, но и обладает определенным преимуществом в виде уже найденного НОД и более простого алгоритма решения.
Совмещение делителей
Такая методика характерна для тех примеров, в которых требуется единовременное нахождение НОД и НОК двух чисел. Например, необходимо отыскать для чисел 24 и 12 НОК и НОК. Действовать нужно в следующем порядке:
- Первым делом нужно найти НОД. Для этого надлежит раскладывать оба числа, отыскать общий показатель 12.
- После этого 24 и 12 перемножаются между собой. Результатом становится 288.
- Полученное число требуется разделять на НОД от 24 и 12. Полученный ответ 24 говорит о том, что именно оно является наименьшим общим кратным для 24 и 12.
Сходный механизм действует и при поиске НОК и НОД исходя из другой пары чисел. В каждом примере необходимо сначала отыскать наибольший делитель, перемножить два числа и получить наименьшее кратное.
Что касается решения с помощью интернет-ресурсов, то на сегодняшний день имеется много онлайн-калькуляторов и программ, которые дают возможность сравнительно быстро найти НОД и НОК и подсказать грамотные пути решения.
Нахождение наибольшего делителя и НОК является не только распространенной, но и сравнительно трудной задачей для учеников средней школы. Ведь если не рассмотреть подробно такую тему, то дальнейшее изучение дробей, которые включают в себя числитель и знаменатель, окажется практически невозможным.
Важно грамотно использовать ресурсы на специальных математических сайтах, где могут подробно и понятно объяснить разложение дробей и нахождение общих делителей. Бояться ошибиться в такой теме не стоит, поскольку при правильном подходе она пройдет достаточно быстро, а вычисление различных по уровню сложности примеров не составит особых сложностей.