Как найти наибольший объем конуса - AvtoShod.ru - решение различных проблем

Ответ:

V = 6224,272 * √3 π см³

Объяснение:

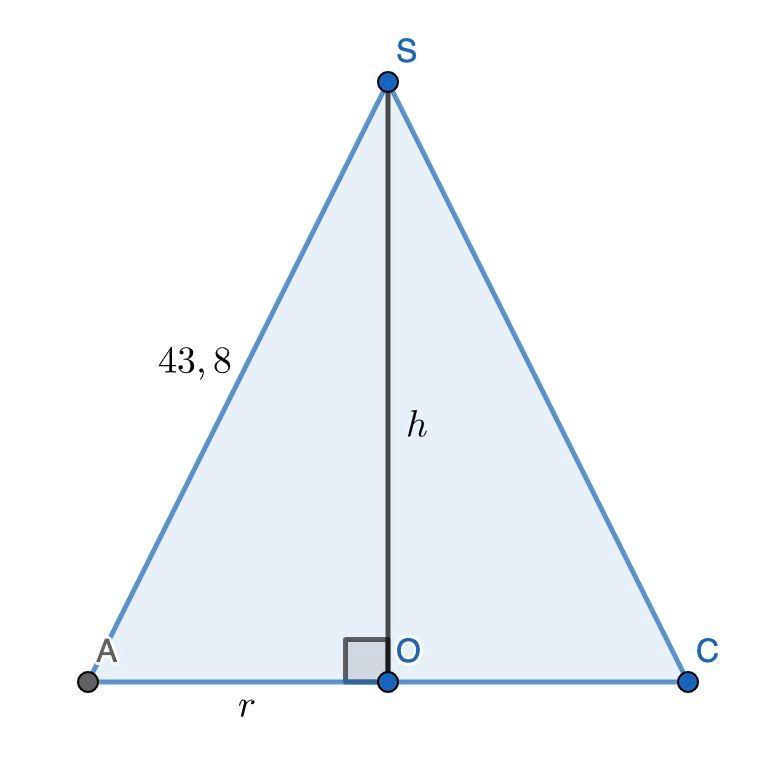
Рассмотрим осевое сечение конуса (см. рис.). SO — высота конуса (h), AO — радиус (r), AS — образующая конуса (43,8 см). Тогда по теореме Пифагора r² + h² = 43,8².

Объём конуса вычисляется по формуле $V=dfrac{1}{3}pi r^2h$ . Из предыдущего уравнения r² = 43,8² — h². Подставим это в уравнение объёма:

$V=dfrac{1}{3}pi (43{,}8^2-h^2)h=dfrac{43{,}8^2pi}{3}h-dfrac{pi}{3}h^3$

Найдём максимальное значение с помощью производной:

$V'(h)=dfrac{43{,}8^2pi}{3}-pi h^2\V'(h)=0Leftrightarrow dfrac{43{,}8^2pi}{3}=pi h^2Leftrightarrow h=pmdfrac{43{,}8}{sqrt{3}}$

Будем рассматривать только положительные значения h, так как отрицательной высота быть не может. При $0<h<dfrac{43{,}8}{sqrt{3}} V'(h)>0$ , при $h>dfrac{43{,}8}{sqrt{3}} V'(h)<0$ . Значит, $h=dfrac{43{,}8}{sqrt{3}}$ — точка максимума. При данном значении h объём конуса максимален.

$V_{max}=dfrac{1}{3}pileft(43{,}8^2-dfrac{43{,}8^2}{3}right)cdotdfrac{43{,}8}{sqrt{3}}=dfrac{1}{3}pi cdotdfrac{2}{3}cdot 43{,}8cdot 43{,}8cdotdfrac{43{,}8}{3}sqrt{3}=\=14{,}6cdot 2cdot 14{,}6cdot 14{,}6sqrt{3}pi=6224{,}272sqrt{3}pi$

Приложения:

Источник

Найти наибольший объем конуса

	28.10.2013, 02:49
Найти наибольший объем конуса, образующая которого имеет данную длину l.
1 2 3 4 5 Категория: Задачи на доказательство \| Добавил: alexlat
Просмотров: 4207 \| Загрузок: 0 \| Рейтинг: 5.0/1

Добавлять комментарии могут только зарегистрированные пользователи.

[

Регистрация

Вход

]

Статистика

Источник

Светило науки — 2752 ответа — 11053 помощи

Объём конуса V=π*R²*h, где R и h — радиус основания и высота конуса. По теореме Пифагора, R²+h²=l²=3 м², откуда R²=3-h² м². Тогда V= π*(3-h²)*h/3= π/3*(3*h-h³) м³. Производная V'(h)=π/3*(3-3*h²) м². Приравнивая её к нулю, приходим к уравнению π*(1-h²)=0, или 1-h²=0. Так как h>0, то h=1 м — критическая точка. При h<1 V'(h)>0, при h>1 V'(h)<0, поэтому точка h=1 является точкой максимума функции V(h), то есть объём конуса имеет наибольшее значение при h=1 м. Это значение Vmax=π*(3-1²)*1/3=2*π/3 м³. Ответ: 2*π/3 м³.

Источник

Найди верный ответ на вопрос ✅ «Решить задачу, используя понятия наибольшего наименьшего значения функции. Найти наибольший объем конуса, образующая которого равна l = √3 …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Главная » Математика » Решить задачу, используя понятия наибольшего наименьшего значения функции. Найти наибольший объем конуса, образующая которого равна l = √3 (м).

Источник

Объём конуса V = (1/3)π*R²*h, где R и h — радиус основания и высота конуса.

По теореме Пифагора, R² + h²=L², откуда R² = (L²- h²) м².

Тогда V = (π*( L² — h²)*h)/3 = (π/3)*( L²*h — h³) м³.

Производная V'(h) = (π/3)*( L² — 3h²).

Приравнивая её к нулю, приходим к уравнению (π/3)*( L² — 3h²) = 0.

Нулю приравниваем второе выражение в скобках.

Отсюда находим h = √(( L²)/3) = L/√3 = 44,7/√3 ≈ 25,80756 см.

Так как значение h положительно, то найденная точка h= (L/√3) является точкой максимума функции V(h).

Подставим значение h= (L/√3) в уравнение объёма:

V = (π/3)*( L²*(L/√3) — (L/√3)³) = (2πL³)/(9√3).

Значение Vmax = (2π*44,7³)/(9/√3) ≈ 35999,735 см³.