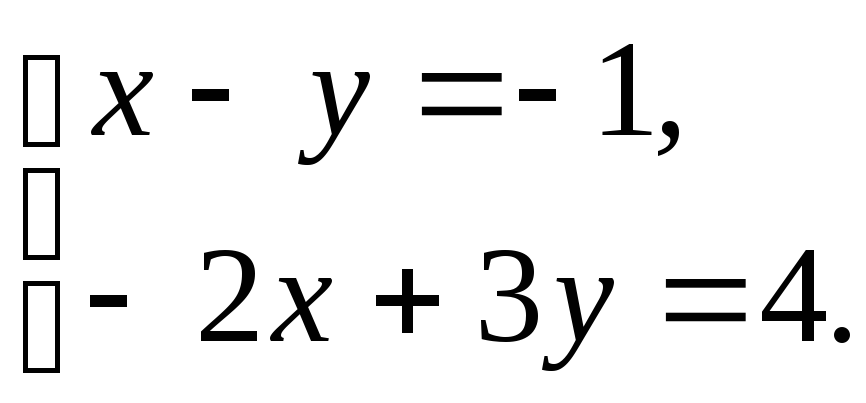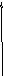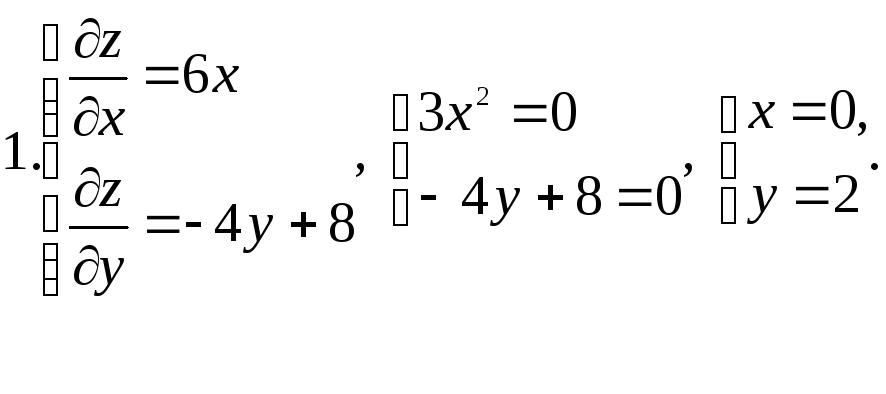Как найти наибольшее значение функции в области

Наибольшее и наименьшее значения функции двух переменных в замкнутой области.

Пусть функция $z=f(x,y)$ определена и непрерывна в некоторой ограниченной замкнутой области $D$. Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.

Алгоритм поиска наибольшего и наименьшего значений функции $z=f(x,y)$ в замкнутой области $D$.

1. Найти критические точки функции $z=f(x,y)$, принадлежащие области $D$. Вычислить значения функции в критических точках.
2. Исследовать поведение функции $z=f(x,y)$ на границе области $D$, найдя точки возможного наибольшего и наименьшего значений. Вычислить значения функции в полученных точках.
3. Из значений функции, полученных в предыдущих двух пунктах, выбрать наибольшее и наименьшее.

Что такое критические точки? показатьскрыть

Пример №1

Найти наибольшее и наименьшее значения функции $z=x^2+2xy-y^2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.

Решение

Будем следовать указанному выше алгоритму, но для начала разберёмся с чертежом заданной области, которую обозначим буквой $D$. Нам заданы уравнения трёх прямых, кои эту область ограничивают. Прямая $x=3$ проходит через точку $(3;0)$ параллельно оси ординат (оси Oy). Прямая $y=0$ – это уравнение оси абсцисс (оси Ox). Ну, а для построения прямой $y=x+1$ найдём две точки, через которые и проведём данную прямую. Можно, конечно, подставить вместо $x$ парочку произвольных значений. Например, подставляя $x=10$, получим: $y=x+1=10+1=11$. Мы нашли точку $(10;11)$, лежащую на прямой $y=x+1$. Однако лучше отыщем те точки, в которых прямая $y=x+1$ пересекается с линиями $x=3$ и $y=0$. Почему это лучше? Потому, что мы одним выстрелом уложим пару зайцев: получим две точки для построения прямой $y=x+1$ и заодно выясним, в каких точках эта прямая пересекает иные линии, ограничивающие заданную область. Прямая $y=x+1$ пересекает прямую $x=3$ в точке $(3;4)$, а прямую $y=0$ – в точке $(-1;0)$. Дабы не загромождать ход решения вспомогательными пояснениями, то вопрос о получении этих двух точек вынесу в примечание.

Как были получены точки $(3;4)$ и $(-1;0)$? показатьскрыть

Всё готово для построения чертежа, который будет иметь такой вид:

Вот теперь перейдём к первому шагу алгоритма. Найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=2x+2y-4; frac{partial z}{partial y}=2x-2y.
$$

Заметьте, что найденные производные первого порядка существуют для всех значений $x$ и $y$. Т.е. нету точек, в которых хотя бы одна производная не существует. Попробуем отыскать точки, в которых обе частные производные равны нулю (стационарные точки):

$$
left { begin{aligned}
& 2x+2y-4=0;\
& 2x-2y=0.
end{aligned} right.

;; left { begin{aligned}
& x+y=2;\
& x-y=0.
end{aligned} right.
$$

Мы получили систему линейных алгебраических уравнений. Для решения таких систем можно применить, например, метод Крамера. Однако в данном случае можно поступить попроще. Из второго уравнения имеем: $y=x$. Подставляя $y=x$ в первое уравнение, получим: $x+x=2$, $2x=2$, $x=1$. Так как $x=1$, то $y=x=1$. Итак, $(1;1)$ – единственная стационарная точка функции $z$.

Однако недостаточно просто найти стационарные точки. Нужно выбрать те из них, которые принадлежат области $D$. В нашем случае точка $(1;1)$ принадлежит этой области. Обозначим эту точку как $M_1(1;1)$. Вычислим значение функции в этой точке:

$$z_1=z(M_1)=1^2+2cdot 1cdot 1-1^2-4cdot 1=-2.$$

А почему точка $(1;1)$ принадлежит области $D$? показатьскрыть

Теперь настал черёд исследовать поведение функции на границе области, т.е. переходим ко второму шагу алгоритма. Начнём с прямой $y=0$.

Прямая $y=0$ (ось абсцисс) ограничивает область $D$ при условии $-1 ≤ x ≤ 3$. Подставим $y=0$ в заданную функцию $z(x,y)=x^2+2xy-y^2-4x$. Полученную в результате подстановки функцию одной переменной $x$ обозначим как $f_1(x)$:

$$
f_1(x)=z(x,0)=x^2+2xcdot 0-0^2-4x=x^2-4x.
$$

Теперь для функции $f_1(x)$ нужно найти наибольшее и наименьшее значения на отрезке $-1 ≤ x ≤ 3$. Отыщем производную этой функции и приравняем её к нулю:

$$
f_{1}^{‘}(x)=2x-4;\
2x-4=0; ; x=2.
$$

Значение $x=2$ принадлежит отрезку $-1 ≤ x ≤ 3$, поэтому к списку точек добавим ещё и $M_2(2;0)$. Кроме того, вычислим значения функции $z$ на концах отрезка $-1 ≤ x ≤ 3$, т.е. в точках $M_3(-1;0)$ и $M_4(3;0)$. Кстати, если бы точка $M_2$ не принадлежала рассматриваемому отрезку, то, разумеется, значение функции $z$ в ней вычислять не было бы надобности.

Итак, вычислим значения функции $z$ в точках $M_2$, $M_3$, $M_4$. Можно, конечно, подставлять координаты данных точек в исходное выражение $z=x^2+2xy-y^2-4x$. Например, для точки $M_2$ получим:

$$z_2=z(M_2)=2^2+2cdot 2cdot 0-0^2-4cdot 2=-4.$$

Однако вычисления можно немного упростить. Для этого стоит вспомнить, что на отрезке $M_3M_4$ имеем $z(x,y)=f_1(x)$. Распишу это подробно:

begin{aligned}
& z_2=z(M_2)=z(2,0)=f_1(2)=2^2-4cdot 2=-4;\
& z_3=z(M_3)=z(-1,0)=f_1(-1)=(-1)^2-4cdot (-1)=5;\
& z_4=z(M_4)=z(3,0)=f_1(3)=3^2-4cdot 3=-3.
end{aligned}

Разумеется, что в столь подробных записях обычно нет нужды, и все вычисления в дальнейшем станем записывать покороче:

$$z_2=f_1(2)=2^2-4cdot 2=-4;; z_3=f_1(-1)=(-1)^2-4cdot (-1)=5;; z_4=f_1(3)=3^2-4cdot 3=-3.$$

Теперь обратимся к прямой $x=3$. Эта прямая ограничивает область $D$ при условии $0 ≤ y ≤ 4$. Подставим $x=3$ в заданную функцию $z$. В результате такой подстановки мы получим функцию $f_2(y)$:

$$
f_2(y)=z(3,y)=3^2+2cdot 3cdot y-y^2-4cdot 3=-y^2+6y-3.
$$

Для функции $f_2(y)$ нужно найти наибольшее и наименьшее значения на отрезке $0 ≤ y ≤ 4$. Отыщем производную этой функции и приравняем её к нулю:

$$
f_{2}^{‘}(y)=-2y+6;\
-2y+6=0; ; y=3.
$$

Значение $y=3$ принадлежит отрезку $0 ≤ y ≤ 4$, поэтому к найденным ранее точкам добавим ещё и $M_5(3;3)$. Кроме того, нужно вычислить значение функции $z$ в точках на концах отрезка $0 ≤ y ≤ 4$, т.е. в точках $M_4(3;0)$ и $M_6(3;4)$. В точке $M_4(3;0)$ мы уже вычисляли значение $z$. Вычислим значение функции $z$ в точках $M_5$ и $M_6$. Напомню, что на отрезке $M_4M_6$ имеем $z(x,y)=f_2(y)$, поэтому:

begin{aligned}
& z_5=f_2(3)=-3^2+6cdot 3-3=6;
& z_6=f_2(4)=-4^2+6cdot 4-3=5.
end{aligned}

И, наконец, рассмотрим последнюю границу области $D$, т.е. прямую $y=x+1$. Эта прямая ограничивает область $D$ при условии $-1 ≤ x ≤ 3$. Подставляя $y=x+1$ в функцию $z$, будем иметь:

$$
f_3(x)=z(x,x+1)=x^2+2xcdot (x+1)-(x+1)^2-4x=2x^2-4x-1.
$$

Вновь мы получили функцию одной переменной $x$. И вновь нужно найти наибольшее и наименьшее значения этой функции на отрезке $-1 ≤ x ≤ 3$. Отыщем производную функции $f_{3}(x)$ и приравняем её к нулю:

$$
f_{3}^{‘}(x)=4x-4;\
4x-4=0; ; x=1.
$$

Значение $x=1$ принадлежит отрезку $-1 ≤ x ≤ 3$. Если $x=1$, то $y=x+1=2$. Добавим к списку точек ещё и $M_7(1;2)$ и выясним, чему равно значение функции $z$ в этой точке. Точки на концах отрезка $-1 ≤ x ≤ 3$, т.е. точки $M_3(-1;0)$ и $M_6(3;4)$, были рассмотрены ранее, значение функции в них мы уже находили.

$$z_7=f_3(1)=2cdot 1^2-4cdot 1-1=-3.$$

Второй шаг решения закончен. Мы получили семь значений:

$$z_1=-2;;z_2=-4;;z_3=5;;z_4=-3;;z_5=6;;z_6=5;;z_7=-3.$$

Обратимся к третьему шагу алгоритма. Выбирая наибольшее и наименьшее значения из тех чисел, что были получены в третьем пункте, будем иметь:

$$z_{min}=-4; ; z_{max}=6.$$

Задача решена, осталось лишь записать ответ.

Ответ: $z_{min}=-4; ; z_{max}=6$.

Пример №2

Найти наибольшее и наименьшее значения функции $z=x^2+y^2-12x+16y$ в области $x^2+y^2 ≤ 25$.

Решение

Сначала построим чертёж. Уравнение $x^2+y^2=25$ (это граничная линия заданной области) определяет окружность с центром в начале координат (т.е. в точке $(0;0)$) и радиусом 5. Неравенству $x^2+y^2 ≤ 25$ удовлетворяют все точки внутри и на упомянутой окружности.

Будем действовать по алгоритму. Найдем частные производные и выясним критические точки.

$$
frac{partial z}{partial x}=2x-12; frac{partial z}{partial y}=2y+16.
$$

Точек, в которых найденные частные производные не существуют, нет. Выясним, в каких точках обе частные производные одновременно равны нулю, т.е. найдём стационарные точки.

$$
left { begin{aligned}
& 2x-12=0;\
& 2y+16=0.
end{aligned} right. ;;
left { begin{aligned}
& x=6;\
& y=-8.
end{aligned} right.
$$

Мы получили стационарную точку $(6;-8)$. Однако найденная точка не принадлежит области $D$. Это легко показать, даже не прибегая к помощи рисунка. Проверим, выполняется ли неравенство $x^2+y^2 ≤ 25$, которое определяет нашу область $D$. Если $x=6$, $y=-8$, то $x^2+y^2=36+64=100$, т.е. неравенство $x^2+y^2 ≤ 25$ не выполнено. Вывод: точка $(6;-8)$ не принадлежит области $D$.

Итак, внутри области $D$ нет критических точек. Переходим дальше, ко второму шагу алгоритма. Нам нужно исследовать поведение функции на границе заданной области, т.е. на окружности $x^2+y^2=25$. Можно, конечно, выразить $y$ через $x$, а потом подставить полученное выражение в нашу функцию $z$. Из уравнения окружности получим: $y=sqrt{25-x^2}$ или $y=-sqrt{25-x^2}$. Подставляя, например, $y=sqrt{25-x^2}$ в заданную функцию, будем иметь:

$$
z=x^2+y^2-12x+16y=x^2+25-x^2-12x+16sqrt{25-x^2}=25-12x+16sqrt{25-x^2}; ;; -5≤ x ≤ 5.
$$

Дальнейшее решение будет полностью идентично исследованию поведения функции на границе области в предыдущем примере №1. Однако мне кажется более разумным в этой ситуации применить метод Лагранжа. Нас будет интересовать лишь первая часть этого метода. После применения первой части метода Лагранжа мы получим точки, в которых и исследуем функцию $z$ на предмет минимального и максимального значений.

Составляем функцию Лагранжа:

$$
F=z(x,y)+lambdacdot(x^2+y^2-25)=x^2+y^2-12x+16y+lambdacdot (x^2+y^2-25).
$$

Находим частные производные функции Лагранжа и составляем соответствующую систему уравнений:

$$
F_{x}^{‘}=2x-12+2lambda x; ;; F_{y}^{‘}=2y+16+2lambda y.\
left { begin{aligned}
& 2x-12+2lambda x=0;\
& 2y+16+2lambda y=0;\
& x^2+y^2-25=0.
end{aligned} right.
;; left { begin{aligned}
& x+lambda x=6;\
& y+lambda y=-8;\
& x^2+y^2=25.
end{aligned} right.
$$

Для решения этой системы давайте сразу укажем, что $lambdaneq -1$. Почему $lambdaneq -1$? Попробуем подставить $lambda=-1$ в первое уравнение:

$$
x+(-1)cdot x=6; ; x-x=6; ; 0=6.
$$

Полученное противоречие $0=6$ говорит о том, что значение $lambda=-1$ недопустимо. Вывод: $lambdaneq -1$. Выразим $x$ и $y$ через $lambda$:

begin{aligned}
& x+lambda x=6;; x(1+lambda)=6;; x=frac{6}{1+lambda}. \
& y+lambda y=-8;; y(1+lambda)=-8;; y=frac{-8}{1+lambda}.
end{aligned}

Полагаю, что тут становится очевидным, зачем мы специально оговаривали условие $lambdaneq -1$. Это было сделано, чтобы без помех поместить выражение $1+lambda$ в знаменатели. Т.е., чтобы быть уверенным, что знаменатель $1+lambdaneq 0$.

Подставим полученные выражения для $x$ и $y$ в третье уравнение системы, т.е. в $x^2+y^2=25$:

$$
left(frac{6}{1+lambda} right)^2+left(frac{-8}{1+lambda} right)^2=25;\
frac{36}{(1+lambda)^2}+frac{64}{(1+lambda)^2}=25;\
frac{100}{(1+lambda)^2}=25; ; (1+lambda)^2=4.
$$

Из полученного равенства следует, что $1+lambda=2$ или $1+lambda=-2$. Отсюда имеем два значения параметра $lambda$, а именно: $lambda_1=1$, $lambda_2=-3$. Соответственно, получим и две пары значений $x$ и $y$:

begin{aligned}
& x_1=frac{6}{1+lambda_1}=frac{6}{2}=3; ; y_1=frac{-8}{1+lambda_1}=frac{-8}{2}=-4. \
& x_2=frac{6}{1+lambda_2}=frac{6}{-2}=-3; ; y_2=frac{-8}{1+lambda_2}=frac{-8}{-2}=4.
end{aligned}

Итак, мы получили две точки возможного условного экстремума, т.е. $M_1(3;-4)$ и $M_2(-3;4)$. Найдём значения функции $z$ в точках $M_1$ и $M_2$:

begin{aligned}
& z_1=z(M_1)=3^2+(-4)^2-12cdot 3+16cdot (-4)=-75; \
& z_2=z(M_2)=(-3)^2+4^2-12cdot(-3)+16cdot 4=125.
end{aligned}

На третьем шаге алгоритма следует выбрать наибольшее и наименьшее значения из тех, что мы получили на первом и втором шагах. Но в данном случае выбор невелик Имеем:

$$
z_{min}=-75; ; z_{max}=125.
$$

Ответ: $z_{min}=-75; ; z_{max}=125$.

1.Точкой
глобального максимума (минимума) функции
на множественазывается точка
,
в которой функция достигает своего
наибольшего или наименьшего значения

ТЕОРЕМА.
Пусть в
ограниченной и замкнутой области
задана дифференцируемая функция
.
Тогда эта функция достигает в области
D
своего наибольшего и наименьшего
значения (так называемый глобальный
экстремум).

Эти значения могут достигаться либо
в критических точках внутри области,
либо на ее границе. Поэтому внутри
области
нужно найти все точки, в которых возможен
экстремум. Затем, не выясняя, имеет ли
функцияв этих точках экстремум, вычислить
значения функции во всех найденных
точках. Однако функция может принимать
наибольшее и наименьшее значения и на
границе области. Поэтому нужно отдельно
найти наибольшее и наименьшее значения
функции на границе области. При этом
надо использовать уравнения границы,
что позволяет уменьшить число независимых
переменных у функции и свести задачу к
исследованию функции одной переменной.
Сравнивая все полученные таким образом
значения функции, выбираем из них
наибольшее и наименьшее.

Типовой пример

Найти наибольшее
и наименьшее значения функции
в замкнутой области (D),
заданной неравенствами
,

,

.

►Изобразим
область (D);
она представляет собой треугольник с
вершинами A|(-1;
-2), B(-1;
5), C(6;
-2). Найдём стационарные точки.
,
.
Решим систему уравнений

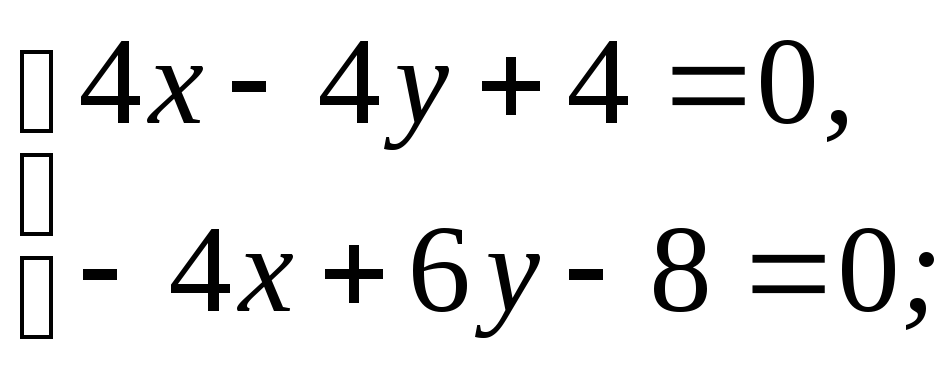
Решением этой
системы является x=1,
y=2.
Стационарная точка M(1;2)
принадлежит области (D),
так как её координаты удовлетворяют
всем трём неравенствам, задающим
треугольник (D).
Найдём значение функции в этой точке:
u(M)
= 2 – 8 + 12 + 4 – 16 + 5 = –1.

Исследуем функцию
на границе
области
(D).
Граница
представляет собой объединение трёх
отрезков:– отрезкаBC,
– отрезкаAB,
– отрезкаAC.

1)
.
=
2x²
– 4x(4
– x)
+

+ 3(4 – x)²
+ 4x
– 8(4–x)
+ 5 = 2x²
– 16x
+ 4x²
+ 3(16 – 8x
+ x²)
+ 4x
–

– 32 + 8x
+ 5 = 9x²
– 28x
+ 21. Найдём наибольшее и наименьшее
значения функции
9x²
– 28x
+ 21 на отрезке [–1; 6]. Имеем
18x
– 28; x
= 14/9 – стационарная точка функции
,
14/9

[–1; 6]. Обозначим N₁(14/9
; 4 –14/9 ) или N₁(14/9
; 22/9 ). u(N₁)
= ==196/9
– 392/9 + 21 = –34/9. Найдём значенияна концах отрезка [–1; 6]:=u(B)
= 58;
=u(C)
= 177. Наибольшим из этих значений является
u(C)
= 177, наименьшим – u(N₁)
= – 34/9.

2). =
2 + 4y
+ 3y²
– 4 – 8y
+

+5 = 3y²
– 4y
+ 3. Найдём наибольшее и наименьшее
значения функции
=
3y²
– 4y
+ 3 на отрезке [–2; 5];
=
6y
– 4; y
= 2/3 – стационарная точка функции
,
принадлежащая отрезку [–2; 5]. ОбозначимN₂(–1;
2/3). U(N₂)
=
.
Найдём значения функциина концах отрезка [– 2; 5]:=u(A)
= 23;
=u(B)
= 58.

3)
.
=
2x²
+ 8x
+ 12 + 4x
+ + 16 + 5 = 2x²
+ 12x
+ 33. Обозначим
=
2x²
+ 12x
+ 33.

= 4x
+ 12. Стационарная точка x
= – 3 не принадлежит отрезку

[–1; 6], поэтому она
нас не интересует. Значения
на концах отрезка

[–1; 6] были найдены
ранее:
=u(A)
= 23,
=u(C)
= = 177.

Сравнивая все
полученные значения, находим
=u(C)
=
= u(6;
–2) = 177,
=
u(M)
= u(1;
2) = – 1. ◄

Типовой пример

Найти наибольшее
и наименьшее значения функции
в области,
заданной неравенствами:,.

►1.
Изобразим область:

2. Точка
не принадлежит области.

3. Граница
областисостоит из трех гладких частейгдеизаданы уравнениями:.

3.1. На части
границы,
следовательно на,
где.
Теперь встала задача нахождения
наибольшего и наименьшего значения
функции одной переменнойна промежутке.
Так как,
то точкаявляется стационарной точкой функции,
и эта точка при­надлежит промежутку.
Этому значению переменнойнасоответст­вует значение.
Соответствующая точка —.

3.2. На части
границы,
следовательно, на,
где.
Исследуем функциюна промежутке.
Так как,
то точкаявляется стационарной точкой функции,
но эта точка не принадлежит промежутку.

3.3. На части
границы,
следовательно на,
где.
Исследуем функциюна промежутке.
Так как,
то точкаявляется стационарной точкой функции,и
эта точка принадлежит промежутку.
Соответствующая точка.

4. Таким образом,
имеется всего пять точек, в которых
нужно вычис­лить значения функции
:;;;;.
В результате вычислений получаем:;;;;.
Следовательно,,.
◄

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #