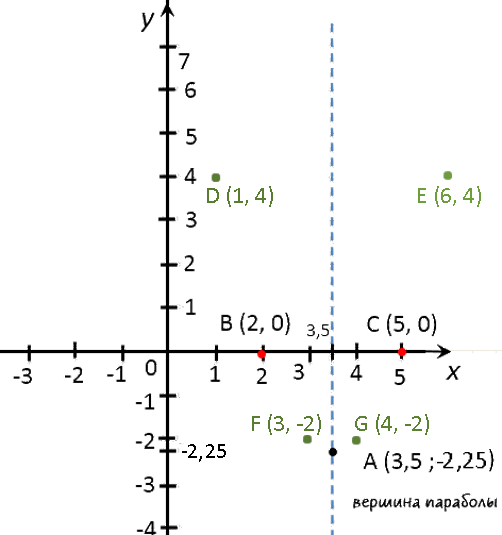Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a < 0», то ветви направлены вниз.
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
- Координаты вершины параболы
Запомните!
Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy». - Нули функции
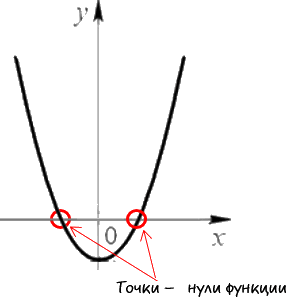
Для начала давайте разберемся, что называют нулями функции.
Запомните!
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.
- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график.
На забудьте после построения подписать график функции. - y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
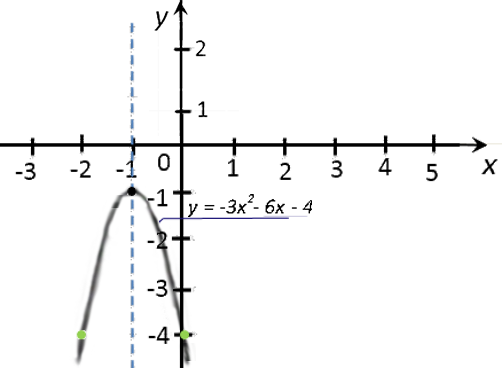
Пусть требуется построить график функции
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
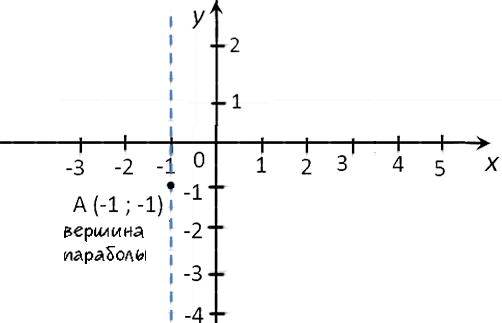
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Вершина параболы
Содержание:
- Что такое вершина параболы
- Вывод формулы координат вершины параболы
- Как найти координаты, основные способы
- Примеры решения задач
Что такое вершина параболы
Определение
Вершина параболы — это точка, в которой наблюдается пересечение параболой оси координат и ее невозможность держать направление выше или ниже в координатной плоскости.
Чтобы найти ВП, необходимо применить формулу:
(lbrackfrac{-b}{2a};-frac{b^2-4ac}{4a}rbrack)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Исходя из координат, можно узнать расположение вершины параболы и построить ее.
Вывод формулы координат вершины параболы
Рассматриваемую формулу используют для решения квадратных уравнений, которые имеют вид:
(y;=;ax^2;+;bx;+;c)
Ее график представляет собой параболу, формулу которой мы определили выше. Но не всегда требуется пользоваться данной формулой, так как сначала можно найти значение х, а затем подставить его в уравнение и найти y.
Для того, чтобы вывести формулу ВП, нужно преобразовать квадратную функцию к виду:
(y;=;f(x;+;l);+;m)
Делают это с помощью метода выделения полного квадрата, то есть (left(a+bright)^2) преобразуют в (a^2+2ab+b^2.)
Функции вида (y;=;f(x;+;l);+;m) отличаются от (y;=;f(x)) сдвигом из графиков по оси абсцисс на –l и по оси ординат на m. l в переписанной квадратичной функции равняется:
(frac{-b}{2a}, а frac{left(4ac-b^2right)}{4a})
Получается, что l и m — это координаты x0 и y0.
Приведем доказательство:
- Соединяем первые два члена многочлена: (y;=;(ax^2;+;bx);+;c.)
- Выносим коэффициент a за скобку, b при этом делим на a: (y=aleft(x^2+frac baxright)+c.)
- Представляем, что у нас есть квадрат суммы, в котором x является слагаемым, а из выражения в скобках необходимо рассчитать его полный квадрат суммы. Одночлен (frac bax) умножаем на два и делим на два одновременно. Далее прибавляем и вычитаем квадрат второго слагаемого квадрата суммы. Получаем: (y=aleft(x^2+2frac b{2a}x+frac{b^2}{4a^2}-frac{b^2}{4a^2}right)+c.)
- Выделяем квадрат суммы: (y=aleft(left(x+frac b{2a}right)^2-frac{b^2}{4a}right)+c.)
- Умножаем на a: (y=aleft(x+frac b{2a}right)^2-frac{b^2}{4a}+c.)
- Приводим свободные члены к общему знаменателю: (y=aleft(x+frac b{2a}right)^2-frac{b^2+4ac}{4a}.)
- Меняем знак: (y=aleft(x+frac b{2a}right)^2+frac{b^2-4ac}{4a}.)
Мы привели функцию (y;=;ax^2;+;bx;+;c) к виду (y;=;a{(x;+;l)}^2;+;m,) что соответствует (y;=;f(x;+;l);+;m,) где (f(x);=;ax^2. )
Как найти координаты, основные способы
Существует несколько способов нахождения координат ВП:
- (x_0=frac{-b}{2a}) — подходит в том случае, если дискриминант квадратного уравнения равен нулю.
- (y_0=-frac{b^2-4ac}{4a}) — это формула дискриминанта, поделенная на 4а.
- (x_0=frac{x_1+x_2}2) — среднее арифметическое между нулями функции. Можно использовать, если в выражении есть нули.
- Если функция имеет вид (y=aleft(x-x_0right)^2+y_0), то в ее вершиной совпадают координаты (left(x_0;y_0right).)
Примеры решения задач
Задача №1
Найти вершину параболы для уравнения: (y=x^2-5x+7.)
Решение: В выражение (x=-frac b{2a}) подставляем известные числа и получаем (x=frac52=2,5). Теперь подставляем x в исходное уравнение: (2,5^2-5times2,5+7=0,75.)
Ответ: (2,5; 0,75).
Задача №2
Найти ВП для уравнения: y=5(x-1)(x+7).
Решение: Ищем нули функции: 5(x-1)(x+7)=0. Тогда x-1=0 либо x+7=0. Из этого x=1; x=-7.
Подставляем и получаем: (x_0=frac{x_1+x_2}2=frac{1+left(-7right)}2=-3.)
Второе: (y_0=5timesleft(-3-1right)left(-3+7right)=-80.)
Ответ: (-3; -80).
Задача №3
Найти вершину параболы для уравнения: (y=x^2-7x+3 ).
Решение: (х_0=-frac b{2a}=-frac{left(-7right)}{2times1}=3,5.)
Второе: (y_0=3,5^2-7times3,5+3=-9,25.)
Ответ: (3,5; -9,25).
Насколько полезной была для вас статья?
Рейтинг: 2.50 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Содержание
- Основные понятия
- Построение квадратичной функции
- Как найти вершину параболы по формуле
- Алгоритм построения параболы
- Свойства и график квадратичной функции
- Уравнение квадратичной функции имеет вид y = ax2 + bx + c.
- Смещение параболы
- Уравнение параболы в полярной системе координат
- Как строить параболу по квадратному уравнению
- Гипербола
- Как определить, куда направлены ветви параболы
- Кривые второго порядка в высшей математике
- Окружность
- Эллипс
- Гипербола
- Парабола
- Методы нахождения координат вершины
- Уравнение квадратичной функции имеет вид y = a * (x — x₀)2 + y₀
- Исследование на плоскости уравнения второй степени
- Геометрический смысл параметра в уравнении параболы
- Пример решения
- Каноническое уравнение параболы
Основные понятия
Функция — это зависимость «y» от «x», где «x» — это переменная функции или аргумент, а «y» — зависимая переменная или значение функции.
Установка функции означает определение правила, согласно которому могут быть найдены соответствующие значения независимой переменной. Вот способы, которыми вы можете его установить:
- Табличный способ. Помогает быстро определять конкретные значения без дополнительных измерений или расчетов.
- Графический способ: понятно.
- Аналитическим путем, с помощью формул. Он компактен, и вы можете вычислить функцию для произвольного значения аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» вы можете подставить произвольные значения в функцию и найти координаты этих точек.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — числа, обязательное условие — 0. Уравнение имеет следующее распределение:
- а — главный коэффициент, отвечающий за ширину параболы. Большое значение a означает узкую параболу, маленькое значение означает большую параболу.
- b — второй коэффициент, отвечающий за смещение параболы от центра координат.
- c — свободный член, который соответствует координате пересечения параболы с осью y.
График квадратичной функции представляет собой параболу, которая при y = x2 имеет следующий вид:
Точки, отмеченные зелеными кружками, называются базовыми точками. Чтобы найти их координаты для функции y = x2, нужно создать таблицу:
| икс | -2 | −1 | 0 | 1 | 2 |
| да | 4 | 1 | 0 | 1 | 4 |
Если главный коэффициент в уравнении квадратной функции равен единице, график имеет ту же форму, что и y = x2 для любого значения остальных коэффициентов.
График функции y = –x2 имеет вид перевернутой параболы:
Зафиксируем координаты базовых точек в таблице:
| икс | -2 | −1 | 0 | 1 | 2 |
| да | −4 | −1 | 0 | −1 | −4 |
Глядя на оба графика, вы можете увидеть их симметрию относительно оси OX. Обращаем внимание на важные выводы:
- Если главный коэффициент больше нуля при> 0, ветви параболы направлены вверх.
- Если главный коэффициент меньше нуля при <0, ветви параболы направлены вниз.
Как построить график квадратичной функции: учитывать значения x, где функция равна нулю. В противном случае ее можно назвать нулевой функцией. На графике нули функции f (x) — это точки пересечения y = f (x) с осью OX.
Поскольку ордината (y) любой точки на оси OX равна нулю, следовательно, чтобы найти координаты точек пересечения графика функции y = f (x) с осью OX, необходимо решить уравнение е (х) = 0.
Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой необходимо решить квадратное уравнение ax2 + bx + c = 0. В процессе мы найдем дискриминант D = b2 — 4ac, который будет дают нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
Если a> 0, график выглядит так:
Исходя из вышеизложенного, ясно, что, зная направление ветвей параболы и знак дискриминанта, мы понимаем, как будет выглядеть график той или иной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим образом:
Ось симметрии параболы — это прямая линия, проходящая через вершину параболы параллельно оси OY.
Для построения графика нам понадобится точка пересечения параболы с осью OY. Поскольку абсцисса каждой точки на оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, вам нужно подставить ноль в уравнение вместо x: y (0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении показаны основные параметры графика квадратичной функции:
Как найти вершину параболы по формуле
Нахождение экстрима — главный шаг в решении многих практических задач. Конечно, можно открыть специальные онлайн-калькуляторы, но лучше уметь это делать самому.
Как вы можете это определить? Есть особая формула. Когда b не равно 0, вам нужно найти координаты этой точки.
Формулы поиска саммита:
- х0 = -b / (2 * а),
- у0 = у (х0).
Пример.
Есть функция y = 4 * x2 + 16 * x — 25. Находим вершины этой функции.
Для этой строки:
- х = -16 / (2 * 4) = -2,
- y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.
Получаем координаты вершины (-2, -41).
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в зависимости от того, как задана квадратичная функция.
Свойства и график квадратичной функции
Функция имеет ось симметрии и центр (крайний). Область определения: все значения по оси абсцисс.
Диапазон значений функции — (-∞, M) или (M, + ∞) зависит от направления ветвей кривой. Параметр M здесь указывает значение функции в верхней части строки.
Уравнение квадратичной функции имеет вид y = ax2 + bx + c.
Разберем общий алгоритм на примере y = 2×2 + 3x — 5.
Как мы строим:
- Определите направление ветвей параболы. Поскольку a = 2> 0, ветви параболы направлены вверх.
- Найдите дискриминант квадратного трехчлена 2×2 + 3x — 5.
D = b2 — 4ac = 9-4 * 2 * (-5) = 49> 0
√D = 7
В этом случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью OX. Чтобы найти их координаты, решаем уравнение:
2×2 + 3x — 5 = 0
- Координаты вершины параболы:
- Точка пересечения с осью OY составляет: (0; -5) и симметрична ей.
- Постройте эти точки на координатной плоскости и постройте параболу:
Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + bx + c второй и третий параметры равны 0 и = 1 — вершина находится в точке (0, 0).
Смещение по оси абсцисс или ординат связано с изменением параметров b и c соответственно. Перемещение линии по плоскости будет производиться ровно на то количество единиц, которое равно значению параметра.
Пример.
Имеем: b = 2, c = 3.
Это означает, что классическая форма кривой будет перемещать 2 единичных сегмента по абсциссе и 3 по ординате.
Уравнение параболы в полярной системе координат
Уравнение параболы в полярной системе координат (рис. 3.45, в) имеет вид
где — параметр притчи, а — ее эксцентриситет.
Действительно, в качестве полюса полярной системы координат выберем фокус параболы, а в качестве полярной оси — радиус с началом в точке, перпендикулярной директрисе и не пересекающей ее (рис. 3.45, в). Тогда для произвольной точки, принадлежащей параболе, согласно геометрическому определению (свойству директории) параболы, мы имеем. Поскольку, получаем уравнение параболы в координатной форме:
Обратите внимание, что в полярных координатах уравнения эллипса, гиперболы и параболы совпадают, но описывают разные линии, так как они отличаются эксцентриситетом (для эллипса, для параболы, для гиперболы).
Как строить параболу по квадратному уравнению
школьникам важно научиться правильно рисовать параболу по указанным параметрам.
Анализируя выражения и уравнения, вы можете увидеть следующее:
- Точка пересечения искомой линии с вектором ординат будет иметь значение, равное c.
- Все точки на графике (по оси абсцисс) будут симметричными относительно главного конца функции.
Кроме того, точки пересечения с OX можно найти, зная дискриминант (D) этой функции:
D = (b2 4 * a * c).
Для этого установите выражение равным нулю.
Наличие корней параболы зависит от результата:
- D ˃ 0, поэтому x1, 2 = (-b ± D0.5) / (2 * a),
- D = 0, поэтому x1, 2 = -b / (2 * a),
- D ˂ 0, то точек пересечения с вектором OX нет.
Получаем алгоритм построения параболы:
- определить направление ветвей,
- найти координаты вершины,
- найти пересечение с осью y,
- найти пересечение с абсциссой.
Пример 1.
Дана функция y = x2 5 * x + 4. Необходимо построить параболу. Действуем по алгоритму:
- a = 1, поэтому ветви направлены вверх,
- крайние координаты: x = (-5) / 2 = 5/2, y = (5/2) 2-5 * (5/2) + 4 = -15/4,
- пересекает ординату при значении y = 4,
- найти дискриминант: D = 25 — 16 = 9,
- в поисках корней:
- Х1 = (5 + 3) / 2 = 4, (4, 0),
- Х2 = (5-3) / 2 = 1, (1, 0).
Из полученных точек можно построить параболу.
Пример 2.
Для функции y = 3 * x2 2 * x 1 вам нужно построить параболу. Действуем по заданному алгоритму:
- a = 3, поэтому ветви направлены вверх,
- крайние координаты: x = (-2) / 2 * 3 = 1/3, y = 3 * (1/3) 2 — 2 * (1/3) — 1 = -4/3,
- ось y будет пересекаться при значении y = -1,
- найти дискриминант: D = 4 + 12 = 16. Итак, корни:
- Х1 = (2 + 4) / 6 = 1, (1.0),
- Х2 = (2-4) / 6 = -1/3, (-1/3, 0).
Из полученных точек можно построить параболу.
Гипербола
Гипербола — это прямая линия, состоящая из всех точек плоскости, модуль разности расстояний от которой до двух заданных точек 

Точки 

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составим ее уравнение: 
Уравнение (7.6) называется каноническим уравнением гиперболы.
Уравнение (7.6) показывает, что 
Поскольку уравнение включает только четные степени x и y, гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола построена по симметрии. Из уравнения (7.6) для первого квартала имеем:
График этой функции от точки A (a, 0) неограниченно идет вправо и вверх (рис. 7.7) и приближается к прямой на столько, сколько вы хотите:
Поэтому говорят, что гипербола бессимптомно приближается к прямой (7.7), и эта прямая называется асимптотой гиперболы. Из симметрии гиперболы следует, что она имеет две асимптоты
Построим гиперболу. Сначала строим так называемый главный прямоугольник гиперболы, центр которого совпадает с началом координат, а стороны 2a и 2b параллельны осям координат. Прямые, на которых лежат диагонали этого прямоугольника, являются асимптотами гиперболы. Рисуем рисунок гиперболы (рис.7.8).
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется центром, оси симметрии называются осями гиперболы. Точки 
Эксцентриситет гиперболы — это число

Фокусные лучи точки гиперболы — это отрезки прямых, которые соединяют эту точку с фокусами


Справа — ветки 
Слева — ветви
Прямой 
Как определить, куда направлены ветви параболы
Чтобы найти направление такой кривой из выражения, необходимо определить знак перед первым параметром алгебраического выражения. Если на 0, то они направлены вверх. Если наоборот — вниз.
Кривые второго порядка в высшей математике
Выяснение взаимосвязи между различными показателями экономического характера часто приводит к форме этих взаимосвязей в виде гиперболы и параболы. В этом уроке мы дадим краткую информацию обо всех кривых второго порядка.
Окружность
Определение 9.1. Круг — это геометрическое место точек, равноудаленных от данной точки — центра круга.
Если я укажу
— центр (рисунок 9.1), N (x, y) — произвольная точка окружности, а R — ее радиус, поэтому по определению можно написать
или
Найдем условия, при которых общее уравнение второй степени с двумя переменными
определяет круг. Раскладывая скобки в (9.1.1), получаем
Сравнивая (9.1.2) и (9.1.3), находим условия A = C, B = O,
, при котором общее уравнение (9.1.2) определяет окружность.
Эллипс
Определение 9.2. Эллипс — это геометрическое место точек, для которых сумма расстояний от двух фиксированных точек на плоскости, называемых фокусами, является постоянной величиной, превышающей расстояние между фокусами.
Для эллипса с фокусами на плоскости xOy (рис. 9.2
а также
… Пусть начало координат будет в середине отрезка
… Выводим уравнение эллипса.
Если точка A — произвольная точка эллипса с координатами (x, y), то
(9.2.1)
где это находится
— постоянная сумма. Потому что
они расположены симметрично относительно начала координат, поэтому имеют координаты (ñ, 0) и (-с, 0) соответственно. Используя формулу для расчета расстояния между двумя точками, находим
… Подставляем значения
а также
в (9.2.1) получаем уравнение
Мы учетверим обе части этого уравнения. Упростить и обозначить
получать
… Разделим обе части уравнения на правую часть
Уравнение (9.2.2) называется каноническим уравнением эллипса, где a — большая полуось, b — малая полуось.
Это уравнение второго порядка, поэтому эллипс является линией второго порядка. Для определения формы эллипса используется его эксцентриситет
, то есть отношение расстояния между фокусами этого эллипса к длине его большой полуоси. Поскольку с
a, то эксцентриситет каждого эллипса меньше единицы. До такой степени, что

в равенстве
Следовательно, эксцентриситет определяется соотношением осей эллипса; а соотношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше 

получаем круг.
Две линии, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии
отсюда их называют эллиптическим директором. Ведущие уравнения
Пример:
Исследуйте, какая линия определяется уравнением
Решение:
Группируя термины, содержащие одну и ту же переменную, получаем
Из второй скобки извлекаем коэффициент a 
В каждой из скобок выберите полный квадрат
или
Сделаем замену: 

Разделив обе части этого уравнения на 
Данное уравнение определяет эллипс с полуосями 
Выберем произвольным образом прямоугольную систему координат xOy на плоскости. Используя параллельный перенос, переносим оси координат в новое начало в точке 


Гипербола
Определение 9.3.1. Гипербола — это геометрическое место точек, для которых разность расстояний от двух фиксированных точек на плоскости, называемых фокусами, является постоянной величиной, меньшей, чем расстояние между фокусами, и отличной от нуля (указанная разница принимается как абсолютная величина).
Пусть M — произвольная точка гиперболы с фокусами
(рис. 9.4) сегменты
они называются фокальными лучами точки M и обозначаются
По определению гиперболы 
и с тех пор
расположены симметрично относительно начала координат, поэтому, используя формулу для расчета расстояния между двумя точками, находим 
в равенстве
найденных выражений, получаем:

Возводя обе части этого уравнения в квадрат и обозначая

или, разделив все члены уравнения на правую часть, возьмем его в виде:
Уравнение (9.3.1) — каноническое уравнение гиперболы, линии второго порядка.
Прямоугольник со сторонами 2a и 2b, расположенный симметрично вокруг осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 
Уравнение формы
определяет гиперболу, вершины которой лежат на оси Oy (рис. 9.5).
Форма гиперболы отличается эксцентриситетом 

получать
где это находится



Линии, заданные уравнениями
они называются гиперболическими руководящими принципами.
Пример:
Изобразите уравнение геометрического места точек, у которых отношение расстояний от заданной точки A (4, 0) до заданной прямой x = 1 равно 2.
Решение:
В системе координат xOy построим точку A (4, 0) и прямую x = 1. Пусть M (x, y) — произвольная точка искомого геометрического места точек. Опускаем перпендикуляр MB к этой прямой x = 1 и определяем координаты точки B. Поскольку точка B лежит на заданной прямой, ее абсцисса равна 1. Ордината точки B равна ординате точки M. Следовательно, B (1, y) (рис. 9.6) Из условия задачи 

Возводя в квадрат левую и правую части равенства и последовательно преобразуя, находим уравнение:
Полученное уравнение определяет гиперболу, для которой действительная полуось -a = 2, а мнимая 
Определим фокусы гиперболы. Для гиперболы равенство 

— очаги гиперболы. Как видите, данная точка
A (4, 0) — правый фокус гиперболы.
Эксцентриситет полученной гиперболы равен
Подставляя значения a и b в уравнения асимптот
а также
y = — получаем уравнения асимптот гиперболы:

Для построения гиперболы строим базовый прямоугольник с полуосями 
а также
а затем строим саму гиперболу (рис. 9.6).
Парабола
Определение 9.4.1. Парабола — это место точек, для каждой из которых расстояние от фиксированной точки плоскости, называемой фокусом, равно расстоянию от фиксированной линии, называемой директрисой (директриса не проходит через фокус).
Обозначим фокус параболы — F, расстояние от фокуса до направляющей — p (p> 0) (рис. 9.7). Проведите ось абсцисс через фокус F перпендикулярно направляющей. Начало координат будет посередине между фокусом и направляющей. Пусть A — произвольная точка координатной плоскости (x, y) и пусть
… Тогда точка A лежит на параболе, если r = d, где d — расстояние от точки A до директрисы. Focus F имеет координаты
.
Следовательно
И расстояние
Подставив в формулу r = d, получим
или
(9.4.1)
Уравнение (9.4.1) — каноническое уравнение параболы. Уравнения
также определите притчи.
легко доказать, что уравнение 

и делаем параллельный перенос с формулами
В новых координатах преобразованное уравнение примет вид:
где p — положительное число, определяемое равенством
Пример:
Пусть задана точка F и прямая y = -1 (рис. 9.8). Множество точек P (x, y), для которых расстояние | PF | равно расстоянию



Методы нахождения координат вершины
Очень часто при решении задач функция квадратичного типа может быть представлена в определенной форме, которую нужно привести в удобочитаемый вид с помощью математических преобразований. Последний термин означает, что необходимо преобразовать формулу параболы для удобного построения таблицы и принципиальной схемы. Это делается по следующему алгоритму для примера z = t ^ 2 + 4t + 2:
- Приравнять к нулю (квадратное уравнение): t ^ 2 + 4t + 2 = 0.
- Выполните подготовительную операцию, чтобы выделить квадрат: t ^ 2 + 4t + 2 + 2-2 = 0.
- Выберите формулу сокращенного умножения — квадрат: (t + 2) ^ 2 -2 = 0.
- Переместите «-2» вправо, то есть (t + 2) ^ 2 = 2.
- Найдите вершину на основе решения тождества без «-2″.
- Определяет ординату z: z = — (2), которая представляет собой число из правой части выражения, умноженное на -1.
- Вычислите координату фокуса (смещение от начала координат): (t; z) = (- 2; -2).
Методика позволяет найти фокус без дополнительных формул. Однако есть другой способ определить вершину, где применяется производная функции:
- Найдите производную: z ‘= 2t + 4.
- Установите z ‘равным нулю: 2t + 4 = 0.
- Найдите корень: t = -2.
- Замените исходную функцию, чтобы найти ординату, которая равна z = -2.
- Координата вершины: (-2; -2). То же, что и в предыдущем примере.
Существуют программные продукты для определения параметров блюда. Имена имеют английскую номенклатуру, то есть «притча».
Уравнение квадратичной функции имеет вид y = a * (x — x₀)2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2×2 + 3x — 5 при a = 1 второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.
Как мы строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого вам понадобятся:
- построить y = x2,
- умножьте ординаты всех точек на графике на 2,
- переместите его по оси OX на 1 единицу вправо,
- переместите его по оси OY на 4 единицы вверх.
- Нарисуйте притчу для каждого случая.
Исследование на плоскости уравнения второй степени
Рассмотрим уравнение:
(7,9)
где между коэффициентами A, B, C стоят ненулевые, то есть (7.9) является уравнением второй степени относительно x и y.
Возьмем на плоскости две прямоугольные системы координат: Oxy, которую мы назовем старой, и новую, полученную из Oxy, повернув ее на угол вокруг начала координат
Старые координаты x, y выражаются через новые координаты
из формул:
(7.10)
Подставляя выражения для x и y в уравнение (8), получаем:
(7.11)
Это уравнение в системе координат
определяет ту же линию, что и уравнение (7.9) в системе Oxy.
Если в уравнении (7.9) 

(7.12)
Преобразуя это уравнение и применяя параллельный перенос осей координат, мы приходим к уравнению:
(7.13)
В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:
Рассматривая далее методически все случаи, приходим к выводу: уравнение вида (7.9) определяет одну из следующих фигур: эллипс, гипербола, парабола, пара пересекающихся прямых, пара параллельных прямых, прямая линия, точка или пустой набор.
Геометрический смысл параметра в уравнении параболы
Поясним геометрический смысл параметра в каноническом уравнении параболы. Подставляя в уравнение (3.51), получаем, т.е.. Следовательно, параметр равен половине длины хорды параболы, проходящей через ее фокус перпендикулярно оси параболы.
Фокальный параметр параболы, а также эллипса и гиперболы составляет половину длины струны, которая проходит через ее фокус перпендикулярно фокальной оси (см. Рис. 3.45, c). Из уравнения параболы в полярных координатах получаем, что параметр параболы совпадает с ее фокальным параметром.
- Параметр параболы характеризует ее форму. Чем больше, чем шире ветви параболы, чем ближе к нулю, тем уже ветви параболы (рис. 3.46).
- Уравнение (в) определяет параболу, которая лежит слева от оси ординат (рис. 3.47, а). Это уравнение сводится к каноническому изменением направления оси абсцисс (3.37). На рис. 3.47, а показаны заданная и каноническая системы координат .
- Уравнение определяет параболу с вершиной, ось которой параллельна оси абсцисс (рис. 3.47.6). Это уравнение сводится к каноническому с помощью параллельного переноса (3.36).
Уравнение также определяет параболу с вершиной, ось которой параллельна оси ординат (рис. 3.47, c). Это уравнение сводится к каноническому за счет параллельного переноса (3.36) и переименования осей координат (3.38). На рис. 3.47, б, в показаны заданные системы координат и канонические системы координат .
- График квадратного трехчлена представляет собой параболу с вершиной в точке, ось которой параллельна оси ординат, ветви параболы направлены вверх (в) или вниз (в). Фактически, выделив полный квадрат, мы получим уравнение
что сводится к канонической форме, где, используя замену и .
Знак выбирается так, чтобы он совпадал со знаком основного коэффициента. Эта замена соответствует композиции: параллельный перенос (3.36) с помощью и, переименование осей координат (3.38), а в случае изменения направления оси координат (3.37). На рис. 3.48, а, б показаны указанные системы координат и канонические системы координат для случаев и соответственно.
- Ось абсцисс канонической системы координат является осью симметрии параболы, поскольку изменение переменной на не меняет уравнение (3.51). Другими словами, координаты точки, принадлежащей параболе, и координаты точки, симметричной точке относительно оси абсцисс, удовлетворяют уравнению (3.S1). Оси канонической системы координат называются главными осями параболы.
Пример 3.22. Нарисуйте параболу в канонической системе координат. Найдите параметр фокуса, координаты фокуса и уравнение направляющей.
Решение. Строим параболу с учетом ее симметрии относительно оси абсцисс (рис. 3.49). При необходимости определяем координаты некоторых точек параболы. Например, подставив параболы в уравнение, мы получим. Следовательно, точки с координатами принадлежат параболе.
Сравнивая данное уравнение с каноническим (3.S1), определяем фокальный параметр:. Координаты фокуса, например… Составим уравнение директрисы, т.е.
Пример решения
Для практического применения теоретических знаний о параболе рекомендуется решать задачи. Условие одного из них формулируется следующим образом: дана формула функции параболы f = (t + 2) ^ 2 -3t ^ 2 + 8t-5 + 3 (t-1) ^ 2, для которой необходимо подготовить данные для построения графика в схематическом виде (8 значений). Ее следует решать по следующей методике:
- Раскройте скобки и приведите аналогичные элементы: f = t ^ + 4t-1.
- Равно 0: t ^ 2 + 4t-1 = 0.
- Выберите квадрат: (t + 2) ^ 2-5.
- Прямая передача: (t + 2) ^ 2 = 5.
- Вершина с координатами: (-2; -5).
- Вычислите нули функции с абсциссами: t ^ 2 + 4t-1 = 0. Корни: t1 = -2- (5) ^ 0,5 и t2 = -2 + (5) ^ 0,5. Координаты: (-2- (5) ^ 0,5,0) и (-2+ (5) ^ 0,5,0)
- Нули функции (пересечение ординаты при t = 0): (0 + 2) ^ 2-5 = -1. Координата — (0; -1).
- Строим стол.
| ж | -5 | -3 | -1 | 0 | -5 | 0 | -1 | -3 | -5 |
| т | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
Вы можете приступить к построению диаграммы. Специалисты советуют нарисовать его карандашом. Отметить нужно только точки, указанные в таблице. Кроме того, необходимо указать нули функции на графике, а также ее пересечения с ординатой. Ветви искомой параболы будут направлены вверх, поскольку квадрат коэффициента 1> 0.
Таким образом, парабола — это кривая 11 порядка, которая используется для описания некоторых физических явлений, траекторий тел в пространстве, а также для описания квадратичной связи между двумя величинами.
Каноническое уравнение параболы
На рисунке показана прямоугольная система координат (XOY), одна крайность, направление рисования ветвей функции по оси абсцисс.
Каноническое уравнение:
у2 = 2 * р * х,
где коэффициент p — фокальный параметр параболы (AF).
В алгебре это будет записано иначе:
y = a x2 + bx + c (узнаваемый образец: y = x2).
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .
Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .
Если a = 0 , функция принимает вид y = b .
Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.



Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.
Функция вида y=ax2+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Рисунок №1.
Вершина параболы. Формула.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
х0=−b2a
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax2+bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0=−b2a=82∙2=84=2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2∙22 – 8∙2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Ответ: (2; –3).
Нули параболы
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
х2 +4х – 5=0
а=1, b=4, с= –5
D=b2 – 4ac=42 – 4∙1∙(−5)=36
x=−b±√D2a
x=−4±√362; х1=–5; х2=1
Значит, нули функции равны –5 и 1
Ответ: –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Ответ: 231
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
х0=−b2a=−42∙2=−44=−1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
Ответ: 231
Задание 11OM21R
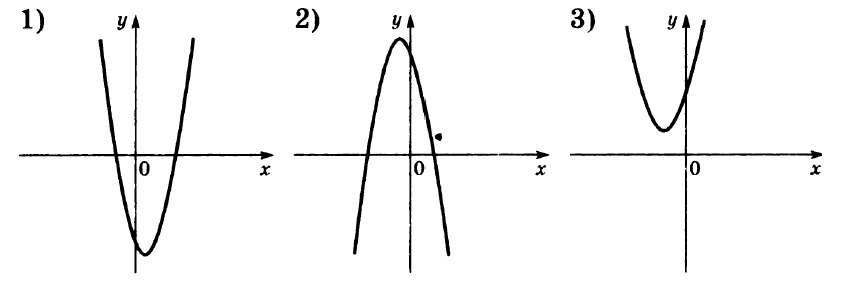
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор
Задание OM1101o
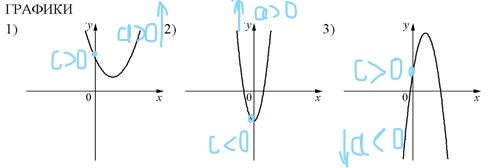
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 10.8k