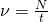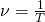Загрузить PDF
Загрузить PDF
Количество оборотов в минуту – это мера скорости вращения предмета. Информация о частоте вращения предмета помогает определить скорость ветра, передаточное число, мощность двигателя, а также скорость вылета и глубину прохождения пули[1]
. Существует несколько способов подсчета частоты вращения, в зависимости от того, в каких целях будет использоваться полученное значение. Мы рассмотрим самые простые из них.
-
1
Выберите часть вращающегося предмета, за которой удобно следить. Такой способ лучше всего подходит для предметов с длинными рычагами или рукоятками. В качестве примера можно привести анемометр (устройство для измерения скорости ветра) или ветровую турбину. Выберите рукоятку или лопасть и сосредоточьтесь на ней.
- Можно выделить нужную вам лопасть или рукоятку, например, привязав к ней цветную нить или нанеся полосу краски.
-
2
Возьмите хронометр. Вам нужно будет засечь время. С этим отлично справится секундомер или хронометр на смартфоне или планшете.
-
3
Запустите секундомер.
-
4
Начните считать количество оборотов выделенной вами лопасти или рукоятки. Полный оборот происходит тогда, когда лопасть возвращается в исходное положение.
-
5
Прекратите подсчет по истечении 1 минуты. Так вы узнаете частоту вращения – количество оборотов предмета в минуту.
- Можно не прекращать подсчет через 1 минуту, а продолжать 2-3 минуты и потом разделить полученное значение на количество истекших минут (это удобно для медленно вращающихся предметов). Так вы исключите из подсчета частичное вращение, если предмет не успел вернуться в исходное положение к завершению 1 минуты.
- Если предмет вращается быстро, то можно подсчитать обороты за 15 секунд и потом умножить результат на 4.[2]
- Можно соотнести частоту вращаемого ветром объекта с фактической скоростью ветра, сначала узнав длину окружности, которую проходит одна из вращающихся лопастей. Затем данную величину нужно преобразовать в мили или километры и умножить на частоту вращения, узнав, таким образом, какое расстояние преодолевает предмет за минуту вращения. Умножив это число на 60, вы определите расстояние, преодолеваемое за 1 час, что и будет скоростью ветра.[3]
Реклама
-
1
Подсчитайте количество зубьев ведущего колеса. Ведущее зубчатое колесо – это шестеренка, которая соединена с двигателем или другим источником питания посредством оси. Скорость вращения ведущего ЗК обычно известна.
- В целях данного примера мы допустим, что ЗК имеет 80 зубьев и скорость вращения 100 об/мин.
-
2
Подсчитайте количество зубьев ведомого колеса. Ведомое ЗК – это шестеренка, зубья которой зацепляются с зубьями ведущего ЗК. Зубья ведущего ЗК толкают зубья ведомого ЗК, что приводит к вращению всей ведомой шестерни. Это именно та шестерня, скорость вращения которой мы будем подсчитывать.
- В целях данного примера мы возьмем два ведомых ЗК различной величины, одно из которых меньше ведущей шестерни, а второе – больше.
- Меньшее ведомое ЗК имеет меньше зубьев по сравнению с ведущей шестерней. Количество зубьев меньшей шестерни – 20.
- Большее ведомое ЗК имеет больше зубьев по сравнению с ведущей шестерней. Количество зубьев большей шестерни – 160.
-
3
Найдите соотношение ведущей и ведомой шестерни. Чтобы узнать соотношение двух шестерней, вам нужно разделить количество зубьев одной шестерни на количество зубьев другой. Хотя правильным способом будет разделить количество зубьев ведущей шестерни на количество зубьев ведомой шестерни или наоборот, мы разделим большее количество на меньшее.
- Для меньшей ведомой шестерни мы разделим количество зубьев ведущей шестерни (80) на 20 и получим 80 / 20 = 4.
- Для большей ведомой шестерни мы разделим количество ее зубьев (160) на количество зубьев ведущей шестерни (80) и получим 160 / 80 = 2.
-
4
Частота вращения ведомой шестерни. Способ подсчета будет зависеть от размера ведомой шестерни относительно ведущего ЗК.
- Если ведомая шестерня меньше ведущей, то мы умножаем результат отношения ведущей и ведомой шестерни на частоту вращения ведущего ЗК. Для меньшей шестерни с 20 зубьями мы умножим частоту вращения ведущего ЗК (100) на 4 (см. предыдущий шаг) и получим 100 x 4 = 400 об/мин для ведомой шестерни.
- Если ведомая шестерня больше ведущей, то мы разделим частоту вращения ведущей шестерни на результат отношения ведомой и ведущей шестерни. Для большей шестерни со 160 зубьями мы разделим частоту вращения ведущей шестерни (100) на 2 (см. предыдущий шаг) и получим 100 / 2 = 50 об/мин для ведомой шестерни.[4]
Реклама
-
1
Определите начальную скорость пули. Начальная или дульная скорость – это скорость прохождения пули через оружейный ствол в момент выстрела. Эта величина обычно измеряется в метрах в секунду (м/с).
- В целях данного примера мы допустим, что начальная скорость составляет 610 м/с.
-
2
Определите скорость вращения в стволе. Внутри оружейного ствола имеются винтовые канавки или нарезы, которые придают пуле вращение. Вращение помогает стабилизировать полет пули после вылета из ствола и на пути в цели. Скорость вращения указывается как отношение 1 оборота к длине в миллиметрах.[5]
- В целях данного примера мы допустим, что скорость вращения составляет 1:254 мм.
- Чем меньше скорость вращения, тем больше вращения будет придаваться пуле нарезом внутри ствола. Слишком высокое вращение может привести к разрыву пули или снижению точности на ближней дистанции.[6]
-
3
Начальная скорость и скорость вращения должны быть выражены в одинаковых единицах в секунду. Стандартными единицами измерения являются футы и дюймы или метрические единицы длины.[7]
- Если скорость вращения указана как 1 на длину в дюймах, а начальная скорость указана в футах за секунду, то начальную скорость нужно умножить на 12, чтобы перевести ее в дюймы за секунду.
- В нашем примере начальная скорость 2000 футов в секунду, умноженная на 12, дает 2000 x 12 = 24000 дюймов в секунду.
- Если скорость вращения указана как 1 на длину в миллиметрах, а начальная скорость указана в метрах за секунду (м/с), то начальную скорость нужно умножить на 1000, чтобы перевести ее в миллиметры за секунду (мм/с).
- Метрическое выражение 610 м/с умножаем на 1000 и получаем 610 x 1000 = 610000 мм/с.
-
4
Разделите полученный результат на длину скорости вращения. Так мы получим вращение, выраженное в оборотах за секунду.[8]
- Разделив начальную скорость 24000 дюймов в секунду на длину в 10 дюймов мы получим 24000 / 10 = 2400 оборотов в секунду.
- Разделив начальную скорость 610000 мм/с на длину в 254 мм мы получим 610000 / 254 = 2400 оборотов в секунду (как и ожидалось, результаты получились одинаковыми как для футов с дюймами, так и для эквивалентных выражений в метрических единицах).
-
5
Умножаем на 60. В минуте 60 секунд, поэтому за минуту пуля сделает в 60 раз больше оборотов, чем за секунду.[9]
- Умножив 2400 оборотов в секунду на 60 мы получим 2400 x 60 = 144000 об/мин.
Реклама
Советы
- В разных языках количество оборотов в минуту выражается разными сокращениями. Так, в английском языке это будет «RPM» (revolutions per minute), во французском «tr/mn» (tours par minute), а в немецком «U/min» (Umdrehungen por Minute).[10]
Реклама
Предупреждения
- Обратите внимание, что при визуальном наблюдении и расчете частоты вращения пули во внимание не принимается трение.[11]
[12]
Реклама
Что вам понадобится
- Анемометр, ветровая турбина или вентилятор (для визуальных наблюдений)
- Хронометр (для визуальных наблюдений)
- Краска или цветная нить (для визуальных наблюдений, чтобы отменить одну рукоятку или лопасть)
Об этой статье
Эту страницу просматривали 13 414 раз.
Была ли эта статья полезной?
|
0 / 0 / 0 Регистрация: 20.05.2018 Сообщений: 73 |
|
|
1 |
|
Определить начальную частоту вращения второго диска13.10.2019, 14:13. Показов 2753. Ответов 1
В момент начальный времени первый диск имел частоту вращения n1 = 60 об/мин, ε = 2п/T = 2пv; v= N/t; не могу понять как связать всё в одно уравнение, чтобы найти из этого уравнение n2. Заранее спасибо.
0 |
|
572 / 361 / 186 Регистрация: 11.01.2019 Сообщений: 1,220 |
|
|
13.10.2019, 20:30 |
2 |
|
Решение Пишем два уравнения (частоту вращения об/мин пересчитываем в рад/с, ускорение считаем в рад/с2) Из 1-го уравнения находим t=6.28 с, из 2-го — начальную частоту второго диска n20 =10*6.28 1/с=600 об/мин.
1 |
Сообщение было отмечено Фуфлыжник как решение
Скачать материал
Скачать материал
- Сейчас обучается 268 человек из 65 регионов
Описание презентации по отдельным слайдам:
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
17 слайд
1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
Дано:
I = 245 кг·м2
= 20 об/c
t = 1 минMтр — ?
N — ?
Решение
Запишем уравнение основного закона динамики вращательного движения:
В проекциях на ось OX:
Отсюда проекция вектора углового ускорения на ось OX:
Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Проекция угловой скорости колеса на ось OX: -
18 слайд
Колесо остановится, поэтому
Решение (продолжение)
Величина (модуль) вектора углового ускорения:
1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
Для модулей векторов: -
19 слайд
Величина углового перемещения колеса изменяется как
Решение (продолжение)
Из двух кинематических уравнений движения получаем систему уравнений:
Величину углового ускорения ε получим из второго уравнения и подставим в первое:
1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. -
20 слайд
1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
Решение (продолжение)
Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения:
После подстановки получим:
Отсюда полное число оборотов колеса до остановки:
Ответ: Мтр = 513 H·м, N = 600. -
21 слайд
5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Дано:
I = 245 кг·м2
= 20 об/c
N = 1000Mтр — ?
t — ?
Решение
Запишем уравнение основного закона динамики вращательного движения:
В проекциях на ось OX:
Отсюда проекция вектора углового ускорения на ось OX:
Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Угловое перемещение колеса -
22 слайд
5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Величина угловой скорости колеса изменяется как
Колесо остановится, поэтому
Решение (продолжение)
Из двух кинематических уравнений движения получаем систему уравнений:
Величину углового ускорения ε получим из второго уравнения и подставим в первое: -
23 слайд
5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения:
Решение (продолжение)
После подстановки получим:
Откуда время движения до остановки: -
24 слайд
5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Решение (продолжение)
Теперь вернёмся к динамическому уравнению движения и найдём величину момента сил трения. Для проекций на ось OX:
Величина момента сил трения
Или, для краткости,
Как было получено ранее,
Теперь -
25 слайд
5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Решение (продолжение)
Ответ: t = 100 c; Мтр = 308 H·м. -
26 слайд
2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Дано:
m = 0,5 кг
I = 0,1 кг·м2
R = 20 cм
h0 = 1 мt — ?
Ек — ?
Т — ?
Решение
Прежде всего, запишем динамическое уравнение движения груза. Из второго закона Ньютона:
Для проекций на ось OY:
Если учесть, что груз опускается, то
где a — величина (модуль) проекции ускорения на ось OY.
a = const., начальная скорость груза равна нулю, следовательно кинематическое уравнение движения можно записать так: -
27 слайд
2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Решение (продолжение)
Через время t груз окажется на земле (y = 0), поэтому
Величину ускорения можно определить из уравнения второго закона Ньютона
но для этого нужно знать величину силы натяжения нити T.
Запишем уравнение основного закона динамики вращательного движения для барабана:
В проекциях на ось OZ, перпендикулярную плоскости рисунка:
Из третьего закона Ньютона -
28 слайд
2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Решение (продолжение)
Величину углового ускорения ε можно выразить через величину линейного ускорения a:
Теперь можно записать систему уравнений, из которой можно определить a и T: -
29 слайд
2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Решение (продолжение)
Найдём величину линейного ускорения a:
Подставим выражение для a в формулу для времени движения груза: -
30 слайд
2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Ответ: t = 1,1 c; Ek = 0,82 Дж; Т = 4,1 H.
Решение (продолжение)
Кинетическая энергия груза
Скорость груза
где -
31 слайд
3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что блок вращается с угловым ускорением = 2,36 рад/c2. Блок считать однородным диском.
Дано:
Mтр = 98,1 Н·м
I = 50 кг·м2
R = 20 cм
e = 2,36 рад/c2Т2 – Т1 — ?
Решение
Вращательное движение блока описывается основным законом динамики вращательного движения.
Запишем для блока:
Для проекций на ось OZ, направленную перпендикулярно плоскости рисунка.
Согласно третьему закону Ньютона -
32 слайд
3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т1 – Т2 по обе стороны блока, если известно, что блок вращается с угловым ускорением = 2,36 рад/c2. Блок считать однородным диском.
Решение (продолжение)
Из этого уравнения получаем:
Ответ: T2 – T21 =1,08 кН. -
33 слайд
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
Дано:
Mтр = 98,1 Н·м
I = 50 кг·м2
R = 20 cм
m1 = 1 кг
m2 = 1,5 кгТ2 – Т1 — ?
Решение
Поступательное движение гирь описывается вторым законом Ньютона, а вращательное движение блока – основным законом динамики вращательного движения.
Запишем для гирь и блока:
Перепишем систему уравнений. Для этого первое и второе уравнения запишем для проекций на вертикальную ось OY, а третье – для проекций на ось OZ, направленную перпендикулярно плоскости рисунка. -
34 слайд
Решение (продолжение)
Согласно третьему закону Ньютона
Величину углового ускорения ε можно выразить через величину линейного ускорения a:
Нить нерастяжима, поэтому
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском. -
35 слайд
Решение (продолжение)
Система уравнений приобретает вид:
Вычтем из второго уравнения первое и выполним элементарные преобразования в третьем:
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском. -
36 слайд
Решение (продолжение)
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
Разделим первое уравнение на второе: -
37 слайд
Решение (продолжение)
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском. -
38 слайд
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение
Дано:
h = 0,5 м
0 = 0v — ?
Задачу решим с помощью закона сохранения энергии. Любое из трёх перечисленных в условии тел участвует в двух движениях – поступательном с скоростью v и вращательном вокруг своего центра масс. Поэтому кинетическая энергия тела складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения.
В системе действуют только консервативные силы (трения нет), поэтому изменение полной механической энергии равно нулю. -
39 слайд
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение (продолжение)
потенциальная энергия тела в поле силы тяжести уменьшилась.
кинетическая энергия поступательного движения тела увеличилась.
кинетическая энергия вращательного движения тела увеличилась. Здесь ω — угловая скорость вращения тела. -
40 слайд
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение (продолжение)
Любое из тел катится без проскальзывания, поэтому
По этой общей формуле можно найти скорость любого из трёх тел, для этого достаточно подставить выражение для момента инерции соответствующего тела. -
41 слайд
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение (продолжение)
1. Шар:
2. Диск: -
42 слайд
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Ответ: 1 = 2,65 м/c, 2 = 2,56 м/c, 3 = 2,21 м/c; = 3,13 м/c.
Решение (продолжение)
3. Обруч:
4. Для тела, соскальзывающего без вращения по наклонной плоскости -
43 слайд
6. Маховое колесо начинает вращаться с угловым ускорением = 0,5 рад/c2 и через время t1 = 15 с после начала движения приобретает момент импульса L1 = 73,5 кгм2/c. Найти кинетическую энергию T колеса через время t2 = 20 с после начала движения.
Решение
Дано:
= 0,5 рад/c2
ω0 = 0
t1 = 15 с
t2 = 20 с
L1 = 73,5 кгм2/cТ — ?
Кинетическую энергию вращающегося колеса можно найти как
где I – момент инерции колеса, ω2 – угловая скорость колеса в момент времени t2.
Колесо вращается равноускоренно, начальная угловая скорость вращения равна нулю.
Величина (модуль) момента импульса колеса
Отсюда -
44 слайд
6. Маховое колесо начинает вращаться с угловым ускорением = 0,5 рад/c2 и через время t1 = 15 с после начала движения приобретает момент импульса L1 = 73,5 кгм2/c. Найти кинетическую энергию T колеса через время t2 = 20 с после начала движения.
Ответ: T=490 Дж.
Решение (продолжение)
Подставим в формулу для кинетической энергии полученные выражения для момента инерции и угловой скорости. -
45 слайд
7. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы?
Решение
Дано:
m = 5 кг
ω0 = 0
t = 5 с
F = 19,6 НТ — ?
Кинетическую энергию вращающегося диска можно найти как
где I – момент инерции диска, ω – угловая скорость колеса в момент времени t.
Сила F создаёт постоянный вращающий момент, что приводит к равноускоренному вращению диска. Основной закон динамики вращательного движения можно записать так:
Для проекций на ось OX (см. рисунок):
Диск вращается равноускоренно, начальная угловая скорость вращения равна нулю, -
46 слайд
7. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы?
Ответ: T=1,92 кДж.
Решение (продолжение)
Момент инерции диска относительно данной оси вращения -
47 слайд
8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Дано:
l = 85 смv — ?
Решение
Если мы сообщим нижнему концу стержня некоторую скорость, он сможет совершить полный оборот вокруг оси, проходящей через точку О.
Если эта скорость минимальная из всех возможных, при которых стержень совершит оборот, то в верхней точке скорость стержня будет очень близка к нулю (рис. 2).
Для определения минимальной скорости, при которой возможен полный оборот стержня применим закон сохранения энергии. Трение в системе отсутствует, поэтому можно считать, что все силы, действующие в системе консервативны.
Изменение потенциальной энергии в поле сил тяжести определим по изменению положения центра тяжести стержня, который совпадает с его геометрическим центром. -
48 слайд
8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Решение (продолжение)
Потенциальная энергия стержня в поле сил тяжести увеличилась.
Кинетическая энергия стержня уменьшилась, так как в верхней точке он практически остановился.
Здесь ω — начальная угловая скорость стержня.
Момент инерции стержня относительно точки O -
49 слайд
8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Ответ: =7,1 м/c.
Решение (продолжение) -
50 слайд
9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет.
Решение
Дано:
m = 100 кг
m0 = 60 кг
n1 = 10 об/минn2 — ?
На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ:
В случае, когда человек стоит на краю платформы, момент инерции системы -
51 слайд
9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет.
В случае, когда человек стоит в центре платформы, его момент инерции относительно рассматриваемой оси равен нулю, а момент инерции системы
Решение (продолжение)
Подставим выражения для моментов инерции в закон сохранения момента импульса:
Угловая скорость связана с частотой вращения соотношением: -
52 слайд
9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет.
Ответ: 2 = 22 об/мин.
Решение (продолжение) -
53 слайд
10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1 = 2,94 кг·м2 до I2 = 0,98 кгм2? Считать платформу однородным диском. Трения нет.
Решение
Дано:
m = 80 кг
R = 1 м
1 = 20 об/мин
I1=2,94 кгм2
I2=0,98 кгм2n2 — ?
На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ:
Угловая скорость связана с частотой вращения соотношением: -
54 слайд
10. Горизонтальная платформа массой m=80 кг и радиусом R=1 м вращается с частотой 1=20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1=2,94 кгм2 до I2=0,98 кгм2? Считать платформу однородным диском. Трения нет.
Решение (продолжение)
Частота вращения после изменения момента инерции
Момент инерции системы
Момент инерции диска -
55 слайд
10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1 = 2,94 кг·м2 до I2 = 0,98 кгм2? Считать платформу однородным диском. Трения нет.
Ответ: 2=21 об/мин.
Решение (продолжение) -
56 слайд
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
Решение
Дано:
m0 = 60 кг
m = 100 кг
0 = 4 км/ч
R = 10 мn — ?
На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
В лабораторной системе отсчёта
— момент импульса системы до начала движения человека;
— момент импульса системы после начала движения человека.
В лабораторной системе отсчёта
— момент импульса платформы;
— момент импульса человека. -
57 слайд
Решение (продолжение)
Направлены моменты импульса человека и платформы в противоположные стороны. Для проекций на вертикальную ось OZ:
В уравнение входит величина проекции скорости человека в лабораторной системе отсчёта, а в условии дана скорость относительно платформы. Найдём величину скорости в лабораторноё системе отсчёта.
Как только человек начнёт движение, платформа начнёт вращаться в противоположном направлении (см. рисунок). Поэтому по закону сложения скоростей
Величина линейной скорости края платформы
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет. -
58 слайд
Решение (продолжение)
Величина линейной скорости человека в лабораторной системе отсчёта
Подставим выражение для величины линейной скорости человека в лабораторной системе отсчёта в уравнение закона сохранения момента импульса:
Теперь осталось определить угловую скорость вращения платформы из последнего уравнения.
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет. -
59 слайд
Решение (продолжение)
Напомним, что I – момент инерции платформы, которая имеет форму диска.
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет. -
60 слайд
Ответ: = 3,6 об/мин.
Решение (продолжение)
Угловая скорость связана с частотой вращения соотношением:
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 264 641 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 04.12.2020
- 171
- 0
- 19.11.2020
- 576
- 0
- 10.11.2020
- 795
- 15
- 24.10.2020
- 1914
- 31
- 15.10.2020
- 162
- 1
- 15.08.2020
- 115
- 0
- 03.07.2020
- 2334
- 34
- 26.04.2020
- 929
- 7
Вам будут интересны эти курсы:
-
Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
-
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
-
Курс повышения квалификации «Введение в сетевые технологии»
-
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
-
Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс повышения квалификации «Организация маркетинга в туризме»
-
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
Как найти частоту вращения
Измерение частоты вращения различных механизмов производится при помощи тахометров, тахогенераторов с вольтметрами, частотомеров, стробоскопов и измерителей линейной скорости. Первый из этих приборов позволяет получать результат непосредственно, остальные — после несложного пересчета показаний.
Случается так, что механизм оборудован датчиком частоты вращения, но подходящего тахометра нет, зато имеется частотомер. Произвести измерение можно и в этом случае. Подайте на датчик внешнее питание, а вместо тахометра подключите частотомер. Частоту вращения вычислите по следующей формуле:ω=(f*60)/n, где ω — частота вращения, об/мин, f — показания частотомера, Гц, n — количество импульсов, вырабатываемых датчиком за один оборот.
Если механизм оборудован тахогенератором либо допускает его установку, частоту вращения измеряйте так. Если тахогенератор еще не установлен, установите его при остановленном механизме. К тахогенератору подключите вольтметр и, если это необходимо, источник напряжения возбуждения. Запустите механизм и после выхода его на рабочий режим измерьте напряжение, вырабатываемое тахогенератором. Пересчитайте его в частоту вращения, руководствуясь графиком или формулой из инструкции к тахогенератору.
Измерение частоты вращения стробоскопом осуществляют бесконтактным способом. При остановленном механизме нанесите на ту его деталь, частоту вращения которой необходимо измерить, фломастером метку. Запустите механизм и дайте ему раскрутиться. Направьте стробоскоп на вращающуюся деталь, после чего регулятором частоты вспышек добейтесь, чтобы метка казалась неподвижной. Шкала регулятора у стробоскопа обычно имеет градуировку с импульсах в минуту — в этом случае пересчет не потребуется. Если же она имеет градуировку в герцах, умножьте показания на 60.
Измеритель линейной скорости имеет резиновый ролик, который прижимают к гладкой поверхности вращающегося вала. Прижатие ролика к поверхностям, не являющимся гладкими, недопустимо. Измерив линейную скорость, пересчитайте ее в частоту вращения по формуле:ω=(v*60)/(π*(D/1000)), где ω — частота вращения, об/мин, v — измеренная линейная скорость, м/с, D — диаметр вала, мм
Если измеряется частота вращения одного звена механизма, а найти необходимо частоту вращения другого звена, связанного с ним через передачу того или иного рода, пересчет осуществляют, руководствуясь передаточным отношением этой передачи.
Частоту вращения некоторых механизмов можно найти, не прибегая к использованию каких-либо дополнительных приборов, поскольку все необходимое для этого уже имеется в устройстве, частью которого является механизм. Так, если таходатчик компьютерного вентилятора присоединен к материнской плате компьютера, определить частоту его вращения можно, войдя в режим CMOS Setup и выбрав в меню пункт PC Health Status. В транспортном средстве, оборудованном тахометром, можно без каких-либо дополнительных приспособлений в любой момент узнать частоту вращения коленчатого вала двигателя.
Переход от угловой к линейной скорости
Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:
ν = 2*π*R / Т = 2*π*R* ν.
Так как ω = 2*π*ν, то получается:
Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.
К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.
Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:
а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.
Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.
Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.
Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.
Частота дискретных событий, частота вращения
Определение Частотой дискретных колебаний
($n$) — называют физическую величину, которая равна количеству действий (событий) в единицу времени.
Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(7right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(8right).]
Синхронные и асинхронные электромашины
Двигатели переменного напряжения есть трёх типов: синхронные, угловая скорость ротора которых совпадает с угловой частотой магнитного поля статора; асинхронные – в них вращение ротора отстаёт от вращения поля; коллекторные, конструкция и принцип действия которых аналогичны двигателям постоянного напряжения.
Синхронная скорость
Скорость вращения электромашины переменного тока зависит от угловой частоты магнитного поля статора. Эта скорость называется синхронной. В синхронных двигателях вал вращается с той же быстротой, что является преимуществом этих электромашин.
Для этого в роторе машин большой мощности есть обмотка, на которую подаётся постоянное напряжение, создающее магнитное поле. В устройствах малой мощности в ротор вставлены постоянные магниты, или есть явно выраженные полюса.
Скольжение
В асинхронных машинах число оборотов вала меньше синхронной угловой частоты. Эта разница называется скольжение «S». Благодаря скольжению в роторе наводится электрический ток, и вал вращается. Чем больше S, тем выше вращающий момент и меньше скорость. Однако при превышении скольжения выше определённой величины электродвигатель останавливается, начинает перегреваться и может выйти из строя. Частота вращения таких устройств рассчитывается по формуле на рисунке ниже, где:
- n – число оборотов в минуту,
- f – частота сети,
- p – число пар полюсов,
- s – скольжение.
Формула расчёта скорости асинхронного двигателя
Такие устройства есть двух типов:
- С короткозамкнутым ротором. Обмотка в нём отливается из алюминия в процессе изготовления;
- С фазным ротором. Обмотки выполнены из провода и подключаются к дополнительным сопротивлениям.
Регулировка частоты вращения
В процессе работы появляется необходимость регулировки числа оборотов электрических машин. Она осуществляется тремя способами:
- Увеличение добавочного сопротивления в цепи ротора электродвигателей с фазным ротором. При необходимости сильно понизить обороты допускается подключение не трёх, а двух сопротивлений;
- Подключение дополнительных сопротивлений в цепи статора. Применяется для запуска электрических машин большой мощности и для регулировки скорости маленьких электродвигателей. Например, число оборотов настольного вентилятора можно уменьшить, включив последовательно с ним лампу накаливания или конденсатор. Такой же результат даёт уменьшение питающего напряжения;
- Изменение частоты сети. Подходит для синхронных и асинхронных двигателей.
Внимание! Скорость вращения коллекторных электродвигателей, работающих от сети переменного тока, не зависит от частоты сети.
Способы определения характеристик электромотора.
Чтобы определить, к какой из этих групп относится двигатель, не нужно разбирать его, как это советуют некоторые специалисты, чтобы обеспечить себе заказ на работу. Дело в том, что разбор электродвигателя может осуществить только мастер достаточной квалификации. На самом же деле достаточно открыть защитную крышку (другое название подшипниковый щит) и найти катушку обмотки. Таких катушек может быть несколько, но достаточно одной. В случае если к валу прикреплены полумуфта или шкив, потребуется снять еще и нижний щит.
Если катушки соединены при помощи деталей, которые мешают рассмотреть информацию, эти детали ни в коем случае нельзя отсоединять. Нужно попробовать определить на глаз соотношение размера катушки и статора.
Статором называется неподвижная часть электромотора, подвижная же имеет название ротор. В зависимости от конструктивных особенностей, в качестве ротора может выступать как сама катушка, так и магниты.
Если катушка закрывает собой половину кольца статора, такой двигатель относится к третьей группе, то есть способен выдавать до 3000 оборотов. Если размер катушки составляет треть от размеров кольца, это мотор второго типа, соответственно, он способен развить 1500 оборотов в минуту. Наконец, если катушка только на четверть закрывает собой кольцо, это первый тип. Электромотор развивает мощность в 1000 оборотов.
Существует еще один способ определения частоты вращения вала роторной части. Для этого также нужно снять крышку и найти верхнюю часть обмотки. По расположению секций обмотки и определяется скорость. Обычно внешняя секция занимает 12 пазов. Если сосчитать общее количество пазов и разделить на 12, можно получить число полюсов. Если число полюсов равно 2, двигатель имеет скорость вращения около 3000 об/мин. Если полюсов получилось 4, это соответствует 1500 оборотам в минуту. Если 6, то 1000 об/мин. Если 8, то 700 оборотов.
Третий способ определения количества оборотов внимательно осмотреть бирку на самом двигателе. Цифра на маркировке в конце и соответствует числу полюсов. Например, для маркировки АИР160S6 последняя цифра 6 указывает, сколько полюсов использует катушка.
Проще же всего измерить число оборотов специальным прибором тахометром. Но в силу узкой специализации применения данный способ нельзя рассматривать как общедоступный. Таким образом, даже если не сохранилось никакой технической документации, существует как минимум 4 способа определить число оборотов электрического мотора.
Частота вращения (обращения) — это физическая величина, равная количеству оборотов, которые тело совершает за единицу времени (1 секунду).
Чтобы найти частоту вращения надо количество оборотов разделить на время совершения этих оборотов:
Частота вращения – величина, обратная периоду вращения:
Частота вращения показывает, сколько оборотов совершается за 1 с.
За единицу частоты вращения в СИ принимают частоту вращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: [1/с] или [с-1] (читается: секунда в минус первой степени). Единица частоты в СИ называется Герц [Гц].
Обозначения:
T — период обращения
ν — частота обращения
N — число оборотов
t — время, за которое тело совершило N оборотов по окружности