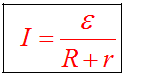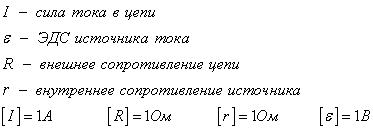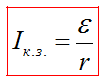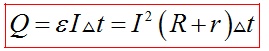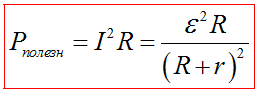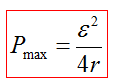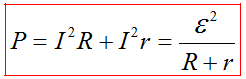III. Основы электродинамики
Тестирование онлайн
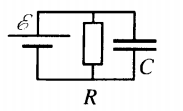
Закон Ома для замкнутой цепи
Замкнутая (полная) электрическая цепь состоит из источника тока и сопротивления.
Источник тока имеет ЭДС (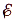
1) Напряжение на зажимах источника, а соответственно и во внешней цепи
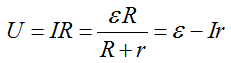
где величина 
2) Если внешнее сопротивление замкнутой цепи равно нулю, то такой режим источника тока называется коротким замыканием.
3) Для полной цепи закон Джоуля-Ленца
Коэффициент полезного действия
Мощность, выделяемая на внешнем участке цепи, называется полезной
При условии R=r мощность, выделяемая во внешней цепи, максимальная для данного источника и равна
Полная мощность — сумма полезной и теряемой мощности
Коэффициент полезного действия источника тока — отношение полезной мощности к полной
Источник ЭДС
Соединение источников тока*
Правила Кирхгофа**
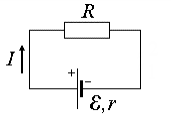
Закон Ома для замкнутой цепи.
Замкнутая
цепь содержит: источник тока, сопротивления
(потреби тока),
приборы для контроля характеристик
тока, провода, ключ. Приме может
служить цепь, приведенная на рис.5. По
отношению к источнику можно выделит
внешнюю цепь, содержащую элементы,
находящиеся данного
источника, если проследить за током от
одной его клеммы другой, и внутреннюю,
к которой относят проводящую среду
внутри источника
обозначим сопротивление внешней цепи
через R,
внутреннее
сопротивление
источника r.
Тогда
ток в цепи определяется по закону для
замкнутой цепи, который гласит, что ток
в замкнутой цепи прямо
пропорционален
величине ЭДС

внутреннего
и внешнего сопротивления цепи,
т.е.

Из
этого закона вытекают следующие частные
случаи:
• Если
R
стремится
к нулю (т.е. R
<< r),
то
ток I
стремится
к максимально
возможному
значению Iк.з
=

называемому
током короткого
замыкания.
Этот ток опасен для источников, поскольку
вызывает перегрев
источника и необратимые изменения
проводящей среды внутри него.
• Если
R
стремится
к бесконечно большой величине (т.е. при
условии, что
R
>> r),
ток I
уменьшается, и падение напряжения внутри
источника Ir
становится
намного меньше IR,
следовательно

Значит,
величину
ЭДС
источника можно практически измерить
с помощью вольтметра,
присоединенного
к клеммам источника при условии, что
сопротивление
вольтметра
RV
>> r
при
разомкнутой внешней цепи.
Распределение
энергии при работе источника постоянного
тока
Пусть
источник постоянного тока имеет ЭДС

сопротивление
r
и
замкнут на сопротивление внешней
нагрузки R.
Проанализируем
несколько величин, характеризующих
распределение энергии
при работе источника постоянного тока.
а)
Затраченная
источником мощность Р.
Работа,
совершаемая сторонними силами в замкнутой
цепи по
перемещению
заряда dq,
равна:
dA
=

Исходя
из определения, мощность, развиваемая
сторонними силами в
источнике,
равна:

Эта
мощность расходуется источником во
внешней и внутренней по отношению
к источнику частях цепи. Используя закон
Ома для замкнутой цепи,
можно затраченную мощность представить
в виде:

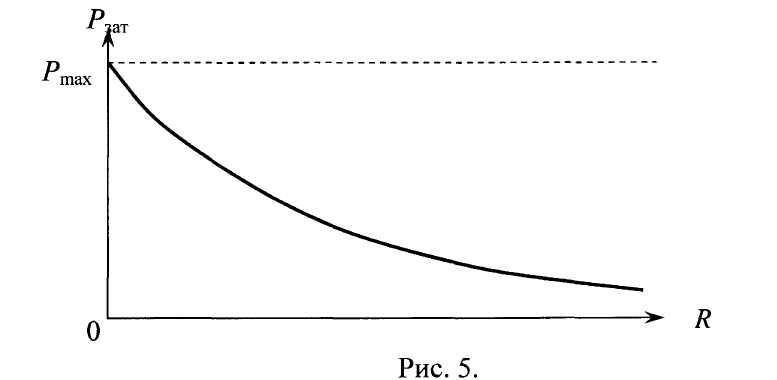
Если
сопротивление нагрузки R
уменьшается,
стремясь к нулю, то Рзат

=
Если
R
увеличивается,
стремясь в бесконечность, то Рзат
График зависимости затраченной сторонними
силами мощности Рзат
от
величины внешнего сопротивления R
показан
на рисунке 5.
б)
Полезная
мощность Рпод:_
Полезной
по отношению к источнику мощностью Рпод
считается мощность,
расходуемая источником во внешней цепи,
т.е. на внешней нагрузке.
Она равна:

Пользуясь
законом Ома для замкнутой цепи, или
заменив в последнем выражении
I
на

можно
представить в виде

Если
числитель и знаменатель этого выражения
разделить на R,
то
получится выражение

)
наглядно
демонстрирующее то, что Рпол
стремится
к нулю как при уменьшении
R
до
нуля, так и при его бесконечном увеличении,
т.к. в обоих случаях
знаменатель этого выражения стремится
к бесконечности. Это означает,
что при некотором оптимальном значении
R
полезная
мощность достигает
максимального значения
Определить
оптимальное значение R,
а
также и значение

можно,
приравняв нулю первую производную
функции Рпоя
=f(R)
пo
R:

Как
видно, полученное равенство соблюдается
при условии

из
чего следует, что R
= r.
Таким
образом, при сопротивлении внешней цепи
R,
равном
сопротивлению внутренней цепи г,
полезная
мощность источника тока
имеет максимальное значение, которое
может быть найдено по формуле:
(16)
График
зависимости Pпол=f(R)
показан
на рисунке 6.
в)
Коэффициент
полезного действия.
Величина
коэффициента полезного действия цепи
г| источника тока, в соответствии
с определением, составляет:

При
R
0
величина

величина

Рпол
стремится к нулю, и такие режимы работы
источника не представляют
практического интереса. График зависимости
КПД

тока от величины нагрузки R
показан
на рисунке 7.
Соседние файлы в папке Электричество
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
-
1 Закон Ома для полной цепи
- 1.1 Закон Ома для неоднородного участка цепи
- 2 Работа и мощность тока для полной цепи
- 3 Соединения источников тока
-
4 Правила Кирхгофа
- 4.1 Цепи с конденсаторами
Закон Ома для полной цепи
где ℰ – ЭДС источника тока (В); Аст – работа сторонних сил по перемещению заряда (Дж); q – величина перемещаемого заряда (Кл).
где I – сила тока в цепи (А); ℰ – ЭДС источника тока (В); R – внешнее сопротивление цепи (Ом); r – сопротивление источника (Ом).
При коротком замыкании сопротивление внешней части цепи стремится к нулю, т.е. R ≈ 0, тогда
где Iкз – ток короткого замыкания (А); ℰ – ЭДС источника тока (В); r – сопротивление источника (Ом).
Аккумулятор может работать в двух режимах: зарядки и разрядки. В режиме зарядки (другим источником) аккумулятор включается так, как показано на рис. 1. Ток идет в направлении, противоположном направлению тока аккумулятора, поэтому ЭДС ℰ < 0.
Рис. 1
В режиме разрядки аккумулятор включается так, как показано на рис. 2, поэтому ЭДС ℰ > 0.
Рис. 2
Закон Ома для неоднородного участка цепи
Участок цепи, на котором действуют сторонние силы, называют неоднородным (рис. 3).
Рис. 3
На неоднородном участке цепи сила тока определяется по формуле
где ℰ – ЭДС источника тока (В); φ1 – φ2 – разность потенциалов на участке цепи 1-2 (В); R1/2 = R + r – сопротивление участка 1-2 (Ом).
Знак ЭДС определяем по мнемоническому правилу: при переходе вдоль тока через источник ЭДС берется с последним знаком. Например, на рис. 3 а – ЭДС берем со знаком «+»; на рис. 3 б – со знаком «–».
Работа и мощность тока для полной цепи
Для замкнутой цепи, мощность, выделяемая на внешнем участке цепи, называется полезной мощностью. Она равна
(~P_p = I^2 cdot R) .
С учетом закона Ома для участка цепи (~I = dfrac{U}{R}) полезную мощность можно найти, если известны любые две величины из трех: I, U, R.
(~P_p = U cdot I) , (~P_p = I^2 cdot R) , (~P_p = dfrac{U^2}{R}) .
Для замкнутой цепи, мощность, выделяемая на внутреннем сопротивлении источника, называется теряемой мощностью. Она равна
(~P_t = I^2 cdot r) .
Полная мощность источника тока равна
(~P = P_p + P_t) или Р = I·ℰ ,
где Р – полная мощность источника тока (Вт); Рp – полезная мощность (Вт); Рt – теряемая мощность (Вт); I – сила тока в цепи (А); R – внешнее сопротивление (Ом); r – сопротивление источника (Ом); U – напряжение на участке (В); ℰ – ЭДС источника тока (В).
(~eta = dfrac{P_p}{P}) ,
где η – КПД источника тока; Р – полная мощность источника тока (Вт); Рp – полезная мощность (Вт).
Соединения источников тока
При соединении N источников тока с ℰ1, ℰ2, …, ℰN и сопротивлениями r1, r2, …, rN: последовательно
ℰ = ±ℰ1 ± ℰ2 ± … ± ℰN , r = r1 + r2 + … + rN ;
параллельно одноименными полюсами, если ℰ1 = ℰ2 = … = ℰN , то
ℰ = ℰ1 , (~frac{1}{r} = frac{1}{r_1} + frac{1}{r_2} + ldots + frac{1}{r_N}) .
Знак ЭДС определяем по мнемоническому правилу: при переходе вдоль тока через источник ЭДС берется с последним знаком.
Правила Кирхгофа
Для упрощения расчета разветвленных цепей, содержащих неоднородные участки, были созданы специальные правила – правила Кирхгофа:
- Алгебраическая сумма сил токов для каждого узла равна нулю:
-
(~pm I_1 pm I_2 pm ldots pm I_N = 0) .
-
Правило знаков для токов в узлах:
- если ток втекает в узел, то силу тока берем со знаком «+»,
- если ток вытекает из узла, то со знаком «–».
- Например, на рисунке 4 со знаком «+» берем I1 и I4, со знаком «–» – I2, I3 и I5. Тогда для узла А можно записать, что I1 — I2 — I3 + I4 — I5 = 0.
-
Рис. 4
-
- Алгебраическая сумма ЭДС в замкнутом контуре равна алгебраической сумме произведений сил токов и сопротивлений каждого из участков этого контура:
-
±I1·(R1 + r1) ± I2·(R2 + r2) ± … ± In·(Rn + rn) = ±ℰ1 ± ℰ2 ± … ± ℰk .
-
Правило знаков для токов в контурах:
- если направление тока совпадает с направлением обхода контура, то силу тока берем со знаком «+»,
- если направление тока не совпадает с направлением обхода контура, то силу тока берем со знаком «–».
-
Правило знаков для ЭДС в контурах:
- если направление тока источника совпадает с направлением обхода контура, то ЭДС источника берем со знаком «+»,
- если направление тока источника не совпадает с направлением обхода контура, то ЭДС источника берем со знаком «–».
-
Мнемоническое правило знаков для ЭДС в контурах:
- знак ЭДС соответствует знаку последней клеммы источника при переходе через источник по обходу контура.
- Например, на рисунке 5 выберем обходы контура по часовой стрелке.
-
Рис. 5
- Для контура ABC со знаком «+» берем I2 и I3, ℰ3, со знаком «–» берем ℰ2. Тогда
-
I2·(R2 + r2) + I3·(R3 + r3) = —ℰ2 + ℰ3 .
- Для контура ACD со знаком «+» берем ℰ1, со знаком «–» берем I1, I3 и I4, ℰ3. Тогда
-
—I1·(R1 + r1) — I3·(R3 + r3) — I4·R4 = ℰ1 — ℰ3 .
- Если учесть, что I1 = I4, то
-
—I1·(R1 + r1 + R4) — I3·(R3 + r3) = ℰ1 — ℰ3 .
- Примечание. Для каждого контура направление его обхода, определяющее знаки токов и ЭДС, выбирают произвольно. Если в результате решения задачи получают отрицательное значение тока на каком-то участке, то это значит, что ток на этом участке идет в направлении, противоположном выбранному обходу контура.
-
Цепи с конденсаторами
Для расчета цепей с конденсаторами используются следующие правила.
- Если несколько конденсаторов соединены параллельно, то
-
C = C1 + C2 + C3 + … + CN ,
-
q = q1 + q2 + q3 + … + qN .
-
- Если несколько конденсаторов соединены последовательно, то
-
(~frac{1}{C} = frac{1}{C_1} + frac{1}{C_2} + frac{1}{C_3} + ldots + frac{1}{C_N}) ,
-
q = q1 = q2 = q3 = … = qN .
-
- Если пластины нескольких конденсаторов соединены в один узел, не связанный непосредственно с источником тока, то алгебраическая сумма зарядов на этих пластинах равна нулю (закон сохранения заряда):
-
q1 + q2 + q3 + … + qN = 0 .
- Например, для цепи на рис. 6.
-
0 = —q1 + q2 + q3 .
-
Рис. 6
-
- Если на каком-либо из участков цепи A–B (рис. 7) имеется конденсатор и источник ЭДС, т.е. участок цепи неоднородный, то заряд конденсатора определяется ЭДС источника (с учетом знака) и разностью потенциалов на концах участка.
-
Рис. 7
- Например, для участка цепи на рис. 7 а (φA — φB > 0)
-
q = C·U = C·(ℰ + φA — φB) ;
- для участка цепи на рис. 7 б (φB — φA > 0)
-
q = C·U = C·(-ℰ + φB — φA) .
- Если в этом случае окажется, что U < 0 (ℰ > φB — φA) , то знаки зарядов на обкладках конденсатора будут противоположные, изображенным на рис. 7 б.
-
- После зарядки конденсатора значение тока через него равно нулю, напряжение на конденсаторе определяется законами последовательного и параллельного соединения.
- Например, для участка цепи на рис. 8
-
UR1 = UC1 = UC2 + UC3 , где UR2 = 0 , т.к. IR2 .
-
Рис. 8
Разомкнутые и замкнутые цепи
Начнем с самой простой схемы фонарика и от нее уже будет отталкиваться
Здесь мы видим три радиоэлемента: источник питания Bat, выключатель S и кругляшок с крестиком внутри, то есть лампочку. Все это вместе называется электрической цепью. Так как по цепи не бежит электрический ток, то такую цепь называют разомкнутой.
Но стоит нам щелкнуть выключатель, и у нас тут же загорится лампочка. Такая цепь уже будет называться замкнутой.
Электроэнергия и источник питания
Теперь давайте подробнее разберем нашу схему. Немного развернем ее в пространстве для удобства, игнорируя ГОСТ по обозначению источника питания:
Как мы помним с прошлой статьи, электрический ток бежит от точки с бОльшим потенциалом, то есть от плюса, к точке с мЕньшим потенциалом, то есть к минусу. Или говоря простым языком: от плюса к минусу. В настоящий момент у нас выключатель разомкнут. Можно сказать, что мы «оборвали» нашу цепь выключателем. В среде электриков и электронщиков говорят, что цепь » в обрыве». Ток не бежит, лампочка не горит.
Но вот мы ловким движением руки щелкаем выключатель и у нас цепь замыкается:
Дорога для электрического тока открыта, и он течет от плюса к минусу через лампочку накаливания, которая начинает ярко светиться.
Вроде бы все понятно, но не совсем. Кто или что заставляет светиться лампочку? Мало того, что она светит, она еще и греет!
Что самое первое появилось во Вселенной? Говорят, что время, хотя я думаю, что энергия). Энергия ниоткуда просто так не берется и никуда просто так не исчезает. Это и есть закон сохранения энергии, так что «побрейтесь» фанаты вечных двигателей).
В данном опыте у нас лампочка светит и греет. Получается, что лампочка излучает и тепловую и световую энергию. Вы ведь не забыли, что световые лучи передают энергию? В быту, например, мы используем солнечные панели, чтобы из лучиков получить электрический ток.
Странно наверное что я пишу в середине статьи не по теме, НООО прочитай про протоны.
Но теперь вопрос такой. Если лампочка излучает световую и тепловую энергию, то откуда она ее получает? Разумеется, от источника питания. Фраза «источник питания» уже говорит сама за себя. Берет энергию наша лампочка прямо от источника питания через проводкИ. Энергия, которая течет через проводочки, называется электроэнергией.
А откуда берет электроэнергию источник питания? Здесь уже есть разные способы добычи электроэнергии. Это может быть падающий поток воды, который крутит мощные лопасти вертушки, которая работает как генератор. Это могут быть химические реакции в батарейках и акумах. Это может быть даже солнечная панелька или вообще какой-нибудь элемент, типа Пельтье (элемент Пельтье), который может вырабатывать электрический ток под действием разности температур. Способов много, а эффект один. Сделать так, чтобы появилась ЭДС (Что такое).
Электрический ток и нагрузка
В дело идет Закон Ома. Как я уже писал, это самый значимый закон во всей электронике. Что такое по сути лампочка? Это вольфрамовый проводок в стеклянной колбе с вакуумом. Вольфрам — это металл, следовательно, он может через себя проводить электрический ток. Но весь прикол в том, что при определенном напряжении он раскаляется и начинает светиться. То есть отдавать энергию в пространство в виде тепла и излучения.
В холодном состоянии вольфрамовая нить обладает меньшим сопротивлением, чем в раскаленном, более чем в десять раз. Следовательно, лампочка — это просто как сопротивление для электрической цепи. В этой статье я взял лампочку, чтобы визуально показать нагрузку. Нагрузка — от слова «нагружать». Источнику питания не нравится, когда ему приходится отдавать электроэнергию. Он любит работать без нагрузки 
Теперь давайте представим все это с точки зрения гидравлики и механики.
Имеем трубу, по которой бурным поток течет вода. К трубе приделана вертушка, типа водяного колеса. Лопасти вертушки крутят вал.
Рисунок я чертил по всем догмам черчения: главный вид, и справа его разрез.
Если к валу ничего не цепляется, то поток воды бурно бежит по трубе и крутит колесо, а оно в свою очередь крутит вал. Такой режим можно назвать холостым режимом работы водяного колеса, то есть режимом без нагрузки.
Но что будет, если мы начнем использовать вращение вала себе во благо? Например, соединим с помощью муфты вал водяного колеса с валом мини-мельницы?
Думаю, многие из моих читателей сразу догадаются, что водяное колесо начнет притормаживать, так как мы его заставили работать. Крутиться со скоростью холостого хода у нашего вала уже не получится. Скорость будет меньше. То есть в нашем случае у нас на валу есть нагрузка. Что же будет происходить с потоком воды в трубе? Он будет тормозиться, так как лопасти вала не дадут водичке спокойно бежать по трубе. Поэтому, общий поток воды в трубе будет меньше, чем ДО холостого хода вала.
А если нагрузить вал, чтобы тот поднимал грузовой лифт?
Думаю, вся конструкция тут же встанет колом. То есть большая нагрузка станет непосильна для вала. А если бы мы сделали лопасти вертушки такие, чтобы они полностью перекрывали диаметр трубы, то поток жидкости вообще бы остановился.
Давайте разберем еще один пример для понимания. Все тот же самый рисунок:
Предположим, что мы прицепили к валу наждак, а электродвигатель убрали с этой конструкции. И вот мы решили что-нибудь шлифануть.
Итак, что у нас в результате получается? Если мы будем слабо давить на шлифовальный круг, то у нас круг начнет притормаживаться и уже будет крутиться с другой скоростью. Если мы сильнее будем давить на круг, то скорость вала еще больше упадет. Если же мощность нашего вала слабовата, мы можем добиться того, что при сильном давлении на круг вообще остановить вал. Тогда и точиться ничего не будет…
Давайте снова вернемся к мини-мельнице
Что будет если поток воды в трубе увеличить в несколько раз? Мельница будет крутиться так, что ее порвет нахрен! А если поток воды в трубе будет очень слабый? Разумеется, мельница будет молоть одно-два зернышка в час. Хотя, опять же, с большим потоком воды мы вполне можем поднять лифт.
Понимаете к чему я веду? Все завязано друг с другом! Давление в трубе, скорость потока жидкости и нагрузка… Все они связаны воедино.
Мощность электрического тока
Для того, чтобы это показать что к чему, мы возьмем две лампы на 12 Вольт, но разной мощности. На блоке питания выставляю также 12 Вольт и собираю все это дело по схеме, которая мелькала в начале статьи
Мой блок питания может выдать в нагрузку 150 Ватт, не парясь. Беру лампочку от мопеда и цепляю ее к блоку питания
Смотрим потребление тока. 0,71 Ампер
Высчитываем сопротивление раскаленной нити лампочки из закона Ома I=U/R, отсюда R=U/I=12/0,71=16,9 Ом.
Беру галогенную лампу от фары авто и также цепляю ее к блоку питания
Смотрим потребление. 4,42 Ампера
Аналогично высчитываем сопротивление нити лампы. R=U/I=12/4,42=2,7 Ом.
А теперь давайте посчитаем, какая лампочка больше всех Ватт «отбирает» у источника питания. Вспоминаем школьную формулу P=UI. Итак, для маленькой лампочки мощность составит P=12×0,71=8,52 Ватта. А для большой лампочки мощность будет Р=12х4,42=53 Ватта. Ого! У нас получилось, что лампочка, которая обладала меньшим сопротивлением, на самом деле очень даже прожорливая.
Итак, если кто не помнит, что такое мощность, могу напомнить. Мощность — это отношение какой-то полезной работы к времени, в течение которого эта работа совершалась. Например, надо вскопать яму определенных размеров. Вы с лопатой, а ваш друг — на экскаваторе:
Кто быстрее справится с задачей за одинаковый промежуток времени? Разумеется экскаватор. В этом случае, можно сказать, что его мощность намного больше, чем мощность человека с лопатой.
А теперь представьте, что нам надо полностью под ноль сточить эту железяку:
Подумайте вот над таким вопросом… У нас есть в запасе 5 мин и нам надо сточить железяку по-максимому. В каком случае железяка сточится быстрее всего: если прижимать ее к абразивному кругу со всей дури, прижимать слегка, либо прижимать в полсилы? Не забывайте, что у нас абразивный круг подцеплен к валу, который крутит поток воды в трубе. И да, труба у нас небольшого диаметра.
Кто ответил, что если прижимать в полсилы, то оказался прав. Железяка в этом случае сточится быстрее. Если прижимать ее со всей дури, то можно вообще остановить круг. Еще раз, что у нас такое мощность? Полезная работа, совершаемая за какой-то промежуток времени. А в нашем опыте полезная работа это и есть стачивание железяки по максималке. Также не забывайте и тот момент, что если мы будем слегка прижимать железяку, то мы будем ее стачивать пол дня. Поэтому, золотая середина — это давить железяку в полсилы.
Ну вот мы и снова переходим к электронике 
Поток воды — сила тока, давление в трубе — напряжение, давление железяки на круг — сопротивление. И что в результате мы получили? А то, что лампочка с меньшим сопротивлением обладает большей мощностью, чем лампочка с большим сопротивлением. Не трудно догадаться, если просто посмотреть на фото, но вживую эффект лучше
Но обязательно ли то, что чем меньше сопротивление, тем больше мощности выделяется на нагрузке? Конечно же нет. Во всем нужен расчет, как и в прошлом опыте, где мы стачивали железяку за определенное время.
И еще один фактор, конечно, тоже надо учитывать. Это давление в трубе. Прикиньте, точим-точим мы железяку, и вдруг давление в трубе стало повышаться. Может быть переполнилась башня, или кто-то открыл краник на полную катушку. Что станет с наждаком? Его обороты ускорятся, так как сила потока воды в трубе увеличится, а следовательно, мы еще быстрее сточим нашу железку.
Формула мощности для постоянного электрического тока
Поэтому формулы мощности в электронике имеют вот такой вид:
Отсюда A=IUt
где,
А — это полезная работа, Джоули
t — время, секунды
U — напряжение, Вольты
I — сила тока, Амперы
P — собственно сама мощность, Ватты
R — сопротивление, Омы
Как вы можете заметить, формула P=I2 R говорит нам о том, что не всегда на маленьком сопротивлении вырабатывается большая мощность и то, что мощность очень сильно зависит от силы тока. А как поднять силу тока? Добавить напряжения ;-). Закон Ома работает всегда и везде.
А из формулы P=U2/R, можно увидеть, что чем меньше сопротивление и больше напряжение в цепи, тем больше мощность будет выделяться на нагрузке. А что такое выделение мощности на нагрузке? Это может быть тепло, свет, какая-либо механическая работа и тд. Короче говоря, выработка какой-либо полезной энергии для наших нужд.
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Ее принято называть работой тока.
Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:
A=ΔqU
Но сила тока равна:
I=ΔqΔt
Выразим заряд:
Δq=IΔt
Тогда работа тока равна:
A=IUΔt
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.
Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:
A=I2RΔt=U2RΔt
Работа тока измеряется в Джоулях (Дж).
Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.
A=IUΔt=16·220·10=35200 (Дж)=35,2 (кДж)
Закон Джоуля-Ленца
В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.
Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:
Закон Джоуля—Ленца
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
Q=I2RΔt
Количество теплоты измеряется в Джоулях (Дж).
Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.
Используем закон Ома и закон Джоуля—Ленца:
Q=I2RΔt=(UR)2Δt=U2RΔt=1222=72 (Дж)
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Определение
Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).
Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:
P=AΔt
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P=IU=I2R=U2R
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P=I2R=0,32·10=0,9 (Вт)
Выразив силу тока через заряд, прошедший за единицу времени, получим:
P=qUt
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P=(εR+r)2R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
Pmax=(εr+r)2r=ε24r
Мощность тока внутренней цепи:
Pвнутр=I2r=(εR+r)2r
Полная мощность:
Pполн=I2(R+r)=ε2R+r
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P=(εR+r)2R
Применим закон Ома для полной цепи:
I=εR+r
Выразим сопротивление внешней цепи:
R=εI−r
Отсюда:
P=(εεI−r+r)2(εI−r)=I2(εI−r)=Iε−rI2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
rI2−Iε+P=0
I2−1I+0,75=0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
| Объем проводника цилиндрической формы |
V=Sl |
| Масса проводника цилиндрической формы |
m=ρV=ρSl |
| Количество теплоты и изменение температуры |
Q=cmΔT |
Конденсатор в цепи постоянного тока
Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.
Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.
Подсказки к задачам
| Электроемкость, заряд и напряжение |
C=qU |
| Напряженность и напряжение |
E=Ud |
| Энергия конденсатора |
W=q22C=CU22 |
| Количество теплоты |
Q=ΔW |
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?
Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:
I=εR+r
Применим закон Ома:
I=UR
Приравняем правые части выражений и получим:
εR+r=UR
Отсюда напряжение на конденсаторе равно:
U=εRR+r
Напряженность электрического поля равна:
E=Ud=εRd(R+r)=9·80,002(8+1)=720,018=4000 (Вм)
Задание EF17564
Ответ:
а) 5 Дж
б) 4 Дж
в) 3 Дж
г) 1 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу для нахождения количества теплоты, выделенной внутри источника тока.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 3 В.
• Внутреннее сопротивление источника тока: r = 1 Ом.
• Сила тока в цепи: I = 2 А.
• Напряжение на внешней цепи: U = 5 В.
Количество теплоты, выделенной внутри источника тока, равно:
Q=I2rt=22·1·1=4 (Дж)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17573
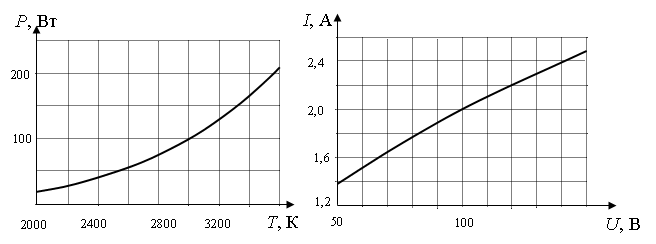
При нагревании спирали лампы накаливания протекающим по ней электрическим током основная часть подводимой энергии теряется в виде теплового излучения. На рисунке изображены графики зависимости мощности тепловых потерь лампы от температуры спирали P=P(T) и силы тока от приложенного напряжения I=I(U). При помощи этих графиков определите примерную температуру спирали лампы при силе тока I=2 A.
Ответ:
Алгоритм решения
1.Записать исходные данные.
2.С помощью графика зависимости силы тока от напряжения вычислить мощность.
3.С помощью графика зависимости мощности от температуры спирали определить ее температуру.
Решение
Нас интересует сила тока, равная 2 А. По графику зависимости силы тока от напряжения этому значение соответствует U = 100 В. Мощность определяется формулой:
P=IU=2·100=200 (Вт)
Этой мощности соответствует температура, равная около 3600 К.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17608
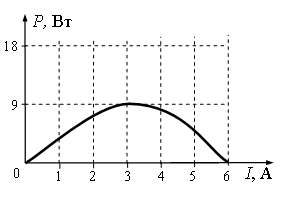
Какое из утверждений соответствует результатам опыта?
А. При коротком замыкании в цепи сила тока будет равна 6 А.
Б. При силе тока в цепи 3 А на реостате выделяется минимальная мощность.
Ответ:
а) только А
б) только Б
в) и А, и Б
г) ни А, ни Б
Алгоритм решения
- Проверить истинность каждого из утверждений.
- Выбрать верный ответ.
Решение
Согласно первому утверждению, при коротком замыкании в цепи сила тока будет равна 6 А. Это действительно так, потому что при этом значении силы тока мощность равна нулю. А это значит, что сопротивление на внешней цепи было нулевым.
Согласно второму утверждению, при силе тока в цепи 3 А на реостате выделяется минимальная мощность. Это не так. На графике этой силе тока соответствует максимальная мощность.
Верно только первое утверждение «А».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.4k