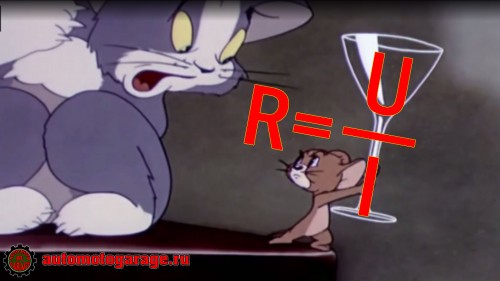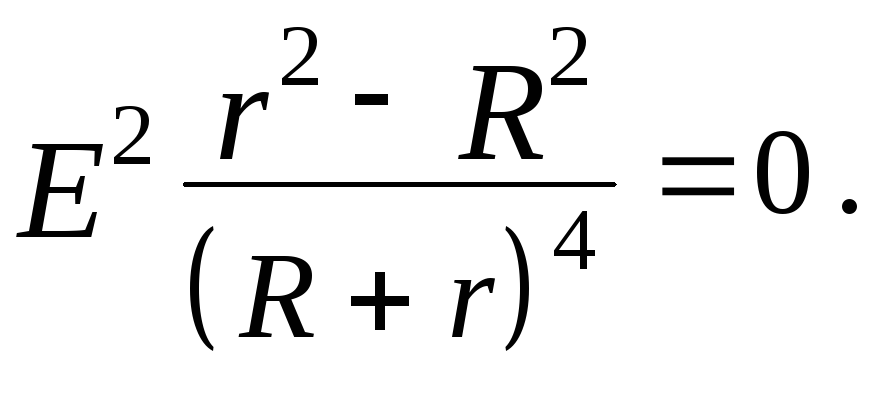Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
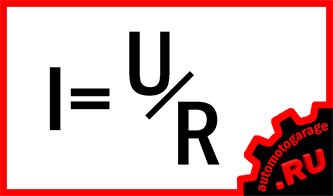
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
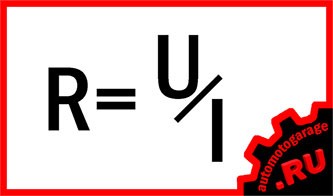
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
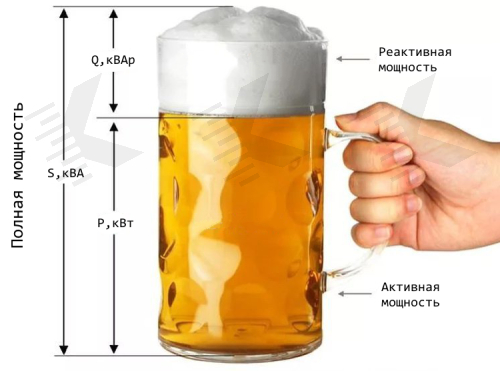
Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.
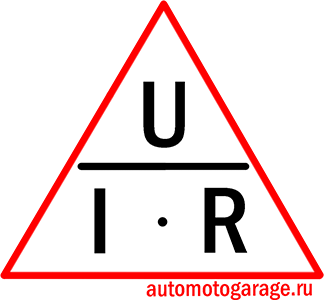
Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.
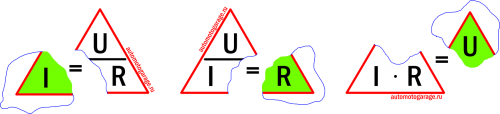
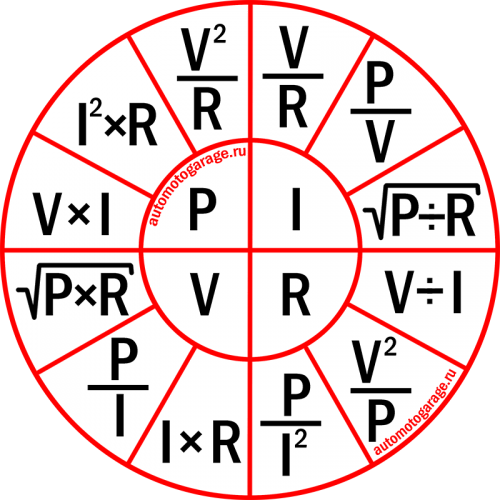
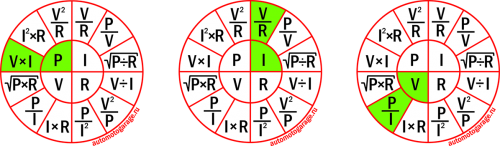
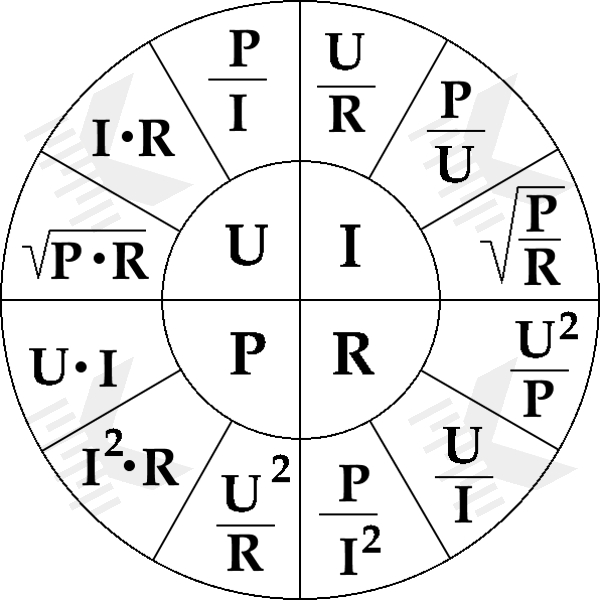
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.
Этот круг также, как и треугольник можно назвать магическим.
-
Александр (Гость)15 ноября 2020 / 07:52
-
Привет. У меня есть нерабочий строительный фен. Я нашёл, скажем так, новый нагреватель на замену нерабочего, но у него 3 вывода, т.е. на 2 рабочих положения. Но ещё одного вывода для запитки двигателя нет. Сопротивление обоих спиралей большое. Нагреватель я уже установил в корпус и вытаскивать его назад чревато поломкой. Вот я и подумал: возможно запитать двигатель автономным, не зависящим от спиралей, питанием. Двигатель, я думаю, на 12-18 вольт.
-
Павл (Гость)21 марта 2023 / 00:24
-
Удивляюсь. Люди не выставляют размерность, а потом предъяляют претензии автору.
Расчет кто-то в комментариях делал на 3кВ и 1МОм. Дело в том что калькулятор считает сначала верхнюю строку (I). Если силу тока выставить до расчёта в мкА или в мА, то и расчёт будет верный — 3000 мкА или 3 мА.
С 5В и 1000 Ом ещё проще. 5 вольт — это напряжение, например, выходное блока питания ЗУ (у телефона и т.д.). Его никто не меряет чисто в амперах, даже производитель ЗУ ставит маркировку в мА. Итого, вычисляем: 5В на 1кОм — это 5мА и 0.03Вт
Размерность, господа, размерность важна!
-
Матвей (Гость)6 апреля 2023 / 15:28
-
Калькулятор странный, например мне надо узнать какой будет ток, через резистор 2 вт 15 ом и 28 в
Выставляю эти значения, остается пустым сила тока, нажимаю рассчитать, а он сам меняет мощность на 52 вт, и уже от этого рисует мне 1.87А -
Вася (Гость)29 апреля 2023 / 10:37
-
Матвей. 1,87ампер потечет через резистор, а значит мощность нужна будет 52вт , для того, чтобы резистор выдержал на себе такое напряжение.
Рассмотрим
зависимость
полной, полезной и внутренней мощности
от внешнего
сопротивления
R
в цепи источника с ЭДС Е
и внутренним сопротивлением r.
Полнаямощность, развиваемая источником, может
быть записана следующим образом, если
в формулу (5) подставить выражение для
тока (1):
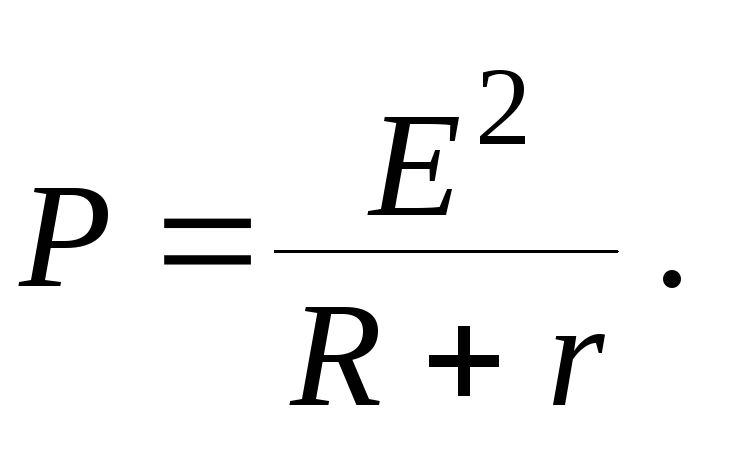
Так
полная мощность зависит от сопротивления
нагрузки R.
Она наибольшая при коротком замыкании
цепи, когда сопротивление нагрузки
обращается в нуль (9). С ростом сопротивления
нагрузки R
полная мощность уменьшается, стремясь
к нулю при R
.
На внешнем
сопротивлении выделяется
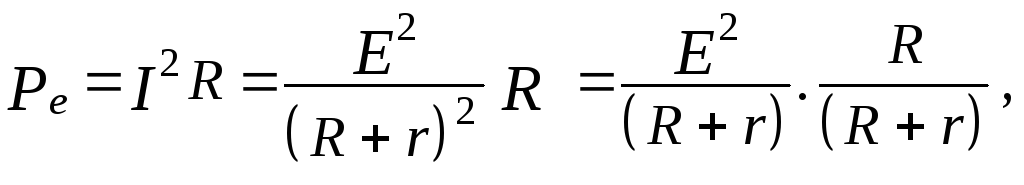
(20)
Внешняя
мощность Ре
составляет
часть полной мощности Р
и ее величина зависит от отношения
сопротивлений R/(R+r).
При коротком замыкании внешняя мощность
равна нулю. При увеличении сопротивления
R
она сначала увеличивается. При R
r
внешняя мощность по величине стремится
к полной. Но сама полезная мощность при
этом становится малой, так как уменьшается
полная мощность (см. формулу 18). При R
внешняя мощность стремятся к нулю как
и полная.
Каково
должно быть сопротивление нагрузки,
чтобы получить от данного источника
максимальную
внешнюю (полезную) мощность (19)?
Найдем
максимум этой функции из условия:
Решая
это уравнение, получаем Rmax=
r.
Таким
образом, во
внешней цепи выделяется максимальная
мощность, если ее сопротивление равно
внутреннему сопротивлению источника
тока. При
этом условии ток в цепи равен
E/2r,
т.е. половине
тока короткого замыкания (8). Максимальная
полезная мощность при таком сопротивлении
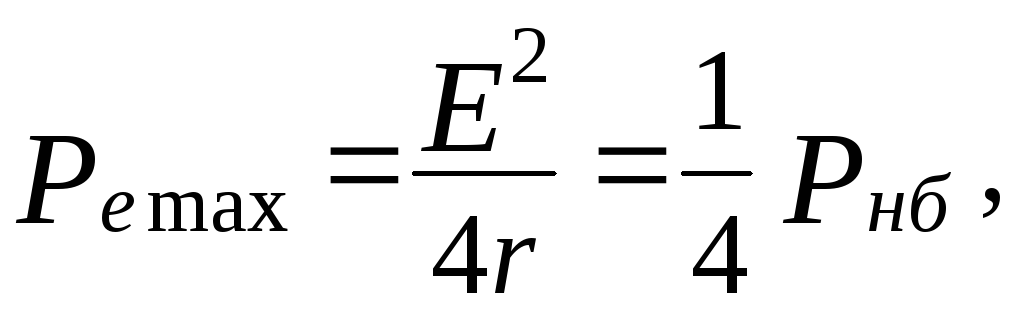
что
совпадает с тем, что было получено выше
(12).
Мощность, выделяющаяся
на внутреннем сопротивлении источника
(22)
При
R
PiP,
а при R=0
достигает наибольшей величины Pi
нб=Pнб=E2/r.
При R=r
внутренняя мощность составляет половину
полной, Pi=P/2.
При Rr
она уменьшается почти так же, как и
полная (18).
Зависимость
КПД от сопротивления внешней части цепи
выражается следующим образом:
=
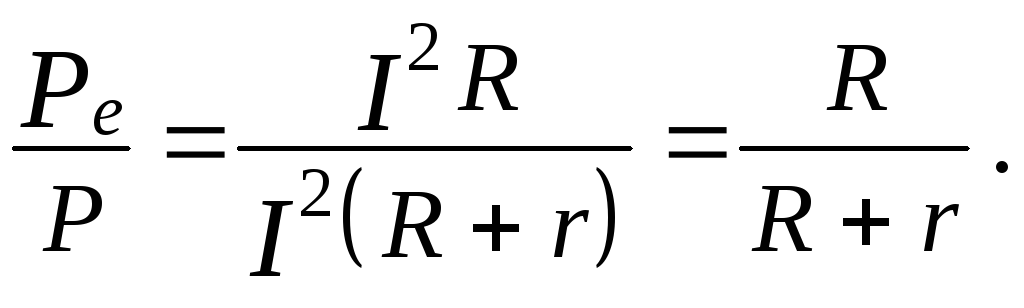
Из
полученной формулы вытекает, что КПД
стремится к нулю при приближении
сопротивления нагрузки к нулю, и КПД
стремится к наибольшему значению,
равному единице, при возрастании
сопротивления нагрузки до
R
r
. Но полезная мощность при этом уменьшается
почти как 1/R
(см. формулу
19).
Мощность
Ре
достигает максимального значения при
Rmax=
r,
КПД при этом равен, согласно формуле
(23),
= r/(r+r)
= 1/2. Таким
образом, условие
получения максимальной полезной мощности
не совпадает с условием получения
наибольшего КПД.
Наиболее
важным результатом проведенного
рассмотрения является оптимальное
согласование параметров источника с
характером нагрузки. Здесь можно выделить
три области: 1)R
r,
2)R
r,
3) R
r.
Первый
случай имеет место там, где от источника
требуется малая мощность в течение
длительного времени, например, в
электронных часах, микрокалькуляторах.
Размеры таких источников малы, запас
электрической энергии в них небольшой,
она должна расходоваться экономно,
поэтому они должны работать с высоким
КПД.
Второй
случай – короткое замыкание в нагрузке,
при котором вся мощность источника
выделяется в нем и проводах, соединяющих
источник с нагрузкой. Это приводит к их
чрезмерному нагреванию и является
довольно распространенной причиной
возгораний и пожаров. Поэтому короткое
замыкание источников тока большой
мощности (динамо-машины, аккумуляторные
батареи, выпрямители) крайне опасно.
В третьемслучае от источника хотят получить
максимальную мощность хотя бы накороткоевремя, например, при запуске двигателя
автомобиля с помощью электростартера,
величина КПД при этом не так уж важна.
Стартер включается на короткое время.
Длительная эксплуатация источника в
таком режиме практически недопустима,
так как она приводит к быстрому разряду
автомобильного аккумулятора, его
перегреву и прочим неприятностям.
Для обеспечения
работы химических источников тока в
нужном режиме их соединяют между собой
определенным образом в так называемые
батареи. Элементы в батарее могут
соединяться последовательно, параллельно
и по смешанной схеме. Та или иная схема
соединения определяется сопротивлением
нагрузки и величиной потребляемого
тока.
Важнейшим
эксплуатационным требованием к
энергетическим установкам является
высокий КПД их работы. Из формулы (23 )
видно, что КПД стремится к единице, если
внутреннее сопротивление источника
тока мало по сравнению с сопротивлением
нагрузки
Параллельно
можно соединять элементы, имеющие
одинаковые
ЭДС. Если соединено n
одинаковых
элементов, то от такой батареи можно
получить ток
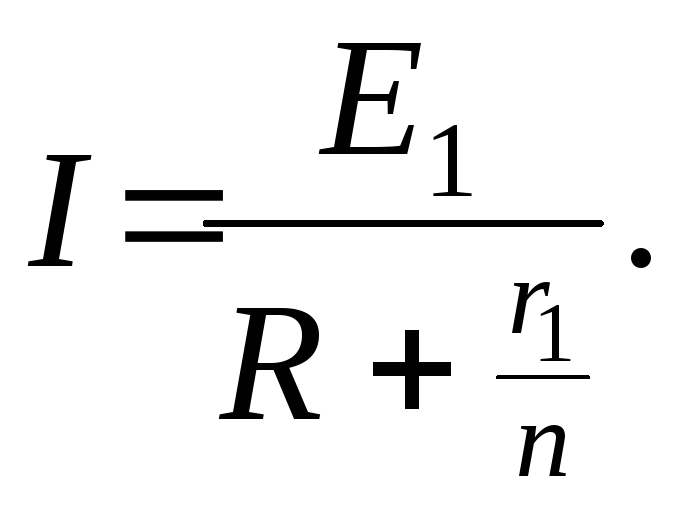
Здесь
r1
– сопротивление
одного элемента, Е1
– ЭДС одного
элемента.
Такое
соединение выгодно применять при
низкоомной нагрузке, т.е. при R
r.
Так как общее внутреннее сопротивление
батареи при параллельном соединении
уменьшается в n
раз по
сравнению с сопротивлением одного
элемента, то его можно сделать близким
сопротивлению нагрузки. Благодаря
этому увеличивается КПД источника.
Возрастает в n
раз и
энергетическая емкость батареи элементов.
Если
нагрузка высокоомная, т.е. R
r,
то выгоднее соединять элементы в батарею
последовательно. При этом ЭДС батареи
будет в n
раз больше
ЭДС одного элемента и от источника можно
получить необходимый ток
.
(25)
Целью
данной
лабораторной работы является
экспериментальная
проверка
полученных выше теоретических результатов
о зависимости полной, внутренней и
внешней (полезной) мощности и КПД
источника как от силы потребляемого
тока, так и от сопротивления нагрузки.
Описание
установки.
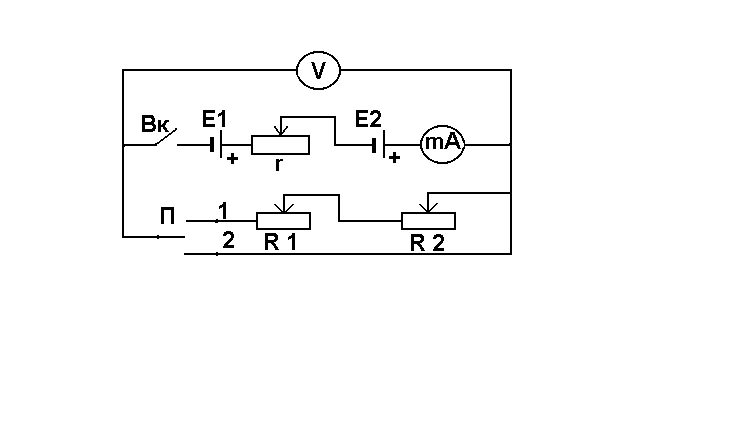
Для исследования рабочих характеристик
источника тока применяется электрическая
цепь, схема которой показана на рис. 4.
В качестве источника тока используются
два щелочных аккумулятора НКН-45, которые
соединяются
последователь-но
в одну батарею
через резистор r
, моделирующий
внутреннее сопро-тивление источника.
Его включение искусственно
увеличивает внутреннее сопротивление
аккуму-ляторов, что 1)защищает их от
перегрузки при переходе в режим короткого
замыкания и 2)дает возможность изменять
внутреннее сопротивление источника по
желанию экспериментатора. В качестве
нагрузки (внешнего сопротивления цепи)
п
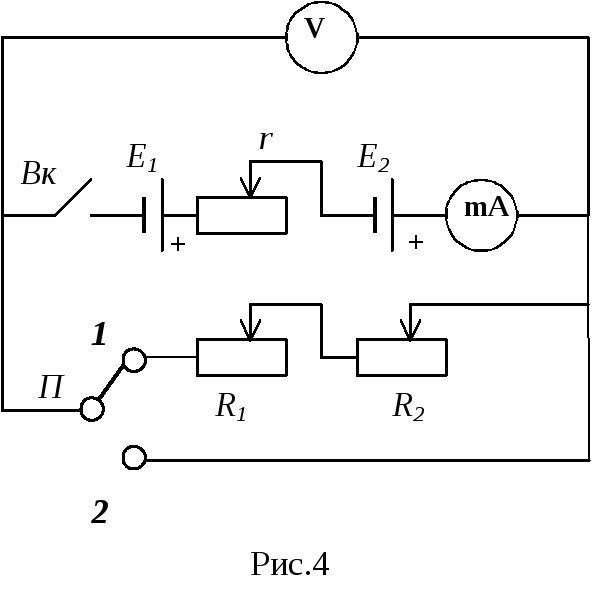
два переменных резистораR1
и R2.
(один грубой регулировки, другой –
тонкой), что обеспечивает плавное
регулирование тока в широком диапазоне.
Все приборы
смонтированы на лабораторной панели.
Резисторы закреплены под панелью, наверх
выведены их ручки управления и клеммы,
около которых имеются соответствующие
надписи.
Измерения.
1.Установите переключатель П
в нейтральное
положение, выключатель Вк
разомкните.
Ручки резисторов поверните против
часовой стрелки до упора ( это соответствует
наибольшему сопротивлению нагрузки).
-
Соберите
электрическую цепь по схеме (рис. 4), не
присоединяя
пока источники
тока. -
После
проверки собранной цепи преподавателем
или лаборантом присоедините аккумуляторы
Е1
и Е2
, соблюдая
полярность. -
Установите
ток короткого замыкания. Для этого
поставьте переключатель П
в положение 2 (внешнее сопротивление
равно нулю) и с помощью резистора r
установите
стрелку миллиамперметра на предельное
(правое крайнее) деление шкалы прибора
– 75 или 150 мА. Благодаря резистору r
в лабораторной установке есть возможность
регулировать
внутреннее сопротивление источника
тока. На самом деле внутреннее
сопротивление – величина постоянная
для данного типа источников и изменить
его невозможно. -
Поставьте
переключатель П
в положение 1,
включив тем самым внешнее сопротивление
(нагрузку) R=R1+R2
в цепь источника. -
Изменяя
ток в цепи через 5…10 мА от наибольшего
до наименьшего значения с помощью
резисторов R1
и
R2,
запишите показания миллиамперметра и
вольтметра (напряжение на нагрузке U)
в таблицу. -
Поставьте
переключатель П
в нейтральное положение. В этом случае
к источнику тока присоединен только
вольтметр, который обладает довольно
большим сопротивлением по сравнению
с внутренним сопротивлением источника,
поэтому показание вольтметра будет
чуть-чуть меньше ЭДС источник. Поскольку
у вас нет другой возможности определить
ее точное значение, остается принять
показание вольтметра за Е.
(Подробнее об этом см. в лабораторной
работе № 311).
|
№
пп |
I,
мА |
U, B |
E, B |
P, Вт |
Pe, Вт |
Pi, Вт |
R, Ом |
|
Обработка
результатов.
1. Для каждого значения тока вычислите:
-
полную мощность
по формуле (5), -
внешнюю
(полезную) мощность по формуле
,
-
внутреннюю
мощность из соотношения
-
сопротивление
внешнего участка цепи из закона Ома
R=U/I, -
КПД источника
тока по формуле (16).
-
Постройте графики
зависимостей:
-
полной,
полезной и внутренней мощности от тока
I
(на одном
планшете), -
полной,
полезной и внутренней мощности от
сопротивления R
(также на одном планшете); разумней
построить только часть графика,
соответствующего его низкоомной части,
и отбросить 4-5 экспериментальных точек
из 15 в высокоомной области, -
КПД
источника от величины потребляемого
тока I, -
КПД
от сопротивления нагрузки R.
-
Из
графиков Pe
от
I
и
Pe
от
R
определите
максимальную полезную мощность во
внешней цепи Pe
max. -
Из
графика Pe
от
R
определите
внутреннее сопротивление источника
тока r. -
Из
графиков Pe
от
I
и
Pe
от
R
найдите
КПД источника тока при Imax
и при
Rmax.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мощность резистора
Как рассчитать мощность резистора?
Мощность рассеивания резистора
У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.
Сама по себе мощность постоянного тока рассчитывается по простой формуле:
Здесь, P(Вт) – мощность;
U(В) – напряжение;
I(А) – ток.
Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.
Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше!
Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:
- 0,125 Вт
- 0,25 Вт
- 0,5 Вт
- 1 Вт
- 2 Вт
- Более 2 Вт.
Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.
Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?
Тут нам потребуется формула. Выглядит она так:
Здесь, P(Вт) – мощность;
R(Ом) – сопротивление цепи (в данном случае резистора);
I(А) – ток, протекающий через резистор.
Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).
Рассчитаем мощность для нашего резистора:
Мы получили мощность 1 Ватт. Теперь небольшое отступление.
В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.
Поэтому нам подойдёт резистор мощностью 2 Вт (см. стандартный ряд мощностей резисторов).
Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.
Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?
Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.
Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?
Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом — 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:
R1 – 20 Ом (0,5 Вт);
R2 – 80 Ом (1 Вт)
Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.
Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.
Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.
Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:
Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.
Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
-
Научись паять! Минимальный наборчик для пайки.
-
Научись паять! Подготовка и уход за паяльником.
Цепь постоянного тока (или, строго говоря, цепь без комплексного сопротивления)
Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока.
- P = мощность (Ватт)
- U = напряжение (Вольт)
- I = ток (Ампер)
- R = сопротивление (Ом)
- r = внутреннее сопротивление источнка ЭДС
- ε = ЭДС источника
- Тогда для всей цепи:
- I=ε/(R +r) — закон Ома для всей цепи.
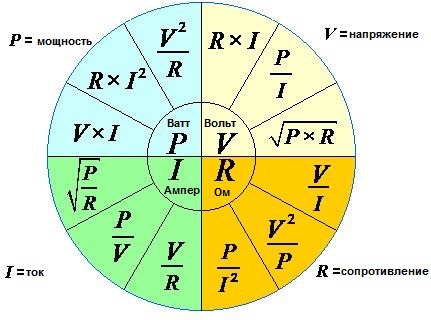
И еще ниже куча формулировок закона Ома для участка цепи :
|
Электрическое напряжение:
|
Электрическая мощность:
|
|
Электрический ток:
|
Электрическое сопротивление:
|
НЕ ЗАБЫВАЕМ: Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.
Цепь переменного синусоидального тока c частотой ω.
Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока и частоты.
Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, т.е. в предположении, что параметры сети
частотнонезависимы — данная формулировка применима ко всем гармоникам любого сигнала.
Закон Ома для цепей переменного тока:
-
U=I*Z
- где:
- Естественно, применительно к цепям переменного тока можно говорить и об активной/реактивной мощности.
- где:
- U = U0eiωt напряжение или разность потенциалов,
- I сила тока,
- Z = Re—iφ комплексное сопротивление (импеданс)
- R = (Ra2+Rr2)1/2 полное сопротивление,
- Rr = ωL — 1/ωC реактивное сопротивление (разность индуктивного и емкостного),
- Rа активное (омическое) сопротивление, не зависящее от частоты,
- φ = arctg Rr/Ra — сдвиг фаз между напряжением и током.
С помощью калькулятора мощности вы можете самостоятельно выполнить расчет мощности по току и напряжению для однофазных (220 В) и трехфазных сетей (380 В). Программа также рассчитывает мощность через сопротивление и напряжение, или через ток и сопротивление согласно закону Ома. Значение cos φ принимается согласно указаниям технического паспорта прибора, усредненным значениям таблиц ниже или рассчитываются самостоятельно по формулам. Без необходимости рекомендуем не изменять коэффициент и оставлять равным 0.95. Чтобы получить результат расчета, нажмите кнопку «Рассчитать».
Смежные нормативные документы:
- СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
- СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
- СП 76.13330.2016 «Электротехнические устройства»
- ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
- ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
- ГОСТ Р 50571.1-93 «Электроустановки зданий»
Формулы расчета мощности
Мощность — это физическая величина, равная отношению количества работы ко времени совершения этой работы.
Мощность электрического тока (P) — это величина, характеризующая скорость преобразования электрической энергии в другие виды энергии. Международная единица измерения — Ватт (Вт/W).
— Мощность по току и напряжению (постоянный ток): P = I × U
— Мощность по току и напряжению (переменный ток однофазный): P = I × U × cos φ
— Мощность по току и напряжению (переменный ток трехфазный): P = I × U × cos φ × √3
— Мощность по току и сопротивлению: P = I2 × R
— Мощность по напряжению и сопротивлению: P = U2 / R
- I – сила тока, А;
- U – напряжение, В;
- R – сопротивление, Ом;
- cos φ – коэффициент мощности.
Расчет косинуса фи (cos φ)
φ – угол сдвига между фазой тока и напряжения, причем если последний опережает ток сдвиг считается положительным, если отстает, то отрицательным.
cos φ – безразмерная величина, которая равна отношению активной мощности к полной и показывает насколько эффективно используется энергия.
Формула расчета косинуса фи: cos φ = S / P
- S – полная мощность, ВА (Вольт-ампер);
- P – активная мощность, Вт.
Активная мощность (P) — реальная, полезная, настоящая мощность, эта нагрузка поглощает всю энергию и превращает ее в полезную работу, например, свет от лампочки. Сдвиг по фазе отсутствует.
Формула расчета активной мощности: P (Вт) = I × U × cos φ
Реактивная мощность (Q) — безваттная (бесполезная) мощность, которая характеризуется тем, что не участвует в работе, а передается обратно к источнику. Наличие реактивной составляющей считается вредной характеристикой цепи, поскольку главная цель существующего электроснабжения — это сокращение издержек, а не перекачивание ее туда и обратно. Такой эффект создают катушки и конденсаторы.
Формула расчета реактивной мощности: P (ВАР) = I × U × sin φ
Полная мощность электроприбора (S) — это суммарная величина, которая включает в себе как активную, так и реактивную составляющие мощности.
Формула расчета полной мощности: S (ВА) = I × U или S = √( P2 + Q2)
Косинус фи для различных потребителей – таблица
| Наименование электроприбора | cos φ |
| Бойлер | 1 |
| Болгарка | 0.8 |
| Вакуумный насос | 0.85 |
| Индукционные печи | 0.85 |
| Компрессор | 0.7 |
| Компьютер | 0.95 |
| Кофеварка | 1 |
| Лампы газоразрядные | 0.4-0.6 |
| Лампы люминисцентные | 0.95 |
| Лампы накаливания | 1 |
| Обогреватель | 1 |
| Перфоратор | 0.85 |
| Пылесос | 0.9 |
| СВЧ-печь | 1 |
| Стиральная машина | 0.9 |
| Телевизор | 1 |
| Утюг | 1 |
| Фен | 1 |
| Холодильник | 0.95 |
| Электродрель | 0.85 |
| Электромоторы | 0.7-0.8 |
| Электроплита | 1 |
| Электросварка дуговая | 0.3-0.6 |
| Электрочайник | 1 |