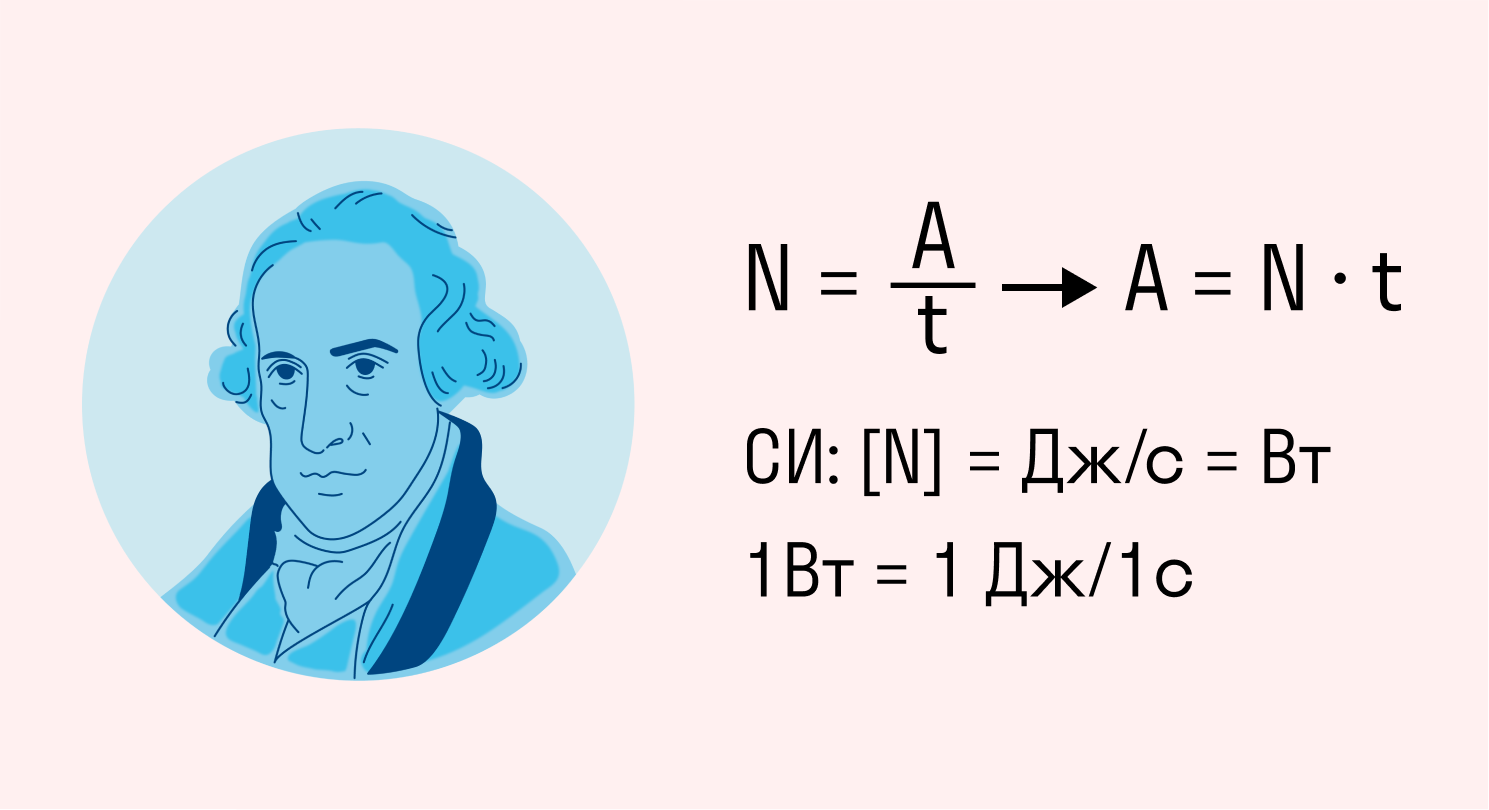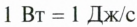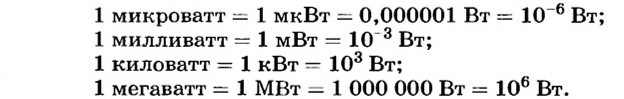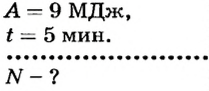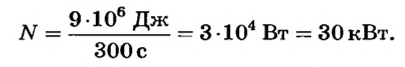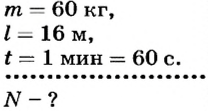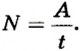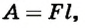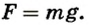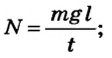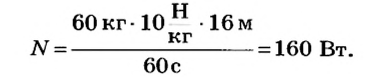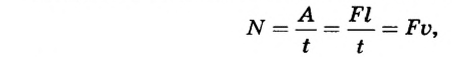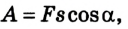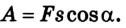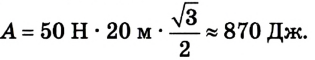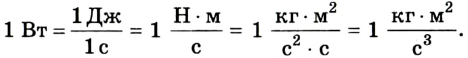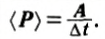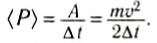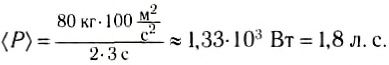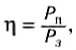Определение мощности
Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.
Мощность в физике — это количество работы, которая совершается за единицу времени.
Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
В электромеханике эта величина имеет еще одно определение.
Мощность — это скалярная физическая величина, которая характеризует мгновенную скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии.
Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).
Мощность человека в зависимости от деятельности
|
Вид деятельности |
Мощность, Вт |
|---|---|
|
Неспешная ходьба |
60–65 |
|
Бег со скоростью 9 км/ч |
750 |
|
Плавание со скоростью 50 м/мин |
850 |
|
Игра в футбол |
930 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Как обозначается мощность: единицы измерения
В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.
Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.
В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.
Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.
В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.
Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.
Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴
|
Единицы измерения |
Вт |
|---|---|
|
1 ватт |
1 |
|
1 киловатт |
103 |
|
1 мегаватт |
106 |
|
1 эрг в секунду |
10-7 |
|
1 метрическая лошадиная сила |
735,5 |
Подготовка к ОГЭ по физике онлайн поможет снять стресс перед экзаменом и получить высокий балл.
Все формулы мощности
Зная определения, несложно понять формулы мощности, используемые в разных разделах физики — в механике и электротехнике.
В механике
Механическая мощность (N) равна отношению работы ко времени, за которое она была выполнена.
Основная формула:
N = A / t, где A — работа, t — время ее выполнения.
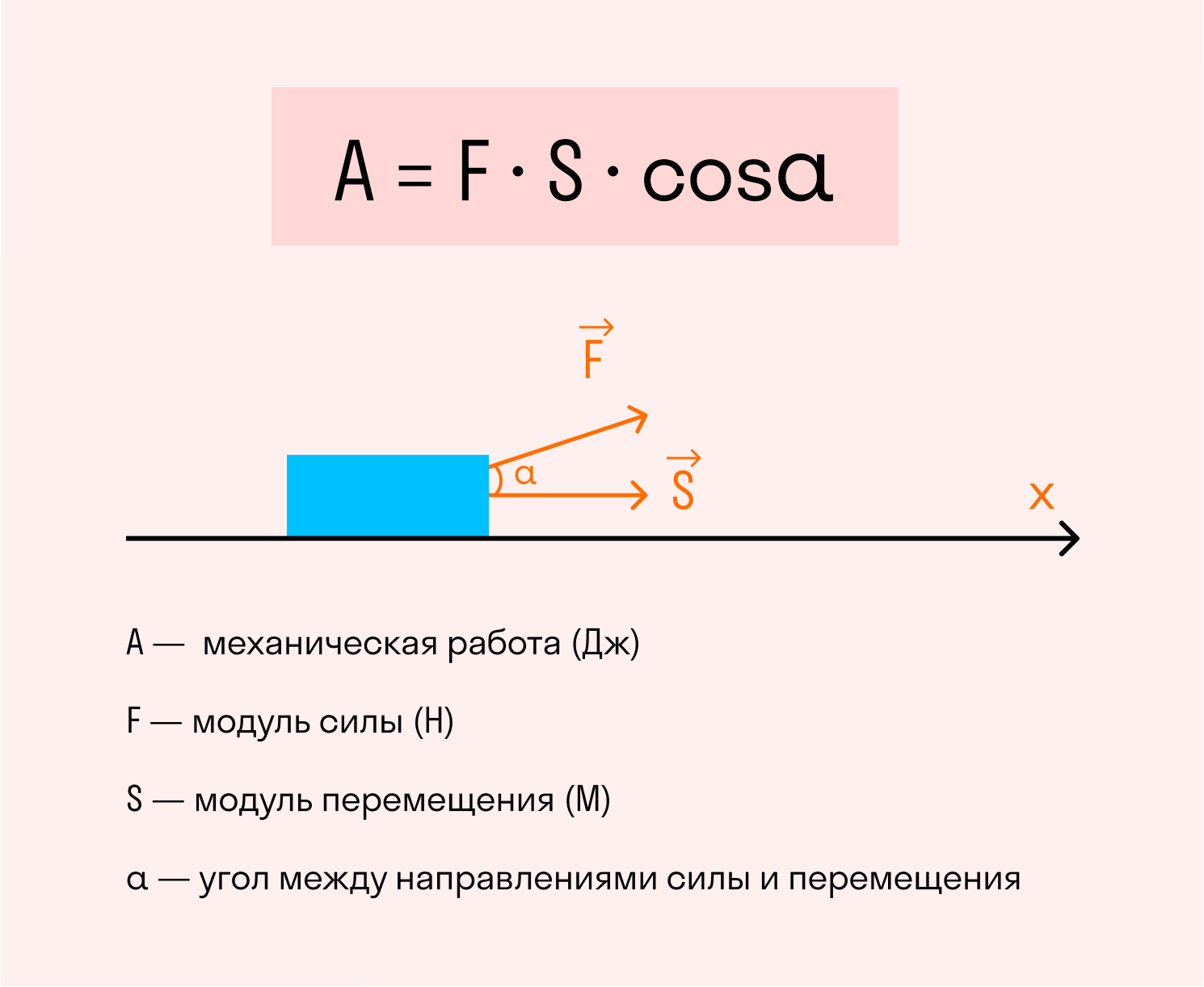
Если вспомнить, что работой называется произведение модуля силы, модуля перемещения и косинуса угла между ними, мы получим формулу измерения работы.
Если направления модуля приложения силы и модуля перемещения объекта совпадают, угол будет равен 0 градусов, а его косинус равен 1. В таком случае формулу можно упростить:
A = F × S
Используем эту формулу для вычисления мощности:
N = A / t = F × S / t = F × V
В последнем выражении мы исходим из того, что скорость (V) равна отношению перемещения объекта на время, за которое это перемещение произошло.
В электротехнике
В общем случае электрическая мощность (P) говорит о скорости передачи энергии. Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.
P = I × U, где I — сила тока, U — напряжение.
В электротехнике существует несколько видов мощности: активная, реактивная, полная, пиковая и т. д. Но это тема отдельного материала, сейчас же мы потренируемся решать задачи на основе общего понимания этой величины. Посмотрим, как найти мощность, используя вышеуказанные формулы по физике.
Задача 1
Допустим, человек поднимает ведро воды из колодца, прикладывая силу 60 Н. Глубина колодца составляет 10 м, а время, необходимое для поднятия — 30 сек. Какова будет мощность человека в этом случае?
Решение:
Найдем вначале величину работы, используя тот факт, что мы знаем расстояние перемещения (глубину колодца 10 м) и приложенную силу 60 Н.
A = F × S = 60 Н × 10 м = 600 Дж
Когда известно значение работы и времени, найти мощность несложно:
N = A / t = 600 Дж / 30 сек = 20 Вт
Ответ: мощность человека при поднятии ведра — 20 ватт.
Задача 2
В комнате включена лампа мощностью 100 Вт. Напряжение домашней электросети — 220 В. Какая сила тока проходит через эту лампу?
Решение:
Мы знаем, что Р = 100 Вт, а U = 220 В.
Поскольку P = I × U, следовательно I = P / U.
I = 100 / 220 = 0,45 А.
Ответ: через лампу пройдет сила тока 0,45 А.
Вопросы для самопроверки
-
Что характеризует механическая мощность?
-
Какие существуют единицы измерения мощности в физике?
-
Какая из единиц измерения считается устаревшей?
-
Мощность можно назвать скалярной величиной? Что это означает?
-
Как из формулы нахождения мощности получить работу?
-
Какой буквой обозначается мощность в механике, а какой — в электротехнике?
-
Какую работу производит за 30 минут устройство мощностью 600 Вт?
-
Как узнать напряжение в сети, если мы знаем мощность подключенного к ней прибора и силу тока, проходящую через прибор?
-
Если в течение 1 часа автомобиль №1 едет со скоростью 60 км/ч, а автомобиль №2 — со скоростью 90 км/ч, одинаковую ли мощность они развивают в это время?
-
Допустим, автобус отвез пассажиров из города А в город В за 1 час. Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
Содержание:
Мощность:
Одинаковую работу можно совершить за разные промежутки времени. Например, можно поднять груз за минуту, а можно поднимать этот же груз в течение часа.
Физическую величину, равную отношению совершенной работы
Единицей мощности в SI является джоуль в секунду (Дж/с), или ватт (Вт), названный так в честь английского изобретателя Дж. Уатта. Один ватт — это такая мощность, при которой работу в 1 Дж совершают за 1 с. Итак,
Человек может развивать мощность в сотни ватт. Чтобы оценить, насколько могущество человеческого разума, создавшего двигатели, больше «могущества» человеческих мускулов, приведем такие сравнения:
- мощность легкового автомобиля примерно в тысячу раз больше средней мощности человека;
- мощность авиалайнера примерно в тысячу раз больше мощности автомобиля;
- мощность космического корабля примерно в тысячу раз больше мощности самолета.
Мощность
Механическая работа всегда связана с движением тел. А движение происходит во времени. Поэтому и выполнение работы, как и превращение механической энергии, всегда происходит на протяжении определенного времени.
Работа выполняемая на протяжении определенного времени:
Простейшие наблюдения показывают, что время выполнения работы может быть разным. Так, школьник может подняться по лестнице на пятый этаж за 1-2 мин, а пожилой человек — не меньше чем за 5 мин. Грузовой автомобиль КрАЗ может перевезти определенный груз на расстояние 50 км за 1 ч. Но если этот груз частями начнет перевозить легковой автомобиль с прицепом, то потратит на это не меньше 12 ч.
Для описания процесса выполнения работы, учитывая его скорость, используют физическую величину, которая называется мощностью.
Что такое мощность
Мощность — это физическая величина, которая показывает скорость выполнения работы и равна отношению работы ко времени, за которое эта работа выполняется.
Так как при выполнении работы происходит превращение энергии, то можно считать, что мощность характеризует скорость превращения энергии.
Как рассчитать мощность
Для расчета мощности нужно значение работы разделить на время, за которое эта работа была выполнена:
Если мощность обозначить латинской буквой 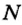
Единицы мощности
Для измерения мощности используется единица ватт (Вт). При мощности 1 Вт работа 1 Дж выполняется за 1 с:
Единица мощности названа в честь английского механика Джеймса Уатта, который внес значительный вклад в теорию и практику построения тепловых двигателей.

Главная заслуга Уатта в том, что он отделил водяной конденсатор от нагревателя и сконструировал насос для охлаждения конденсатора. Фактически он увеличил разность температур между нагревателем и конденсатором (холодильником), благодаря чему увеличил экономичность паровой машины. Позже теоретически это обоснует Сади Карно.
Он один из первых высказал предположение, что вода — это сложное вещество, состоящее из водорода и кислорода.
Как и для других физических величин, для единицы мощности существуют производные единицы:
Пример №1
Определить мощность подъемного крана, если работу 9 МДж он выполняет за 5 мин.
Дано:
Решение
По определению 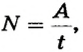
Ответ. Мощность крана 30 кВт.
Пример №2
Человек массой 60 кг поднимается на пятый этаж дома за 1 мин. Высота пяти этажей дома равна 16 м. Какую мощность развивает человек?
Дано:
Решение
По определению
Работа определяется
Тогда
Ответ. Человек развивает мощность 160 Вт.
Зная мощность и время, можно рассчитать работу:
Скорость движения зависит от мощности
Мощность связана со скоростью соотношением:
где 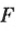
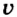
Если известны мощность двигателя и значения сил сопротивления, то можно рассчитать возможную скорость автомобиля или другой машины, которая выполняет работу:
Таким образом, из двух автомобилей при равных силах сопротивления большую скорость будет иметь тот, у которого мощность двигателя больше.
Каждый конструктор знает, что для увеличения скорости движения автомобиля, самолета или морского корабля нужно или увеличивать мощность двигателя, или уменьшать силы сопротивления. Поскольку увеличение мощности связано с увеличением потребления топлива, то средствам современного транспорта, как правило, придают специфическую обтекаемую форму, при которой сопротивление воздуха будет наименьшим, а все подвижные части изготавливают так, чтобы сила трения была минимальной.
Итоги:
- Существуют два вида механической энергии: кинетическая и потенциальная.
- Если тело перемещается или деформируется под действием силы, то выполняется механическая работа.
- Простыми механизмами являются рычаги и блоки.
- Ни один простой механизм не дает выигрыша в работе.
- Качество механизма определяется коэффициентом полезного действия, который определяет часть полезной работы в общей выполненной работе.
- Тело, при перемещении которого может быть выполнена работа, обладает энергией.
- Взаимодействующие тела обладают потенциальной энергией.
- Движущееся тело обладает кинетической энергией, которая зависит от скорости и массы тела.
- Потенциальная и кинетическая энергии могут превращаться друг в друга. Такие превращения происходят в равной мере, если отсутствуют силы трения.
- Сумму кинетической и потенциальной энергий называют полной механической энергией системы.
- В замкнутой системе при отсутствии сил трения сумма кинетической и потенциальной энергий остается постоянной.
- Закон сохранения и превращения энергии подтверждает невозможность существования вечного двигателя (perpetuum mobile).
- Мощность характеризует скорость превращения одного вида энергии в другой.
Механическая работа и мощность
С помощью импульса невозможно описать все случаи взаимодействия. Поэтому в физике применяют еще и понятие механической работы.
В механике работа зависит от значения и направления силы, а также перемещения точки ее приложения. Из курса физики 8 класса вам известно, что
A = Fs,
где F — значение силы, действующей на тело; s — модуль перемещения тела.
Если сила F постоянна, а перемещение 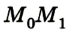
где s = 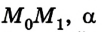
Робота является величиной скалярной. Произведение 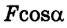
Легко заметить, что если 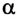
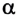
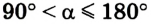
Пример №3
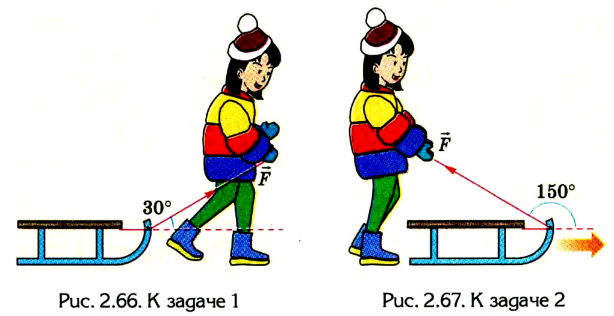
Девочка тянет санки равномерно, прикладывая к веревке силу 50 Н. Веревка натягивается под углом 30° к горизонту (рис. 2.66). Какую работу выполнит девочка, переместив санки на 20 м?
Дано:
F = 50 Н,
s = 20 м, 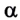
А-?
Решение
По определению
Соответственно
Ответ: А = 870 Дж (работа силы положительная, поскольку cos 30° > 0).
- Заказать решение задач по физике
Пример №4
Решим предыдущую задачу для случая, когда девочка удерживает санки, съехавшие с горки (рис. 2.67). В данном случае 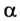
Дано:
F = 50 Н, s = 20 м,
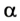
А — ?
Решение
А = Fscosa;
А = 50 Н • 20 м • (-0,87) 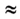
Ответ: А = -870 Дж (работа силы отрицательная, поскольку cos 150° < 0).
Таким образом, в зависимости от направления действия силы по отношению к перемещению работа может иметь положительные и отрицательные значения.
Например, работа, которую выполняет двигатель автомобиля, будет положительной, поскольку направление силы тяги автомобиля совпадает с направлением его движения. Положительной будет и работа человека, поднимающего какой-либо груз с земли на определенную высоту. Силы трения, действующие на автомобиль, выполняют отрицательную работу, поскольку направлены в противоположном направлении к перемещению.
Возможны случаи, когда работа равна нулю, хотя перемещение тела происходит. Например, если 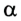
Мощность — это физическая величина, характеризующая скорость совершения работы. Поскольку во время выполнения работы происходит превращение энергии, можно сделать вывод, что мощность показывает скорость превращения одного вида энергии в другой.
В механике мощность обозначают буквой N и рассчитывают по формуле
N= — =—,
t t
где 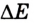
Если известны мощность и время, за которое совершена работа, то можно рассчитать и саму работу:
A = Nt.
Основная единица измерения мощности — ватт (Вт):
Всё о мощности
Одна и та же работа в разных случаях может быть выполнена за различные промежутки времени, т. е. она может совершаться неодинаково быстро. Например, при подъеме груза на определенную высоту подъемным краном (рис. 148) будет затрачено гораздо меньше времени, чем при использовании лебедки.
Для характеристики процесса выполнения работы важно знать не только ее численное значение, но и время, за которое она выполняется. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.
Величина, характеризующая быстроту совершения работы, называется мощностью. Ее обычно обозначают буквой Р.
Если в течение промежутка времени Δt была совершена работа А, то средняя мощность равна отношению работы к этому промежутку времени:
Из определения видно, что мощность численно равна работе, совершаемой в единицу времени. Таким образом, единицей мощности является джоуль в секунду 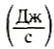
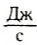
Понятно, что во времена Уатта на заре технической революции мощность построенной паровой машины было естественно сравнить с мощностью лошади — единственным в то время «двигателем».
Может ли человек развивать мощность, равную 1 л. с.? Ответ на этот вопрос положительный. Рассмотрим разбег спортсмена на короткие дистанции. Хорошие спортсмены дистанцию в 100 м пробегают за 10 с, т. е. их средняя скорость 10 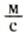
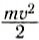
Если предположить, что масса спортсмена т = 80 кг, то
Разумеется, развивать такую мощность длительное время не сможет даже очень тренированный человек.Если известна мощность, то работа выражается равенством:
A = P∆t. (2)
Это позволяет ввести еще одну единицу работы (а значит, и энергии) следующим путем. За единицу работы можно принять работу, которая совершается некоторой силой в течение 1 с при мощности в 1 Вт. Она называется ватт-секундой. Понятно, что 1 Вт.c = 1 Дж. Часто используются более крупные внесистемные единицы работы и энергии: киловатт-час (кВт.ч) и мегаватт-час (МВт . ч):
1 кВт .ч= 1000кВт.3600 с = 3,6∙ 106 Дж;
1 МВт.ч= 1000кВт.3600 с = 3,6∙ 109 Дж.
При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.
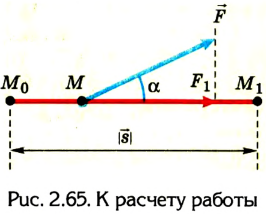
Наиболее общее выражение для работы постоянной силы, направленной под углом 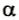
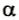
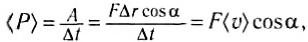
так как 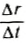
Ясно, что если модуль силы в некоторой момент времени равен F и модуль мгновенной скорости υ, а угол между ними 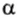
P = Fυcos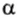
Как следует из формулы (4), при заданной мощности мотора сила тяги тем меньше, чем больше скорость движения автомобиля. Вот почему водители при подъеме в гору, когда нужна наибольшая сила тяги, переключают двигатель на пониженную передачу. Для движения по горизонтальному участку с постоянной скоростью достаточно, чтобы сила тяги преодолевала силу сопротивления движению. Формула (4) позволяет объяснить, что быстроходные поезда, автомобили, корабли, самолеты нуждаются в двигателях большой мощности и конструкции, обеспечивающей как можно меньшую силу сопротивления.
Любой двигатель или механическое устройство предназначены для выполнения определенной механической работы. Эта работа называется полезной работой. Для двигателя автомобиля — это работа по его перемещению, для токарного станка — работа по вытачиванию детали и т. п.
В любой машине, в любом двигателе полезная работа всегда меньше той энергии, которая затрачивается для приведения их в действие, потому что всегда существуют силы трения, работа которых приводит к нагреванию каких-либо частей устройства. А нагревание нельзя считать полезным результатом действия машины.
Поэтому каждое устройство характеризуется особой величиной, которая показывает, насколько эффективно используется подводимая к нему энергия. Эта величина называется коэффициентом полезного действия (КПД) и обычно обозначается греческой буквой η (эта).
Коэффициентом полезного действия называется отношение полезной )аботы, совершенной машиной за некоторый промежуток времени, ко всей утраченной работе (подведенной энергии) за тот же промежуток времени:
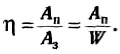
Коэффициент полезного действия обычно выражается в процентах, поскольку и полезную, и затраченную работы можно представить как произведение мощности на промежуток времени, в течение которого работала машина, то коэффициент полезного действия можно определить следующим образом:
где Pn и Р3 — полезная мощность и затраченная мощность соответственно.
Главные выводы:
- Мощность численно равна работе, которую совершает сила в единицу времени.
- Мощность силы равна произведению силы на скорость тела и косинус угла между направлением силы и скорости в данный момент времени.
- Коэффициентом полезного действия называется отношение полезной работы, совершенной машиной за некоторый промежуток времени, ко всей затраченной работе (подведенной энергии) за тот же промежуток времени.
- Взаимодействие тел
- Механическая энергия и работа
- Золотое правило механики
- Потенциальная энергия
- Криволинейное движение
- Ускорение точки при ее движении по окружности
- Инерциальные системы отсчета
- Энергия в физике
Не уверен в ответе?
Найди верный ответ на вопрос ✅ «Как найти мощность если известно масса высота и время? …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Содержание:
- Определение и формулы мощности
- Единицы измерения мощности
- Примеры решения задач
Определение и формулы мощности
Определение
Мощностью некоторой силы является скалярная физическая величина, которая характеризует скорость произведения работы данной силой. Мощность часто обозначают буквами: N, P.
$$P=frac{Delta A}{Delta t}(1)$$
В том случае, если за равные малые промежутки времени выполняется разная работа, то мощность является переменной во времени.
Тогда вводят мгновенное значение мощности:
$$P=lim _{Delta t rightarrow 0} frac{delta A}{Delta t}=frac{d A}{d t}$$
где $delta A$ – элементарная работа, которую выполняет сила,
$Delta t$ – отрезок времени в течение, которого данная работа была выполнена.
Если мгновенная мощность не является постоянной величиной, то выражение (1) определяет среднюю мощностьза время
$Delta t$.
Мощность силы можно определить как скалярное произведение силы на скорость, с которой движется точка приложения рассматриваемой силы:
$$P=bar{F} bar{v}=F_{tau} v$$
где $F_{tau}$ – проекция силы
$bar{F}$ на направление вектора скорости (
$bar{v}$).
При поступательном движении некоторого тела, имеющего массу m под воздействием силы
$bar{F}$ мощность можно вычислить, применяя формулу:
$$P=m v dot{v}(4)$$
В общем случае произвольного перемещения твердого тела суммарная мощность есть алгебраическая сумма мощностей всех сил,
которые действуют на тело:
$$P=sum_{i=1}^{k} bar{F}_{i} cdot bar{v}_{i}(5)$$
где $bar{v}_{i}$ – скорость перемещения точки, к которой приложена сила
$bar{F}_{i}$.
В случае поступательного движения твердого тела со скоростью $bar{v}$ мощность можно определить при помощи формулы:
$$P=overline{F v}(6)$$
где $bar{F}$ – главный вектор внешних сил.
Если твердое тело совершает вращение вокруг точки О или вокруг неподвижной оси, которая проходит через точку О, то формулой для счет мощности можно считать выражение:
$$P=bar{M} bar{omega}(7)$$
где $bar{M}$ – главный момент внешних сил по отношению к точке О,
$bar{omega}$ – мгновенная угловая скорость вращения тела.
Единицы измерения мощности
Основной единицей измерения мощности силы в системе СИ является: [P]=вт (ватт)
В СГС: [P]=эрг/с.
1 вт=107 эрг/( с).
Примеры решения задач
Пример
Задание. Какова мощность (P(t)), развиваемая силой, если она действует на тело, которое имеет массу m и
под воздействием приложенной силы движется поступательно. Сила описывается законом:
$F(t)=2 t cdot bar{i}+3 t^{2} bar{j}$
Решение. В качестве основы для решения задачи используем формулу для мощности вида:
$$P=F cdot v(1.1)$$
Из второго закона Ньютона мы имеем:
$$F=m a rightarrow a=frac{F}{m} ; v=int a d t=int frac{F}{m} d t=frac{1}{m} int F d t(1.2)$$
В выражение (2.2) подставим уравнение, заданное в условии задачи для F(t), имеем:
$$v=frac{1}{m} intleft(2 t cdot bar{i}+3 t^{2} bar{j}right) d t=frac{1}{m}left(t^{2} cdot bar{i}+t^{3} bar{j}right)(1.3)$$
Подставим выражение для скорости из (1.3) в (1.1), получим:
$$P=left(2 t cdot bar{i}+3 t^{2} bar{j}right) frac{1}{m}left(t^{2} cdot bar{i}+t^{3} bar{j}right)=frac{1}{m}left(2 t^{3}+3 t^{5}right)$$
Ответ. $P=frac{1}{m}left(2 t^{3}+3 t^{5}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
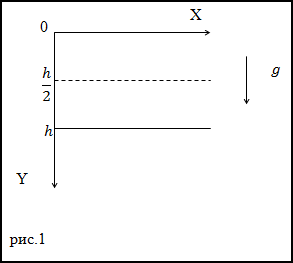
Задание. Какова мгновенная мощность силы тяжести на высоте h/2. если камень массы m падает с высоты h. Сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для мгновенной мощности вида:
$$P=bar{F} cdot bar{v}(2.1)$$
Сила, действующая на тело – сила тяжести. Она направлена по оси Y, выражение для ее проекции на ось Y запишем как:
$$F=m g(2.2)$$
В начальный момент времени тело имело скорость равную нулю, тогда скорость тела в проекции на ось Y можно вычислить, используя выражение:
$$v=v_{0}+g t=g t(2.3)$$
где v0=0.
Найдем момент времени, в который тело окажется на половине высоты (y=h/2), применим уравнение, которое описывает равноускоренное
движение (из начальных условий y0=0, v0=0):
$$y=y_{0}+v_{0} t+frac{g t^{2}}{2}=frac{g t^{2}}{2}=frac{h}{2} rightarrow t=sqrt{frac{h}{g}}(2.4)$$
Используем выражения (2.2), (2.3), (2.4) подставим в (2.1), получим искомую мгновенную мощность силы тяжести на половине пути свободно падающего тела:
$$P=m g cdot g sqrt{frac{h}{g}}=m sqrt{g^{3} h}$$
Ответ. $P=m sqrt{g^{3} h}$
Читать дальше: Формула плотности вещества.
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.
Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности