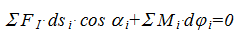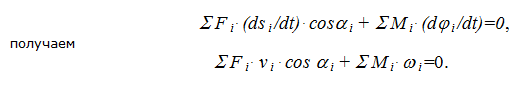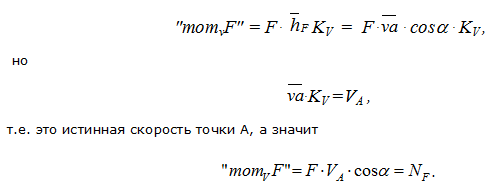Момент силы. Условия равновесия рычага
- Устройство и виды рычагов
- Момент силы
- Правило моментов для двух сил
- Правило моментов для нескольких сил
- Применение рычагов в быту и технике
- Задачи
- Лабораторная работа №9. Проверка условия равновесия рычага
п.1. Устройство и виды рычагов
 |
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
Рычаг состоит из перекладины и опоры. Назначение рычага – получить выигрыш в силе или расстоянии. |
В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.
п.2. Момент силы
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
На рисунке (l_1) – плечо силы (F_1, l_2) — плечо силы (F_2).
Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.
Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.
На рисунке сила (F_1) вращает рычаг против часовой стрелки, а сила (F_2) — по часовой стрелке.
Момент силы – это произведение силы, вращающей тело, на её плечо. $$ M=Fl $$ В системе СИ единица измерения момента силы — Н·м.
Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.
п.3. Правило моментов для двух сил
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
$$ F_1l_1=F_2l_2 $$ |
п.4. Правило моментов для нескольких сил
Правило моментов для нескольких сил
Рычаг находится в равновесии, если сумма моментов всех сил, вращающих его по ходу часовой стрелки, равен сумме моментов всех сил, вращающих его против хода часовой стрелки.
Например:
 |
Силы (F_1, F_2, F_3) вращают рычаг против часовой стрелки, а сила (F_4) — по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$ |
п.5. Применение рычагов в быту и технике
Рычаги первого рода
 Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры. |
 Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект. |
 Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя. |
 Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз. |
 Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом. |
 Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям. |
Рычаги второго рода
Рычаги третьего рода
п.6. Задачи
Задача 1. Для каждого положения тела укажите плечо силы.
При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.
Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.
Дано:
(frac{l_1}{l_2}=frac 15)
(m_1=2,5 text{кг})
__________________
(m_2-?)
По правилу моментов begin{gather*} F_1l_1=F_2l_2 end{gather*} На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g, F_2=m_2g $$ Получаем: begin{gather*} m_1gl_1=m_2gl_2\[7pt] m_2=frac{m_1l_1}{l_2} end{gather*} Подставляем: $$ m_2=2,5cdot frac 15=0,5 (text{кг}) $$ Ответ: 0,5 кг
Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
Дано:
(F_1=15 text{Н})
(F_2=60 text{Н})
(l_1+l_2=1 text{м})
__________________
(l_1, l_2-?)
По правилу моментов begin{gather*} F_1l_1=F_2l_2. end{gather*} Получаем систему уравнений begin{gather*} left{ begin{array}{l l} 15l_1=60l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 4l_2+l_2=1 end{array} right. Rightarrow \[7pt] Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 5l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=0,8 \ l_2=0,2 end{array} right. end{gather*} Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.
Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. Расстояние от точки подвеса груза к одному из концов балки в 4 раза больше, чем к другому. С какой силой балка давит на каждую из опор? Примите (gapprox 10 text{м/с}^2). Ответ запишите в килоньютонах.
Дано:
(m=500 text{кг})
(gapprox 10 text{м/с}^2)
(OB=4OA)
__________________
(F_A, F_B-?)
Сила тяжести (F_{text{т}}=mg), направленная вниз, уравновешивается силами реакции опор (F_A) и (F_B), направленными вверх. begin{gather*} F_A+F_B=mg end{gather*} По правилу моментов при равновесии begin{gather*} F_Acdot OA=F_Bcdot OB=F_Bcdot 4OARightarrow F_A=4F_B \[7pt] F_A+F_B=5F_B=mgRightarrow F_B=frac{mg}{5} end{gather*} Получаем: begin{gather*} F_B=frac{500cdot 10}{5}=1000 text{Н}=1 text{кН}, F_A=4cdot 100=4000 text{Н}=4 text{кН} end{gather*} Ответ: 4 кН и 1 кН
п.7. Лабораторная работа №9. Проверка условия равновесия рычага
Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.
Теоретические сведения
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
Момент силы – это произведение силы, вращающей тело, на её плечо: (M=Fl).
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
begin{gather*} M_1=M_2\[7pt] F_1l_1=F_2l_2 end{gather*} |
В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ Delta l=frac D2=2 text{мм} $$
Для измерения веса груза используется динамометр с ценой деления $$ d=0,1 text{Н}. $$
Абсолютная погрешность определения веса $$ Delta_F=frac d2=0,05 text{Н}. $$
Относительные погрешности измерений: $$ delta_l=frac{Delta_l}{l}, delta_F=frac{Delta_F}{F}, delta_M=delta_l+delta_F $$
Абсолютная погрешность определения момента силы $$ Delta_M=Mcdot delta_M $$
Погрешности определения отношений сил и плечей: begin{gather*} r_F=frac{F_1}{F_2}, delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}, Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}\[7pt] r_l=frac{l_2}{l_1}, delta_{rF}=delta_{rl}frac{Delta_l}{l_1}+frac{Delta_l}{l_2}, Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl} end{gather*}
Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.
Ход работы
1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес (F_1).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил (M_1) и (M_2), их относительные и абсолютные погрешности.
7. Вычислите отношение сил (frac{F_1}{F_2}) и плеч (frac{l_2}{l_1}) для этого случая, погрешности их определения.
8. Сделайте выводы.
Результаты измерений и вычислений
| (F_1, text{Н}) | (l_1, text{см}) | (F_2, text{Н}) | (l_2, text{см}) | (F_1/F_2) | (l_2/l_1) |
| 2,9 | 5 | 1,0 | 15 | 2,9 | 3,0 |
Погрешности прямых измерений: $$ Delta_l=2 text{мм}=0,2 text{см}, Delta_F=0,05 text{Н} $$ Найдем моменты сил и погрешности вычислений: begin{gather*} M_1=F_1cdot l_1=2,9cdot 5=14,5 (text{Н}cdot text{м})\[7pt] delta_{M1}=frac{Delta_l}{l_1}+frac{Delta_F}{F_1}=frac{0,2}{5}+frac{0,05}{2,9}approx 0,04+0,017=0,057=5,7text{%} \[7pt] Delta_{M1}=M_1cdot delta_{M1}=14,5cdot 0,057approx 0,8 (text{Н}cdot text{м})\[7pt] M_1=(14,5pm 0,8) text{Н}cdot text{м}\[7pt] \[7pt] M_2=F_2cdot l_2=1,0cdot 15=15,0 (text{Н}cdot text{м})\[7pt] delta_{M2}=frac{Delta_l}{l_2}+frac{Delta_F}{F_2}=frac{0,2}{15}+frac{0,05}{1,0}approx 0,013+0,05=0,063=6,3 text{%} \[7pt] Delta_{M2}=M_2cdot delta_{M2}=15,0cdot 0,063approx 0,9 (text{Н}cdot text{м})\[7pt] M_2=(15,0pm 0,9) text{Н}cdot text{м} end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$
Погрешность вычислений для (frac{F_1}{F_2}) begin{gather*} delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}=frac{0,05}{2,9}+frac{0,05}{1,0}approx 0,017+0,05=0,067=6,7text{%}\[7pt] Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}=2,9cdot 0,067approx 0,2\[7pt] frac{F_1}{F_2}=2,9pm 0,2 end{gather*}
Погрешность вычислений для (frac{l_2}{l_1}) begin{gather*} delta_{rl}=frac{Delta_l}{l_1}+frac{Delta_l}{l_2}=frac{0,2}{5}+frac{0,2}{15}approx 0,04+0,013=0,053=5,3text{%}\[7pt] Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl}=3,0cdot 0,053approx 0,2\[7pt] frac{l_2}{l_1}=3,0pm 0,2 end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ frac{F_2}{F_2}=frac{l_2}{l_1} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5pm 0,8) text{Н}cdot text{м}, M_2=(15,0pm 0,9) text{Н}cdot text{м} $$ Таким образом, с учетом вычисленных погрешностей, (M_1=M_2) — правило моментов выполняется.
Отношения сил и плечей равны begin{gather*} frac{F_1}{F_2}=2,9pm 0,2, frac{l_2}{l_1}=3,0pm 0,2 end{gather*}
Таким образом, с учетом вычисленных погрешностей (frac{F_1}{F_2}=frac{l_2}{l_1}) — правило отношений выполняется.
Эксперименты подтвердили условие равновесия рычага.
Определять уравновешивающую силу или момент методом Н.Е. Жуковского можно в случаях, когда требуется найти только неизвестную внешнюю силу без определения реакций в кинематических парах, не прибегая к последовательному силовому расчету всего механизма.
Метод основан на принципе возможных перемещений – если система находится в равновесии, то сумма работ внешних сил и моментов на малых возможных перемещениях равна нулю (∑Ai = 0). Так как с помощью сил инерции (по принципу Даламбера) механизм приведен в состояние равновесия, то в данном случае принцип возможных перемещений применим.
Перейдем к конкретному мгновенному положению механизма, разделив все члены на бесконечно малый промежуток времени (dt), за который происходят указанные малые перемещения:
Таким образом, уравнение работ трансформируется в уравнение мгновенных мощностей и принцип возможных перемещений в применении к механизму можно сформулировать следующим образом – если механизм находится в равновесии, то сумма мгновенных мощностей всех внешних сил и моментов, приложенных к звеньям механизма, равна нулю.
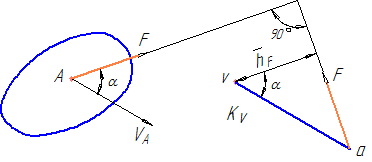
Жуковским Н.Е. был предложен метод составления этого уравнения с использованием плана скоростей (рисунок 19).
Рисунок 19
На рисунке 19 изображено некоторое звено, в точке А которого приложена сила F. Скорость VA этой точки изображается на плане скоростей вектором va в масштабе KV.
Перенесем силу F в точку «а» плана скоростей, повернув на 90° (в любую сторону). Возьмем формально момент этой повернутой силы относительно полюса плана скоростей:
В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.
Таким образом для составления уравнения Жуковского прикладывают все силы, действующие на звенья механизма (включая силы инерции), в соответствующие точки плана скоростей, предварительно повернув их на 90°. Взяв формально сумму моментов этих повернутых сил относительно полюса плана скоростей, фактически получают уравнение развиваемых ими мощностей.
К полученному уравнению добавляют мощности, развиваемые моментами (включая моменты сил инерции).
В уравнение Жуковского мощности должны входить с соответствующими знаками (см. рисунок 16 ). В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.
Примечание: для составления уравнения Жуковского можно на повернутый (на 90°) план скоростей прикладывать силы в своем истинном направлении.
Учет трения в механизмах >
Курсовой проект по ТММ >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Согласно принципу
возможных перемещений сумма элементарных
работ всех сил и моментов, приложенных
к системе, находящейся
в равновесии, на возможных перемещениях
системы равна нулю
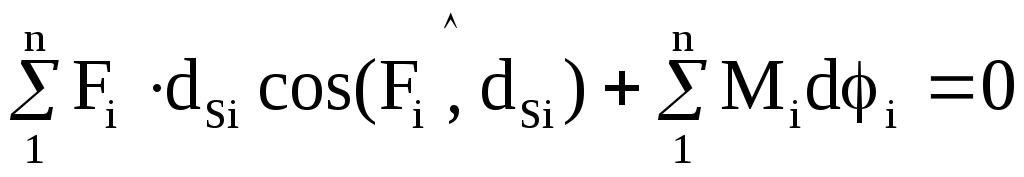
Для механизма
возможными перемещениями звеньев и
точек приложения сил будут их действительные
перемещения, являющиеся функциями
положения начального звена. Если
приложить к звеньям механизма силы
инерции, то можно рассматривать его в
состоянии динамического равновесия.
Так как силы,
действующие в кинематических парах,
являются внутренними, то уравнение
(2.118) позволяет найти величину
уравновешивающего момента или
уравновешивающей силы без их
предварительного определения.
Записанное выше
уравнение (2.118) неудобно для практического
использования, поэтому возьмем сумму
элементарных работ в единицу времени;
тогда, принимая во внимание, что
и
,
получим

где суммирование
проводится по всем
силам и
моментам сил всех звеньев механизма, а
каждое слагаемое представляет собой
мощность силы или момента.
Так как скорости
точек приложения сил и угловые скорости
звеньев известны по величине и направлению
из кинематического расчета, то единственным
неизвестным является искомая величина
уравновешивающего момента (или
уравновешивающей силы).
Для
кривошипно-ползунного механизма,
схема которого представлена на рис.
2.21, уравнение (2.119) запишется

Углы между
направлениями векторов сил и скоростей
можно взять из плана механизма (рис.
2.21). На рис. 2.21 показан только один из
углов –
.
Так как направление приложенного
уравновешивающего момента
взято на схеме механизма произвольно,
то при отрицательном значении
его направление следует изменить на
противоположное.
Для механизма с
гидроцилиндром, схема которого
приведена на рис. 2.22, уравнение (2.119)
будет иметь вид
(2.121)
Углы между
направлениями сил и скоростей, а также
знак уравновешивающей силы определяется
аналогично предыдущему примеру. На рис.
2.22 показан лишь угол между векторами
и
.
Основной смысл
применения принципа возможных перемещений
заключается в определении уравновешивающего
момента или уравновешивающей силы без
проведения силового анализа механизма
(без определения сил в кинематических
парах). Метод используют, как правило,
для проверки силового расчета.
2.4.5.Рычаг Жуковского
Графоаналитическое
решение уравнения (2.119) предложил Н.Е.
Жуковский в виде рычага Жуковского.
Пусть к звену
в точке
(рис. 2.23, а) приложена сила
любой природы.
— вектор абсолютной скорости точки
приложения силы
.
Угол
есть угол
.
Повернем вектор
скорости
в любую сторону на 90° и в конец повернутого
вектора скорости перенесем параллельно
самому себе вектор силы
(
и
на рис. 2.23, а).
а)
Тогда
.
Так как
и
,
то
. (2.122)
Здесь
— момент силы
относительно точки
— точки начала вектора абсолютной
скорости
.
Если
на звено действует момент сил
(рис. 2.23, б),то его можно представить
парой сил
,
и все сказанное выше относится и к силам
.
Если учесть, что
начало векторов абсолютных скоростей
всех точек располагается в полюсе плана
скоростей механизма, то теорему Жуковского
можно сформулировать следующим образом.
Если векторы всех
сил, приложенных к различным точкам
звеньев механизма, перенести параллельно
самим себе в одноименные точки повернутого
на 90° плана скоростей, приняв фигуру
плана за жесткий рычаг, то момент каждой
силы относительно полюса плана скоростей
будет пропорционален ее мощности, а
сумма моментов всех указанных сил будет
равна нулю.
При этом все
моменты, в том числе и уравновешивающий
момент, должны быть заменены парами
сил. Пара сил
,
заменяющая уравновешивающий момент,
равна
.
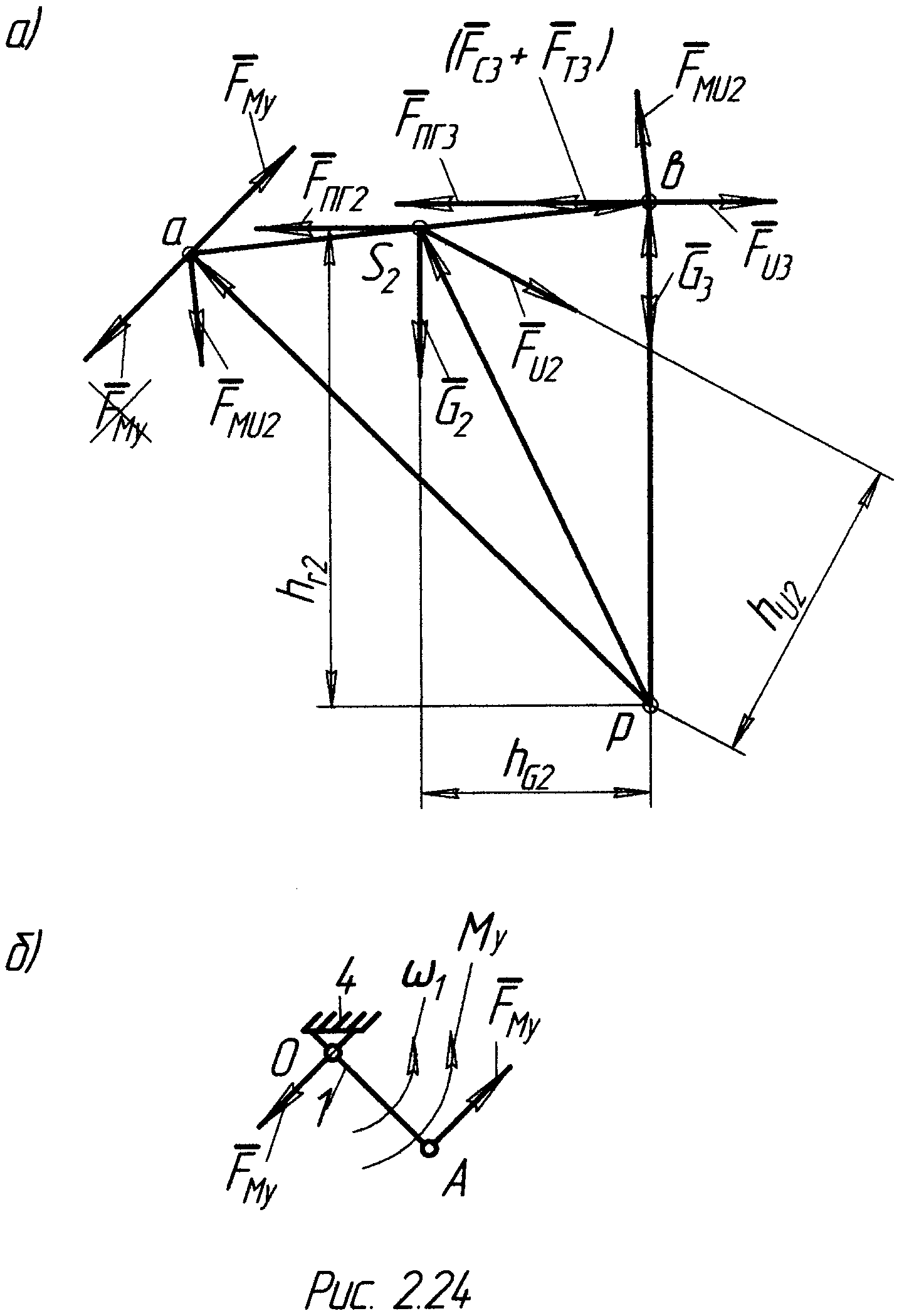
Рычаг Жуковского,
построенный для кривошипно-ползунного
механизма, изображенного на рис. 2.19,
а, представлен на рис. 2.24, а. План
скоростей
(рис. 2.9, б) повернут на 90°
против часовой стрелки. Сила
произвольно направлена вниз от точки
а плана.
Сумма моментов
сил относительно полюса р рычага
Жуковского имеет вид
.
Или
(2.123)
Отсюда
(2.124)
В этом выражении
плечи сил определяются из рычага
Жуковского путем их замера.
Как видно из
формулы, величина силы
не зависит от масштаба построения рычага
Жуковского.
Если расчет даст
отрицательное значение силы
,
то направление силы на рычаге Жуковского
следует сменить на противоположное.
Для определения
уравновешивающего момента необходимо
полученную силу перенести параллельно
самой себе из рычага Жуковского в точку
А первичного механизма (рис. 2.24, б), и
тогда уравновешивающий момент будет
положительным, и иметь вид:
.
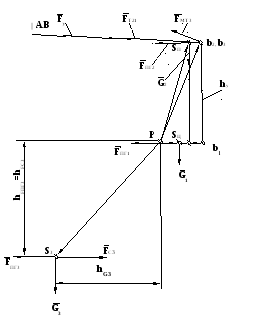
Рычаг Жуковского
для механизма с гидроцилиндром
(рис. 2.20, а) представлен на рис. 2.25.
Уравновешивающая сила
определяется из уравнения
.
Или
(2.125)
Отсюда
(2.126)
Рис.2.25
Рис. 2.25
Для определения
знака уравновешивающей силы необходимо
вектор
перенести параллельно самому себе из
рычага Жуковского на ось гидроцилиндра
механизма. Если направление силы
совпадёт с положительным направлением
скорости
,
то и сила
будет также положительной, в противном
случае сила
будет отрицательной.
Для механизма,
изображенного на рис. 2.20, а, уравновешивающая
сила Fy
положительна.
Вопросы для
самоконтроля.
-
Какова особенность
проведения силового анализа механизмов
с гидроцилиндром? -
Как определить
знак уравновешивающей силы в гидрорычажных
механизмах? -
Как определяется
масштабный коэффициент плана сил? -
В чём состоит
смысл применения принципа возможных
перемещений? -
Как формулируется
принцип возможных перемещений? -
Чему равна
мощность силы и момента сил? -
Как читается
теорема Жуковского о жестком рычаге в
силовом расчёте? -
Какое условие
является необходимым для использования
рычага Жуковского в силовом расчёте? -
Как определяется
уравновешивающая сила или уравновешивающий
момент при применении рычага Жуковского? -
С какой целью
определяют уравновешивающую силу или
уравновешивающий момент?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Теория пар сил
- Силы, направленные в одну сторону
- Силы направлены в противоположные стороны и различные по модулю
- Пара сил и ее момент
- Эквивалентность пары сил
- Добавление пар сил
- Условия равновесия пар сил
- Момент силы относительно точки на оси. Момент пары сил
- Момент силы относительно точки
- Теорема о моменте равнодействующей системы сходящихся сил
- Момент сил относительно оси
- Момент пары сил и его свойства
Парой сил называется система двух равных по модулю, противоположных по направлению параллельных сил.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Теория пар сил
Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы.
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны. Пара сил не составляет системы сил, эквивалентной нулю. Пару сил нельзя заменить одной силой, и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.
Пара сил, действующая на твердое тело, характеризуется, прежде всего, плоскостью действия. Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.
Силы, направленные в одну сторону
Пусть в абсолютно твердого тела в точках А и В приложены две параллельные силы




Поскольку 








Итак,
Силы 

действия имеют точку пересечения А. Перенесем силы 

Сила — скользящий вектор, поэтому 




Получим:
Поскольку силы 








Найдем точку приложения равнодействующей 



Поскольку

Итак, равнодействующая двух параллельных сил, направленных в одну сторону, параллельна этих сил, направленная в ту же сторону, что и составляющие силы; модуль
равнодействующей равна сумме модулей составляющих сил, а линия ее действия разделяет расстояние между точками приложения этих сил внутри на части, обратно
пропорциональны величинам этих сил.
Из изложенного следует, что произвольную силу можно разложить на две параллельные силы. Если 
Силы направлены в противоположные стороны и различные по модулю
Пусть параллельные силы 



Найдем равнодействующую сил 








Согласно (4.3), 
Поскольку 




Равнодействующая двух параллельных, разных по модулю, противоположно направленных сил параллельная им и направлена в сторону большей силы; модуль равнодействующей равна разности модулей составляющих сил. Линия действия равнодействующей 
Пара сил и ее момент
Система двух равных по модулю, параллельных, противоположно направленных сил, линии действия которых не совпадают, называется парой сил.
Пусть к некоторому абсолютно твердого тела приложена пара сил 
Согласно определению пары сил:
Элементами пары есть силы, составляющие пару, плечо пары, плоскость действия пары.
Плечо пары — это кратчайшее расстояние между линиями действия сил пары, то есть длина перпендикуляра h, опущенного из любой точки линии действия одной из сил пары на линию действия второй силы (рис. 4.3, а). Поскольку сила -скользящий вектор, то силы в паре всегда можно разместить так, чтобы расстояние АВ между точками их приложения было плечом пары (Рис. 4.3, б).
Плоскость действия пары — это плоскость, в которой размещены силы пара. Она единственная, поскольку через две параллельные линии можно провести только одну
плоскость.
Как будет показано в § 5.3, пара сил не имеет равнодействующей.
Пара сил не является системой уравновешенных сил, ибо в первой аксиомой статики две равные по модулю и противоположны по направлению силы будут уравновешенной системой сил только тогда, когда имеют общую линию действия. Силы, составляющих пару, не имеют общей линии действия.
Пара сил, действующая на тело, пытается вращать его. По мере вращательного действия силы в статике, как известно, является момент. Следовательно, и действие пары сил на тело должна характеризоваться моментом. Докажем это с помощью следующей теоремы.
Теорема 4.1. Векторная сумма моментов сил пары относительно произвольного центра
(Точки) в пространстве является величиной постоянной для данной пары.
Доказательство. Пусть задано пару сил
действие пары на тело характеризуется вращательным эффектом, найдем сумму моментов сил пары относительно центра О, произвольно расположенного в пространстве.
Получим:
где 


Здесь 


Известно, что вектор 


Аналогично, учитывая, что 
где вектор 


Следовательно, сумма моментов сил пары относительно произвольного центра в пространстве не зависит от выбора этого центра и равен моменту одной из сил пары относительно точки приложения другой силы. Теорема доказана.
Эта сумма моментов характеризует вращательное действие пары сил на тело. Назовем ее вектор-моментом пары сил. Обозначим вектор-момент пары сил 


С доказательства теоремы следует, что момент пары сил является вектором. Определим его величину и направление.
Величина момента пары по формулам (4.10) — (4.14) равна произведения величины одной из сил пары на плечо пары:
Вектор-момент пары сил направляется перпендикулярно к плоскости действия пары так, чтобы с его конца было видно попытки пары сил вращать тело против часовой стрелки (рис. 4.4).
Если на тело действует система пары сил, расположенных в одной плоскости, то вектор-моменты всех пар сил системы перпендикулярны этой плоскости. Итак, вектор-моменты такой системы пар является системой параллельных векторов, для составления которых достаточно знать их величины и знаки. Поэтому целесообразно ввести понятие алгебраического момента пары сил.
Алгебраическим моментом пары сил называется взятый со знаком «+» или «-» произведение одной из сил пары на плечо пары:
Алгебраический момент пары сил считаем положительным, если пара сил пытается вращать тело против часовой стрелки (рис. 4.5, а) и отрицательным, если пара сил пытается вращать тело по часовой стрелке (рис. 4.5, б). Алгебраические моменты пар сил на рисунках показывают дуговыми стрелками.
Эквивалентность пары сил
Рассмотрим теоремы, из которых вытекают основные свойства пары сил, которые предоставят нам возможность выполнять определенные действия над ними.
Теорема 4.2. Действие пары сил на тело не изменится при произвольном переносе этой пары в плоскости ее действия.
Доказательство. Пусть к некоторому телу приложена пара сил 


Силы выбираем так, чтобы
Согласно второй аксиомой статики
Перенесем силы 





Учитывая формулы (4.7) и (4.17), получим
Поскольку фигура 

и 











Это означает согласно формуле (4.18), заданной паре сил 

Покажем, что величина и направление векторов-моментов пар сил 


Из рис. 4.8 видно, что знак момента 



Теорема 4.3. Действие пары сил на твердое тело не изменится, если перенести эту пару в плоскость, параллельную плоскости ее действия.
Доказательство. Пусть на некоторое твердое тело действует пара сил 

Выберем в теле плоскость 



Приложим к телу в точках С и D две системы уравновешенных сил 

Проведем отрезки АС и ВD, точкой пересечения которых есть точка А.
Поскольку 

Добавим попарно силы 





Равнодействующая силы 

стороны. Итак, система сил 
и можно записать
Сравнивая соотношения (4.21) и (4.22), получим 


Вектор-моменты





Теорема доказана.
Теорема 4.4. Действие пары на тело не изменится, если изменить силы и плечо пары, оставляя неизменным ее вектор-момент.
Доказательство. Пусть к телу приложена пара сил 
Приложим к телу в точках А и В две силы 

За аксиомой параллелограмма сил найдем равнодействующие систем сил 

Учитывая, что 

Итак, 


силы

Плечо новой пары 


видно, что поскольку 







Из доказанных теорем следует:
1) пары эквивалентны, если равны их векторы-моменты;
2) вектор-момент пары сил является вектором свободным. Это означает, что его можно приложить в произвольной точке твердого тела.
Сформулированы три теоремы можно объединить в одну теорему: пары сил являются эквивалентными, если равны их векторы-моменты.
Из всего сказанного можно сделать вывод, что вектор-момент пары сил является полной характеристикой статическому воздействию пары на твердое тело. Поэтому действия над парами сил можно заменить эквивалентными операциями над их векторами-моментами.
Добавление пар сил
1. Геометрическое определение момента результирующей пары сил
Установим правило сложения пар сил, лежащих в плоскостях, которые пересекаются. Это правило вытекает из следующей теоремы.
Теорема 4.5. Две пары сил, которые лежат в плоскостях, пересекающихся эквивалентны одной паре, вектор-момент которой равен геометрической сумме векторов-моментов данных пар.
Доказательство. Пусть пары сил

Пользуясь теоремой 4.4, приведем обе пары к плечу АВ, размещенного на линии пересечения плоскостей П1 и П2 , то есть
При этом должны выполняться равенства

Добавим согласно аксиоме параллелограмма силы, приложенные в точках А и В. Получим 







Теорема доказана.
Аналогично можно добавить n пар сил в пространстве. В результате получим одну пару сил, вектор-момент которой равен векторной сумме векторивмоментив составляющих пар сил, а именно:
2. Аналитическое определение момента результирующей пары сил
Спроектируем равенство (4.25) на оси прямоугольной декартовой системы координат и используем теорему о проекции суммарного вектора на ось. Получим проекции момента результирующей пары сил на оси координат:
где 


и-й пары на оси выбранной системы координат.
Тогда величина вектора момента пары
а направление его найдем по формулам:
Известно (§ 4.2), что вектор-моменты пар, размещенных в одной плоскости, есть коллинеарными и поэтому добавляются алгебраически. Итак, момент результирующей
пары плоской системы пар равна сумме алгебраических моментов составляющих пар
Условия равновесия пар сил
1. Геометрическое условие равновесия пространственной системы пар сил
Пусть на тело действует n пар сил, произвольно расположенных в пространстве, вектори-моменты которых равны
В § 4.4 было доказано, что такая система пар сил эквивалентна одной паре сил, вектор-момент которой определяется формулой (4.25). очевидно, что тело под действием системы пар сил остается в равновесии, если вектор-момент результирующей пары будет равняться нулю
Это условие равновесия, учитывая формулу (4.25), запишем в виде
Формула (4.29) является геометрической условием равновесия пространственной системы пар, которую можно сформулировать так: пространственная система пар сил будет
находиться в равновесии тогда и только тогда, когда вектор-момент результирующей пары или геометрическая сумма векторов-моментов составляющих пар будет равняться нулю.
2. Аналитические условия равновесия пространственной системы пар сил
Из условия (4.29), учитывая формулу (4.26), получаем, что в случае равновесия пространственной системы пар сил то есть
Формулы (4.30) являются аналитическими условиями равновесия пространственной системы пар сил, которые формулируются так: пространственная система пар сил будет
находиться в равновесии тогда и только тогда, когда алгебраические суммы проекций
векторов-моментов составляющих пар на три взаимно перпендикулярные оси координат будут равны нулю.
3. Условие равновесия плоской системы пар сил
Условие равновесия плоской системы пар сил получаем из равенства (4.28).
Плоская система пар сил будет находиться в равновесии тогда и только тогда, когда сумма алгебраических моментов составляющих пар сил будет равняться нулю:
Условие равновесия плоской системы пар можно получить также из условий равновесия (4.30).
Действительно, пусть система пар сил размещена в координатной плоскости 



Поскольку 

Момент силы относительно точки на оси. Момент пары сил
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны, приложенных к телу в двух разных точках.
Момент силы относительно точки
Моментом силы 





Модуль этого векторного произведения:

Опустим перпендикуляр из точки 





Итак, момент силы относительно центра 
плечо, и направленный перпендикулярно к плоскости, проходящей через точку 


Очевидно, момент силы относительно точки имеет все свойства векторного произведения. Из формулы (2.1) можно найти проекции вектора 

Раскрывая этот определитель по элементам первой строки и раскладывая вектор 



Сравнивая левую и правую части равенства (2.5), имеем

Модуль, и направление момента силы относительно точки можно определить еще и так:
Заметим, что формулы (2.6) легко получить, пользуясь правилом циклической
перестановки индексов.
По определению момента силы относительно точки имеем:
1) если переместить силу вдоль линии ее действия, то момент силы относительно точки не изменится;
2) момент силы относительно точки всегда равен нулю, когда линия действия силы проходит через эту точку (в этом случае плече 
3) момент силы относительно точки численно равен удвоенной площади треугольника 

Теорема о моменте равнодействующей системы сходящихся сил
Теорема Вариньона. Момент равнодействующей сходящейся системы сил относительно произвольного центра равен векторной (геометрической) сумме моментов составляющих сил относительно того самого центра:

Доказательство. Пусть в точке А пересекаются линии действия системы сходящихся сил




получим:

что и требовалось доказать.
Если силы и точка О размещены в одной плоскости, то их моменты перпендикулярны этой плоскости и лежат на одной прямой. Поэтому момент равнодействующей такой системы сил равен алгебраической сумме моментов составляющих сил относительно этой
точки.
Момент сил относительно оси
Моментом силы относительно оси называется проекция на эту ось момента силы относительно любой точки, лежащей на этой оси (рис. 2.5).
Из этого определения следует, что моменты сил относительно координатных осей вычисляются по формулам (2.6). Эти формулы, в частности, показывают, что момент силы
относительно оси не зависит от выбора точки на оси.
При решении конкретных задач моменты сил относительно осей удобно вычислять более наглядным способом (рис. 2.6) по следующему правилу.
1. Проводим произвольную плоскость 

пересечения этой плоскости с осью.
2. Проектируем силу 
3. Вычисляем момент проекции 

При этом момент силы относительно оси считается положительным, если наблюдатель видит со стороны положительного направления оси 


Как видно из рис. 2.6, численное значение момента силы относительно оси 

Из определения момента силы относительно оси следует, что он равен нулю, если линия действия силы и ось лежат в одной плоскости.
Пример 1. Сила 
с осью 





Вычислить момент этой силы относительно оси
Решение.
По формулам (2.6), есть


Известно, что 
или
Если 

Если 

Момент пары сил и его свойства
Парой сил называется система двух равных по величине сил 


Определим, чему равна сумма моментов сил, составляющих пар относительно произвольной точки.
Пусть О — произвольная точка пространства (Рис. 2.7, б), a 


Полученная векторная сумма не зависит от положение точки 
Векторное произведение


плечо пары.
Как видим, момент пары направленный перпендикулярно к плоскости действия пары в ту
сторону, откуда «вращение» пары происходит против часовой стрелки.
Итак, момент пары сил — вектор свободный и математически определен в виде

Ниже показано, что момент пары полностью определяет статическое действие пары сил на твердое тело, то есть полной характеристикой механического воздействия пары сил на это тело. Из определения момента пары сил и аксиомы I о двух силах следует, что пара сил является уравновешенной системой (система сил, эквивалентная нулю) тогда и только тогда, когда момент пары равна нулю. Другие свойства пары сил определяются следующими теоремами.
Теорема 1. Не меняя действия пары сил на твердое тело, его можно переносить и произвольно вращать в плоскости действия, изменяя величину силы, входящей в нее, и длину плеча так, чтобы момент пары оставался неизменным.
Доказательство. Пусть задано пару сил



на линиях, перпендикулярные к нему, приложим соответственно две системы сил







Перенесем теперь силы 



















Покажем, что при указанном перемещении пары сил можно изменять величину
силы, входящей в нее, и длину плеча, о чем говорится в теореме. Для этого рассмотрим исходную пару сил 
Приложим к точкам а и b систему сил 

равнодействующие сходящихся систему сил










Теорема 2. Две пары сил, которые лежат в одной или параллельных плоскостях и имеют одинаковые по величине, но противоположные по направлению моменты, составляют систему пар сил, эквивалентную нулю.
Доказательство. Пусть в плоскости заданы две пары сил 







С другой стороны, сумма моментов всех сил, которые составляют эти пары, определяется выражением:

которое является суммой моментов составляющих пар, равных нулю. Следовательно, эта система двух пар сил эквивалентна нулю.
Поскольку момент пары сил — вектор свободный, то доказанные теоремы справедливы также для случая пар сил, лежащих в параллельных плоскостях.
Из доказанных теорем следует вывод об эквивалентности двух пар сил, имеющих геометрически одинаковые моменты.
Кроме того, эти теоремы позволяют установить правило составления пар сил, которые лежат не только в параллельных плоскостях, но и в тех, которые пересекаются.
Так, если задан систему n пар 



Отметим, что пару сил нельзя заменить одной силой, которая была бы эквивалентна по действию на твердое тело двум равным по величиной, параллельным и противоположно направленным силам. Действительно, если предположить, что пара сил эквивалентна некоторой силе 



Итак, пара сил, действующих на твердое тело, образует новый самостоятельный элемент статики, который вместе с силой составляет важное понятия механики. Основные свойства этого элемента и основные преобразования, которым он подлежит, вполне устанавливаются доказанными теоремами о парах.
Эти свойства и превращения будут выглядеть так:
1) пару сил можно переносить в плоскости ее действия, в том числе и вращать на любой угол;
2) пару сил можно переносить в любую плоскость, параллельную плоскости действия этой пары;
3) можно изменять силы, образующие пару и плечо, не меняя момента пары;
4) несколько пар сил, произвольно расположенных в пространстве, можно заменить одной парой, момент которой равен геометрической сумме моментов составляющих пар.
Из изложенного в главах 1 и 2 приходим к такому важному выводу: механическое влияние в статике характеризуется тремя типами векторов: силой — скользящим вектором, моментом силы относительно точки — приложенным вектором и парой сил — свободным вектором.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Теоретическая механика представляет раздел физики, в котором изложены основные законы механических взаимодействий и движений материальных тел.
Понятие момента силы в теоретической механике
Определение 2
В теоретической механике говорится о таком понятии, как момент силы. Он представляет собой величину, характеризующую вращательную способность силы.
Парой сил считается система двух параллельных, противоположно направленных и равнозначных по модулю сил: $vec{F}$, $vec{F^2}$. Тело, под воздействием пары сил, будет совершать вращательные движения.
Системой сил является комплекс сил, оказывающих непосредственное воздействие на механическую систему. Плоскую систему при этом представляют силы, чьи линии действия лежат в одной плоскости. Пространственную систему – силы, у которых линии действия не лежат в одинаковой плоскости.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Систему сходящихся сил представляют силы, чьи линии действия будут пересекаться в одной точке. В произвольной системе линии действия сил не будут пересекаться в одной точке.
Равновесное состояние характеризует такое положение, тело при котором в момент действия сил или сохраняет неподвижность, или движется равномерным и прямолинейным образом.
Уравновешенной системой сил считается такая система, которая, прилагаясь к свободному твердому телу, сохраняет неизменность его механического состояния (то есть не выводит из равновесия). Равнодействующей силой будет та сила, чье воздействие на тело эквивалентно действиям системы сил.
Проекцию силы на ось представляет заключенный между перпендикулярами отрезок. При этом они проведены из начала и конца вектора силы к данной оси. Проекция положительная при совпадении направленности отрезка и положительного направления оси. Проекцию силы на плоскость представляет вектор на плоскости между перпендикулярами, которые проведены из начала и конца вектора силы к такой плоскости.
«Моменты в теоретической механике» 👇
Момент силы относительно оси
Замечание 1
Моментом силы относительно оси будет считаться момент проекции такой силы на перпендикулярную оси плоскость в отношении точки их пересечения.
Момент окажется положительным при условии, что поворот, совершаемый силой, осуществляется против часовой стрелки, и отрицательным – если против, записывается это формулой:
$M_z (vec{F} = M_0 (vec{F_xy}) = hF_xy$
Для нахождения момента силы относительно оси нужно:
- провести перпендикулярно оси $z$ плоскость и спроецировать на нее силу $F$;
- спроецировать силу $F$ на вышеуказанную плоскость с последующим вычислением величины проекции $F_xy$;
- провести $h$ (плечо) из точки, где пересекается ось с плоскостью, на линию действия проекции $F_xy$ с последующим определением его длины;
- вычислить произведение этого плеча, а также — проекции силы с соответствующим знаком.
Нулевое значение момент силы относительно оси обретает в том случае, когда $F_xy=0$ (при параллельности силы $F$ оси). Второе условие заключается в том, что линия действия силы будет пересекать ось, т.е. $h=0$.
Равнодействующую $R$ двух сходящихся сил находят по аксиоме параллелограмма сил. Геометрическую сумму любого числа сходящихся сил вычисляют посредством последовательного суммирования двух сил (способом векторного многоугольника).
Таким образом, систему сходящихся сил $vec{F_n}$ приводят к одной равнодействующей силе $vec{R}$
Аналитически равнодействующую силу определяют ее проекцией на оси координат:
$R=sqrt{R_x^2+R_y^2R_z^2}$
Исходя из теоремы, проекция равнодействующей на ось вычисляется формулой:
$R_x=F_1x+F_2x+F3x$
Или
$F_kx=sum{F_kx}$
С учетом этого, равнодействующую определяет выражение:
$R=sqrt{(sum{F_kx})^2+(sum{F_ky})^2+(sum{F_kz})^2}$
Действие системы для сходящихся сил будет эквивалентным действию одной равнодействующей силы. Условием равновесия тела считается нулевое значение равнодействующей, т.е. $vec{R}=0$
Из формулы $R=sqrt{(sum{F_kx})^2+(sum{F_ky})^2+(sum{F_kz})^2}$ следует, что главным и необходимым условием равновесного состояния пространственной системы сходящихся сил будет нулевое значение суммы проекций всех сил на оси $X$, $Y$, $Z$:
$sum{F_kx}=0$
$sum{F_ky}=0$
$sum{F_kz}=0$
Необходимым условием равновесия для плоской будет нулевое значение суммы проекций всех сил на оси $X$, $Y$:
$sum{F_kx}=0$
$sum{F_ky}=0$
Момент силы относительно точки
Абсолютное значение момента в теоретической механике вычисляется формулой:
$M_0(vec{F})=hF$
При положительном моменте сила вращает плечо $h$ против часовой стрелки, а при отрицательном – по часовой.
Согласно свойствам момента силы относительно точки, он сохраняет свою неизменность, если точка приложения силы переносится вдоль линии ее действия. Еще одно свойство проявляется в том, что момент равнодействующей силы относительно точки определяет сумма моментов слагаемых сил в отношении этой точки:
$M_0(vec{R})=M_0(vec{F_1})+M_0(vec{F_1})$,
где $vec{R}=vec{F_1}+vec{F_2}$
Момент пары сил
Момент пары сил определяет формула: $M(vec{F},vec{F})=Fh$где $vec{F},vec{F}) – силы, которые составляют пару, $h$ — плечо пары. — плечо пары.
Момент пары окажется положительным при стремлении сил к вращению плеча против часовой стрелки. Свойства пары сил выражены в: нулевом значении суммы проекций сил на ось; неизменности момента пары при одновременном изменении значения сил и плеча пары, возможности переноса пары в плоскости ее действия при неизменности действия пары на тело.
Момент силы относительно точки будет выражать следующая формула: $M_0(vec{F})=hF$. Момент окажется положительным при стремлении силы к вращению плеча против часовой стрелки и отрицательным – когда вращать будет по часовой.
Свойства момента силы в отношении точки выражаются в следующем: его неизменности в момент переноса точки приложения силы вдоль линии ее действия; момент равнодействующей силы в отношении точки представляет суммарное значение моментов слагаемых сил относительно нее: $M_0(vec{R})=M_0(vec{F_1})+M_0(vec{F_2})$, где $vec{R}=vec{F_1}+vec{F_2}$, нулевом значении момента силы при прохождении линии действия силы через точку ее приложения;
Приложенную к твердому телу силу возможно перенести. При этом будет неизменным оказываемое ею действие, а перенос осуществляется параллельно в другую точку тела. Также при этом добавляется пара сил с моментом, равнозначным переносимой силе относительно точки, куда она переносится. Вследствие вышеуказанного преобразования мы наблюдаем формирование сходящейся системы сил и суммы моментов пар сил. Действие такой системы заменяют действия суммарной силы, а действие моментов — суммарный момент.
Суммарный вектор $vec{R}$ считается главным вектором системы сил. Суммарный момент $M_0(vec{F_k})$ — основной момент системы сил.
Итогом становится тождественное преобразование произвольной системы сил в главный вектор и момент такой системы. Аналитически главный вектор и момент системы могут определяться их проекциями на оси координат:
$R=sqrt{sum{R_kx}^2+sum{R_ky}^2+sum{R_kz}^2}$
$M=sqrt{sum{M_kx}^2+sum{M_ky}^2+sum{M_kz}^2}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме