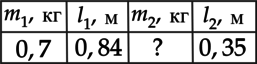Статика — раздел механики, изучающий условия равновесия тел.
Виды равновесия
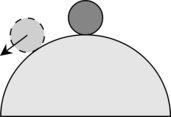
Устойчивое равновесие |
|
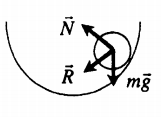 |
Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min). |
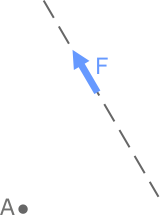
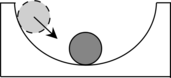
Неустойчивое равновесие |
|
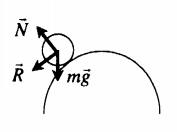 |
Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max). |
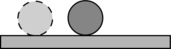
Безразличное равновесие |
|
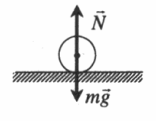 |
При выведении тела из положения безразличного равновесия дополнительных сил не возникает. |
Момент силы
Определение
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M = Fd
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
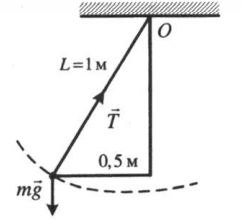
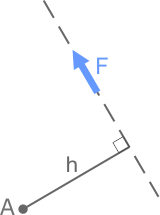
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)
Момент силы может быть положительным и отрицательным.
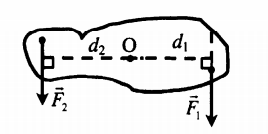
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
M1 = F1d1
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
M2 = F2d2
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
∑Mi=0
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑Mпо час. стр.=∑Mпр. час. стр.
Условия равновесия тел
| Тело не участвует в поступательном движении: |
∑→Fi=0; →vo=0 |
| Тело не участвует во вращательном движении: |
∑Mi=0; ω0=0 |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) |
∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0 |
Простые механизмы
Определение
Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
Наклонная плоскость |
|
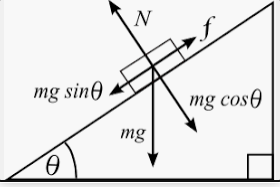 |
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg |
Рычаг |
|
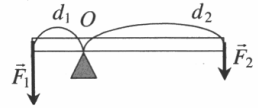 |
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1 |
Неподвижный блок |
|
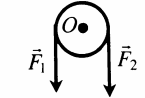 |
Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2 |
Подвижный блок |
|
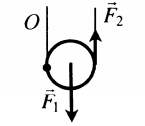 |
Дает выигрыш в силе в 2 раза:
d1 = R d2 = 2R F1 = 2F2 |
Клин |
|
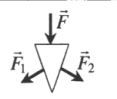 |
Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2 |
Золотое правило механики
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
Задание EF22660
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов и выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
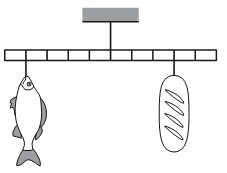
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2=0,8·0,30,4=0,6 (кг)
Ответ: 0,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18706
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Решение
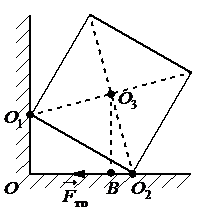
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 9.7k
Определение
Момент силы — это крутящий или вращательный момент, который является векторной величиной.
Чтобы определить, чему равен момент силы, нужно получить произведение вектора силы и радиус-вектора, который проводится к точке приложения силы от оси вращения. Поэтому величину можно назвать характеристикой вращательного воздействия силы на твердое тело.
Термины “крутящий” и “вращающий” моменты в данном случае не являются тождественными. Разница между ними состоит в том, что “вращающий” момент воспринимается как внешнее усилие, которое прикладывают к объекту. Термин “крутящий” же рассматривается как внутреннее усилие, которое появляется при приложении конкретных нагрузок (что делает определение схожим с используемым при изучении сопротивления материалов).
Понятие «момент силы»
Физики воспринимают этот термин в качестве так называемой “вращающей силы”. В соответствии с системой СИ, измеряется данная величина в ньютон-метрах. Иногда в литературе можно также встретить понятие “момент пары сил” (такое определение, например, появляется в исследованиях Архимеда над рычагами).
При использовании простых примеров (например, при приложении силы к рычагу в перпендикулярном отношении к нему) величина рассчитывается как произведение расстояния до оси вращения рычага и непосредственно силы, которая на него воздействует.
Пример: На рычаг оказывает воздействие силы в 3 ньютона, которую прикладывают на расстоянии 2 м от оси вращения рычага. В результате момент силы будет равнозначен силе в 1 ньютон, прикладываемой на расстоянии 6 м по отношению к рычагу.
Как определить, чему равен момент силы
Формула
Точно определить момент действия силы частицы удастся, применив следующую векторную формулу:
[vec{mathrm{M}}=vec{mathrm{r}} vec{mathrm{F}}]
В данном случае [vec{mathrm{r}}] — это радиус вектора частицы, а
[vec{mathrm{F}}] — сила, воздействующая на эту частицу.
Важно помнить, что в физике энергия воспринимается как скалярная величина. В то же время момент силы считается (псевдо)векторной величиной. Поэтому совпадение размерностей указанных величин никогда не бывает случайным. Например, момент силы в 1 Н/м, приложенный через целый оборот, при выполнении механической работы сообщает энергию в 2 Дж. В математическом отображении эта формула момента силы будет выглядеть так:
[mathbf{E}=mathbf{M} boldsymbol{theta}], где:
- [mathbf{E}] — это энергия;
- [mathbf{M}] — это вращающийся момент;
- [boldsymbol{theta}] — это угол в радианах.
В современных условиях момент силы измеряется при помощи особых датчиков нагрузки, которые могут быть трех типов:
- оптического;
- тензометрического;
- индуктивного.
Применение специальной техники позволяет определить величину предельно точно и избавляет ученых от необходимости производить лишние расчеты.
Нет времени решать самому?
Наши эксперты помогут!
Момент силы: формулы
Наиболее интересным в физике считается определение момента силы в поле. Для этого используется следующая формула:
[vec{M}=vec{M_{1}} vec{F}]
Где:
[vec{M_{1}}]- это момент рычага;
[vec{F}]- это величина силы, действующей на тело.
У такой формулы момента силы в физике будет один недостаток. С ее помощью не удастся определить, в каком направлении направлен момент силы. Известной станет только его величина. Если сила окажется перпендикулярной вектору, тогда момент рычага окажется равен расстоянию от центра до точки, в которой была приложена сила. В таком случае момент силы достигнет максимального значения:
[vec{T}=vec{r} quad vec{F}]
Если сила совершает какое-либо действие на определенном расстоянии, она параллельно выполняет механическую работу относительно того же объекта. В таком случае в физической практике считается, что и момент силы выполняет работу (при совершении действия через угловое расстояние).
[mathrm{P}=mathrm{M} {omega}]
Международная система измерений предлагает определять мощность в Ваттах, при этом момент силы измеряется в радианах в секунду. Для определения величину угловой скорости используется единица “радианы в секунду”).
Как определяется момент действия нескольких сил
Если на тело действуют одновременно две равные по величине и противоположно направленные силы (не лежащие на одной и той же прямой), оно находится в состоянии равновесия. Такая ситуация связана с тем, что результирующий момент данных сил по отношению к любой из осей не обладает нулевым значением. Ведь обе силы направлены в одну сторону момента и являются парой сил.
Если тело закреплено на оси, оно будет вращаться под влиянием пары сил. Когда же пара сил прилагается по отношению к свободному телу, последнее начнет крутиться вокруг той оси, которая проходит через центр тяжести.
В соответствии с правилом моментов сил в физике, момент пары сил считается одинаковым по отношению к любой оси, перпендикулярной плоскости этой пары. При этом суммарный момент пары M всегда определяется как произведение плеча пары (то есть расстояния l между силами) и одной из этих сил F. Данный расчет производится независимо от типов отрезков, на которые разделяется положение оси.
[mathrm{M}=mathrm{FL}_{1}+mathrm{FL}-2=mathrm{FL}_{1}+mathrm{L}_{2}=mathrm{FL}]
В случае, если равнодействующая момент нескольких сил равняется нулю, он будет одинаковым по отношению ко всем параллельным друг другу осям. Именно поэтому воздействие всех сил на тело можно заменить действием только одной пары сил, имеющих точно такой же момент.
Содержание:
- Определение и формула момента силы
- Момент силы относительно оси
- Главный момент сил
- Основной закон динамики вращательного движения
- Единицы измерения момента силы
- Примеры решения задач
Определение и формула момента силы
Определение
Векторное произведение радиус – вектора ($bar{r}$),
который проведен из точки О (рис.1) в точку к которой приложена сила
$bar{F}$ на сам вектор
$bar{F}$ называют моментом силы ($bar{M}$) по отношению к точке O:
$$bar{M}=bar{r} times bar{F}(1)$$
На рис.1 точка О и вектор силы (
$bar{F}$)и радиус – вектор
$bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы
($bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы
выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор
$bar{M}$ создают правовинтовую систему.
Направление момента сил и углового ускорения совпадают.
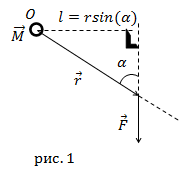
Величина вектора $bar{M}$ равна:
$$M=r F sin alpha=l F$$
где $alpha$ – угол между направлениями радиус – вектора и вектора силы,
$l=r sin alpha$– плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на
данную ось. При этом выбор точки значения не имеет.
Главный момент сил
Главным моментом совокупности сил относительно точки О называется вектор
$bar{M}$ (момент силы), который равен сумме моментов всех сил, действующих в системе по отношению
к той же точке:
$$bar{M}=sum_{i=1}^{k} bar{M}_{i}=sum_{i=1}^{k} bar{r}_{i} times bar{F}_{i}(3)$$
При этом точку О называют центром приведения системы сил.
Если имеются два главных моменты ($bar{M}$ и
$overline{M^{prime}}$)для одной системы сил для разных двух центров приведение сил (О и О’), то они связаны выражением:
$$bar{M}^{prime}=bar{M}-bar{r}_{O^{prime}} times bar{F}(4)$$
где $bar{r}_{O^{prime}}$ — радиус-вектор, который проведен из точки О к точке О’,
$bar{F}$ – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента
$bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$bar{M}=frac{d bar{L}}{d t}$$
где $bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$bar{M}=I bar{varepsilon}(6)$$
где I – момент инерции тела, $bar{varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
Пример
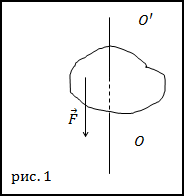
Задание. На рис.1 показано тело, которое имеет ось вращения OO’.
Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.
Решение. За основу решения задачи примем формулу, определяющую момент силы:
$$bar{M}=bar{r} times bar{F}(1.1)$$
В векторном произведении (видно из рисунка) $bar{r} neq 0, bar{F} neq 0$ . Угол между вектором силы и радиус –
вектором также будет отличен от нуля (или $180^{circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $bar{M} neq 0$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
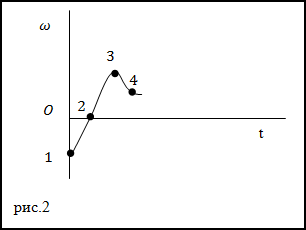
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2.
В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I varepsilon(2.1)$$
где $varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$varepsilon=frac{d omega}{d t}(2.2)$$
Перепишем (2.1), используя (2.2), имеем:
$$M=I frac{d omega}{d t}(2.3)$$
Так как $I neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
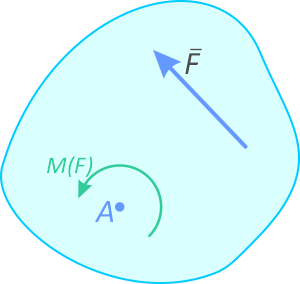
Моментом силы называют вращательное усилие создаваемое вектором силы относительно твердого тела, оси или точки.
Обозначение: M, m или M(F).
Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]
Аналогом момента силы является момент пары сил.
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.
Определение
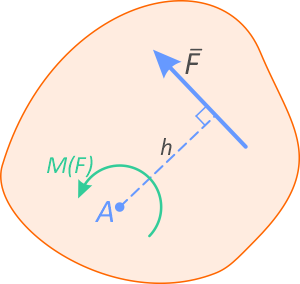
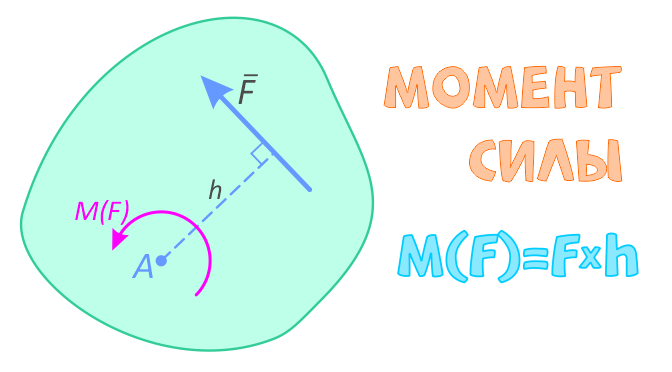
Момент определяется как произведение силы F на плечо h:
M(F)=F×h
Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.
Наш короткий видеоурок про момент силы с примерами:
Другие видео
Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки вращения создает момент M=7×0,35=2,45 кНм.
Пример момента силы
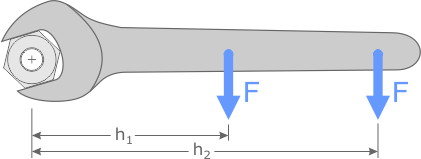
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.
Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.
Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h2>h1).
Плечом при этом служит расстояние от центра гайки до точки приложения силы.
Плечо момента силы
Рассмотрим порядок определения плеча h момента:
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.
Покажем линию действия силы F (штриховая линия)
Проведем из точки A перпендикуляр h к линии действия силы
Длина отрезка h есть плечо момента силы F относительно точки A.
Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).
Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.
Примеры расчета момента силы
Сила расположена перпендикулярно оси стержня
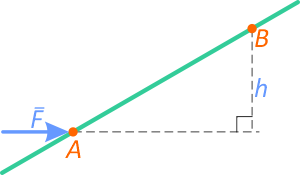
Если сила F приложена перпендикулярно к оси бруса и известно расстояние между точками A и B.
То момент силы F относительно точки A:
МA=F×AB
Сила расположена под углом к оси стержня
В случае, если сила F приложена под углом α к оси балки
Момент силы относительно точки B:
MB=F×cosα×AB
Известно расстояние от точки до линии действия силы
Если известно расстояние от точки где определяется момент до линии действия силы (плечо h)
Момент силы относительно точки B:
MB=F×h
См. также:
- Примеры решения задач >
- Момент силы относительно точки
- Момент силы относительно оси
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Момент силы, механическое равновесие тела
При одновременном действии на одно тело нескольких сил тело движется с ускорением.
Линия действия силы — прямая, проходящая через вектор силы. Если силы действуют параллельно друг другу, то точки приложения результирующей силы нет.
Момент силы относительно оси вращения — это произведение силы на плечо. [vec{M}=vec{F}vec{l}]
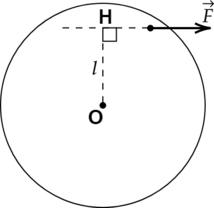
Плечо силы — это расстояние от оси вращения до линия действия силы. В качестве примера на рисунке изображён некий диск, к которому приложена сила (vec{F}). Ось вращения перпендикулярна плоскости чертежа и проходит через точку O. Плечом силы является величина (l = OH), где (displaystyle H) — основание перпендикуляра, опущенного из точки O на линию действия силы.
Момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил равна нулю.
Условия равновесия тела:
1) Силы уравновешены вдоль любой оси.
2) Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.
Также условия равновесия тела можно сформулировать следующим образом:
1) Равна нулю векторная сумма всех сил, приложенных к телу.
2) Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.
Центр тяжести тела — центр параллельных сил тяжести элементарных частей этого тела.
1) Если однородное тело имеет ось симметрии, то центр тяжести находится на этой оси.
2) Если однородное тело имеет плоскость симметрии, то центр тяжести находится в этой плоскости.
3) Если однородное тело имеет центр симметрии, то центр тяжести находится в этой точке.
Виды равновесия
Равновесие называется устойчивым, если после небольших внешних воздействий тело возвращается в исходное состояние равновесия.
Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия.
Равновесие называется безразличным, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил равна нулю.
Сила, приложенная к рычагу слева равна 300 Н. Какой длины должно быть ее плечо, чтобы рычаг находился в равновесии, если момент силы, действующей на него справа, равен 90 Н(cdot)м? (Ответ дайте в сантиметрах.)
Пусть (M_1) – момент силы, приложенной к рычагу справа, а (M_2) – слева. Чтобы рычаг находился в равновесии, моменты сил, действующих на него слева и справа, должны быть равны: [M_1 = M_2] В то же время момент силы (M_2) по определению равен произведению силы на ее плечо: [M_2 = Fcdot{l},] где (F) – величина силы, приложенной слева; (l) – длина плеча слева. Исходя из этого получаем, что: [M_1 = Fcdot{l}] Отсюда выразим (l): [l = frac{M_1}{F}] [l = frac{90text{ Н}cdot{text{м}}}{300text{ Н}} = 0,3text{ м} = 30text{ см }]
Ответ: 30
Тело массой 1 кг подвешено к правому плечу невесомого рычага (см. рисунок). К какому делению левого плеча рычага нужно подвесить груз массой 3,5 кг для достижения равновесия?
Пусть масса правого груза (m_1), а левого – (m_2).
Обозначим длину одного деления за (l). Тогда, исходя из рисунка, длина правого плеча равна (l_1 = 7l), а длина левого плеча равна (l_2 = nl), где (n) – количество делений.
Чтобы рычаг достиг равновесия, моменты сил, действующих на него справа и слева, должны быть равны: (M_1 = M_2).
В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] Отсюда получаем: (F_1l_1 = F_2l_2)
Выразим длину левого плеча рычага: (displaystyle{l_2 = frac{F_1l_1}{F_2}})
На оба груза действует единственная сила – сила тяжести, поэтому: [F_1 = m_1g] [F_2 = m_2g] С учетом этого: [l_2 = displaystyle{frac{m_1gcdot{l_1}}{m_2g}} = frac{m_1l_1}{m_2}] [displaystyle{l_2 = frac{1text{ кг}cdot{7l}}{3,5text{ кг}} = 2l}Rightarrow nl = 2l Rightarrow n = 2]
Ответ: 2
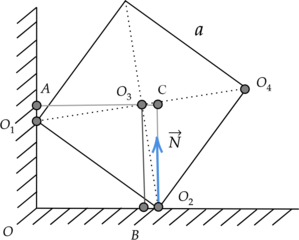
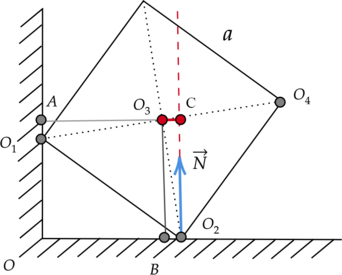
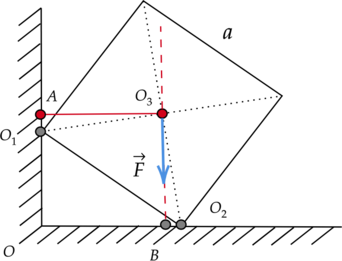
Две вершины однородного железного куба объемом (V = 512) см(^3) опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равно плечо силы реакции опоры относительно оси, перпендикулярной плоскости чертежа и проходящей через точку (O_3)? (O_2C = sqrt{7}) см (Ответ дайте в метрах.)
Плечо – это кратчайшее расстояние между осью вращения и линией действия силы. Мысленно продолжим линию действия силы реакции опоры (N) и перпендикуляром соединим ее с прямой, проходящей через точку (O_3). Получаем, что плечом этой силы является отрезок (O_3C).
Воспользуемся геометрией, чтобы найти отрезок (O_3C).
Рассмотрим треугольник (Delta O_1O_2O_4) с прямым углом (O_2): [O_1O_4^2 = O_1O_2^2 + O_4O_2^2] [O_1O_2 = O_2O_4 = a] [displaystyle{O_1O_4 = sqrt{2a^2} = asqrt{2}}] Далее найдем отрезок (O_2O_3): [displaystyle{O_2O_3 = frac{1}{2}O_1O_4} = frac{asqrt{2}}{2}] Рассмотрим треугольник (Delta O_3O_2C) с прямым углом (C): [O_3O_2^2 = O_3C^2 + O_2C^2] [displaystyle{O_3C = {sqrt{O_3O_2^2 — O_2C^2 }}}] [displaystyle{O_3C = {sqrt{left(frac{asqrt{2}}{2}right)^2 — O_2C^2 }}}] Зная объем куба, можно найти его сторону (a): [V = a^3 Rightarrow a = sqrt[3]{V} = sqrt[3]{512text{ см}^3} = 8 text{ см }] Тогда: [displaystyle{O_3C = {sqrt{left(frac{8text{ см}cdotsqrt{2}}{2}right)^2 — (sqrt{7}text{ см})^2 }} = 5 text{ см} = 0,05text{ м }}]
Ответ: 0,05
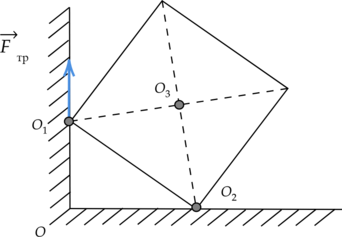
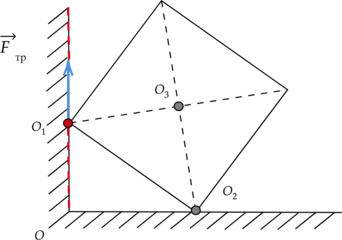
Две вершины однородного медного куба опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равен момент силы трения относительно оси, проходящей через точку (O_1) перпендикулярно плоскости рисунка, если масса куба равна 0,7 кг? (OO_2 = 0,4) м (Ответ дайте в Н(cdot)м)
Момент силы трения (M) равен произведению модуля силы трения (F_text{тр}) на ее плечо (l): [M = F_text{тр}cdot{l}] Прямая (OO_1) – линия действия силы трения. По рисунку видно, что длина плеча силы трения (l) относительно точки (O_1) равна нулю (так как ось вращения, проходящая через точку (O_1), перпендикулярна линии действия силы трения).
Следовательно, и момент силы трения (M) так же равен нулю: [M = F_text{тр}cdot{0}text{ м} = 0text{ Н}cdot{text{м }}]
Ответ: 0
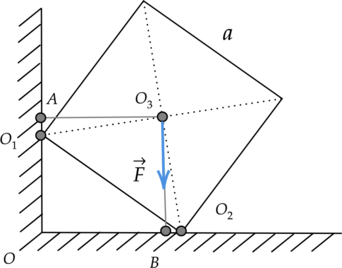
Две вершины однородного деревянного куба со стороной (a = 5sqrt{2}) м опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равен момент силы тяжести относительно оси, перпендикулярной плоскости чертежа и проходящей через точку (A)? (AO_1 = 3) м (Ответ дайте в МН(cdot)м и округлите до десятых.)
Момент силы тяжести M равен произведению модуля силы тяжести (F) на ее плечо (l): [M = Fcdot{l}] Плечо – это кратчайшее расстояние между осью вращения и линией действия силы. Мысленно продолжим линию действия силы тяжести (F) и перпендикуляром соединим ее с прямой, проходящей через точку (A). Получаем, что плечом силы тяжести является отрезок (AO_3).
Воспользуемся геометрией, чтобы найти отрезок (AO_3).
Рассмотрим треугольник (Delta O_1O_2O_3) с прямым углом (O_3): [O_1O_2^2 = O_1O_3^2 + O_2O_3^2] [O_1O_3 = O_2O_3] [O_1O_2^2 = 2O_1O_3^2] [displaystyle{O_1O_3 = frac{O_1O_2}{sqrt{2}}}] [displaystyle{O_1O_3 = frac{5sqrt{2}}{sqrt{2}}} = 5text{ м }] Рассмотрим треугольник (Delta O_1AO_3) с прямым углом A: [O_1O_3^2 = AO_3^2 + AO_1^2] [AO_3 = sqrt{O_1O_3^2 — AO_1^2}] [AO_3 = sqrt{(5text{ м})^2 — (3text{ м})^2} = 4text{ м }] Сила тяжести равна произведению массы куба (m) на ускорение свободного падения (g): [F = mg] Подставим это значение в исходную формулу: [M = mgcdot{AO_3}] Зная плотность и объем куба, можно найти его массу: [displaystyle{rho =frac{m}{V}},text{ где }V = a^3] [m = rho V = rho a^3] Подставим это значение в предыдущую формулу и найдем искомую величину: [M = rho a^3gcdot{AO_3}] [displaystyle{M = 400text{ }frac{text{кг}}{text{м}^3}cdot{(5sqrt{2}text{ м})}^3cdot{10frac{text{м}}{text{с}^2}}cdot{4}text{ м} approx 5,7text{ М,Н$cdot$м }}]
Ответ: 5,7
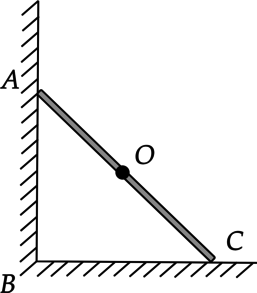
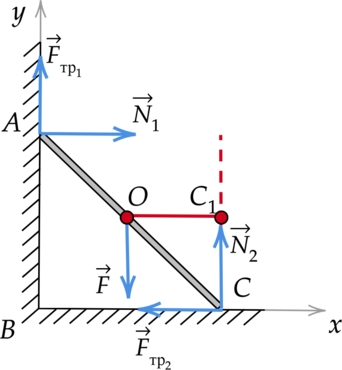
На прут массой 1 кг со стороны вертикальной поверхности действует сила трения, равная 3 Н. Найдите момент силы реакции опоры, действующей на него со стороны горизонтальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, если (AB = 6,5) м, а (AC = 9,7) м. (Ответ дайте в Н(cdot)м и округлите до целого числа.)
Момент действующей на горизонтальную стенку силы реакции опоры относительно оси, перпендикулярной плоскости рисунка и проходящей через точку (O), равен: [M = N_2l,] где (l) – плечо силы. Мысленно продолжим линию действия силы рекции опоры (N_2) и перпендикуляром соединим ее с прямой, проходящей через точку (O). Получаем, что плечом силы (N_2) является отрезок (OC_1), равный: [displaystyle{OC_1 = frac{BC}{2}} = frac{sqrt{AC^2 — AB^2}}{2}] [OC_1 = frac{sqrt{9,7text{ м}^2 — 6,5text{ м}^2}}{2} = 3,6text{ м }] Чтобы найти неизвестную величину (N_2), укажем все силы, действующие на прут, и запишем второй закон Ньютона с учетом того, что тело находится в равновесии: [vec{F}_{text{тр}1} + vec{N}_1 + vec{F} + vec{N}_2 + vec{F}_{text{тр}2} = 0] Введем оси (OX) и (OY), спроецируем на них все силы. [OX: N_1 — F_{text{тр}2} = 0] [OY: F_{text{тр}1} + N_2 — F = 0] Выразим силу реакции опоры (N_2), действующую на горизонтальную стенку: [N_2 = F — F_{text{тр}1}] Сила тяжести (F) по определению равна: (F = mg), поэтому: [N_2 = mg — F_{text{тр}1}] [N_2 = 1text{ кг}cdot{10text{ }frac{text{м}}{text{c}}^2} — 3text{ H} = 7text{ H }] Подставим найденные значения в начальную формулу: [M = 7{text{ Н}cdot{3,6}text{ м}} = 25,2text{ Н}cdot{text{м}}approx{25}text{ Н}cdot{text{м }}]
Ответ: 25
Группа школьников проводила лабораторную работу, исследуя основные условия равновесия легкого рычага, плечи сил которого равны (l_1) и (l_2). К рычагу с двух сторон ребята подвесили грузы массой (m_1) и (m_2).
Результаты эксперимента были занесены в следующую таблицу:
Чему равна масса груза (m_2), если рычаг находился в равновесии? (Ответ дайте в килограммах и округлите до десятых.)
Так как рычаг находился в равновесии, то моменты сил, действующих на него справа и слева, должны быть равны: (M_1 = M_2).
В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] Отсюда получаем: (F_1l_1 = F_2l_2)
На оба груза действует единственная сила – сила тяжести, поэтому: [F_1 = m_1g] [F_2 = m_2g] С учетом этого: (M_1 = m_1gcdot{l_1}) и (M_2 = m_2gcdot{l_2}). Приравняв (M_1) и (M_2), получаем, что: [m_1gcdot{l_1} = m_2gcdot{l_2}] [m_1l_1 = m_2l_2] Выразим массу второго груза (m_2): [displaystyle{m_2 = frac{m_1l_1}{l_2}}] [displaystyle{m_2 = frac{0,7text{ кг}cdot{0,84text{ м}}}{0,35text{ м}}} approx 1,7text{ кг }]
Ответ: 1,7

УСТАЛ? Просто отдохни