Некоторые приложения тройного интеграла
Объем тела
Объем области 
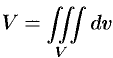
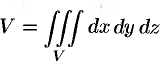
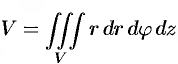
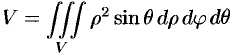
Масса тела
Масса тела 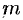
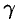
где 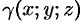
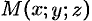
Статические моменты
Моменты 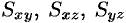
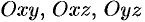
Центр тяжести тела
Координаты центра тяжести тела 
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
а моменты инерции относительно координатных осей:
Пример №54.4.
Найти объем тела, ограниченного поверхностями 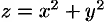
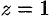
Решение:
Данное тело ограничено сверху плоскостью 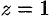
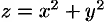
Пример №54.5.
Найти массу шара 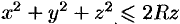
Решение:
Уравнение сферы 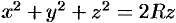
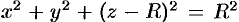
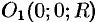
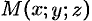
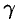
где 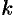
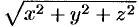

Итак,
Вычислять интеграл будем в сферических координатах. Уравнение сферы 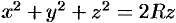

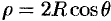
Поэтому сферические координаты будут изменяться в следующих пределах: 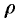
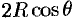
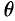
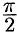
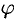
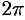
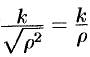
Из соображений симметрии следует, что 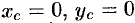
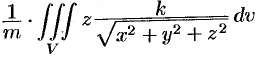
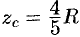
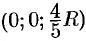
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
fitta |
Заголовок сообщения: Найти момент инерции тела относительно оси Oz
|
||
|
Найти момент инерции тела, ограниченного поверхностями x[math]^{2}[/math][math]+[/math] y[math]^{2}[/math][math]=[/math] z[math]^{2}[/math], z [math]= h[/math] относительно оси Oz. Помогите пожалуйста решением.
|
||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти момент инерции тела относительно оси Oz
в форуме Интегральное исчисление |
Stavatar |
2 |
324 |
19 май 2019, 16:40 |
|
Найти момент инерции относительно оси Oz
в форуме Интегральное исчисление |
Yyurqa |
6 |
1162 |
12 дек 2013, 15:01 |
|
Найти момент инерции относительно оси Oz
в форуме Интегральное исчисление |
Metrirkh |
1 |
276 |
28 апр 2021, 18:02 |
|
Момент инерции относительно оси OY
в форуме Интегральное исчисление |
Sup_4eg |
1 |
536 |
01 апр 2017, 14:20 |
|
Определить момент инерции относительно оси
в форуме Интегральное исчисление |
math1love |
2 |
153 |
20 янв 2020, 20:23 |
|
Найти момент инерции тела относительноотносительно оси z
в форуме Интегральное исчисление |
elektron4ik |
5 |
328 |
28 апр 2017, 19:08 |
|
Объем тела и момент инерции однородного тела. Интегралы
в форуме Интегральное исчисление |
barabshka |
1 |
104 |
30 май 2022, 13:56 |
|
Момент инерции твердого тела
в форуме Механика |
Finn_parnichka |
1 |
245 |
28 янв 2018, 17:50 |
|
Вычислить момент инерции однородного тела
в форуме Интегральное исчисление |
Zed |
2 |
506 |
18 окт 2015, 17:41 |
|
Найти момент инерции
в форуме Интегральное исчисление |
S77R |
1 |
1146 |
28 янв 2014, 07:23 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: Yandex [bot] и гости: 5 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
I Вычисление объёмов тел
.
Пример
1. Вычислить
объём тела, ограниченного поверхностями
,
,
.
Решение.
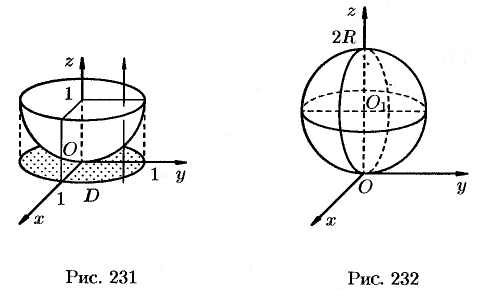
Тело, представляет собой полушар с
конической выемкой. Проекция на плоскость
– круг радиуса
с центром в начале координат, следовательно,
координатаССК изменяется от 0 до
.
Проекция на плоскость– полукруг с вырезанным сектором
(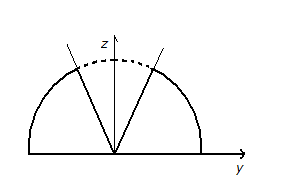
конусаэтой плоскостью – это
).
Координатаизменяется от
на образующих конуса до
на плоскости
.
И, наконец, координата.
Итак, объём тела
Здесь повторный
интеграл представляет собой произведение
трех интегралов, ибо внутренние интегралы
не зависят от внешних переменных.
II Вычисление масс тел
где
– плотность распределения массы.
Пример
2. Найти
массу шара
если плотность в каждой точке
пропорциональна расстоянию от
до некоторой фиксированной точки
поверхности шара.
Решение.
Поместим фиксированную точку в начало
координат, а центр шара на ось
.
Тогда уравнение сферы в сферических
координатах имеет вид (см. §6, замечание
3):,
.
Далее, плотность,.
Имеем для массы:
III Вычисление координат центра масс тела
Формулы для
координат центра масс тела выводятся
так же как аналогичные формулы для
плоской фигуры. Не будем выводить их, а
просто приведем:
П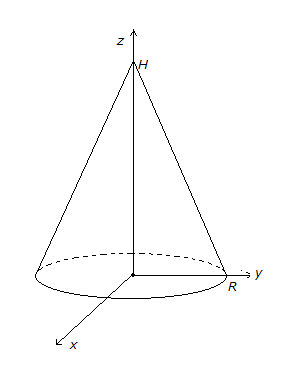
3. Найти
положение центра масс однородного
конуса с радиусом основания
и высотой
.
Решение.
Расположим конус обычным образом:
основание в плоскости
,
вершина на оси.
Выясним какие поверхности ограничивают
это тело. Одна из них – это плоскость,
а вторая – это нижняя часть конической
поверхности,
смещенная вверх наН.
Имеем:
Коэффициент
найдем из того усло-вия, что пересечение
этой поверхности с плоскостью– круг радиусаR:
.
Итак, задачу можно
сформулировать так: «Найти координаты
центра масс тела, ограниченного
поверхностями
и
,
если
».
Тело симметрично относительно оси
и в симметричных точках плотность
одинакова. Следовательно, центр масс
лежит на оси:
Итак, центр масс
однородного конуса расположен на его
оси на расстоянии четверти высоты от
основания.
IV Вычисление моментов инерции тела
Формулы для
всевозможных моментов инерции тела
аналогичны подобным формулам для плоской
фигуры.
Моменты инерции
относительно осей координат:
Моменты инерции
относительно координатных плоскостей:
Момент инерции
относительно начала координат:
Пример
4. Найти
момент инерции цилиндра
относительно фиксированной образующей,
если плотность в каждой его точке обратно
пропорциональна расстоянию от точки
до этой образующей.
Р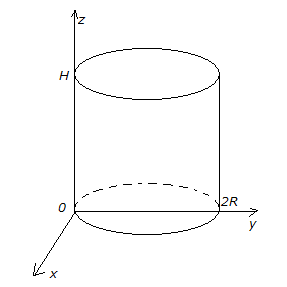
Пусть образующая, о которой говорится
в условии задачи, лежит на оси
,
а центр нижнего основания на оси.
Цилиндр ограничен поверхностями
Цилиндрическое
уравнение третьей поверхности:
.
Плотность
в силу условия
Итак, момент инерции:
V Вычисление силы притяжения точки телом
Пусть в точке А
находится
масса
,
а в точкеВ
– масса М.
Известно, что М
притягивает
(и наоборот) с силой
такой, что
,
где).
Пусть теперь эти
точки находятся в системе координат:
Проекции
силы
вычисляются по формулам
Но
поэтому, например,
где
Аналогичные формулы есть для
и
.
Итак, проекции силы:
Пусть теперь тело
имеет плотность
.
Как найти силу,
с которой телопритягивает массу
,
находящуюся в точке?
Можно поступить обычным, при построении
приложений интеграла, способом. Всю
областьразбиваем на части
,
выбираем точкии считаем, что вся масса
сосредоточена в
.
Получим системуматериальных точек:
с массой
.
(Подобным образом мы поступали при
вычислении координат центра масс и
моментов инерции плоской фигуры. Так
же можно поступить и при нахождении
этих характеристик пространственной
области.)
Точка
притягивает
с силой
,
где, например,
вычисляются
аналогично. Суммируя и переходя к
пределу, получим для проекций полной
силы
:
где
Пример 5.
Найти силу, с которой однородный конус
притягивает массу
,
находящегося в его вершине.
Решение.
Впишем данный конус в систему координат
так, как показано на рисунке. Такой конус
можно описать как тело, ограниченное
поверхностями
и
(смотри пример 3).
В силу симметрии
и однородности
сила притяжения направлена по оси
.
Имеем:
.
Переходим к
цилиндрическим координатам. Полярные
координаты проекции произвольной точки
тела на плоскость
изменяются в пределах
,
а координатаизменяется от конуса до плоскости, т.е.
отдо
.
Итак,
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 12.01.2014 Сообщений: 13 |
|
|
1 |
|
Найти момент инерции тела, ограниченного поверхностями21.06.2014, 13:15. Показов 8260. Ответов 2
Найти момент инерции относительно оси Oz однородного тела, ограниченного поверхностями:
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
21.06.2014, 13:15 |
|
Ответы с готовыми решениями: Найти момент инерции относительно Oz тела, ограниченного поверхностями
Найти объем тела, ограниченного поверхностями Найти объем тела, ограниченного поверхностями 2 |
|
137 / 137 / 21 Регистрация: 03.07.2012 Сообщений: 293 |
|
|
23.06.2014, 17:05 |
2 |
|
Во-первых, надо построить эти поверхности (см. рис), Миниатюры
0 |
|
137 / 137 / 21 Регистрация: 03.07.2012 Сообщений: 293 |
|
|
23.06.2014, 17:27 |
3 |
|
В цилиндрических координатах:
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
23.06.2014, 17:27 |
|
Помогаю со студенческими работами здесь
Найти объем тела, ограниченного поверхностями
Найти объем тела, ограниченного поверхностями Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 3 |
Приложения кратных интегралов в механике
Краткая теория
Масса и статистические моменты пластики
Если
– область плоскости
, занятая пластинкой, и
– поверхностная плотность пластики в точке
, то масса
пластинки и ее статистические моменты
и
относительно осей
и
выражаются двойными интегралами:
Если
пластика однородна, то
Координаты центра тяжести пластики
Если
– центр тяжести пластики, то
где
– масса пластинки и
– ее статистические моменты относительно осей
координат.
Моменты инерции пластики
Моменты
инерции пластинки относительно осей
и
соответственно равны:
Момент инерции пластики относительно
начала координат:
Полагая
, получаем геометрические моменты инерции плоской
фигуры.
Масса тела, занимающего область
![]() и статистические моменты тела относительно
и статистические моменты тела относительно
координатных плоскостей
где
– плоскость тела в точке
Координаты центра тяжести
Если тело
однородно, то формулах для координат центра тяжести можно положить
.
Моменты инерции относительно
осей координат
Полагая в
этих формулах
, получаем геометрические
моменты инерции тела.
Примеры решения задач
Задача 1
Вычислить
массу материальной пластины, занимающей область
плоскости
, если поверхностная
плотность
и границы области
заданы уравнениями.
Решение
Сделаем
чертеж области
:
Искомая
масса материальной пластины:
Ответ:
Задача 2
Найти
статистический момент фигуры, ограниченной линиями
и
относительно оси абсцисс.
Решение
Сделаем
чертеж:
Статистический
момент относительно оси
:
Ответ:
Задача 3
Вычислить
координаты центра масс однородной
материальной пластины
, ограниченной данными
линиями:
Решение
Сделаем
чертеж:
Масса
пластинки:
Статистические
моменты:
Искомые
координаты центра масс:
Ответ:
.
Задача 4
Вычислить массу тела
, ограниченного заданными поверхностями
-плотность в
точке
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Изобразим
тело на рисунке:
С боков
тело будет ограничено цилиндром
и плоскостями
. Сверху плоскостью
Проекция на плоскость
:
Ответ:
Задача 5
Найти
момент инерции однородного шара
с массой
относительно оси
.
Решение
Момент
инерции относительно оси
можно найти по формуле:
Шар
однородный, поэтому плотность:
Перейдем
к сферическим координатам:
Получаем:
Ответ:


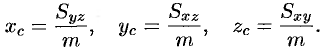
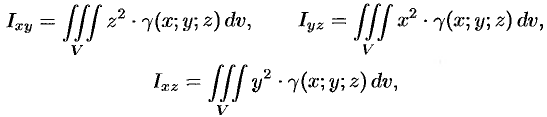
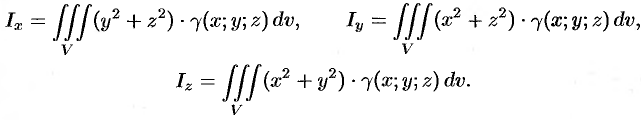
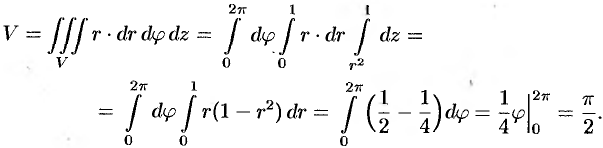
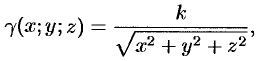
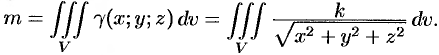
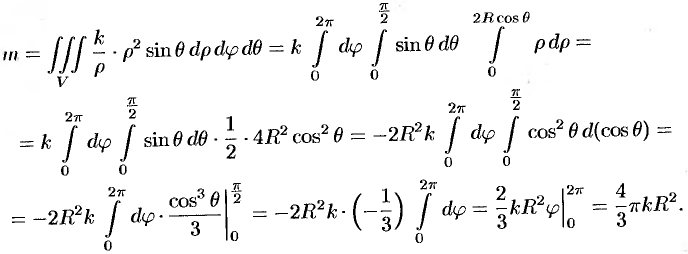









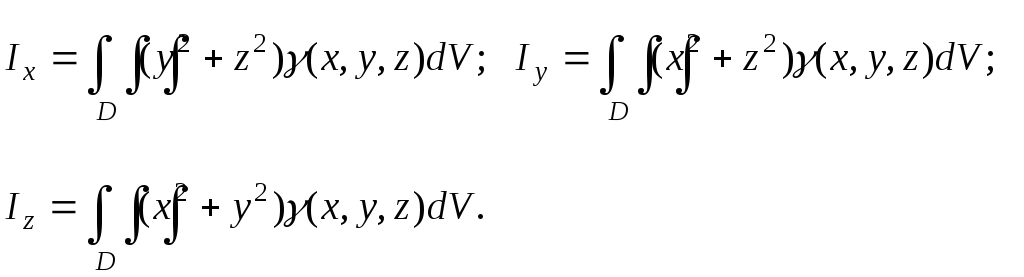




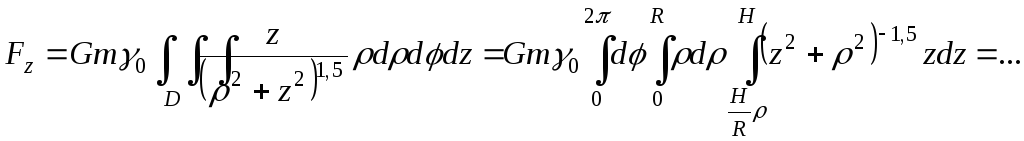

 Определить момент инерции относительно оси Oz тела, ограниченного поверхностями?
Определить момент инерции относительно оси Oz тела, ограниченного поверхностями?