Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
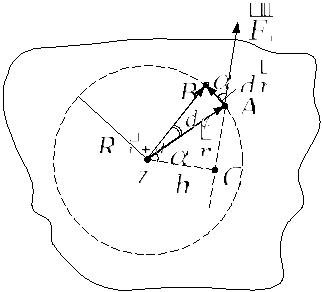
Во всех четырех случаях мы рассматривали
моменты инерции тела относительно оси,
проходящей через центр инерции этих
тел. С помощью теоремы Штейнера можно
найти моменты инерции тел относительно
других произвольных осей, что бывает
необходимо, ибо вращение не всегда
бывает относительно центра инерции.
Теорема Штейнера:
Момент инерции тела относительно
произвольной оси равен сумме его момента
инерции относительно оси, проходящей
через центр масс и параллельно данной,
и произведения массы тела на квадрат
расстояния между осями
(—
расстояние между осямиzиc).
Доказательство:
|
|
Рассмотрим |
(по определению)
Видно, что
(по определению)
(т.к.

Таким образом,
§14. Основное уравнение динамики вращательного движения
Пусть к твердому телу с неподвижной
осью вращения в некоторой точке
приложена сила
.
|
|
Тогда если точка А совершает элементарное
Представим силу |
Тогда элементарная работа
.
Точка
,
как и все точки тела, движется по
окружности, плоскость которой
перпендикулярна осиz, а
значитсоединяет две точки этой окружности и
также лежит в плоскости, перпендикулярной
осиz, а значит и вектору,
т.е..
Следовательно,,
где
—
угол между векторамии
.
Рассмотрим вид сверху.
|
|
В силу того, что
Вектор
|
,
где
.
Опр.
Величина
,
равная расстоянию от линии, вдоль которой
действует сила, до оси вращения, называется
плечом силы.
Опр.
Величина произведения проекции силы
на плоскость вращения ()
и плеча силыназывается моментом силы относительно
оси вращенияz.
Если сила
,
приложенная к телу, приводит к увеличению
угла поворота (т.е. к вращению тела по
выбранному положительному направлению
вращения), то момент такой силы является
величиной положительной. Если же сила
приводит к уменьшению угла, то момент
силы отрицателен. Исходя из того, что
величина элементарной работы равна,
то, согласно теореме о кинетической
энергии (),
приравнивая правые части уравнений
получим:
(Т.к.
и
)
Это и есть основной закон динамики
вращательного движения.
Формулировка закона:
Момент силы относительно оси вращения
равен произведению момента инерции
относительно этой оси и углового
ускорения.
Легко можно показать, что если на тело,
закрепленное вокруг оси вращения,
действует множество сил с различными
моментами, то алгебраическая сумма
моментов сил относительно оси вращения
равна произведению момента инерции
относительно этой оси и углового
ускорения:
§15. Момент импульса.
Закон сохранения
момента импульса
|
Поступательное |
Вращательное движение |
|
m |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
Продолжая аналогию |
|
|
|
|
-момент
импульса вращающегося вокруг осиzтела.
Продолжим аналогию еще далее, поставив
вопрос, а обладает ли момент импульса
свойством сохранения.
Действительно
=>
=>
,
Видно, если
,
то
Таким образом, если алгебраическая сума
моментов всех сил, приложенных к телу,
относительно оси вращения равна 0, то
момент импульса относительно этой оси
есть величина постоянная.
Легко доказать, что таким же образом
сохраняется момент импульса системы
тел, вращающихся вокруг данной оси с
различными угловыми скоростями
,
а не одного только твердого тела.
Закон сохранения момента импульса:
Момент импульса замкнутой системы тел
относительно произвольной оси есть
величина постоянная.
В заключении рассмотрим частные случаи
в решении задач при определении момента
импульса тела, размерами которого, по
сравнению с расстоянием до оси вращения,
можно пренебречь.
1. Материальная точка вращается по
окружности.
2. Если точечное тело движется в
произвольном направлении относительно
оси вращения.
|
|
где |
Соседние файлы в папке Лекции
- #
- #
- #
Моменты инерции тел
Инерционные свойства твердого тела характеризуются не только его массой 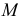
Моментом инерции тела относительно оси называется сумма произведений массы каждой точки на квадрат расстояния от точки до оси
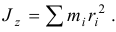
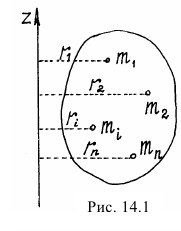
Заметим сразу, что момент инерции тела — это геометрическая характеристика тела, не зависящая от его движения (рис. 14.1).
Для однородных тел простой симметричной формы момент инерции можно найти в справочниках. А моменты инерции некоторых тел, которые чаще всего встречаются при исследовании движения материальных систем, даны на рис. 14.2.
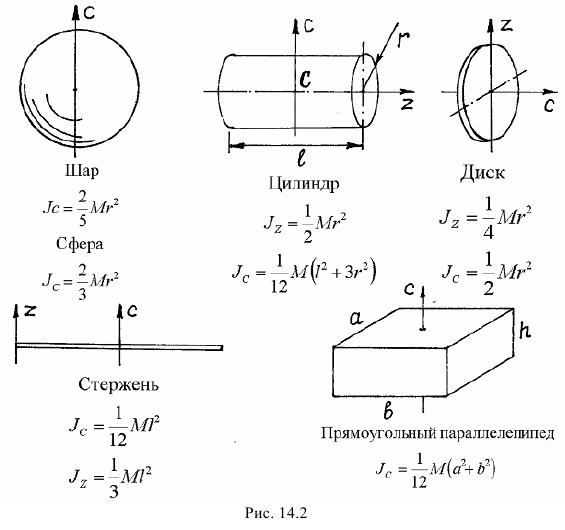
На рисунке даны моменты инерции тел относительно осей симметрии. Но нередко при исследовании движения реальных механизмов приходится определять моменты инерции относительно осей, не совпадающих с осями симметрии. Этому помогают следующие теоремы.
Теорема Гюйгенса-Штейнера о моментах инерции тела относительно параллельных осей
Найдем зависимость между моментами инерции тела относительно параллельных осей 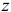
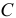
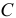
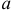
По определению (14.3)
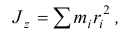
причем
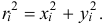
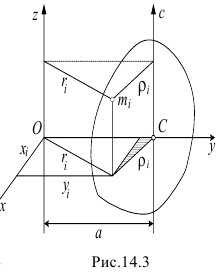
Но из заштрихованного прямоугольного треугольника (см. рис. 14.3) следует, что
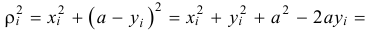
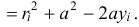
Значит
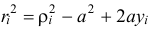
и момент инерции относительно оси
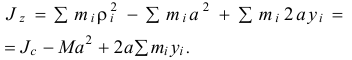
Но по формуле (14.2) сумма
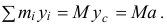
Поэтому
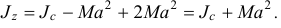
Следовательно, момент инерции тела относительно оси 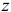
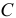
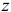
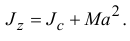
Так, например, момент инерции стержня относительно оси
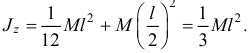
А момент инерции прямоугольного параллелепипеда относительно оси 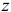
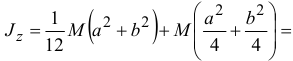
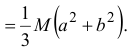
Момент инерции тела относительно произвольной оси
Найдем момент инерции тела относительно оси 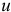
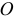
По определению момент инерции
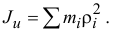
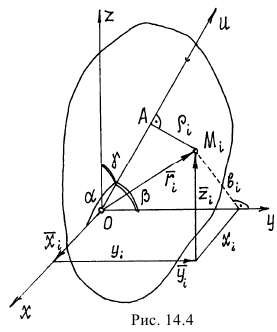
Поместим в точку 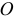
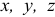
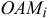
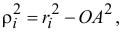
где
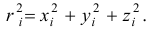
И так как радиус-вектор точки 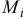
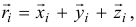
то, проектируя это равенство на ось 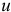
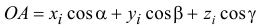
Как известно из тригонометрии
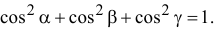
Поэтому
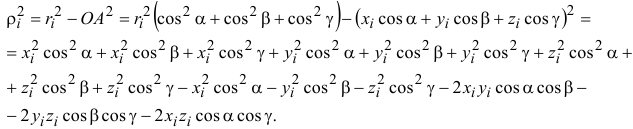
И, группируя подобные члены, содержащие косинусы одинаковых углов,
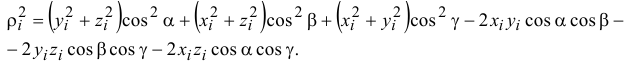
Но
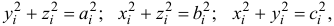
где
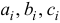
расстояние от точки 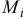
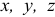
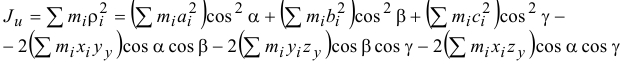
или
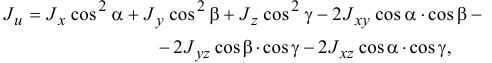
где 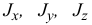

Если два центробежных момента инерции, оба содержащих в индексах названия какой-нибудь одной оси, равны нулю, то эта ось называется
главной осью инерции. Например, если 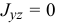
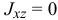
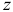
Так как все моменты инерции зависят от того, где находится точка 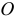
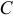
Если в данной точке координатные оси являются главными осями инерции (центробежные моменты инерции относительно их равны нулю), то формула (14.5) упрощается
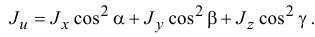
Иногда по некоторым признакам нетрудно найти главные оси инерции тела.
- Если у однородного тела имеется ось симметрии, то эта ось является главной центральной осью инерции.
Действительно. Направим координатную ось 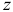
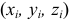
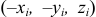
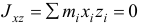
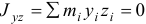
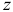
- Если у однородного тела имеется плоскость симметрии, то любая ось, перпендикулярная ей, будет главной осью инерции для всех точек этой плоскости.
Направим ось 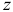
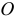
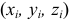
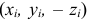
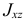
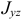
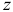
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы: