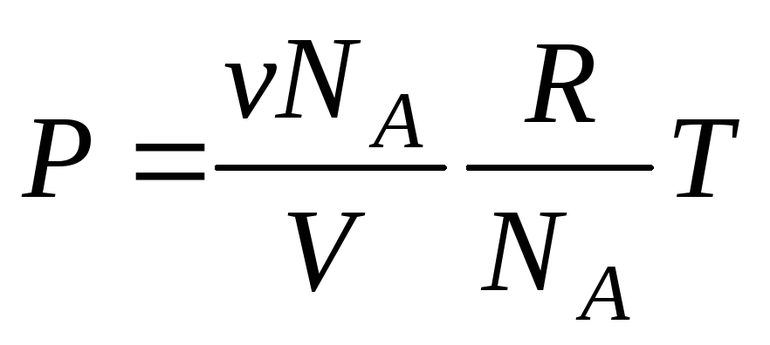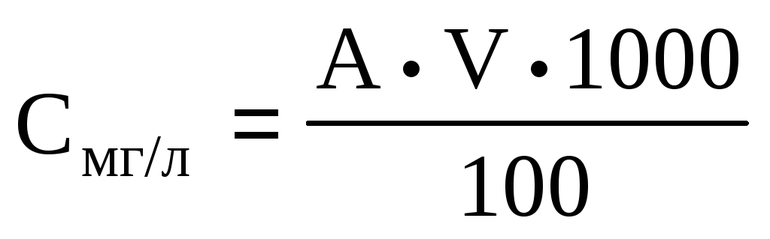Раствор
–
гомогенная (однородная) система, состоящая
как минимум из двух компонентов, один
из которых растворитель, другой –
растворенное вещество. То есть состав
раствора = растворитель + растворенное
вещество.
Например,
водный раствор хлорида натрия состоит
из двух компонентов: воды (растворителя)
и хлорида натрия (растворенного вещества).
Существует несколько
способов выражения концентрации
растворов.
Молярная
концентрация, или молярность (СM)
–
количество вещества (ν) растворенного
компонента, содержащееся в 1 литре (дм3)
раствора:
[моль/л], (14)
Молярная
концентрация эквивалентов
(Сэкв),
(нормальная
концентрация или нормальность
N)
– количество вещества эквивалентов
(νэкв)
растворенного компонента, содержащееся
в 1 литре (дм3)
раствора:
Сэкв
(N)
= νэкв
/ V
[моль-экв/л] (15)
Моляльная
концентрация
или
моляльность
(b)
– количество вещества (ν) растворенного
компонента в 1 кг раствора:
[моль/кг], (16)
Массовая
доля
(ω)
–
отношение массы растворенного вещества
(mр.в.)
к массе раствора (mр-ра)
Ее рассчитывают, выражая в долях единицы
или в процентах. Массовая доля, выраженная
в процентах, называется процентной
концентрацией:
(17)
Процентная
концентрация показывает массу
растворенного вещества, содержащегося
в 100 г раствора. Например, ω(KOH)
= 3% означает, что в 100 г этого раствора
содержится 3 г KOH
и
97 г
H2O.
Молярная
доля (Ni)
– отношение количества вещества
растворенного компонента (в-ва)
(или растворителя, р-ля)
к суммарному количеству вещества всех
компонентов раствора. Например, в
системе, состоящей из растворителя и
одного растворенного вещества, молярная
доля растворенного вещества равна:
, (18)
Молярная доля
растворителя:
(19)
Примеры решения задач
Пример 1.
Определить молярную концентрацию
раствора NaOH
с массовой долей 10% и плотностью
=1,1 г/см3.
Р е ш е н и е. 1) Записываем выражение для молярной концентрации раствора NaOh :
2)
10%-ный раствор – это 10г NaOH
в 100г раствора. Находим количество
вещества NaOH,
содержащееся в 10 г:
,
mNaOH
= 10 г, MNaOH
= 23 + 16 +1 = 40 г/моль
,
т.е. 0,25 моль NaOH
содержится в 100 г раствора.
3)
Находим объем раствора массой 100 г:
m=V,
=
0,091 л
4)
Рассчитываем молярную концентрацию:
Ответ:
молярная концентрация раствора гидроксида
натрия с массовой долей 10% составляет
2,74 моль/л
Пример
2. Найти
молярную долю растворенного вещества
в растворе сахарозы с массовой долей
67%.
Р е ш е н и е. 1) Вспомним, что молярная доля растворенного вещества равна:
67%-ный (по массе)
раствор означает, что в 100 г раствора
содержится 67 г сахарозы и 33 г воды.
2) Определяем
количество вещества сахарозы и количество
вещества воды:
в-ва
= 67/342 = 0,196 моль,
р-ля
= 33/18 = 1,83 моль
Следовательно,
молярная доля сахарозы равна:
Ответ: молярная
доля сахарозы в растворе сахарозы с
массовой долей 67% составляет 0,097.
Пример
3.
Какой объем серной кислоты с массовой
долей 96% (плотностью 1,84 г/см3)
и какую массу воды нужно взять для
приготовления 100 мл 15%-ного (по массе)
раствора H2SO4
(
= 1,10 г/см3).
Р е ш е н и е. 1) Найдем массу 100 мл 15% раствора h2so4:
mH2SO4-р-ра
= V
= 1001,10
=110 г.
2)
Из формулы массовой доли находим массу
серной кислоты, содержащейся в этом
растворе:
;
mH2SO4
=
3)
Найдем массу 96% раствора, содержащего
16,5 г H2SO4:
4)
Находим объем 96 %-ного раствора серной
кислоты:
Ответ:
для приготовления 100мл 15%-ного раствора
H2SO4
потребуется 9,3 мл 96%-ного раствора серной
кислоты и 110 – 16,5 = 93,5 г воды.
Соседние файлы в папке ЗКТэССО
- #
- #
- #
- #
- #
- #
- #
- #
- #
Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.
Растворы. Способы выражения концентрации растворов
Способы выражения концентрации растворов
Существуют различные способы выражения концентрации растворов.
Массовая доля ω компонента раствора определяется как отношение массы данного компонента Х, содержащегося в данной массе раствора к массе всего раствора m. Массовая доля – безразмерная величина, её выражают в долях от единицы:
ωр.в. = mр.в./mр-ра (0 < ωр.в. < 1) (1)
Массовый процент представляет собой массовую долю, умноженную на 100:
ω(Х) = m(Х)/m · 100% (0% < ω(Х) < 100%) (2)
где ω(X) – массовая доля компонента раствора X; m(X) – масса компонента раствора X; m – общая масса раствора.
Мольная доля χ компонента раствора равна отношению количества вещества данного компонента X к суммарному количеству вещества всех компонентов в растворе.
Для бинарного раствора, состоящего из растворённого вещества Х и растворителя (например, Н2О), мольная доля растворённого вещества равна:
χ(X) = n(X)/(n(X) + n(H2O)) (3)
Мольный процент представляет мольную долю, умноженную на 100:
χ(X), % = (χ(X)·100)% (4)
Объёмная доля φ компонента раствора определяется как отношение объёма данного компонента Х к общему объёму раствора V. Объёмная доля – безразмерная величина, её выражают в долях от единицы:
φ(Х) = V(Х)/V (0 < φ(Х) < 1) (5)
Объёмный процент представляет собой объёмную долю, умноженную на 100.
φ(X), % = (φ(X)·100)%
Молярность (молярная концентрация) C или Cм определяется как отношение количества растворённого вещества X, моль к объёму раствора V, л:
Cм(Х) = n(Х)/V (6)
Основной единицей молярности является моль/л или М. Пример записи молярной концентрации: Cм(H2SO4) = 0,8 моль/л или 0,8М.
Нормальность Сн определяется как отношение количества эквивалентов растворённого вещества X к объёму раствора V:
Cн(Х) = nэкв.(Х)/V (7)
Основной единицей нормальности является моль-экв/л. Пример записи нормальной концентрации: Сн(H2SO4) = 0,8 моль-экв/л или 0,8н.
Титр Т показывает, сколько граммов растворённого вещества X содержится в 1 мл или в 1 см3 раствора:
T(Х) = m(Х)/V (8)
где m(X) – масса растворённого вещества X, V – объём раствора в мл.
Моляльность раствора μ показывает количество растворённого вещества X в 1 кг растворителя:
μ(Х) = n(Х)/mр-ля (9)
где n(X) – число моль растворённого вещества X, mр-ля – масса растворителя в кг.
Мольное (массовое и объёмное) отношение – это отношение количеств (масс и объёмов соответственно) компонентов в растворе.
Необходимо иметь ввиду, что нормальность Сн всегда больше или равна молярности См. Связь между ними описывается выражением:
См = Сн · f(Х) (10)
Для получения навыков пересчёта молярности в нормальность и наоборот рассмотрим табл. 1. В этой таблице приведены значения молярности См, которые необходимо пересчитать в нормальность Сн и величины нормальности Сн, которые следует пересчитать в молярность См.
Пересчёт осуществляем по уравнению (10). При этом нормальность раствора находим по уравнению:
Сн = См/f(Х) (11)
Результаты расчётов приведены в табл. 2.
Таблица 1. К определению молярности и нормальности растворов
| Тип химического превращения | См | Сн | Сн | См |
| Реакции обмена | 0,2 M Na2SO4 | ? | 6 н FeCl3 | ? |
| 1,5 M Fe2(SO4)3 | ? | 0,1 н Ва(ОН)2 | ? | |
| Реакции окисления-восстановления | 0,05 М KMnO4
в кислой среде |
? | 0,03 М KMnO4
в нейтральной среде |
? |
Таблица 2
Значения молярности и нормальности растворов
| Тип химического превращения | См | Сн | Сн | См |
| Реакции обмена | 0,2M Ma2SO4 | 0,4н | 6н FeCl3 | 2М |
| 1,5M Fe2(SO4)3 | 9н | 0,1н Ва(ОН)2 | 0,05М | |
| Реакции окисления-восстановления | 0,05М KMnO4 в кислой среде | 0,25н | 0,03М KMnO4
в нейтральной среде |
0,01М |
Между объёмами V и нормальностями Сн реагирующих веществ существует соотношение:
V1 Сн,1 =V2 Сн,2 (12)
Примеры решения задач
Задача 1. Рассчитайте молярность, нормальность, моляльность, титр, мольную долю и мольное отношение для 40 мас.% раствора серной кислоты, если плотность этого раствора равна 1,303 г/см3.
Решение.
Масса 1 литра раствора равна М = 1000·1,303 = 1303,0 г.
Масса серной кислоты в этом растворе: m = 1303·0,4 = 521,2 г.
Молярность раствора См = 521,2/98 = 5,32 М.
Нормальность раствора Сн = 5,32/(1/2) = 10,64 н.
Титр раствора Т = 521,2/1000 = 0,5212 г/см3.
Моляльность μ = 5,32/(1,303 – 0,5212) = 6,8 моль/кг воды.
Обратите внимание на то, что в концентрированных растворах моляльность (μ) всегда больше молярности (См). В разбавленных растворах наоборот.
Масса воды в растворе: m = 1303,0 – 521,2 = 781,8 г.
Количество вещества воды: n = 781,8/18 = 43,43 моль.
Мольная доля серной кислоты: χ = 5,32/(5,32+43,43) = 0,109. Мольная доля воды равна 1– 0,109 = 0,891.
Мольное отношение равно 5,32/43,43 = 0,1225.
Задача 2. Определите объём 70 мас.% раствора серной кислоты (r = 1,611 г/см3), который потребуется для приготовления 2 л 0,1 н раствора этой кислоты.
Решение.
2 л 0,1н раствора серной кислоты содержат 0,2 моль-экв, т.е. 0,1 моль или 9,8 г.
Масса 70%-го раствора кислоты m = 9,8/0,7 = 14 г.
Объём раствора кислоты V = 14/1,611 = 8,69 мл.
Задача 3. В 5 л воды растворили 100 л аммиака (н.у.). Рассчитать массовую долю и молярную концентрацию NH3 в полученном растворе, если его плотность равна 0,992 г/см3.
Решение.
Масса 100 л аммиака (н.у.) m = 17·100/22,4 = 75,9 г.
Масса раствора m = 5000 + 75,9 = 5075,9 г.
Массовая доля NH3 равна 75,9/5075,9 = 0,0149 или 1,49 %.
Количество вещества NH3 равно 100/22,4 = 4,46 моль.
Объём раствора V = 5,0759/0,992 = 5,12 л.
Молярность раствора См = 4,46/5,1168 = 0,872 моль/л.
Задача 4. Сколько мл 0,1М раствора ортофосфорной кислоты потребуется для нейтрализации 10 мл 0,3М раствора гидроксида бария?
Решение.
Переводим молярность в нормальность:
0,1 М Н3РО4 0,3 н; 0,3 М Ва(ОН)2 0,6 н.
Используя выражение (12), получаем: V(H3P04)=10·0,6/0,3 = 20 мл.
Задача 5. Какой объем, мл 2 и 14 мас.% растворов NaCl потребуется для приготовления 150 мл 6,2 мас.% раствора хлорида натрия?
Плотности растворов NaCl:
| С, мас.% | 2 | 6 | 7 | 14 |
| ρ, г/см3 | 2,012 | 1,041 | 1,049 | 1,101 |
Решение.
Методом интерполяции рассчитываем плотность 6,2 мас.% раствора NaCl:
6,2% =6% + 0,2(7% —6% )/(7 – 6) = 1,0410 + 0,0016 = 1,0426 г/см3.
Определяем массу раствора: m = 150·1,0426 = 156,39 г.
Находим массу NaCl в этом растворе: m = 156,39·0,062 = 9,70 г.
Для расчёта объёмов 2 мас.% раствора (V1) и 14 мас.% раствора (V2) составляем два уравнения с двумя неизвестными (баланс по массе раствора и по массе хлорида натрия):
156,39 = V1 1,012 + V2 1,101 ,
9,70 = V1·1,012·0,02 + V2·1,101·0,14 .
Решение системы этих двух уравнений дает V1 =100,45 мл и V2 = 49,71 мл.
Задачи для самостоятельного решения
3.1. Рассчитайте нормальность 2 М раствора сульфата железа (III), взаимодействующего со щёлочью в водном растворе.
12 н.
3.2. Определите молярность 0,2 н раствора сульфата магния, взаимодействующего с ортофосфатом натрия в водном растворе.
0,1 M.
3.3. Рассчитайте нормальность 0,02 М раствора KMnO4, взаимодействующего с восстановителем в нейтральной среде.
0,06 н.
3.4. Определите молярность 0,1 н раствора KMnO4, взаимодействующего с восстановителем в кислой среде.
0,02 M.
3.5. Рассчитать нормальность 0,2 М раствора K2Cr2O7, взаимодействующего с восстановителем в кислой среде.
1,2 M.
3.6. 15 г CuSO4·5H2O растворили в 200 г 6 мас.% раствора CuSO4. Чему равна массовая доля сульфата меди, а также молярность, моляльность и титр полученного раствора, если его плотность составляет 1,107 г/мл?
0,1; 0,695М; 0,698 моль/кг; 0,111 г/мл.
3.7. При выпаривании 400 мл 12 мас.% раствора KNO3 (плотность раствора 1,076 г/мл) получили 2М раствор нитрата калия. Определить объём полученного раствора, его нормальную концентрацию и титр.
255 мл; 2 н; 0,203 г/мл.
3.8. В 3 л воды растворили 67,2 л хлороводорода, измеренного при нормальных условиях. Плотность полученного раствора равна 1,016 г/мл. Вычислить массовую, мольную долю растворённого вещества и мольное отношение растворённого вещества и воды в приготовленном растворе.
0,035; 0,0177; 1:55,6.
3.9. Сколько граммов NaCl надо добавить к 250 г 6 мас.% раствору NaCl, чтобы приготовить 500 мл раствора хлорида натрия, содержащего 16 мас.% NaCl? Плотность полученного раствора составляет 1,116 г/мл. Определить молярную концентрацию и титр полученного раствора.
74,28 г; 3,05 М; 0,179 г/мл.
3.10. Определить массу воды, в которой следует растворить 26 г ВaCl2·2H2O для получения 0,55М раствора ВaCl2 (плотность раствора 1,092 г/мл). Вычислить титр и моляльность полученного раствора.
192,4 г; 0,111 г/мл; 0,56 моль/кг.
В ПОМОЩЬ МОЛОДОМУ
УЧИТЕЛЮ
Расчеты концентрации
растворенных веществ
в растворах
Решение задач на разбавление растворов особой
сложности не представляет, однако требует
внимательности и некоторого напряжения. Тем не
менее можно упростить решение этих задач,
используя закон разбавления, которым пользуются
в аналитической химии при титровании растворов.
Во всех задачниках по химии показаны решения
задач, представленных как образец решения, и во
всех решениях используется закон разбавления,
принцип которого состоит в том, что количество
растворенного вещества и масса m в исходном и разбавленном
растворах остаются неизменными. Когда мы решаем
задачу, то это условие держим в уме, а расчет
записываем по частям и постепенно, шаг за шагом,
приближаемся к конечному результату.
Рассмотрим проблему решения задач на
разбавление, исходя из следующих соображений.
• Количество растворенного вещества :
= c•V,
где c – молярная концентрация
растворенного вещества в моль/л, V – объем
раствора в л.
• Масса растворенного вещества m(р.в.):
m(р. в.) = m(р-ра)•,
где m(р-ра) – масса раствора в г, – массовая доля
растворенного вещества.
Обозначим в исходном (или неразбавленном)
растворе величины c, V, m(р-ра), через с1, V1,
m1(р-ра), 1,
а в разбавленном растворе – через с2, V2,
m2(р-ра), 2.
Составим уравнения разбавления растворов. Левые
части уравнений отведем для исходных
(неразбавленных) растворов, а правые части – для
разбавленных растворов.
Неизменность количества растворенного вещества
при разбавлении будет иметь вид:
Сохранение массы m(р. в.):
Количество растворенного вещества связано с его массой m
(р. в.) cоотношением:
= m(р.
в.)/M(р. в.),
где M(р. в.) – молярная масса растворенного
вещества в г/моль.
Уравнения разбавления (1) и (2) связаны между собой
следующим образом:
с1•V1 = m2(р-ра)•2/M(р. в.),
m1(р-ра)•1 = с2•V2•M(р.
в.).
Если в задаче известен объем растворенного
газа V(газа), то его количество вещества связано с объемом
газа (н.у.) отношением:
= V(газа)/22,4.
Уравнения разбавления примут соответственно
вид:
V(газа)/22,4 = с2•V2,
V(газа)/22,4 = m2(р-ра)•2/M(газа).
Если в задаче известны масса вещества или
количество вещества, взятого для приготовления
раствора, то в левой части уравнения разбавления
ставится m(р. в.) или , в зависимости от условия задачи.
Если по условию задачи требуется объединить
растворы разной концентрации одного и того же
вещества, то в левой части уравнения массы
растворенных веществ суммируются.
Довольно часто в задачах используется плотность
раствора (г/мл). Но
поскольку молярная концентрация с
измеряется в моль/л, то и плотность следует
выражать в г/л, а объем V – в л.
Приведем примеры решения «образцовых» задач.
Задача 1. Какой
объем 1М раствора серной кислоты надо взять,
чтобы получить 0,5 л 0,1М H2SO4?
Дано:
с1 = 1 моль/л,
V2 = 0,5 л,
с2 = 0,1 моль/л.
Найти:
V1 = ?
Решение
V1•с1 = V2•с2,
V1•1 = 0,5•0,1; V1 = 0,05 л,
или 50 мл.
Ответ. V1 = 50 мл.
Задача 2 ([1],
№ 4.23). Определите массу раствора с массовой
долей (СuSО4)
10% и массу воды, которые потребуются для
приготовления раствора массой 500 г с массовой
долей
(СuSО4) 2%.
Дано:
1 = 0,1,
m2(р-ра) = 500 г,
2 = 0,02.
Найти:
m1(р-ра) = ?
m(H2O) = ?
Решение
m1(р-ра)•1 = m2(р-ра)•
2,
m1(р-ра)•0,1 = 500•0,02.
Отсюда m1(р-ра) = 100 г.
Найдем массу добавляемой воды:
m(H2O) = m2(р-ра) – m1(р-ра),
m(H2O) = 500 – 100 = 400 г.
Ответ. m1(р-ра) = 100 г, m(H2O)
= 400 г.
Задача 3 ([1],
№ 4.37). Какой объем раствора с массовой долей
серной кислоты 9,3%
( = 1,05 г/мл)
потребуется для приготовления 0,35М раствора H2SO4
объемом 40 мл?
Дано:
1 = 0,093,
1 = 1050 г/л,
с2 = 0,35 моль/л,
V2 = 0,04 л,
М(H2SO4) = 98 г/моль.
Найти:
V1 = ?
Решение
m1(р-ра)•1 = V2•с2•М(H2SO4),
V1•1•
1
= V2• с2•М(H2SO4).
Подставляем значения известных величин:
V1•1050•0,093 = 0,04•0,35•98.
Отсюда V1 = 0,01405 л, или 14,05 мл.
Ответ. V1 = 14,05 мл.
Задача 4 [2]. Какой
объем хлороводорода (н.у.) и воды потребуется,
чтобы приготовить 1 л раствора ( = 1,05 г/см3), в котором
содержание хлороводорода в массовых долях равно
0,1
(или 10%)?
Дано:
V(р-ра) = 1 л,
(р-ра) = 1050 г/л,
= 0,1,
М(HCl) = 36,5 г/моль.
Найти:
V(HCl) = ?
m(H2O) = ?
Решение
V(HCl)/22,4 = m(р-ра)•/М(HCl),
V(HCl)/22,4 = V(р-ра)•(р-ра)•
/М(HCl),
V(HCl)/22,4 = 1•1050•0,1/36,5.
Отсюда V(HCl) = 64,44 л.
Найдем массу добавляемой воды:
m(H2O) = m(р-ра) – m(HСl),
m(H2O) = V(р-ра)•(р-ра) – V(HCl)/22,4• М(HCl),
m(H2O) = 1•1050 – 64,44/22,4•36,5 = 945 г.
Ответ. 64,44 л HCl и 945 г воды.
Задача 5 ([1],
№ 4.34). Определите молярную концентрацию
раствора с массовой долей гидроксида натрия 0,2 и
плотностью 1,22 г/мл.
Дано:
= 0,2,
= 1220 г/л,
М(NaOH) = 40 г/моль.
Найти:
c = ?
Решение
m(р-ра)• = с•V•М(NaOH),
m(р-ра)• = с•m(р-ра)•М(NaOH)/
.
Разделим обе части уравнения на m(р-ра) и
подставим численные значения величин.
0,2 = c•40/1220.
Отсюда c = 6,1 моль/л.
Ответ. c = 6,1 моль/л.
Задача 6 ([1],
№ 4.30). Определите молярную концентрацию
раствора, полученного при растворении сульфата
натрия массой 42,6 г в воде массой 300 г, если
плотность полученного раствора равна 1,12 г/мл.
Дано:
m(Na2SO4) = 42,6 г,
m(H2O) = 300 г,
= 1120 г/л,
M(Na2SO4) = 142 г/моль.
Найти:
c = ?
Решение
m(Na2SO4) = с•V•М(Na2SO4).
Подставляя численные значения, получим:
42,6 = с•(42,6 + 300)/1120•142.
Отсюда с = 0,98 моль/л.
Ответ. с = 0,98 моль/л.
Задача 7 ([1],
№ 4.19). В лаборатории имеются растворы с
массовой долей хлорида натрия 10% и 20%. Какую массу
каждого раствора надо взять для получения
раствора с массовой долей соли 12% и массой 300 г?
Дано:
1 = 0,1,
2 = 0,2,
3 = 0,12,
m3(р-ра) = 300 г.
Найти:
m1(р-ра) = ?
m2(р-ра) = ?
Решение
m1(р-ра)•1 + m2(р-ра)•
2 = m3(р-ра)•
3,
m1(р-ра)•0,1 + m2(р-ра)•0,2
= 300•0,12.
Поскольку m1(р-ра) + m2(р-ра) = 300
г, то получаем систему из двух уравнений с двумя
неизвестными. Решая совместно два уравнения,
находим:
m1(р-ра) = 240 г, m2(р-ра) =
60 г.
Ответ. m1(р-ра) = 240 г, m2(р-ра)
= 60 г.
Задача 8 ([1],
№ 4.48). В воде массой 100 г при температуре 0 °С
растворяется фторид натрия массой 4,1 г, а при
температуре 40 °С – массой 4,5 г. Какая масса
фторида натрия выпадет в осадок при охлаждении
насыщенного при температуре 40 °С раствора NaF
массой 500 г до температуры 0 °С?
Дано:
m1(NaF) = 4,1 г,
m2(NaF) = 4,5 г,
m2(р-ра) = 500 г,
– массовая доля
NaF,
(1 – ) – массовая
доля воды.
Найти:
m(NaF) = ?
Решение
m(NaF) = m2(р-ра) – m1(р-ра).
Поскольку m2(Н2О) (40 °С) = m1(Н2О)
(0 °С), то можно записать:
m2(р-ра)•(1 – 2) = m1(р-ра)•(1 –
1).
Подставляем значения:
500•(1 – 4,5/(4,5 + 100)) = m1(р-ра)•(1 –
4,1/(4,1 + 100)).
Отсюда m1(р-ра) = 104,1/104,5•500 = 498,09 г,
m(NaF) = 500 – 498,09 = 1,91 г.
Ответ. m(NaF) = 1,91 г.
ЛИТЕРАТУРА
1. Хомченко Г.П., Хомченко И.Г. Задачи по химии
для поступающих в вузы. М.: Новая волна, 2002.
2. Фельдман Ф.Г., Рудзитис Г.Е. Химия-9. М.:
Просвещение, 1990, с. 166.
В.И.МАРТЫНОВ,
учитель химии
(пос. Архипо-Осиповка, Краснодарский край)
Основные понятия и определения
Под раствором в химии понимают твёрдую или жидкую однородную систему, состоящую из нескольких компонентов. Вещества образующие раствор разделяются на растворители и растворённые.
Например, сахар, находящийся в воде — такая смесь называется двухгомогенная. Если же в сахарную воду добавить уксус, то полученный раствор уже будет трёхгомогенный. Количество в смеси того или иного разжиженного компонента называется концентрацией. Изменяться она может в широких пределах.
Существует несколько способов выражения концентрации растворов:
- Массовый. Обозначается латинской буквой P и определяется количеством растворённого вещества в 100 граммах смеси. Для нахождения массовой концентрации используется формула: P = (n / (n + m)) * 100%, где: n — масса растворяемого вещества, m — масса растворителя, (n + m) — масса раствора. Сумма веществ выражается произведением объёма раствора на его плотность, то есть (n + m) = p * V и измеряется в граммах. Например, 25% раствор обозначает, что в 100 граммах смеси содержится 25 грамм вещества n.
- Молярный. Показывает количество моль разжиженного тела в одном кубическом дециметре. Обозначается характеристика латинскими символами Cb и находится из выражения: Cb = v моль / V дм³. То есть запись: 0,6 M NaCl будет означать, что 0,6 моль NaCl растворено в одном кубическом дециметре смеси.
- Эквивалентный. Способ ещё называется нормальным. Он так же как и молярный показывает количество растворённого вещества в дециметре кубическом, только используется моль эквивалента. Под последним понимается количество соединений с одним молем атома или замещения при прохождении реакций. Обозначается символом Cэ и находится по формуле Cэ = n / Mэкв * V дм³. Например, 0,1 HCl означает, что 0,1 моль эквивалента соляной кислоты содержится в 1 дм³ раствора.
- Моляльный. Используется, чтобы узнать, какое количество моль разжиженного вещества находится в килограмме растворителя. Моляльность рассчитывается с помощью формулы: Cm = (n*100) / (M * m).
- Титр раствора. Определяется количеством растворённого вещества, выраженного в одном сантиметре кубическом. Измеряется в граммах: Т = n / V см³.
Молярная масса и доли
Для измерения массы используются граммы, килограммы, тонны, но для обозначения количества вещества они не подходят. В химических процессах принимают участие различные частицы, такие как молекулы, атомы, ионы. Поэтому для того чтобы определить, сколько вещества содержится в той или иной смеси, ввели специальную единицу — моль. Иными словами — это множество, в котором объединены масса с числом.
Концентрация — это значение количества объёма раствора к растворенному в нём телу. Наиболее часто для измерения применяется массовая доля разжиженного вещества, молярная и нормальная концентрация. Массовая часть — это неизмеряемая величина. Складывается она из двух масс:
- растворителя — вещества способного ослаблять другие тела;
- растворимого — разжижающегося состава, поглощаемого растворителем.
Способность же вещества поглощаться другим называют растворимостью. При определении результата взаимодействия растворов находится массовая доля каждого из них.
Молярная масса показывает массу одного моль вещества и измеряется в граммах, делённых на моль. Если необходимо отмерить один моль, то нужно будет взять столько граммов вещества, сколько их содержится в относительной атомной массе или же, относительной молекулярной массе. Один моль всегда содержит постоянное число молекул, называемое константой Авогадро. Равно оно: N = 6 * 1023. Для того чтобы рассчитать число молекул в определённом веществе используют формулу:
N = Na * n, где Na — постоянная Авогадро, n — количество вещества. То есть моль — это количество в котором содержится 6 * 1023 молекул. Молярная концентрация определяет, сколько моль разжиженного вещества содержится в одном литре раствора.
Считается, что в единице объёма находится некая величина, определяемая числом молекул. Записывается это определение как n = N / V и называется концентрацией молекул. Измеряется она в м3. Важно отметить, что концентрация связана с плотностью соотношением: n = p / m0 и показывает число структурных молекул, находящихся в единице объёме. Поэтому плотность используется при нахождении массы на единицу объёма, а концентрация при вычислении количества молекул.
Массовая доля растворимого часто называется процентной концентрацией. При этом вместо процентного определения используется молярная концентрация. Другими словами, отношение количества к объёму в литрах. Зная число молей в одном литре довольно просто подобрать необходимое число молей используя специальную посуду.
Формулы перехода
Расчёт количества той или иной части концентрированной смеси, возможно, выполнить в различных единицах. Но между тем существуют формулы перехода от одних выражений к другим. При пересчёте происходит округление знака после запятой, поэтому при переходе с одной величины на другую появляется определённая погрешность.
Конвертация от массовой доли к молярной массе выполняется по формуле: Cb = (p * ɷb) / M (B), где: Cb — молярная концентрация, p — плотность, ɷb — массовая доля, M (B) — молярная масса. При этом когда плотность раствора изначально обозначается в грамм на миллилитр, а молярная в грамм на моль, то ответ необходимо умножить на 1 тыс. мл/л. Если же значение доли указано в процентах, то ответ необходимо разделить на 100%.
Для перехода от молярной к нормальной концентрации (молярной концентрации эквивалента), используется выражение: c * ((1 / z) * B) = Cb * z. Где молярность измеряется в моль на литр, а z — число эквивалентности (сопоставимое с одним молем катионов водорода в проходящей реакции). В определённых ситуациях выполняется и перевод массовой доли к титру. Выполняют это по формуле: T = p * ɷ, где p — плотность, измеряемая в граммах, делённых на миллилитры, а ɷ — массовая часть растворённого, в долях.
Перевести можно и молярность к титру. Используют для этого следующую формулу перехода: Т = Cb * M, в которой М — молярная масса разжиженного вещества. В случае же когда концентрация выражается в моль на литр, а масса в грамм на моль, ответ нужно разделить на 1 тыс. миллилитров на литр. Молярность связана с моляльностью формулой: mb = Cb / p, где р — плотность раствора, измеряемая в граммах, делённых на миллилитры.
Самый же сложный перевод происходит при конвертации моляльности к мольной доле. Для решения такой задачи используется формула для мольного элемента: Yb = mb / (mb + 1/ M (A)). В выражении mb обозначает моляльность, а M (A) — молярную массу растворителя. Чтобы ответ получился в одинаковых единицах измерения, цифра один в формуле представляется как 1000 г/кг. Это необходимо, когда моляльность подставляется в моль на килограмм, а масса в грамм на моль.
Вычисление концентрации
Чтобы получить раствор, необходимо между собой смешать растворитель и растворимое. Для того чтобы вычислить концентрацию, нужно знать или найти общий объём смеси, который будет равен сумме элементов, используемых при создании раствора. Измеряться концентрация может в различных величинах. Основные из них:
- грамм на литр (г/л) — отношение массы к объёму;
- молярность (моль) — содержание растворенных элементов к объёму раствора;
- миллионная часть (г / единица раствора) — соотношение растворённых веществ к одному миллиону единиц смеси;
- проценты (%) — ответ выражается в количестве растворённой доли в граммах к ста частям раствора.
Найти молярность, характеризуемую числом доли растворенных элементов, зная массу и формулу вещества несложно. Если количество растворённой части задано в других единицах, то их преобразуют в граммы.
Каждый элемент характеризуется молярной массой и определяется отношением массы к числу моль. Равна она атомной массе, которую можно взять из таблицы Менделеева. Для нахождения молярной величины нужно сложить все атомные числа элементов, смешанных в растворе.
Найдя молекулярное значение можно перейти к вычислению количества молей. Делается это с помощью формулы для молярной концентрации: масса растворённого вещества умножается на обратную молярную часть. Результат должен получиться в моль. На следующем этапе находится молярность. Полученное число молей делится на объём, измеряемого в литрах раствора. Обычно объёмом растворённой части пренебрегают.
По аналогии вычисляется концентрация и в процентном составе. Для этого нужно найти массу частей, составляющих раствор. На первом этапе все единицы измерения переводятся в граммы. Находится плотность, затем она умножается на объём и получается масса вещества в граммах. Вычисление концентрации в процентном составе находится как масса растворённого вещества, делённая на сумму массы растворяемого и растворителя, а после результат умножается на сто.
Так как проценты являются сотой долей, то для получения ответа в миллионной доле результат нужно умножить ещё на 10 тысяч.
Примеры расчёта
Определением молярности раствора занимается химия. В процессах участвуют различные частицы, количество которых даже в малых объёмах велико. Значение молярной концентрации определяется не только количественным, но и качественным составом. Самые простые задачи связаны с нахождением молярной массы. Например, для соединения CH4 она наводится следующим образом:
Мr (CH4) = Ar + 4Ar (H) = 12 + 4 =16
Получается, что масса метана содержит 16 г/моль или 6,02Ч * 1023 молекул. Буква «Ч» используется для обозначения части.
Теперь можно найти массу в объёмном количестве. Например, нужно определить массу метана смешанном в количестве двух моль. Так как для метана его масса составляет 16 г/моль, то ответом будет:
м (метан) = 2 * 16 = 32 г
Много задач встречается на нахождение массовой доли в растворе. Например, в 200 грамм соли добавили 80 грамм воды. Чтобы определить часть соли в полученной смеси необходимо найти первоначальную её долю в растворе: M1 = w * m = 0,14 * 200 = 28 гамм. Затем вычислить массу нового раствора: М2 = 200 + 80 = 280 грамм. И воспользовавшись формулой получить ответ: W = M1 / M2 = 28 / 280 = 0,100.
Немного сложнее задачи на расчёт грамм-эквивалента. Пусть нужно найти нормальность серной кислоты, смешанной с раствором щёлочи. При смешении образуется соединение: NaSO4. Так как при реакции серная кислота нейтрализует гидросульфат натрия только частично то можно записать: Н2SO4 + NaOH = NaHSO4 + Н2О. Серная кислота представляет основу равную единице, поэтому и фактор эквивалентности также будет составлять единицу.
Экв (H2SO4) =1 * ф = 1/1 = 1
Отсюда следует, что значение молярности эквивалента кислоты:
Мэкв (H2SO4) = M * Ф = M/1 = 98/1 = 98 г/экв
Нужно найти массовую часть и молярность эквивалента смеси, полученной при смешивании 400 мл раствора серной кислоты (p =1, 18 г/мл) и 400 мл восьмипроцентного раствора серной кислоты (p = 1,05 г/мл).
Вначале следует вычислить массу первого раствора и содержание в нём серной кислоты:
m (р-ра) = p (р-ра) * V (р-ра) = 1,18 * 400 = 720 г
m (H2SO4) = V (H2SO4) * м (H2SO4)= С (H2SO4) * V (р-ра) * М (H2SO4) = 720 * 0,2 — 98 = 46 г
Затем определить массу второго раствора и содержание в нём количества серной кислоты:
m (р-ра) = р (р-ра) * V (р-ра) = 1,05 * 400 = 420 г
m = m (р-ра) * (H2SO4)= 420 * 0,08 = 24 г
Часть полученного раствора находится по формуле:
ɷ (H2SO4) = m (H2SO4) / m (р-ра) = (46 + 24) / (720+420) = 0,146
Ответ удобнее записать в процентном соотношении — 14,6%.
From Wikipedia, the free encyclopedia
«Molarity» redirects here. Not to be confused with Molality or Morality.
| Molar concentration | |
|---|---|
|
Common symbols |
c |
| SI unit | mol/m3 |
|
Other units |
mol/L |
|
Derivations from |
c = n/V |
| Dimension |  |
Molar concentration (also called molarity, amount concentration or substance concentration) is a measure of the concentration of a chemical species, in particular of a solute in a solution, in terms of amount of substance per unit volume of solution. In chemistry, the most commonly used unit for molarity is the number of moles per liter, having the unit symbol mol/L or mol/dm3 in SI unit. A solution with a concentration of 1 mol/L is said to be 1 molar, commonly designated as 1 M.
Definition[edit]
Molar concentration or molarity is most commonly expressed in units of moles of solute per litre of solution.[1] For use in broader applications, it is defined as amount of substance of solute per unit volume of solution, or per unit volume available to the species, represented by lowercase 
Here, 





In thermodynamics the use of molar concentration is often not convenient because the volume of most solutions slightly depends on temperature due to thermal expansion. This problem is usually resolved by introducing temperature correction factors, or by using a temperature-independent measure of concentration such as molality.[3]
The reciprocal quantity represents the dilution (volume) which can appear in Ostwald’s law of dilution.
- Formality or analytical concentration
If a molecular entity dissociates in solution, the concentration refers to the original chemical formula in solution, the molar concentration is sometimes called formal concentration or formality (FA) or analytical concentration (cA). For example, if a sodium carbonate solution (Na2CO3) has a formal concentration of c(Na2CO3) = 1 mol/L, the molar concentrations are c(Na+) = 2 mol/L and c(CO2−3) = 1 mol/L because the salt dissociates into these ions.[4]
Units[edit]
In the International System of Units (SI) the coherent unit for molar concentration is mol/m3. However, this is inconvenient for most laboratory purposes and most chemical literature traditionally uses mol/dm3, which is the same as mol/L. This traditional unit is often called a molar and denoted by the letter M, for example:
- mol/m3 = 10−3 mol/dm3 = 10−3 mol/L = 10−3 M = 1 mM = 1 mmol/L.
To avoid confusion with SI prefix mega, which has the same abbreviation, small caps ᴍ or italicized M are also used in journals and textbooks.[5]
Sub-multiples such as millimolar consist of the unit preceded by an SI prefix:
| Name | Abbreviation | Concentration | |
|---|---|---|---|
| (mol/L) | (mol/m3) | ||
| millimolar | mM | 10−3 | 100=1 |
| micromolar | μM | 10−6 | 10−3 |
| nanomolar | nM | 10−9 | 10−6 |
| picomolar | pM | 10−12 | 10−9 |
| femtomolar | fM | 10−15 | 10−12 |
| attomolar | aM | 10−18 | 10−15 |
| zeptomolar | zM | 10−21 | 10−18 |
| yoctomolar | yM | 10−24 (6 particles per 10 L) |
10−21 |
| rontomolar | rM | 10−27 | 10−24 |
| quectomolar | qM | 10−30 | 10−27 |
[edit]
Number concentration[edit]
The conversion to number concentration 
where 
Mass concentration[edit]
The conversion to mass concentration 
where 

Mole fraction[edit]
The conversion to mole fraction 
where 

A simpler relation can be obtained by considering the total molar concentration, namely, the sum of molar concentrations of all the components of the mixture:
Mass fraction[edit]
The conversion to mass fraction 
Molality[edit]
For binary mixtures, the conversion to molality 
where the solvent is substance 1, and the solute is substance 2.
For solutions with more than one solute, the conversion is
Properties[edit]
Sum of molar concentrations – normalizing relations[edit]
The sum of molar concentrations gives the total molar concentration, namely the density of the mixture divided by the molar mass of the mixture or by another name the reciprocal of the molar volume of the mixture. In an ionic solution, ionic strength is proportional to the sum of the molar concentration of salts.
Sum of products of molar concentrations and partial molar volumes[edit]
The sum of products between these quantities equals one:
Dependence on volume[edit]
The molar concentration depends on the variation of the volume of the solution due mainly to thermal expansion. On small intervals of temperature, the dependence is
where 

Examples[edit]
- 11.6 g of NaCl is dissolved in 100 g of water. The final mass concentration ρ(NaCl) is
- ρ(NaCl) = 11.6 g/11.6 g + 100 g = 0.104 g/g = 10.4 %.
The volume of such a solution is 104.3mL (volume is directly observable); its density is calculated to be 1.07 (111.6g/104.3mL)
The molar concentration of NaCl in the solution is therefore
- c(NaCl) = 11.6 g/58 g/mol / 104.3 mL = 0.00192 mol/mL = 1.92 mol/L.
Here, 58 g/mol is the molar mass of NaCl.
- A typical task in chemistry is the preparation of 100 mL (= 0.1 L) of a 2 mol/L solution of NaCl in water. The mass of salt needed is
- m(NaCl) = 2 mol/L × 0.1 L × 58 g/mol = 11.6 g.
To create the solution, 11.6 g NaCl is placed in a volumetric flask, dissolved in some water, then followed by the addition of more water until the total volume reaches 100 mL.
- The density of water is approximately 1000 g/L and its molar mass is 18.02 g/mol (or 1/18.02 = 0.055 mol/g). Therefore, the molar concentration of water is
- c(H2O) = 1000 g/L/18.02 g/mol ≈ 55.5 mol/L.
Likewise, the concentration of solid hydrogen (molar mass = 2.02 g/mol) is
- c(H2) = 88 g/L/2.02 g/mol = 43.7 mol/L.
The concentration of pure osmium tetroxide (molar mass = 254.23 g/mol) is
- c(OsO4) = 5.1 kg/L/254.23 g/mol = 20.1 mol/L.
- A typical protein in bacteria, such as E. coli, may have about 60 copies, and the volume of a bacterium is about 10−15 L. Thus, the number concentration C is
- C = 60 / (10−15 L) = 6×1016 L−1.
The molar concentration is
- c = C/NA = 6×1016 L−1/6×1023 mol−1 = 10−7 mol/L = 100 nmol/L.
- Reference ranges for blood tests, sorted by molar concentration:
See also[edit]
- Molality
- Orders of magnitude (molar concentration)
References[edit]
- ^ Tro, Nivaldo J. (6 January 2014). Introductory chemistry essentials (Fifth ed.). Boston. p. 457. ISBN 9780321919052. OCLC 857356651.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «amount concentration, c«. doi:10.1351/goldbook.A00295
- ^ a b Kaufman, Myron (2002). Principles of thermodynamics. CRC Press. p. 213. ISBN 0-8247-0692-7.
- ^ Harvey, David (2020-06-15). «2.2: Concentration». Chemistry LibreTexts. Retrieved 2021-12-15.
- ^ «Typography of unit symbols for Molar and Liter in siunitx». TeX — LaTeX Stack Exchange.
External links[edit]
- Molar Solution Concentration Calculator
- Experiment to determine the molar concentration of vinegar by titration