From Wikipedia, the free encyclopedia
| Value of R[1] | Unit |
|---|---|
| SI units | |
| 8.31446261815324 | J⋅K−1⋅mol−1 |
| 8.31446261815324 | m3⋅Pa⋅K−1⋅mol−1 |
| 8.31446261815324 | kg⋅m2⋅s−2⋅K−1⋅mol−1 |
| Other common units | |
| 8314.46261815324 | L⋅Pa⋅K−1⋅mol−1 |
| 8.31446261815324 | L⋅kPa⋅K−1⋅mol−1 |
| 0.0831446261815324 | L⋅bar⋅K−1⋅mol−1 |
| 8.31446261815324×107 | erg⋅K−1⋅mol−1 |
| 0.730240507295273 | atm⋅ft3⋅lbmol−1⋅°R−1 |
| 10.731577089016 | psi⋅ft3⋅lbmol−1⋅°R−1 |
| 1.985875279009 | BTU⋅lbmol−1⋅°R−1 |
| 297.031214 | inH2O⋅ft3⋅lbmol−1⋅°R−1 |
| 554.984319180 | torr⋅ft3⋅lbmol−1⋅°R−1 |
| 0.082057366080960 | L⋅atm⋅K−1⋅mol−1 |
| 62.363598221529 | L⋅Torr⋅K−1⋅mol−1 |
| 1.98720425864083… | cal⋅K−1⋅mol−1 |
| 8.20573660809596…×10−5 | m3⋅atm⋅K−1⋅mol−1 |
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol R or R. It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per particle. The constant is also a combination of the constants from Boyle’s law, Charles’s law, Avogadro’s law, and Gay-Lussac’s law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation.
The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of substance. The Boltzmann constant and the Avogadro constant were similarly determined, which separately relate energy to temperature and particle count to amount of substance.
The gas constant R is defined as the Avogadro constant NA multiplied by the Boltzmann constant k (or kB):
Since the 2019 redefinition of SI base units, both NA and k are defined with exact numerical values when expressed in SI units.[2] As a consequence, the SI value of the molar gas constant is exactly 8.31446261815324 J⋅K−1⋅mol−1.
Some have suggested that it might be appropriate to name the symbol R the Regnault constant in honour of the French chemist Henri Victor Regnault, whose accurate experimental data were used to calculate the early value of the constant. However, the origin of the letter R to represent the constant is elusive. The universal gas constant was apparently introduced independently by Clausius’ student, A.F. Horstmann (1873)[3][4]
and Dmitri Mendeleev who reported it first on Sep. 12, 1874.[5]
Using his extensive measurements of the properties of gases,[6][7]
Mendeleev also calculated it with high precision, within 0.3% of its modern value.[8]
The gas constant occurs in the ideal gas law:
where P is the absolute pressure, V is the volume of gas, n is the amount of substance, m is the mass, and T is the thermodynamic temperature. Rspecific is the mass-specific gas constant. The gas constant is expressed in the same unit as are molar entropy and molar heat.
Dimensions[edit]
From the ideal gas law PV = nRT we get:
where P is pressure, V is volume, n is number of moles of a given substance, and T is temperature.
As pressure is defined as force per area of measurement, the gas equation can also be written as:
Area and volume are (length)2 and (length)3 respectively. Therefore:
Since force × length = work:
The physical significance of R is work per degree per mole. It may be expressed in any set of units representing work or energy (such as joules), units representing degrees of temperature on an absolute scale (such as kelvin or rankine), and any system of units designating a mole or a similar pure number that allows an equation of macroscopic mass and fundamental particle numbers in a system, such as an ideal gas (see Avogadro constant).
Instead of a mole the constant can be expressed by considering the normal cubic meter.
Otherwise, we can also say that:
Therefore, we can write R as:
And so, in terms of SI base units:
- R = 8.314462618… kg⋅m2⋅s−2⋅K−1⋅mol−1.
Relationship with the Boltzmann constant[edit]
The Boltzmann constant kB (alternatively k) may be used in place of the molar gas constant by working in pure particle count, N, rather than amount of substance, n, since
where NA is the Avogadro constant.
For example, the ideal gas law in terms of the Boltzmann constant is
where N is the number of particles (molecules in this case), or to generalize to an inhomogeneous system the local form holds:
where ρN = N/V is the number density.
Measurement and replacement with defined value[edit]
As of 2006, the most precise measurement of R had been obtained by measuring the speed of sound ca(P, T) in argon at the temperature T of the triple point of water at different pressures P, and extrapolating to the zero-pressure limit ca(0, T). The value of R is then obtained from the relation
where:
- γ0 is the heat capacity ratio (5/3 for monatomic gases such as argon);
- T is the temperature, TTPW = 273.16 K by the definition of the kelvin at that time;
- Ar(Ar) is the relative atomic mass of argon and Mu = 10−3 kg⋅mol−1 as defined at the time.
However, following the 2019 redefinition of the SI base units, R now has an exact value defined in terms of other exactly defined physical constants.
Specific gas constant[edit]
| Rspecific for dry air |
Unit |
|---|---|
| 287.052874 | J⋅kg−1⋅K−1 |
| 53.3523 | ft⋅lbf⋅lb−1⋅°R−1 |
| 1,716.46 | ft⋅lbf⋅slug−1⋅°R−1 |
| Based on a mean molar mass for dry air of 28.964917 g/mol. |
The specific gas constant of a gas or a mixture of gases (Rspecific) is given by the molar gas constant divided by the molar mass (M) of the gas or mixture.
Just as the molar gas constant can be related to the Boltzmann constant, so can the specific gas constant by dividing the Boltzmann constant by the molecular mass of the gas.
Another important relationship comes from thermodynamics. Mayer’s relation relates the specific gas constant to the specific heat capacities for a calorically perfect gas and a thermally perfect gas.
where cp is the specific heat capacity for a constant pressure and cv is the specific heat capacity for a constant volume.[9]
It is common, especially in engineering applications, to represent the specific gas constant by the symbol R. In such cases, the universal gas constant is usually given a different symbol such as R to distinguish it. In any case, the context and/or unit of the gas constant should make it clear as to whether the universal or specific gas constant is being referred to. [10]
In case of air, using the perfect gas law and the standard sea-level conditions (SSL) (air density ρ0 = 1.225 kg/m3, temperature T0 = 288.15 K and pressure p0 = 101325 Pa), we have that Rair = P0/(ρ0T0) = 287.052874247 J·kg−1·K−1. Then the molar mass of air is computed by M0 = R/Rair = 28.964917 g/mol.[11]
U.S. Standard Atmosphere[edit]
The U.S. Standard Atmosphere, 1976 (USSA1976) defines the gas constant R∗ as:[12][13]
- R∗ = 8.31432×103 N⋅m⋅kmol−1⋅K−1 = 8.31432 J⋅K−1⋅mol−1.
Note the use of kilomoles, with the resulting factor of 1000 in the constant. The USSA1976 acknowledges that this value is not consistent with the cited values for the Avogadro constant and the Boltzmann constant.[13] This disparity is not a significant departure from accuracy, and USSA1976 uses this value of R∗ for all the calculations of the standard atmosphere. When using the ISO value of R, the calculated pressure increases by only 0.62 pascal at 11 kilometers (the equivalent of a difference of only 17.4 centimeters or 6.8 inches) and 0.292 Pa at 20 km (the equivalent of a difference of only 33.8 cm or 13.2 in).
Also note that this was well before the 2019 SI redefinition, through which the constant was given an exact value.
References[edit]
- ^ «2018 CODATA Value: molar gas constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «Proceedings of the 106th meeting» (PDF). 16–20 October 2017.
- ^ Jensen, William B. (July 2003). «The Universal Gas Constant R«. J. Chem. Educ. 80 (7): 731. Bibcode:2003JChEd..80..731J. doi:10.1021/ed080p731.
- ^ «Ask the Historian: The Universal Gas Constant — Why is it represented by the letter R?» (PDF).
- ^ Mendeleev, Dmitri I. (September 12, 1874). «An exert from the Proceedings of the Chemical Society’s Meeting on Sept. 12, 1874». Journal of Russian Chemical-Physical Society, Chemical Part. VI (7): 208–209.
- ^ Mendeleev, Dmitri I. (1875). On the elasticity of gases [Объ упругости газовъ]. A.M. Kotomin, St.-Petersburg.
- ^ D. Mendeleev. On the elasticity of gases. 1875 (in Russian)
- ^ Mendeleev, Dmitri I. (March 22, 1877). «Mendeleef’s researches on Mariotte’s law 1». Nature. 15 (388): 498–500. Bibcode:1877Natur..15..498D. doi:10.1038/015498a0.
- ^ Anderson, Hypersonic and High-Temperature Gas Dynamics, AIAA Education Series, 2nd Ed, 2006
- ^ Moran and Shapiro, Fundamentals of Engineering Thermodynamics, Wiley, 4th Ed, 2000
- ^ Manual of the US Standard Atmosphere (PDF) (3 ed.). National Aeronautics and Space Administration. 1962. pp. 7–11.
- ^ «Standard Atmospheres». Retrieved 2007-01-07.
- ^ a b NOAA, NASA, USAF (1976). U.S. Standard Atmosphere, 1976 (PDF). U.S. Government Printing Office, Washington, D.C. NOAA-S/T 76-1562.
{{cite book}}: CS1 maint: multiple names: authors list (link) Part 1, p. 3, (Linked file is 17 Meg)
External links[edit]
- Ideal gas calculator Archived 2012-07-15 at the Wayback Machine – Ideal gas calculator provides the correct information for the moles of gas involved.
- Individual Gas Constants and the Universal Gas Constant – Engineering Toolbox
Содержание:
- Уравнение состояния идеального газа
- Термодинамические параметры газа
- Объединенный газовый закон. Приведение объема газа к нормальным условиям
- Молярная газовая постоянная. Определение числового значения постоянной Больцмана
- Уравнение Клапейрона — Менделеева. Плотность газа
- Зависимость средней квадратичной скорости молекул газа от температуры
- Изохорический процесс
- Изобарический- процесс
- Изотермический процесс
- Внутренняя энергия идеального газа
- Работа газа при изменении его объема
Уравнение состояния идеального газа получило название «уравнение Менделеева-Клапейрона». Давление смеси химически невзаимодействующих газов равно сумме их парциальных давлений: закон Дальтона.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Уравнение состояния идеального газа
Уравнение состояния идеального газа — это p = nkT называется уравнением Менделеева Клапейрона и оно даёт взаимосвязь трёх важнейших макроскопических параметров, описывающих состояние идеального газа давления, объёма и температуры. Поэтому уравнение Менделеева Клапейрона называется ещё уравнением состояния идеального газа.
Термодинамические параметры газа
В предыдущих главах было показано, что при описании свойств газа можно пользоваться величинами, характеризующими молекулярный мир (микромир), например энергией молекулы, скоростью ее движения, массой и т. п. Числовые значения таких величин мы можем определять только с помощью расчета. Все такие величины принято называть микроскопическими (от греческого «микрос» — малый).
Однако для описания свойств газов можно пользоваться и такими величинами, числовые значения которых находят простым измерением с помощью приборов, например давлением, температурой и объемом газа. Значения таких величин определяются совместным действием огромного числа молекул, поэтому они называются макроскопическими (от греческого «макрос» — большой).
Соотношение (4.1):
Если взять определенную массу газа т, то при постоянных р, V и Т газ будет находиться в равновесном состоянии. Когда происходят изменения этих параметров, то в газе протекает тот или иной процесс. Если этот процесс состоит из ряда непрерывно следующих друг за другом равновесных состояний газа, то он называется равновесным процессом. Равновесный процесс должен протекать достаточно медленно, так как при быстром изменении параметров давление и температура не могут иметь соответственно одинаковые значения во всем объеме газа. В этой главе рассматриваются только равновесные процессы в газах, при которых масса газа остается постоянной.
Когда процесс в газе заканчивается, то газ переходит в новое состояние, а его параметры приобретают новые постоянные числовые значения, вообще говоря, отличные от их значений в начале процесса. Если же при постоянной массе газа значения всех его параметров в начале и в конце процесса окажутся одинаковыми, то процесс называется круговым или замкнутым.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом. Газовый закон, выражающий связь между всеми тремя параметрами газа, называется объединенным газовым законом.
Отметим еще, что такого процесса в газе, при котором изменялся бы только один параметр газа, не существует, так как значения этих параметров взаимосвязаны. Примером сказанного является закон Шарля, выражающий связь между р и Т.
Объединенный газовый закон. Приведение объема газа к нормальным условиям
Связь между давлением, объемом и температурой определенной массы газа устанавливается с помощью соотношения (4.9):
Поскольку 

Так как при постоянной массе газа N остается неизменным, 
Поскольку значения р, V и Т в (5.2) относятся к одному и тому же состоянию газа, можно следующим образом сформулировать объединенный газовый закон: при постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Следовательно, если числовые значения параметров в начале процесса, происходящего с какой-либо определенной массой газа, обозначить через р1 , V1 и Т1, а их значения в конце процесса соответственно через р2 , V2 и Т2, то
Формулы (5.2) и (5.3) представляют собой математическое выражение объединенного газового закона.
На практике иногда нужно установить, какой объем V0 займет имеющаяся масса газа при нормальных условиях, т. е. при Т0=273 К и при р0=1,013 . 105 Па. Если значения параметров для этой массы газа в каком-либо произвольном состоянии, отличном от нормального, обозначить через р, V и Т, то на основании (5.3) получаем 
Формула (5.4) позволяет приводить объем заданной массы газа к нормальным условиям.
Молярная газовая постоянная. Определение числового значения постоянной Больцмана
Формула (5.1) справедлива для любой массы газа, в которой содержится N молекул. Если применить эту формулу к одному молю какого-либо газа, то N нужно заменить постоянной Авогадро NA, а V — объемом одного моля Vмоль
Так как в одном моле любого газа содержится одно и то же число молекул NA, то произведение 

где
Числовое значение R можно найти, если применить (5.5) к состоянию одного моля газа при нормальных условиях, так как при этом 
где
Это числовое значение R в СИ необходимо запомнить, так как им часто пользуются при расчетах и при решении задач.
Теперь легко найти числовое значение постоянной Больнмана 



Уравнение Клапейрона — Менделеева. Плотность газа
Выясним, как будет выглядеть соотношение (5.1), если в него ввести молярную газовую постоянную R. Так как N — полное число молекул в массе газа т, а 
где 
Поскольку 


Соотношение (5.7) называется уравнением Клапейрона — Менделеева или уравнением состояния для произвольной массы идеального газа. Для одного моля идеального газа уравнение Клапейрона — Менделеева принимает вид
С помощью формулы (5.7) легко выяснить, какими величинами определяется плотность газа. Так как 
Зависимость средней квадратичной скорости молекул газа от температуры
Выясним теперь, как можно с помощью вычислений находить среднюю квадратичную скорость движения молекул газа 



Отметим, что под т в формуле (5.10) подразумевается масса одной молекулы в кг. Так как 



Наконец, из (5.9) следует, что 
Среднюю квадратичную скорость можно находить по любой из формул (5.10)—(5.12). Из функции Максвелла можно получить формулы для средней арифметической скорости и наивероятнейшей скорости. Средняя арифметическая скорость
Наконец, наивероятнейшую скорость вычисляют так:
(Используя график функции Максвелла (рис. 3.3), поясните, почему 


Изохорический процесс
Процессы, при которых масса газа и один из его параметров остаются постоянными, называются изопроцессами (от греческого «изос» — равный, одинаковый). Поскольку имеется три параметра газа, существует три различных изопроцесса. Первый из них (изохорический) рассмотрен выше (§ 4.3). Процесс в газе, который происходит при постоянной массе и неизменном объеме, называется изохорическим (от греческого «хора» — пространство). Графики для этого процесса называются изохорами (рис. 4.3).
Отметим, что к любому изопроцессу применим объединенный газовый закон и формулы (5.3), (5.7) и (5.8) с учетом того, что один из параметров остается постоянным. При изохорическом процессе постоянным остается объем V, поэтому формула (5.3) после сокращения на V принимает вид
Итак, изохорический процесс подчиняется закону Шарля: при постоянной-массе газа и неизменном объеме давление газа прямо пропорционально его абсолютной температуре. Это видно и из уравнения Клапейрона — Менделеева (5.7):
Так как V, т, 
Изобарический- процесс
Процесс в газе, который происходит при постоянной массе и неизменном давлении, называется изобарическим (от греческого «барос» — тяжесть). Этот процесс был изучен французским физиком Л. Гей-Люссаком в 1802 г.
Поскольку при изобарическом процессе р постоянно, то после сокращения на р формула (5.3) принимает вид
Формула (5.16) является математическим выражением закона Гей-Люссака: при постоянной массе газа и неизменном давлении объем газа прямо пропорционален его абсолютной температуре. (Это видно и из уравнения Клапейрона — Менделеева (5.7): так как р, т, 
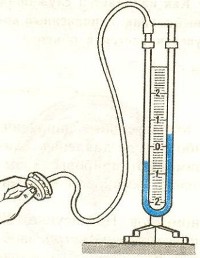
На рис. 5.1 схематически изображен опыт Гей-Люссака. Колба с газом помещается в сосуд с водой и льдом.
В пробку вставлена трубка, изогнутая таким образом, что свободный конец ее горизонтален. Газ в колбе отделен от окружающего воздуха небольшим столбиком ртути в трубке. Температуру газа определяют по термометру, а объем — по положению столбика ртути. Для этого на трубке нанесены деления, соответствующие определенному внутреннему объему трубки (при градуировке трубки можно учесть и расширение сосуда при нагревании, но оно сравнительно мало’).
Сначала по положению столбика ртути 1 определяют 
Оказывается, что изобара представляет собой прямую линию (рис. 5.2, а), которая пересекается с осью абсцисс в точке А.
Из подобия треугольников на рис. 5.2, а следует
Обозначив 

Здесь 
Если повторять этот опыт для разных газов или для разных масс газа, то все графики будут пересекаться в точке А, соответствующей t=—273°С (рис. 5.2, б), т. е. коэффициент 
Отметим, что для газов коэффициенты 


Изотермический процесс
Процесс в газе, который происходит при постоянной температуре, называется изотермическим.
Изотермический процесс в газе был изучен английским ученым Р. Бойлем и французским ученым Э. Мариоттом. Установленная ими опытным путем связь получается непосредственно из формулы (5.3) после сокращения на Т:
Формула (5.18) является математическим выражением закона Бойля — Мариотта: при постоянной массе газа и неизменной температуре давление газа обратно пропорционально его объему. Иначе говоря, в этих условиях произведение объема газа на соответствующее давление есть величина постоянная:
Соотношение (5.19) можно получить и из (5.7) или (5.8), так как при постоянном Г справа в формулах (5.7) и (5.8) стоит постоянная величина. График зависимости р от V при изотермическом процессе в газе представляет собой гиперболу и называется изотермой. На рис. 5.3 изображены три изотермы для одной и той же массы газа, но при разных температурах Т.
Отметим еще, что из формулы (5.9) непосредственно вытекает, что при изотермическом процессе плотность газа изменяется прямо пропорционально давлению:
(Подумайте, как проверить закон Бойля — Мариотта на опыте.)
Внутренняя энергия идеального газа
Как отмечалось, силы взаимодействия молекул в идеальном газе отсутствуют. Это означает, что молекулярно-потенциальной энергии у идеального газа нет. Кроме того, атомы идеального газа представляют собой материальные точки, т. е. не имеют внутренней структуры, а значит, не имеют и энергии, связанной с движением и взаимодействием частиц внутри атома. Таким образом, внутренняя энергия идеального газа представляет собой только сумму знамений кинетической энергии хаотического движения всех его молекул:
Поскольку у материальной точки вращательного движения быть не может, то у одноатомных газов (молекула состоит из одного атома) молекулы обладают только поступательным движением. Так как среднее значение энергии поступательного движения молекул определяется соотношением(4.8): 



Для произвольной массы одноатомного идеального газа имеем
Если молекула газа состоит из двух жестко связанных атомов (двухатомный газ), то молекулы при хаотическом движении приобретают еще и вращательное движение, которое происходит вокруг двух взаимно перпендикулярных осей. Поэтому при одинаковой температуре внутренняя энергия двухатомного газа больше, чем одноатомного, и выражается формулой
Наконец, внутренняя энергия многоатомного газа (молекула содержит три или больше атомов) в два раза больше, чем у одно-атомного при той же температуре:
поскольку вращение молекулы вокруг трех взаимно перпендикулярных осей вносит в энергию теплового движения такой же вклад, как поступательное движение молекулы по трем взаимно перпендикулярным направлениям.
Отметим, что формулы (5.23) и (5.24) теряют силу для реальных газов при высоких температурах, так как при этом в молекулах возникают еще колебания атомов, что ведет к увеличению внутренней энергии газа. (Почему это не относится к формуле (5.22)?)
Работа газа при изменении его объема
Физический смысл молярной газовой постоянной. Опыт показывает, что сжатый газ в процессе своего расширения может выполнять работу. Приборы и агрегаты, действия которых основаны на этом свойстве газа, называют пневматическими. На этом принципе действуют пневматические молотки, механизмы для закрывания и открывания дверей на транспорте и т. д.
Представим себе цилиндр с подвижным поршнем, заполненный газом (рис. 5.4).
Пока давление газа внутри цилиндра и окружающего наружного воздуха одинаковы, поршень неподвижен. Пусть при этом температура газа и окружающей среды равна 
Будем теперь медленно нагревать газ в цилиндре до температуры 






Нетрудно сообразить, что при изохорическом процессе работа газа равна нулю, так как никакого изменения объема, занятого газом, в этом случае не происходит. Вообще следует помнить, что газ выполняет работу только в процессе изменения своего объема, т. е. при 


Выясним, как можно определить работу газа по графику зависимости р от V в том или ином газовом процессе. При изобарическом процессе график зависимости р от V представляет собой прямую линию, параллельную оси абсцисс, так как р постоянно. Из рис. 5.5 видно, что работа газа в этом случае численно равна заштрихованной площади.
Выясним, как найти работу газа при изотермическом процессе. На рис. 5.6 изображена изотерма идеального газа. При таком процессе газ выполняет работу, так как 




Разбивая интервал 





Можно строго доказать, что работа газа при любом процессе выражается площадью, ограниченной двумя ординатами, отрезком оси абсцисс и графиком того процесса в координатах V и р.
Выясним теперь физический смысл молярной газовой постоянной R. Применяя формулу (5.25) к одному молю идеального газа, получим
Но из уравнения Клапейрона — Менделеева (5.8) для одного моля можно записать для двух состояний газа:
откуда
Подставляя это выражение в (5.26), будем иметь 
Из (5.27) следует, что молярная газовая постоянная численно равна работе, совершаемой одним молем идеального газа при его изобарическом нагревании на один кельвин.
Из соотношения 
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно — кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
lab12.pdf
Скачиваний:
9
Добавлен:
03.03.2016
Размер:
170.99 Кб
Скачать
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ Государственное высшее учебное заведение
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра физики
ОТЧЕТ по лабораторной работе №12
ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ ГАЗОВОЙ ПОСТОЯННОЙ МЕТОДОМ ОТКАЧКИ
Выполнил студент группы_________________
________________________________________
Преподаватель кафедры физики
________________________________________
Отметка о защите_________________________
2011
|
Волков А.Ф., Лумпиева Т.П. |
Физический практикум |
Лабораторная работа № 12
ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ ГАЗОВОЙ ПОСТОЯННОЙ МЕТОДОМ ОТКАЧКИ
Цель работы: определить молярную газовую постоянную.
Приборы и принадлежности: сосуд с зажимом, насос Комовского, вакуумметр, аналитические весы, разновесы.
Общие положения
Молярная газовая постоянная R – универсальная физическая постоянная, входящая в уравнение состояния. Молярная газовая постоянная численно равна работе расширения 1 моля идеального газа под постоянным давлением при нагревании на 1 К.
Один из методов определения R основан на использовании уравнения состояния идеального газа:
|
pV = |
m |
RT , |
(1) |
|
|
M |
||||
|
где p − давление газа; |
||||
|
V − объем, занимаемый данной массой газа; |
||||
|
m − масса газа; |
||||
|
T − абсолютная температура; |
||||
|
M − молярная масса. |
||||
|
Взвесим сосуд с воздухом при атмосферном давлении pатм = p1 . |
Запишем |
|||
|
уравнение Менделеева − Клапейрона для первого состояния: |
||||
|
p V = |
m1 −m0 |
RT |
(2) |
|
|
1 |
M |
|||
где V − внутренний объем сосуда; m1 − масса сосуда с воздухом; m0 − собственная масса сосуда;
M − молярная масса воздуха, равная 29 10−3 кг/моль.
Соединим сосуд с вакуумметром и откачаем воздух. Запишем уравнение Менделеева − Клапейрона для второго состояния:
|
p V = |
m2 −m0 |
RT |
(3) |
|
2 |
M |
||
где p2 − давление в сосуде после откачки;
m2 − масса сосуда с воздухом после откачки. Вычтем из уравнения (2) уравнение (3):
|
(p |
− p |
2 |
)V = |
m1 −m2 |
RT |
(4) |
|
1 |
M |
|||||
1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Физическая постоянная, эквивалентная постоянной Больцмана, но в других единицах измерения
| Значения R | Единицы |
|---|---|
| Единицы СИ | |
| 8,31446261815324 | J ⋅K ⋅моль |
| 8,31446261815324 | m ⋅Pa ⋅K ⋅моль |
| 8,31446261815324 | kg ⋅m ·K ⋅моль s |
| 8,31446261815324 × 10 | L ⋅Pa ⋅K ⋅моль |
| 8,31446261815324 × 10 | L ⋅бар ⋅K ⋅моль |
| Стандартные единицы США | |
| 0,730240507295273 | атм ⋅ft ⋅lb ⋅моль °R |
| 10,731557089016 | psi ⋅ft ⋅⋅lb ⋅моль °R |
| 1.985875279009 | БТЕ ⋅⋅lb ⋅моль °R |
| Другие стандартные единицы | |
| 297.049031214 | дюйм. H 2O ⋅ft ⋅lb ⋅моль °R |
| 554.984319180 | торр ⋅ft ⋅lb ⋅моль °R |
| 0,082057366080960 | L ⋅атм ⋅K ⋅моль |
| 62,363598221529 | L ⋅торр ⋅K ⋅моль |
| 1.98720425864083… × 10 | ккал ⋅K ⋅моль |
| 8,20573660809596… × 10 | m ⋅атм ⋅K ⋅моль |
| 8,31446261815324 × 10 | эрг ⋅K ⋅моль |
Газовая постоянная (также известная как молярная газовая постоянная, универсальная газовая постоянная или идеальная газовая постоянная ) обозначается символом R или R. Это эквивалентно постоянная Больцмана, но выраженная в единицах энергии на приращение температуры на моль, то есть произведение давление-объем, а не энергия на приращение температуры на частицу. Константа также представляет собой сочетание констант из закона Бойля, закона Чарльза, закона Авогадро и закона Гей-Люссака. Это физическая константа, которая используется во многих фундаментальных уравнениях в физических науках, таких как закон идеального газа, уравнение Аррениуса и Уравнение Нернста.
Физически газовая постоянная — это константа пропорциональности, которая связывает энергетическую шкалу в физике с температурной шкалой, когда рассматривается моль частиц при указанной температуре. Таким образом, значение газовой постоянной в конечном итоге определяется историческими решениями и случайностями при установке шкалы энергии и температуры, а также аналогичной исторической установкой значения молярной шкалы, используемой для подсчета частиц. Последний фактор не учитывается при значении постоянной Больцмана, которая выполняет аналогичную работу по уравниванию линейной шкалы энергии и температуры.
Газовая постоянная R определяется как постоянная Авогадро NA, умноженная на постоянную Больцмана (kBили k):
- R = NA k, { displaystyle R = N _ { rm {A}} k _ {,} ,}
После изменения определения базовых единиц СИ в 2019 г., которое вступило в силу 20 мая 2019 г., оба N A и k определяются с помощью точных числовых значений, выраженных в единицах СИ. Как следствие, значение газовой постоянной также точно определено и составляет 8,31446261815324 Дж⋅К⋅моль.
Некоторые предположили, что было бы уместно назвать символ R константой Рено в честь французского химика Генри Виктор Реньо, чьи точные экспериментальные данные были использованы для расчета начального значения постоянной; однако происхождение буквы R, обозначающей константу, неуловимо.
Газовая постоянная встречается в законе идеального газа следующим образом:
- PV = n RT = m R удельное T { displaystyle PV = nRT = mR _ { rm {specific}} T}
где P — абсолютное давление (единица СИ паскали), V — объем газа (единица СИ кубическая метров), n — количество газа (моль единицы СИ), m — масса (единица СИ килограммы), содержащаяся в V, а T — термодинамическая температура (единица СИ кельвин). R specific — удельная газовая постоянная. Газовая постоянная выражается в тех же физических единицах, что и молярная энтропия и молярная теплоемкость.
Содержание
- 1 Размеры
- 2 Связь с постоянной Больцмана
- 3 Измерение и замена на заданное значение
- 4 Удельная газовая постоянная
- 5 Стандартная атмосфера США
- 6 Ссылки
- 7 Внешние ссылки
Размеры
Из закона идеального газа PV = nRT получаем:
- R = PV n T { displaystyle R = { frac {PV} {nT}}}
где P — давление, V — объем, n — количество молей данного вещества, а T — температура.
Поскольку давление определяется как сила на единицу площади, уравнение газа также можно записать как:
- R = силовая площадь × объем × температура { displaystyle R = { frac {{ dfrac { mathrm {force}} { mathrm {area}}} times mathrm {volume}} { mathrm {amount} times mathrm {temperature}}}}
Площадь и объем — это (длина) и (длина) соответственно. Следовательно:
- R = сила (длина) 2 × (длина) 3 величина × температура = сила × длина, высота × температура { displaystyle R = { frac {{ dfrac { mathrm {force}} {( mathrm { length}) ^ {2}}} times ( mathrm {length}) ^ {3}} { mathrm {amount} times mathrm {temperature}}} = { frac { mathrm {force} times mathrm {length}} { mathrm {amount} times mathrm {temperature}}}}
Поскольку сила × длина = работа:
- R = рабочее количество × температура { displaystyle R = { frac { mathrm {work}} { mathrm {amount} times mathrm {temperature}}}}
Физическое значение R — работа на градус на моль. Он может быть выражен в любом наборе единиц, представляющих работу или энергию (например, джоулей ), единицах, представляющих градусы температуры по абсолютной шкале (например, Кельвин или Ранкина ), и любая система единиц, обозначающая моль или подобное чистое число, которое позволяет уравнение макроскопической массы и чисел фундаментальных частиц в системе, такой как идеальный газ (см. постоянная Авогадро ).
Вместо моля постоянную можно выразить, рассматривая нормальный кубический метр.
В противном случае мы также можем сказать, что:
- сила = масса × длина (время) 2 { displaystyle mathrm {force} = { frac { mathrm {mass} times mathrm {length}} {( mathrm {time}) ^ {2}}}}
Следовательно, мы можем записать R как:
- R = масса × длина 2 количество × температура × (время) 2 { displaystyle R = { frac { mathrm {mass} times mathrm {length} ^ {2}} { mathrm {amount} times mathrm {температура} times ( mathrm {time}) ^ {2}}}}
Итак, в основных единицах СИ :
- R = 8,314462618… кг⋅м⋅с⋅K ⋅mol.
Связь с постоянной Больцмана
Постоянная Больцмана kB(часто сокращенно k) может использоваться вместо газовой постоянной, работая с чистым подсчетом частиц N, а чем количество вещества, n, поскольку
- R = NA k B, { displaystyle R = N _ { rm {A}} k _ { rm {B}}, ,}
где N — это константа Авогадро. Например, закон идеального газа в терминах постоянной Больцмана равен
- P V = k B N T. { displaystyle PV = k _ { rm {B}} NT.}
где N — количество частиц (в данном случае молекул), или, если обобщить на неоднородную систему, локальная форма имеет место:
- P = k B n T. { displaystyle P = k _ { rm {B}} nT.}
где n — числовая плотность.
Измерение и замена заданным значением
По состоянию на 2006 г. Измерение R было получено путем измерения скорости звука ca(P, T) в аргоне при температуре T тройной точки воды при различных давления P и экстраполяция до предела нулевого давления c a (0, T). Затем значение R получается из соотношения
- ca (0, T) = γ 0 RTA r (A r) M u, { displaystyle c _ { mathrm {a}} (0, T) = { sqrt { frac { gamma _ {0} RT} {A _ { mathrm {r}} ( mathrm {Ar}) M _ { mathrm {u}}}}},}
где:
- γ0- коэффициент теплоемкости (⁄ 3 для одноатомных газов, например аргона);
- T — температура, T TPW = 273,16 K по определению кельвина;
- Ar(Ar) — относительная атомная масса аргона, а M u = 10 кг⋅моль.
Однако после переопределения СИ в 2019 базовые единицы, R теперь имеет точное значение, определенное в терминах других точно определенных физических констант.
Удельная газовая постоянная
| Rудельная. для сухого воздуха | Единицы |
|---|---|
| 287,058 | Дж⋅кг⋅К |
| 53,3533 | фут⋅ фунт-сила ⋅lb ⋅ ° R |
| 1716,49 | фут⋅ фунт-сила ⋅ снаряд ⋅ ° R |
| На основе при средней молярной массе. для сухого воздуха 28,9645 г / моль. |
удельная газовая постоянная газа или смеси газов (R удельная) дается как молярная газовая постоянная, деленная на молярную массу ( M) газа или смеси.
- R specific = RM { displaystyle R _ { rm {specific}} = { frac {R} {M}}}
Так же, как постоянная идеального газа может быть связана с постоянной Больцмана, удельную газовую постоянную путем деления постоянной Больцмана на молекулярную массу газа.
- R s p e c я е я c = k B m { displaystyle R _ { rm {specific}} = { frac {k _ { rm {B}}} {m}}}
Еще одно важное соотношение исходит из термодинамики. Соотношение Майера связывает удельную газовую постоянную с удельной теплотой для калорийно совершенного газа и термически совершенного газа.
- R specific = cp — cv { displaystyle R _ { rm {specific}} = c _ { rm {p}} — c _ { rm {v}} }
где c p — это удельная теплоемкость для постоянного давления, а c v — удельная теплоемкость для постоянного объема.
Обычно, особенно в инженерных приложениях, чтобы обозначить удельную газовую постоянную символом R. В таких случаях универсальной газовой постоянной обычно присваивается другой символ, например R. В любом случае контекст и / или единицы измерения газовой постоянной должны указывать на то, идет ли речь о универсальной или специальной газовой постоянной.
США Стандартная атмосфера
США Стандартная атмосфера, 1976 (USSA1976) определяет газовую постоянную R как:
- R = 8,31432 × 10 Н⋅м⋅кмоль⋅К.
Обратите внимание на использование киломолей, дающее коэффициент 1000 в постоянный. USSA1976 признает, что это значение не согласуется с приведенными значениями для постоянной Авогадро и постоянной Больцмана. Это несоответствие не является существенным отклонением от точности, и USSA1976 использует это значение R для всех расчетов стандартной атмосферы. При использовании значения R ISO расчетное давление увеличивается всего на 0,62 паскаль на расстоянии 11 километров (что эквивалентно разнице всего в 17,4 см или 6,8 дюйма) и на 0,292. Па на 20 км (эквивалент разницы всего в 33,8 см или 13,2 дюйма).
Также обратите внимание, что это было задолго до переопределения SI 2019 года, которое дало константе точное значение.
Ссылки
Внешние ссылки
- Калькулятор идеального газа — Калькулятор идеального газа предоставляет правильную информацию для соответствующих молей газа.
- Индивидуальные газовые постоянные и универсальные газовые постоянные — Engineering Toolbox
Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.
Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:
- все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
- частицы находятся в непрерывном тепловом движении;
- между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.
Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.
Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.
Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.
Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.
Существует еще одно состояние вещества – плазма. Плазма — частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е. молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
Модель идеального газа. Связь между давлением и средней кинетической энергией.
Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.
Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)
Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.
Свойства идеального газа:
- расстояние между молекулами много больше размеров молекул;
- молекулы газа очень малы и представляют собой упругие шары;
- силы притяжения стремятся к нулю;
- взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
- молекулы этого газа двигаются беспорядочно;
- движение молекул по законам Ньютона.
Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.
Объем газа обозначается V. Объем газа всегда совпадает с объемом того сосуда, который он занимает. Единица объема в СИ м3.
Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.
p = F/S Единица давления в СИ паскаль [Па]
До настоящего времени употребляются внесистемные единицы давления:
техническая атмосфера 1 ат = 9,81-104 Па;
физическая атмосфера 1 атм = 1,013-105 Па;
миллиметры ртутного столба 1 мм рт. ст.= 133 Па;
1 атм = = 760 мм рт. ст. = 1013 гПа.
Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени действует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.
Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.
Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.
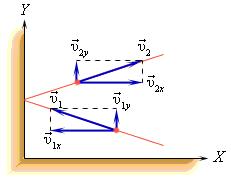
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной.
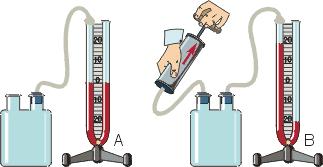
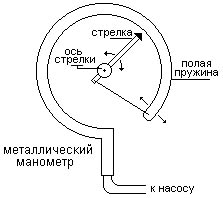
Приборы, измеряющие давление, называют манометрами. Манометры фиксируют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.
Жидкостные манометры:
- открытый – для измерения небольших давлений выше атмосферного
- закрытый — для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума

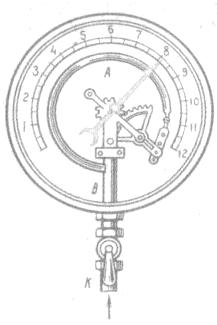
Металлический манометр – для измерения больших давлений.
Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.
Основное уравнение молекулярно-кинетической теории идеального газа.
Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул
p = 1/3·m0·n·v2
m0 — масса одной молекулы газа;
n = N/V – число молекул в единице объема, или концентрация молекул;
v2 — средняя квадратичная скорость движения молекул.
Так как средняя кинетическая энергия поступательного движения молекул E = m0*v2/2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0· v2)/2 = 2/3·E·n
p = 2/3·E·n
Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
Так как m0·n = m0·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v2
Объединенный газовый закон.
Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Всякое изменение состояния газа называется термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.
Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
p = nkT
Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим или
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.
Уравнение Клайперона можно записать в другой форме.
p = nkT,
учитывая, что
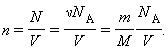
Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
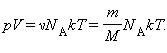
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
Ее численное значение в СИ R = 8,31 Дж/моль·К
Соотношение
называется уравнением состояния идеального газа.
В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`
Для одного моля любого газа это соотношение принимает вид: pV=RT
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.
Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pSΔh = R
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A.
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.