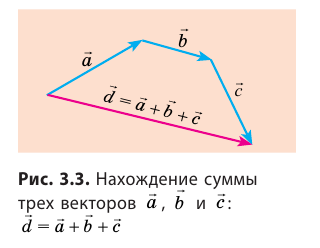
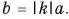Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
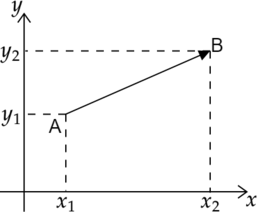
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
На рис. 1.1:
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
Правило сложения векторов
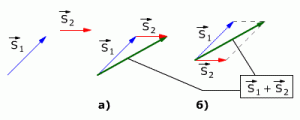
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
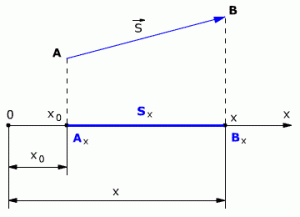
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения (см.рис. 1.3).
Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
Sx = AxBx
ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть
Sx = x – x0
Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
Sy = y – y0 Sz = z – z0
Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).
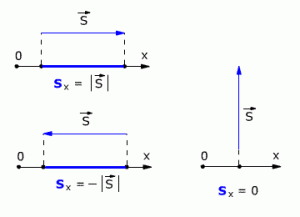
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
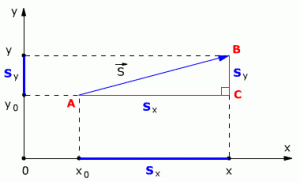
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
Sx = x – x0 Sy = y – y0
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
АС = sx CB = sy
По теореме Пифагора
S2 = Sx2 + Sy2
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.
2.1. Теорема Пифагора
Прямоугольный треугольник — треугольник, в котором один из углов прямой (то есть равен 90°). Сторона, противолежащая прямому углу, называется гипотенузой. Стороны, образующие прямой угол, называются катетами (см. рис.).
Для любого прямоугольного треугольника справедлива теорема Пифагора:
Гипотенузу можно найти по формуле:
Катет можно найти по формуле:
2.2 Как найти и
из прямоугольного треугольника?
Рассмотрим прямоугольный треугольник с катетами a и b и гипотенузой c. Обозначим через α угол, лежащий напротив катета a (см. рис.).
Тогда, катет a — противолежащий катет для угла α (лежит напротив угла); катет b — прилежащий катет (непосредственно образует угол).
Синус угла α — отношение противолежащего катета к гипотенузе:
Косинус угла α — отношение прилежащего катета к гипотенузе:
Тангенсом угла α — отношение противолежащего катета к прилежащему:
2.3 Как найти проекции вектора, если известен его модуль и направление?
1) Опускаем перпендикуляры на ось Ox и ось Oy;
2) Проекции равны:
3) Правило знаков.
Пусть даны вектор и ось Ox. Из начала и конца вектора
опустим перпендикуляры на ось Ox. Пусть A и B — основания этих перпендикуляров (см. рис.).
Проекция вектора
на ось Ox (Oy) равна длине отрезка AB, взятой со знаком плюс, если угол φ между вектором
и осью Ox (Oy) является острым, и взятой соответственно со знаком минус, если φ тупой (или развернутый). Если угол φ прямой, то
То есть:
Получаем:
2.4 Как найти проекции вектора, если известны координаты начала и конца вектора?
Пусть и
) — координаты начала и конца вектора соответственно. Тогда проекции
2.5 Как найти модуль вектора, если известны его проекции на оси?
Если известны проекции вектора и
на оси координат, то модуль вектора легко найти по формуле:
2.6 Как найти модуль вектора, если известны координаты конца и начала вектора?
Пусть и
— координаты начала и конца вектора
соответственно. Тогда модуль вектора находится по формуле:
2.7 Теорема косинусов.
Для треугольника со сторонами a, b и c, углом α справедлива теорема:
2.8 Как сложить вектора, направленные вдоль одной прямой?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.).
Из рисунка видно, что модуль вектора равен:
2.9 Как вычитать вектора, направленные вдоль одной прямой?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.). Вектор
— это вектор, длина которого равна длине вектора
, но имеет противоположное направление.
Из рисунка видно, что модуль вектора равен:
2.10 Как сложить вектора, направленные под прямым углом друг к другу?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.).
Из рисунка видно, что модуль вектора равен:
2.11 Как вычитать вектора, направленные под прямым углом друг к другу?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.). Вектор
— это вектор, длина которого равна длине вектора
но имеет противоположное направление.
Из рисунка видно, что модуль вектора равен:
2.12 Как сложить вектора, направленные под углом α друг к другу?
Пусть даны вектора и
, имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.).
По теореме косинусов, получаем:
2.13 Как вычитать вектора, направленные под прямым углом друг к другу?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.). Вектор
— это вектор, длина которого равна длине вектора
, но имеет противоположное направление.
По теореме косинусов, получаем:
2.14 Площадь треугольника.
Площадь любого треугольника можно найти по формуле
2.15 Площадь прямоугольника.
Площадь любого прямоугольника можно найти по формуле
2.16 Площадь трапеции.
Площадь любой трапеции можно найти по формуле
2.17 Длина окружности.
Длина окружности равна:
2.18 Длина дуги.
Длина дуги:
Закрепленный вектор — упорядоченная пара точек (направленный отрезок, имеющий начало и конец).
Обозначать можем следующими способами: (overrightarrow{AB}), где (A) — начало, а (B) — конец вектора или просто (vec{a}).
Длина вектора — расстояние между началом и концом вектора.
Длина векторов обозначается следующим образом: (|vec{a}|) или (|overrightarrow{AB}|).
Если задана прямоугольная система координат, и координаты начала и конца вектора заданы в ней парами (A=(x_1,y_1)) и (B=(x_2,y_2)) соответственно, тогда координаты вектора можно задать [overrightarrow{AB}={,x_2-x_1, y_2-y_1,}]
Тогда длина вектора (overrightarrow{AB}) задается формулой
[|overrightarrow{AB}|=sqrt{(x_2-x_1)^2-(y_2-y_1)^2}]
Проекцией вектора на какую-либо ось называется длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком <<(displaystyle +)>> или <<(displaystyle -)>>.
Например, проекцией вектора (overrightarrow {AB}) на ось можно считать отрезок (displaystyle A’B’), взятый со знаком <<+>>.
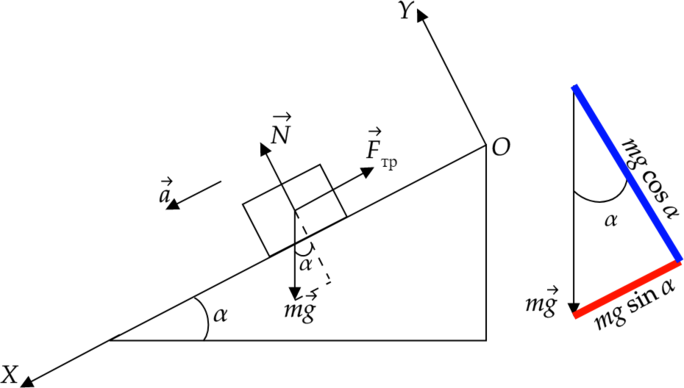
Рассмотрим ситуацию, когда брусок движется по наклонной плоскости:
Исходя из рисунка мы можем записать II закон Ньютона в векторной форме: [vec{F}_text{тр}+mvec{g}+vec{N}=mvec{a}]
Запишем теперь проекции на оси:
[OY:-mgcosalpha+N=0] [OX:-F_text{тр}+mgsinalpha=ma]
Посмотрим, как получили два вышеприведенных равенства. Направим оси, как на рисунке, тогда по оси (OY) ускорение и сила трения на тело не действуют, так как они направлены перпендикулярно этой оси, а проекции сил, перпендикулярных оси, равны нулю.
Сила реакции опоры направлена по оси (OY), значит, возьмем ее положительную проекцию.
Также рассмотрим силу тяжести, вектор которой НЕ КОЛЛИНЕАРЕН осям координат, разложим его на два составляющие (см. рисунок сбоку) и возьмем синюю линию, являющуюся проекцией силы тяжести на ось (OY). Из простых геометрических соображений видим, что она равна (-mgcosalpha).
Аналогично действуем для оси (OX).
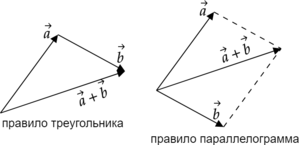
Сложение векторов можно производить по правилу треугольника или по правилу параллелограмма, рассмотрим на примере.
Даны векторы (vec{a}) и (vec{b}), по правилу треугольника мы можем получить сумму (vec{a}+vec{b}), совместив конец вектора (vec{a}) с началом вектора (vec{b}).
Даны векторы (vec{a}) и (vec{b}), по правилу параллелограмма мы можем получить сумму (vec{a}+vec{b}), совместив начало вектора (vec{a}) с началом вектора (vec{b}).
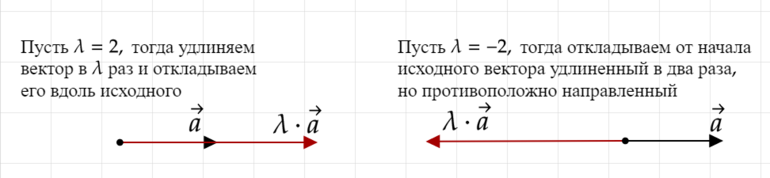
Умножение вектора на число.
Рассмотрим различные варианты произведения вектора (vec{a}) на какое-то вещественное число (lambda):
1) (lambda=0)
[vec{a}cdot0=vec{0}]
При умножении на нулевое число получается нулевой вектор (вектор нулевой длины);
2) (lambda>0)
При умножении на положительное число получается вектор, сонапаравленный исходному вектору (происходит просто “удлинение” или “укорачивание” нашего вектора, направление не меняется);
3) (lambda<0)
При умножении на отрицательное число получается вектор, противоположно направленный исходному вектору (происходит “разворот” вектора на 180 градусов и изменение его длины одновременно).
Скалярное произведение
Скалярным произведением векторов называют число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение скалярного произведения векторов (vec{a}) и (vec{b}) имеет вид ((vec{a},vec{b})=|vec{a}|cdot|vec{b}|cdotcosBig(widehat{vec{a},vec{b}}Big))
Физический смысл скалярного произведения
Работу (A) тела, перемещаемого из точки (M) в (N) с постоянной силой (vec{F}), можно найти как произведение длин векторов (vec{F}) и (overrightarrow{MN}) с косинусом угла между ними, значит работа равна скалярному произведению векторов силы и перемещения:
[A=Big(vec{F},overrightarrow{MN}Big)]
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Содержание:
Скалярные и векторные величины:
В 7-м и 8-м классах мы рассматривали различные физические величины. Для одних величин достаточно знать их числовое значение и единицу измерения. Например, масса
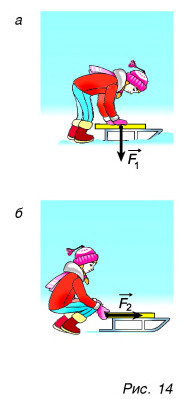
На рисунках 14, а и 14, б девочка действует на санки силой, имеющей одно и то же числовое значение. Но в первом случае санки лишь немного погрузились в снег, а во втором — пришли в движение. Значит, сила определяется не только числовым значением, но и направлением. Сила — величина векторная.
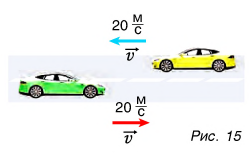
Векторной величиной является и скорость движения тел (рис. 15), и многие другие физические величины.
Что нужно знать о векторных величинах (векторах)
Векторы характеризуются модулем и направлением в пространстве
Модулем вектора называется его числовое значение.
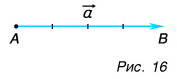
Вектор изображают в виде направленного отрезка (стрелки). Стрелка указывает, куда направлен вектор (рис. 14, 15). Длина стрелки характеризует модуль вектора (рис. 16). Над буквенным обозначением вектора ставят стрелку, например: 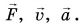
Модуль вектора обозначают той же буквой, но без стрелки над ней или символом 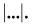
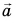
Модуль любого (не равного нулю) вектора — число положительное.
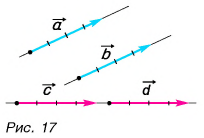
Векторы равны между собой, если равны их модули и одинаковы направления
Равные векторы лежат на одной и той же прямой или на параллельных прямых и направлены в одну и ту же сторону. На рисунке 17 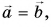
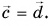
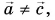
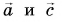
Угол между векторами
Чтобы найти угол 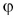
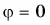
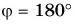
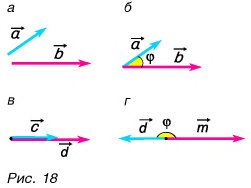
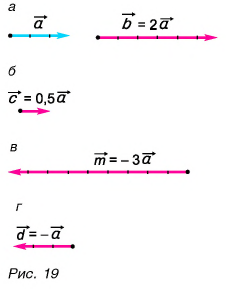
Умножение вектора на число
Произведение вектора 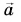
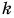
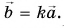
Модуль вектора 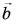
Если 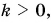
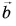
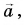
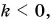
На рисунке 19 
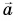
Противоположные векторы
Вектор 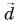
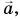
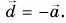
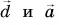
Сложение векторов
В 7-м классе вы складывали силы, направленные или одинаково, или в противоположные стороны. Результатом сложения в первом случае была сила, модуль которой равен 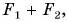
То же самое получается и при сложении векторов 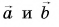
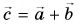
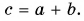
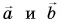
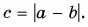
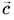
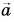
А как сложить векторы, направленные под любым углом друг к другу? Для этого можно использовать любое из двух следующих далее правил.
Правило параллелограмма
Совместим начала векторов 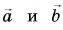
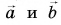
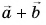
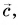
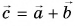
Правило треугольника
Совместим конец вектора 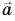
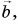
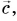
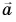
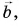
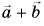
Из рисунков 21, б и 21, в ясно, что правило треугольника и правило параллелограмма дают одинаковые результаты. А как найти разность векторов?
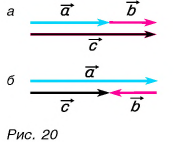
Вычитание векторов
Пусть начала векторов 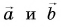
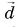
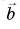
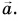
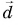
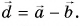
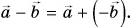
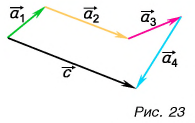
Правило многоугольника
Чтобы найти сумму нескольких векторов (например, 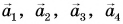
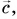
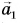
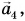
Правило многоугольника следует из правила треугольника.
Модуль суммы векторов
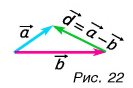
Не путайте модуль суммы векторов, т. е. 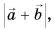
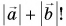
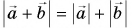
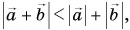
Нуль-вектор
Пусть вектор 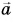
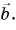
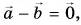
Главные выводы:
- Векторные величины характеризуются модулем и направлением, скалярные — только числовым значением.
- Сумму двух векторов находят по правилу параллелограмма или треугольника.
- Разность двух векторов находят, проводя вектор из конца вычитаемого вектора в конец уменьшаемого (при совмещенных началах векторов).
- Разность векторов
можно найти как сумму
- Произведение вектора
на число
есть вектор
При
направления векторов
совпадают, а при
— противоположны. Модуль вектора
равен
Скалярные и векторные величины
К пониманию того, что для описания природы нужно использовать язык математики, ученые пришли давно. Собственно, некоторые разделы математики и были созданы для того, чтобы описывать природу кратким и доступным языком. Так, для определения мгновенной скорости, работы переменной силы, объема тел неправильной формы и т. д. были созданы дифференциальное и интегральное исчисления. Для более наглядного описания физических процессов научились строить графики функций, а для быстрой обработки результатов эксперимента придумали методы приближенных вычислений. Вспомним скалярные и векторные величины, без которых вам не обойтись при изучении курса физики 10 класса.
Физические величины, используемые в физике для количественной характеристики физических явлений и объектов, делятся на два больших класса: скалярные величины и векторные величины.
К скалярным величинам, или скалярам (от лат. scalaris — ступенчатый), относятся величины, которые определяются только значением. Например, масса тела — скалярная величина, и если мы говорим, что масса тела равна двум килограммам (m=2 кг), то полностью определяем эту величину. Сложить две скалярные физические величины означает сложить их значения, представленные в одинаковых единицах. Понятно, что складывать можно только однородные скаляры (например, нельзя складывать массу и время, плотность и работу и т. д.).
Для определения векторных величин важно знать не только их значения, но и направления. Вектор (от лат. vector — носитель) — это направленный отрезок, то есть отрезок, имеющий и длину, и направление. Длину направленного отрезка называют модулем вектора. Обозначают векторные величины буквами греческого и латинского алфавитов, над которыми ставят стрелки, или полужирными буквами. Например, скорость записывают так: v или 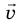
Правила сложения (вычитания) векторов отличаются от правил сложения (вычитания) скалярных величин.
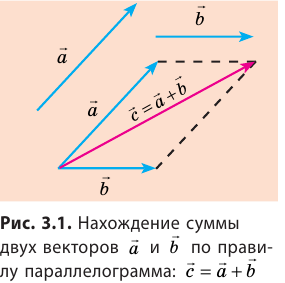
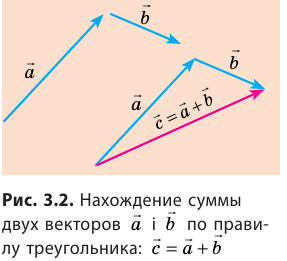
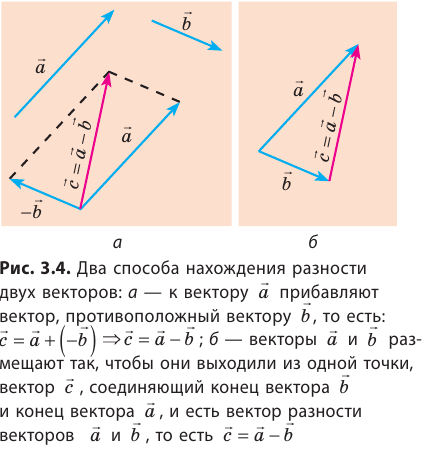
Сумму двух векторов находят по правилу параллелограмма или по правилу треугольника (рис. 3.1, 3.2). Как найти сумму нескольких векторов, показано на рис. 3.3, как найти разность двух векторов, показано на рис. 3.4.
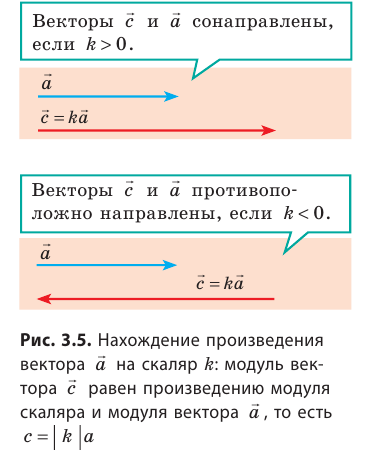
В результате умножения векторной величины 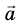
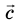
Обратите внимание! Единица произведения векторной и скалярной величин определяется как произведение единицы одной величины на единицу другой. Например, нужно найти перемещение самолета, который в течение 0,5 ч летит на север со скоростью 500 км/ч. Вектор перемещения: 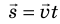
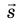
- Заказать решение задач по физике
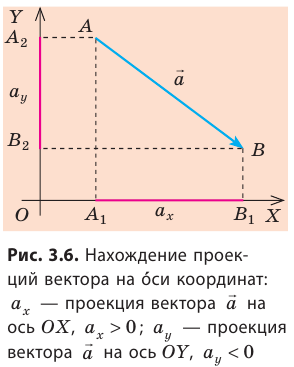
Как найти проекции вектора на оси координат
Осуществлять математические операции с векторами гораздо сложнее, чем со скалярами, поэтому, решая задачи, от векторных физических величин переходят к их проекциям на оси координат.
Пусть вектор 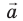
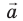
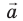
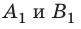
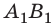
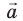
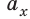
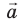
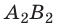
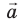
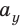
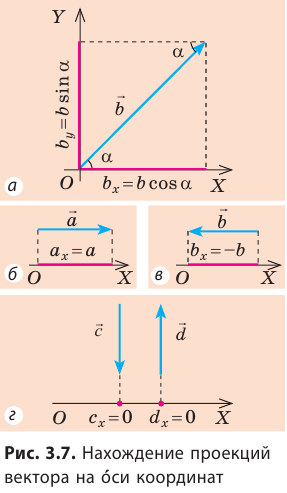
В общем случае проекцию вектора находят обычными геометрическими методами (рис. 3.7, а). На практике часто приходится иметь дело со случаями, когда вектор параллелен или перпендикулярен оси координат.
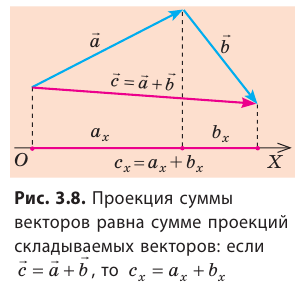
Если вектор параллелен оси координат, а его направление совпадает с направлением оси, то его проекция на эту ось положительна и равна модулю вектора (рис. 3.7, б). Если направление вектора противоположно направлению оси координат, то его проекция на эту ось равна модулю вектора, взятому с противоположным знаком (рис. 3.7, в). Если же вектор перпендикулярен оси координат, то его проекция на эту ось равна нулю (рис. 3.7, г). Очень важным свойством проекций является то, что проекция суммы двух векторов (рис. 3.8) или нескольких векторов на координатную ось равна алгебраической сумме проекций этих векторов на данную ось.
Именно это свойств позволяет заменять в уравнении векторные величины их проекциями — скалярными величинами и далее решать полученное уравнение обычными алгебраическими методами.
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники














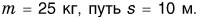
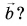
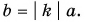
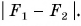

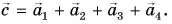
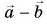 можно найти как сумму
можно найти как сумму 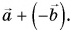
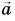 на число
на число 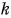 есть вектор
есть вектор 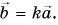 При
При 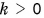 направления векторов
направления векторов 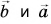 совпадают, а при
совпадают, а при 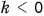 — противоположны. Модуль вектора
— противоположны. Модуль вектора 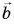 равен
равен