Содержание:
- Формула
- Примеры вычисления модуля вектора
Формула
Чтобы найти модуль вектора, заданного своими координатами, нужно найти его длину, то есть извлечь корень из суммы
квадратов его координат. Если вектор задан на плоскости и имеет координаты $bar{a}=left(a_{x} ; a_{y}right)$, то его модуль вычисляется по формуле
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}$$
То есть модуль вектора равен корню квадратному из суммы квадратов координат.
Если вектор задан в пространстве координатами
$$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$$
Примеры вычисления модуля вектора
Пример
Задание. Найти модуль вектора $bar{a}=(-1 ; 1)$
Решение. Для нахождения модуля вектора, заданного на плоскости воспользуемся формулой:
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}$$
Подставляя в неё координаты заданного вектора, будем иметь:
$$|bar{a}|=sqrt{(-1)^{2}+1^{2}}=sqrt{1+1}=sqrt{2}$$
Ответ. $|bar{a}|=sqrt{2}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В пространстве заданны точки
$A(2 ;-4 ; 1)$ и $B(-2 ; 0 ; 3)$. Найти модуль вектора
$overline{A B}$
Решение. Найдем координаты вектора $overline{A B}$. Для этого из координат конца
(точки $B$ ) вычтем соответствующие координаты начала (точки
$A$ ):
$$overline{A B}=(-2-2 ; 0-(-4) ; 3-1)=(-4 ; 4 ; 2)$$
Далее для нахождения модуля вектора $overline{A B}$ воспользуемся формулой:
$|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}$
Подставляя координаты вектора $overline{A B}$, получим:
$$|overrightarrow{A B}|=sqrt{(-4)^{2}+4^{2}+2^{2}}=sqrt{16+16+4}=sqrt{36}=6$$
Ответ. $|overrightarrow{A B}|=6$
Читать дальше: как найти координаты вектора.
Заказать задачи по любым предметам можно здесь от 10 минут
Модуль вектора
Формула
Чтобы найти модуль вектора по координатам нужно извлечь квадратный корень из суммы квадратов его координат, то есть найти длину вектора.
Если вектор задан на плоскости в виде $ overline{a} = (x;y) $, то вычисляется модуль по формуле: $$ |overline{a}|=sqrt{x^2+y^2} $$
В случае, когда вектор задан в пространстве тремя координатами $ overline{a}= (x;y;z) $, то модуль находится по формуле: $$ |overline{a}|=sqrt{x^2+y^2+z^2} $$
Для нахождения модуля вектора нам понадобится знать:
- Координаты вектора
- Формулы
Примеры решений
| Пример |
| Найти модуль вектора $ overline{a} = (3;4;0) $ |
| Решение |
|
Зная координаты мы первым делом определяем на плоскости или в пространстве задана задача. В нашем случае координат у вектора три, поэтому в пространстве (было бы две координаты, то на плоскости). Используем вторую формулу для пространственной задачи: $$ |overline{a}|=sqrt{x^2+y^2+z^2} $$ Подставляя в формулу в место $ x,y,z $ числа из задания получаем модуль: $$ |overline{a}|=sqrt{3^2+4^2+0^2} = sqrt{9+16+0} = sqrt{25}=5 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ |overline{a}|= sqrt{25}=5 $$ |
© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
10.Разложение вектора по ортам.
Из прямоугольного параллелепипеда
(рис. 4.1) следует:
.
Но
,
,
,
,
Следовательно,
(4.3)
Равенство (4.3) и есть формула разложения
вектора
по ортам координатных осей.
Таким образом, координатная запись
вектора может быть осуществлена двумя
способами:
20.Модуль вектора. Векторявляется диагональю прямоугольного
параллелепипеда (рис. 4.1). Квадрат длины
диагонали равен сумме квадратов трех
его измерений:
,
отсюда следует:
,
и наконец, получаем искомую формулу:
(4.4)
Модуль вектора равен корню квадратному
из суммы квадратов его координат.
4.3. Линейные операции над векторами.
Сформулируем правила действийнад векторами в координатной форме.
.Координаты суммы (разности) векторов
равны суммам (разностям) соответствующих
координат этих векторов.
Пусть
тогда
(4.5)
При умножении вектора на скаляр его
координаты умножаются на этот скаляр.
Если
и
– скалярная величина, то
(4.6)
Покажем применение рассмотренного в
этой главе материала к решению практической
задачи.
Задача 4.1. Даны векторы:
Найти: координаты и модуль вектора
Решение.Используем координатную
запись векторов и правила линейных
операций над ними:
Модуль вектора
вычислим по формуле (4.4):
Ответ.
4.4. Направляющие косинусы вектора
О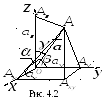
4.2. Направляющими косинусами
ненулевого вектора называются косинусы
углов, которые этот вектор образуют с
осями координат (рис. 4.2).
Выразим координаты вектора
через его модуль и углы
:
С помощью данных равенств найдем
выражения направляющих косинусов через
координаты вектора
и его модуль:
(4.7)
Вычислим сумму квадратов направляющих
косинусов вектора
:
Полученный результат в векторной алгебре
сформулирован в виде следующего
утверждения:
Сумма квадратов направляющих
косинусов ненулевого вектора равна
единице:
(4.8)
Задача 4.2.Определить направляющие
косинусы вектора
а также убедиться в справедливости
тождества(4.8).
Решение.10. Определим координаты
и модуль вектора:
20. Вычислим направляющие косинусы
вектора
30. Проверим справедливость
тождества (4.8):
Ответ.
4.5. Координаты точки в пространстве. Вычисление координат вектора и его модуля по координатам его начала и конца.
В
понятие координат точки в пространстве
через понятие радиус-вектора.
Определение 4.3. Радиус-вектором
точки М называется вектор с началом в начале координат и концом
в точке М, то есть вектор
(рис. 4.3).
В качестве координат точки М примем
координаты радиус-вектора.
Определение 4.4. Координатами
точки в пространстве называются
координаты ее радиус-вектора.
Координаты точки М (рис. 4.3) обозначаются
символом:,
или.
Таким образом,
Поставим задачу:найти координаты
и модуль вектора
,
если известны координаты его начала и
конца:
(рис. 4.4).
Р
и
,
выразим координаты векторачерез координаты векторов
и
(см. определение 4.4), получим:
(4.9)
Координаты вектора равны соответствующим
разностям координат конца и начала
этого вектора.
Задача 4.3.Даны две точки:
Найти координаты, разложение по ортам
координатных осей, модуль и направляющие
косинусы вектора
Решение.Для определения координат
векторавоспользуемся
формулой (4.9):
По формуле (4.4) вычислим модуль вектора
:
Найдем направляющие косинусы вектора
:
Вычислим сумму квадратов направляющих
косинусов:
Ответ.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
31.03.2015657.07 Кб9укр 1.docx
- #
- #
- #
- #
- #
- #
Вектором является направленный отрезок. Длина этого отрезка является длиной вектора.
Длина вектора b⃗vec{b} обозначается ∣b⃗∣.left | vec{b} right |. Модуль числа имеет аналогичное обозначение и длина вектора часто называется модулем вектора.
Длина нулевого вектора равна нулю.
Нахождение длины вектора по его координатам
Длина вектора, который задан своими координатами, – это квадратный корень из суммы квадратов его координат.
Для того чтобы найти длину вектора, заданного своими координатами, нужно извлечь квадратный корень из суммы квадратов его координат.
- Для вектора b⃗=(bx;by),vec{b}=(b_{x};b_{y}), заданного на плоскости, длина вычисляется по формуле ∣b⃗∣left |vec{b} right|=bx2+by2sqrt {b_{x}^{2}+b_{y}^{2}}.
- Для вектора b⃗=(bx;by;bz),vec{b}=(b_{x};b_{y};b_{z}), заданного в пространстве, длина вычисляется по формуле ∣b⃗∣=bx2+by2+bz2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}.
Пример 1
Найти длину вектора b⃗=(6;−4).vec{b}=(6;-4).
Вектор задан на плоскости, поэтому воспользуемся первой формулой: ∣b⃗∣=bx2+by2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}}.
Подставим координаты вектора b⃗vec{b} в формулу, получим: ∣b⃗∣=62+(−4)2=36+16=52=213left | vec{b} right |=sqrt {6^{2}+(-4)^{2}}=sqrt {36+16}=sqrt {52}=2sqrt {13}.
Ответ: 2132sqrt {13}.
Пример 2
Найти длину вектора d⃗=(1;3;5).vec{d}=(1;3;5).
Вектор задан в пространстве, поэтому воспользуемся второй формулой:
∣d⃗∣=dx2+dy2+dz2left | vec{d} right |=sqrt {d_{x}^{2}+d_{y}^{2}+d_{z}^{2}}.
Подставим координаты вектора d⃗vec{d} в формулу, получим:
∣d⃗∣=12+32+52=1+9+25=35left | vec{d} right |=sqrt {1^{2}+3^{2}+5^{2}}=sqrt {1+9+25}=sqrt {35}.
Нахождение длины вектора по координатам точек его начала и конца
Для нахождения длины вектора CD⃗vec{CD}, где C(cx;cy)C(c_{x};c_{y}) и D(dx;dy)D(d_{x};d_{y}) существует определенная последовательность действий:
- Найти координаты вектора CD⃗vec{CD} по формуле: ∣CD⃗∣=(dx−cx;dy−cy)left | vec{CD} right |=(d_{x}-c_{x};d_{y}-c_{y}).
- Найти длину вектора по его координатам по формуле: ∣CD⃗∣=(dx−cx)2+(dy−cy)2left | vec{CD} right |=sqrt {(d_{x}-c_{x})^{2}+(d_{y}-c_{y})^{2}}.
Аналогично находится длина вектора CD⃗,vec{CD}, заданного в пространстве, где C(cx;cy;cz)C(c_{x};c_{y};c_{z}) и D(dx;dy;dz)D(d_{x};d_{y};d_{z}):
- Найти координаты вектора CD⃗vec{CD} по формуле: CD⃗=(dx−cx;dy−cy;dz−cz).vec{CD}=(d_{x}-c_{x};d_{y}-c_{y};d_{z}-c_{z}).
- Найти длину вектора по его координатам по формуле: ∣CD⃗∣=(dx−cx)2+(dy−cy)2+(dz−cz)2left | vec{CD} right |=sqrt {(d_{x}-c_{x})^{2}+(d_{y}-c_{y})^{2}+(d_{z}-c_{z})^{2}}.
Пример 1
На плоскости заданы точки E(−1;3)иK(3;−4)E(-1;3) и K(3;-4). Найти длину вектора EK⃗.vec{EK}.
Найдем координаты вектора EK⃗.vec{EK}. Для этого из координат конца вычтем координаты начала, получим:
EK⃗=(3−(−1);−4−3)=(3+1;−4−3)=(4;−7).vec{EK}=(3-(-1);-4-3)=(3+1;-4-3)=(4;-7).
Воспользуемся формулой ∣b⃗∣=bx2+by2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}} для нахождения длины вектора, получим:
∣EK⃗∣=42+(−7)2left | vec{EK} right |=sqrt {4^{2}+(-7)^{2}}=16+49sqrt {16+49}=65sqrt {65}.
Пример 2
В пространстве заданы точки C(1;2;3)C(1;2;3) и D(3;4;5).D(3;4;5). Найти длину вектора CD⃗.vec{CD}.
Найдем координаты вектора CD⃗.vec{CD}. Для этого из координат конца вычтем координаты начала, получим: CD⃗=(3−1;4−2;5−3)=(2;2;2).vec{CD}=(3-1;4-2;5-3)=(2;2;2).
Воспользуемся формулой ∣b⃗∣=bx2+by2+bz2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}+b_{z}^{2}} для нахождения длины вектора, получим: ∣b⃗∣=22+22+22=4+4+4=12=23left | vec{b} right |=sqrt {2^{2}+2^{2}+2^{2}}=sqrt {4+4+4}=sqrt {12}=2sqrt 3.
Нахождение длины вектора по теореме косинусов
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Для треугольника со сторонами a,b,ca, b, c и углами α,βalpha, beta и γ,gamma, противолежащими этим сторонам соответственно, справедливы равенства:
b=a2+c2−2a⋅c⋅cos(β),b=a^{2}+c^{2}-2acdot ccdot cos (beta), a=b2+c2−2b⋅c⋅cos(α),a=b^{2}+c^{2}-2bcdot ccdot cos (alpha), c=a2+b2−2a⋅b⋅cos(γ).c=a^{2}+b^{2}-2acdot bcdot cos (gamma).
Аналогично поступают и с векторами. Рассмотрим пример.
Пример 1
Длины векторов KL⃗vec{KL} и KM⃗vec{KM} равны соответственно 2 и 4, а угол между ними равен π4.frac{pi }{4}. Вычислите длину вектора LM⃗.vec{LM}.
Длина вектора LM⃗vec{LM} равна длине стороны LMLM в треугольнике LMKLMK. Также нам известны стороны KLKL и KMKM треугольника LMKLMK. Они равны длинам соответствующих векторов. Нам известен угол между векторами. Найдем сторону LMLM треугольника △KLM.triangle KLM.
LM2=KL2+KM2−2KL⋅KM⋅cos∠LKM.LM^2=KL^2+KM^2-2KLcdot KMcdot cos angle LKM.
LM2=22+42−2⋅2⋅4⋅cosπ4=4+16−82=20−82.LM^2=2^2+4^2-2cdot 2cdot4cdot cos frac{pi }{4}=4+16-8sqrt{2}=20-8sqrt{2}.
LM=20−82.LM=sqrt{20-8sqrt{2}}.
∣LM⃗∣=20−82.|vec{LM}|=sqrt{20-8sqrt{2}}.
