Путь
Пусть частица, двигаясь вдоль некоторой траектории, переместилась из точки 1 в точку 2.
Путь s (или s) равен измеренному вдоль траектории расстоянию, пройденному частицей в процессе движения (длина траектории).
Путь является величиной скалярной, неотрицательной

Связь между путем и модулем скорости частицы
Пусть за малый промежуток времени t частица переместилась из точки 1 в точку 2 траектории. Пройденный частицей путь обозначим s.
Если уменьшать промежуток времени t, точка 2 траектории будет приближаться к точке 1. При этом различие между длиной дуги s и стягивающей ее хордой – модулем перемещения | r| будет уменьшаться.
32

Связь между путем и модулем скорости частицы
В пределе при t 0 отношение длины дуги s к длине хорды | r| равно единице:
lim s 1
t 0 r
Тогда
v dr lim r lim s ds dt t t dtt 0 t 0
Следовательно, модуль вектора скорости равен производной пути по времени

Связь между путем и модулем скорости частицы
Зная зависимость модуля скорости v от времени, можно вычислить пройденный частицей путь:
v dsdt , ds v(t)dt
Интегрируя это равенство, получим:
|
s |
t2 |
t2 |
|
ds v(t)dt, |
s v(t)dt |
|
|
0 |
t1 |
t1 |
34

Графическое определение пути
Если задана графическая зависимость модуля скорости частицы от времени t, то путь s, пройденный частицей за промежуток времени от t1 до t2 численно равен площади криволинейной трапеции, ограниченной графиком функции v(t), осью t и вертикальными прямыми t = t1 и t = t2.
t2
s v(t)dt
t1 35

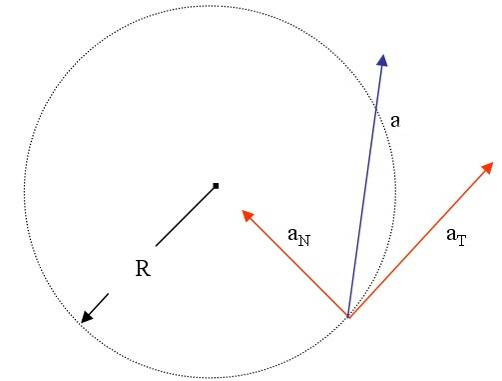
Полное ускорение частицы
Полное ускорение частицы a можно представить в виде суммы двух перпендикулярных друг другу составляющих:
aa an
Модуль полного ускорения:
|
dv 2 |
v4 |
||||||
|
2 |
2 |
||||||
|
a a |
an |
||||||
|
R2 |
|||||||
|
dt |
36

Полное ускорение частицы
37
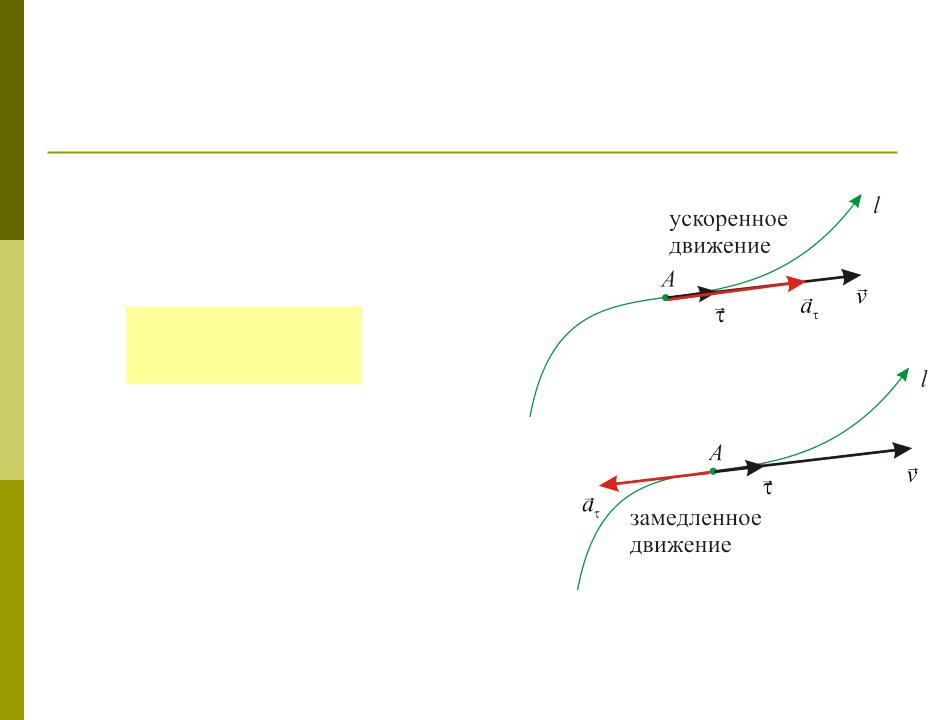
Тангенциальное (касательное) ускорение
Первое слагаемое в этом выражении называется
тангенциальным (касательным) ускорением:
|
dv |
d 2s |
|||||
|
a |
||||||
|
2 |
||||||
|
dt |
dt |
|||||
Вектор a направлен по касательной
к траектории движения частицы; при этом a v, если движение
ускоренное; a v, если движение замедленное.
Тангенциальное ускорение частицы характеризует изменение скорости частицы по модулю (если a = 0,
|
движение является равномерным). |
38 |
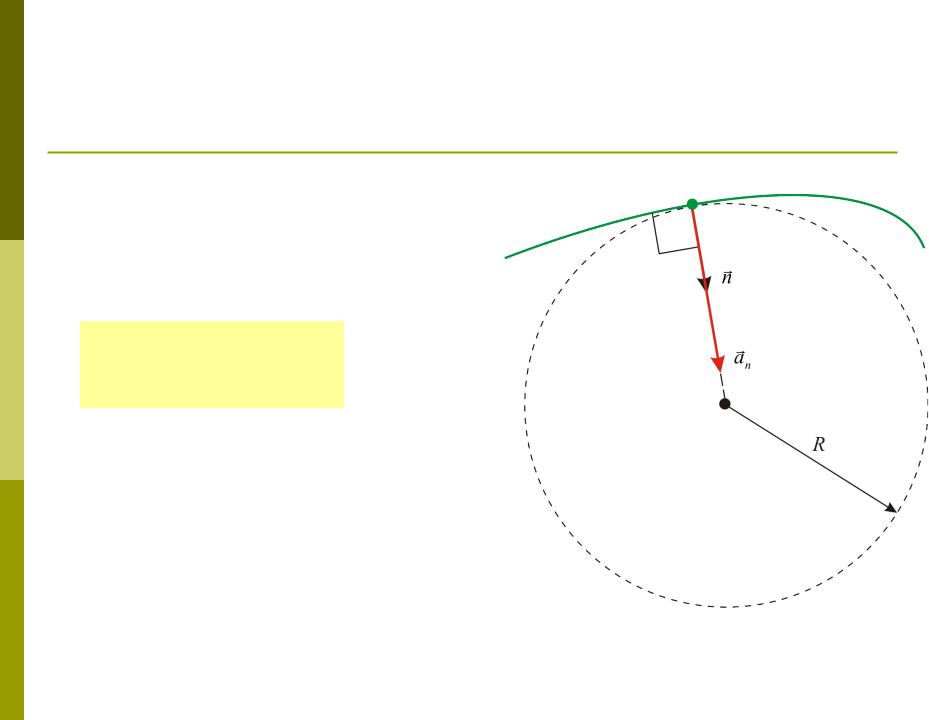
Нормальное
(центростремительное)
ускорениеВторое слагаемое называется
нормальным
(центростремительным) ускорением:
|
v2 |
1 ds |
2 |
||||
|
an |
R |
n |
n |
|||
|
R dt |
Вектор an всегда перпендикулярен касательной к тракетории движения, т.е. an v и an a .
Нормальное ускорение характеризует изменение скорости по направлению (для прямолинейного движения, когда R

ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
1.4 Твердое тело в механике. Виды движения твердого тела
40
Соседние файлы в папке МЕХАН
- #
- #
- #
- #
- #
Пусть в однородном магнитном поле, индукция которого , движется частица со скоростью
, направленной перпендикулярно линиям индукции. Масса частицы m и заряд q. Так как сила Лоренца
перпендикулярна скорости
движения частицы (см. рис. 170), то эта сила изменяет только направление скорости, сообщая частице центростремительное ускорение, модуль которого согласно второму закону Ньютона:
В результате частица движется по окружности, радиус которой можно определить из формулы :
Период Т обращения частицы, движущейся по окружности в однородном магнитном поле:
(30.2)
Как следует из выражения (30.2), период обращения частицы не зависит от модуля скорости её движения и радиуса траектории, а определяется только модулем заряда частицы, её массой и значением индукции магнитного поля.
От теории к практике
В однородном магнитном поле, модуль индукции которого В = 4,0 мТл, перпендикулярно линиям индукции поля движется электрон. Чему равен модуль ускорения электрона, если модуль скорости его движения ? Масса и модуль заряда электрона mе = 9,1 · 10–31 кг и е = 1,6 · 10–19 Кл соответственно.
Подобное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Движущиеся с огромными скоростями заряженные частицы из космоса захватываются магнитным полем Земли и образуют так называемые радиационные пояса (рис. 170.2), в которых частицы перемещаются по винтообразным траекториям между северным и южным магнитными полюсами туда и обратно за промежуток времени порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния (рис. 170.3).
Если заряженная частица в момент возникновения внешнего электрического поля покоилась, то , где U — напряжение между точками, в которых находилась частица в моменты возникновения внешнего электрического поля и выхода из него, q — модуль заряда частицы. Поэтому модуль скорости частицы при выходе из электрического поля:
Если после этого частица попадает в однородное магнитное поле, индукция которого перпендикулярна направлению её скорости, то радиус окружности, по дуге которой будет двигаться частица,
, откуда
Величину называют удельным зарядом частицы. Поэтому если опытным путём определить радиус траектории движения частицы в магнитном поле, то, зная индукцию магнитного поля и ускоряющее напряжение электрического поля, можно рассчитать удельный заряд частицы. Этот метод используют при конструировании приборов, которые называют масс–спектрометрами.
Интересно знать
Поскольку сила Лоренца направлена под углом 90° к скорости движения заряженной частицы в каждой точке траектории (рис. 171), то работа этой силы при движении заряженной частицы в магнитном поле равна нулю. Поэтому кинетическая энергия частицы, движущейся в стационарном (не изменяющемся во времени) магнитном поле, не изменяется, т. е. стационарное магнитное поле нельзя использовать для ускорения заряженных частиц.
Увеличение кинетической энергии частицы, т. е. её разгон, возможно под действием электрического поля (в этом случае изменение кинетической энергии частицы равно работе силы поля). Поэтому в современных ускорителях (рис. 172) заряженных частиц электрическое поле используют для ускорения, а магнитное — для «формирования» траектории движения заряженных частиц.
1. Как определить модуль силы, действующей со стороны магнитного поля на движущуюся в нём заряженную частицу?
2. Как определяют направление силы Лоренца?
3. Заряженная частица движется в однородном магнитном поле со скоростью, направленной перпендикулярно линиям индукции. По какой траектории движется частица?
4. От чего зависит период обращения заряженной частицы в однородном магнитном поле?
5. Почему сила Лоренца изменяет направление скорости движения частицы, но не влияет на её модуль?
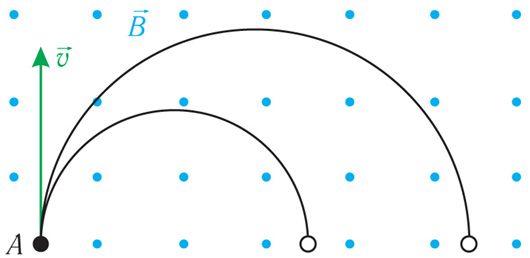
6. На рисунке 172.1 представлены траектории движения двух частиц, имеющих одинаковые заряды. Частицы влетают в однородное магнитное поле из одной точки А с одинаковыми скоростями. Определите знак заряда частиц. Объясните причину несовпадения траекторий их движения.
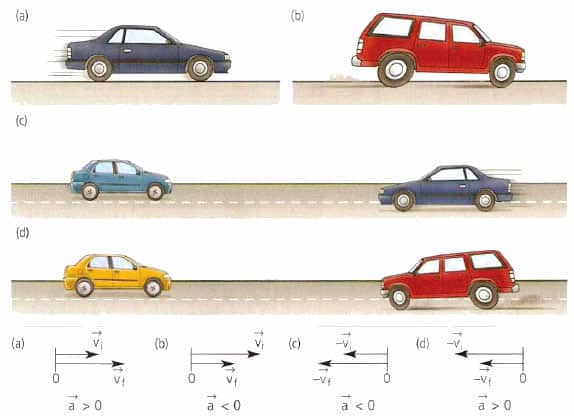
В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.
Что такое ускорение?
Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение — это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:
a = dv/dt.
Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:
a = (v2 — v1)/(t2 — t1).
Где v2 и v1 — скорости в моменты времени t2 и t1 соответственно.
Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.
Движение по прямой и ускорение
Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:
v = v0±a*t;
l = v0*t±a*t2/2.
Здесь v0 — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:
±a = (v — v0)/t;
±a = 2*(l — v0*t)/t2.
Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).
Полное ускорение и его компоненты при движении тела по кривой
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:
a = √(at2 + an2).
Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:
an = v2/r.
Здесь r — радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.
Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.
Угловое ускорение
Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:
α = dω/dt.
Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.
Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:
α = at/r.
Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.
Пример решения задачи
Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:
v = 2 + 3*t2 + 2*t3.
Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.
Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:
at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.
Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).
Нормальная компонента вычисляется так:
an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.
Теперь можно рассчитать полное ускорение. Оно будет равно:
a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.
То есть, полное ускорение практически полностью образовано нормальной компонентой.
Наконец, ускорение угловое определяется по формуле:
α = at/r = 76/0,2 = 380 рад/с2.
Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.