Найти модуль и направление напряженности
поля в центре кольца радиуса а, по
которому однородно распределен зарядq>0, а в кольце
сделана прорезь ширинойb
<< a.
Решение.
Рассмотрим кольцо без прорези. Тогда в
силу симметрии в центре кольца поле
равно нулю. С другой стороны это поле
является суперпозицией поля кольца с
прорезью
и поле заряда в прорези
(рис.):
,
откуда
|
|
Поле
,
в силу малости прорези, описывается
полем точечного заряда величинойqb=qb/(2πa—b)qb/2πa,
имеет величину
и направлено от прорези. Поэтому
и направлено от центра кольца к
прорези.
Пример 1.7
Тонкое проволочное кольцо радиуса
мм имеет однородно распределенный заряд
мк Кл. Каково будет приращение силы,
растягивающей проволоку, если в центре
кольца поместить точечный зарядмк Кл?
Решение.
Выберем на кольце элементарную дугу
с зарядом
.
По закону Кулона сила взаимодействия
зарядови
равна
,
где(
— линейная плотность заряда).
|
|
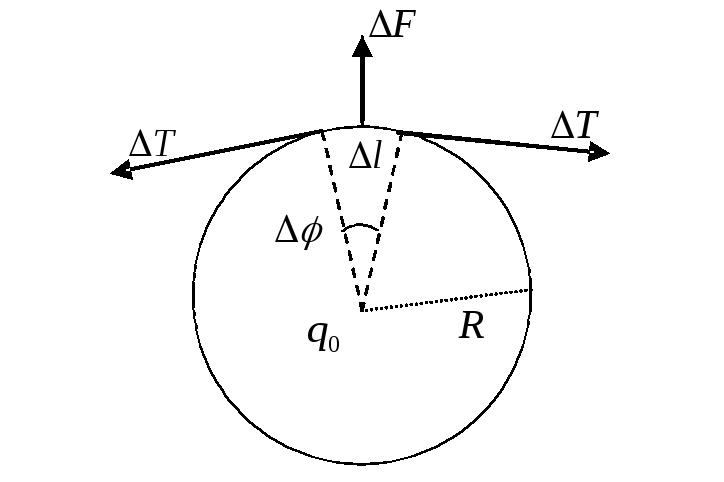
В равновесии величина силы
равна равнодействующей приращения сил,
растягивающих проволоку.
Из подобия треугольников (см. рисунок)
имеем:
где
.
Выражая
,получим:
.
Пример 1.8
Кольцо радиуса
из тонкой проволоки имеет однородно
распределенный заряд.
Найдите модуль напряженности электрического
поля на оси кольца как функцию расстояниядо его центра. Исследуйте
при
.
Решение.
Разобьем заряд кольца на бесконечно
малые элементы с зарядами
,
которые можно рассматривать как точечные.
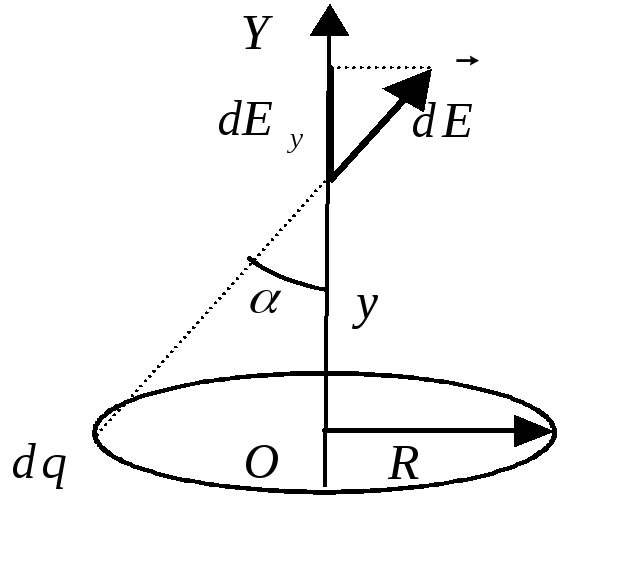
На оси кольца выберем произвольную
точку с координатой.
Заряд
создаст в этой точке напряженность поля
,
направление которого показано на
рисунке, а его величина равна:
.
Напряженность результирующего поля
найдем, воспользовавшись принципом
суперпозиции. В силу симметрии
результирующее поле будет направлено
вдоль оси
(см. рисунок). Поэтому
,
где:
|
|
Учитывая, что
,
получим:
.
Суммируя вклады всех элементов кольца,
найдем для проекции результирующего
поля:
.
Рассмотрим напряженность поля на больших
расстояниях
.
,
т.е. на больших расстояниях система
ведет себя как точечный заряд.
График
представлен
на рисунке.
Точки, в которых напряженность поля
принимает максимальные значения, имеют
координаты.
Пример 1.9
Находящийся в вакууме тонкий прямой
стержень длины
заряжен однородно зарядом
.Найдите модуль напряженности электрического
поля как функцию расстоянияr
от цента стержня до точки прямой,
совпадающей с осью стержня.
Исследуйте полученное выражение при
.
Решение.
Выделим на стержне элементарный заряд
,
находящийся на участке стержня,
на расстоянииот начала
координатной оси
.
В произвольной точке на оси стержня с
координатойзаряд
создает напряженность поля
величиной:
|
|
Применяя принцип суперпозиции для
нахождения напряженности поля,
создаваемого стержнем в искомой точке,
получим:
График напряженности поля, создаваемого
заряженным стержнем на его оси представлен
на рисунке.
|
|
При
напряженность
поля
,
т.е. на больших расстояниях поле стержня
ведет себя как поле точечного зарядаq,помещенного в
центр стержня.
Пример 1.10
Тонкий прямой стержень заряжен с линейной
плотностью
,
гдедлина стержня,
расстояние от конца стержня,
положительная постоянная. Найдите
модуль напряженности электрического
поля при.
Решение.
Разобьем заряженный стержень на
бесконечно малые элементы
с зарядами
|
|
Каждый заряд
создает в точке
напряженность поля
:
Все вектора
сонаправлены. Поэтому для нахождения
напряженности поля,
создаваемого всем заряженным стержнем
в точке,
применим принцип суперпозиции, суммируя
величины элементарных векторов:
Соседние файлы в папке Примеры решений
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2018-05-14
Тонкое непроводящее кольцо радиуса $R$ заряжено с линейной плотностью $lambda = lambda_{0} cos phi$, где $lambda_{0}$ — постоянная, $phi$ — азимутальный угол. Найти модуль вектора напряженности электрического поля:
а) в центре кольца;
б) на оси кольца в зависимости от расстояния $x$ до его центра. Исследовать полученное выражение при $x gg R$.
Решение:
(a) Данное распределение заряда показано на рис. Симметрия этого распределения означает, что вектор $vec{E}$ в точке О направлен вправо, а его величина равна сумме проекции на направление $vec{E}$ векторов $d vec{E}$ от элементарных зарядов $dq$. Проекция вектора $d vec{E}$ на вектор $vec{E}$ равна
$dE cos phi = frac{1}{4 pi epsilon_{0} } frac{dq}{R^{2} } cos phi$,
где $dq = lambda Rd phi = lambda_{0} R cos phi d phi$.
Интегрируя (1) по $phi$ между 0 и $2 pi$, найдем величину вектора $E$:
$E = frac{ lambda_{0} }{4 pi epsilon_{0}R } int_{0}^{ 2 pi} cos^{2} phi d phi = frac{ lambda_{0} }{4 epsilon_{0} R }$.
Следует отметить, что этот интеграл решается самым простым способом, если учесть, что $langle cos^{2} phi rangle = 1/2$. затем
$int_{0}^{ 2 pi} cos^{2} phi d phi = langle cos^{2} phi rangle 2 pi = pi$.
(б) Возьмем элемент $S$ с азимутальным углом $phi$ от оси х, причем элемент, находиться в центре под углом $d phi$.
Элементарное поле в точке P от элемента
$frac{ lambda_{0} cos phi d phi R }{4 pi epsilon_{0} (x^{2} + R^{2} ) }$ вдоль SP с компонентами
$frac{ lambda_{0} cos phi d phi R }{4 pi epsilon_{0} (x^{2} + R^{2} ) } times { cos theta вдоль OP, sin theta вдоль OS }$
где $cos theta = frac{x}{ sqrt{x^{2} + R^{2} } }$
Компонента вдоль OP исчезает при интегрировании $int_{0}^{ 2 pi} cos phi d phi = 0$
Компонент вдль OS может быть разбит на части вдоль OX и OY с помощью
$frac{ lambda_{0} R^{2} cos phi d phi }{4 pi epsilon_{0} (x^{2} + R^{2} )^{1/2} } times { cos theta вдоль OX, sin theta вдоль OY }$
Интегрируя, компонента вдоль оси OY исчезает.
Окончательно
$E = E_{x} = frac{ lambda_{0}R^{2} }{4 epsilon_{0} (x^{2} + R^{2} )^{3/2} }$
Для $x gg R$
$E_{x} = frac{p}{ 4 pi epsilon_{0} x^{3} }$ где $p = lambda_{0} pi R^{2}$
Как определить напряженность электрического поля в центре кольца?
Чему равна напряженность
электрического поля в центре тонкого кольца радиусом 0,1 м, по которому
равномерно распределен заряд 20 мкКл?
Решение.
Разобьем кольцо на
малые участки с зарядами Dq, которые можно считать точечными. Каждому элементу Dq найдется диаметрально расположенный элемент, и геометрическая
сумма напряженностей электрических полей этих двух симметричных элементов в
центре кольца, будет равна 0. Поэтому напряженность электрического поля в
центре кольца равна 0.
Ответ: Напряженность
электрического поля в центре кольца будет равна 0.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.
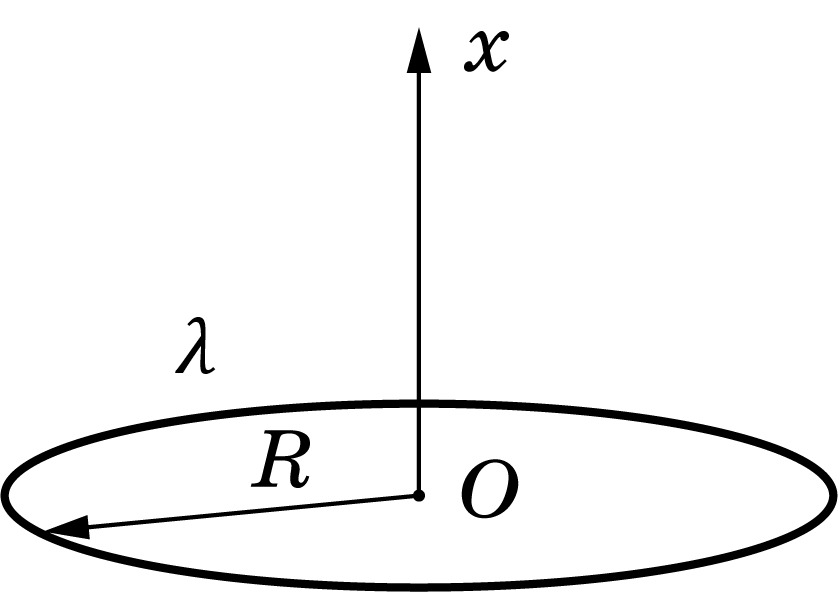
Часть A. Кольцо (2.0 балл)
Кольцо радиуса $R$ равномерно заряжено по периметру с линейной плотностью заряда $lambda$.
A1
0.20
Найдите напряженность поля в центре заряженного кольца.
A2
0.30
Найдите потенциал на оси кольца на расстоянии $x$ от его центра.
A3
0.30
Найдите модуль напряженности поле на оси кольца на расстоянии $x$ от его центра.
A4
0.60
При каком значении $x$ напряженность поля на оси кольца максимальна? Найдите эту максимальную напряженность.
A5
0.60
Найдите напряженность поля, создаваемого диском радиуса $R$, равномерно заряженного по поверхности с плотностью заряда $sigma$ на его оси на расстоянии $x$ от центра.
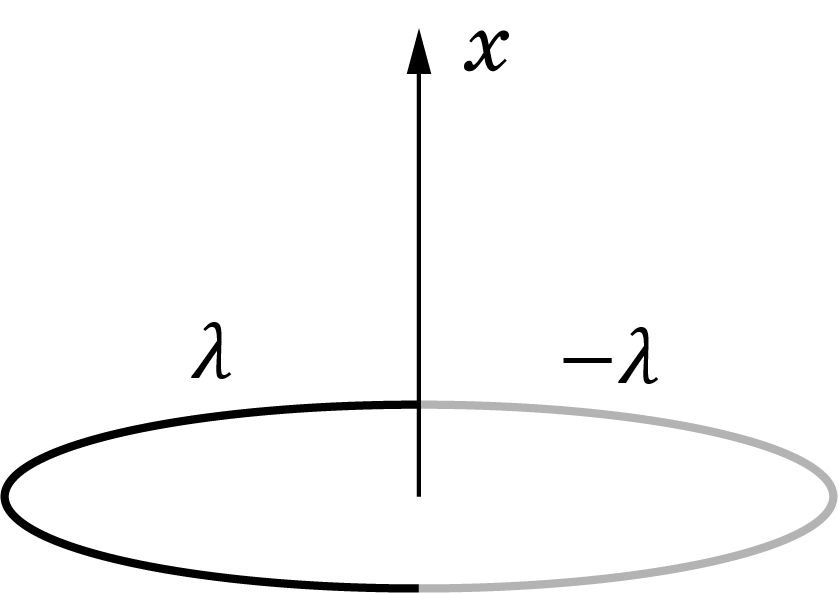
Часть B. Две половины кольца (2.0 балла)
Кольцо состоит из двух половин радиуса $R$, одна из которых равномерно заряжена с линейной плотностью заряда $lambda$, а другая — с $-lambda$.
B1
0.20
Найдите потенциал на оси кольца на расстоянии $x$ от его центра.
B2
1.00
Найдите модуль напряженности поля в центре кольца.
B3
0.80
Найдите модуль напряженности поля на оси кольца на расстоянии $x$ от его центра.
Часть C. Цилиндр (6 баллов)
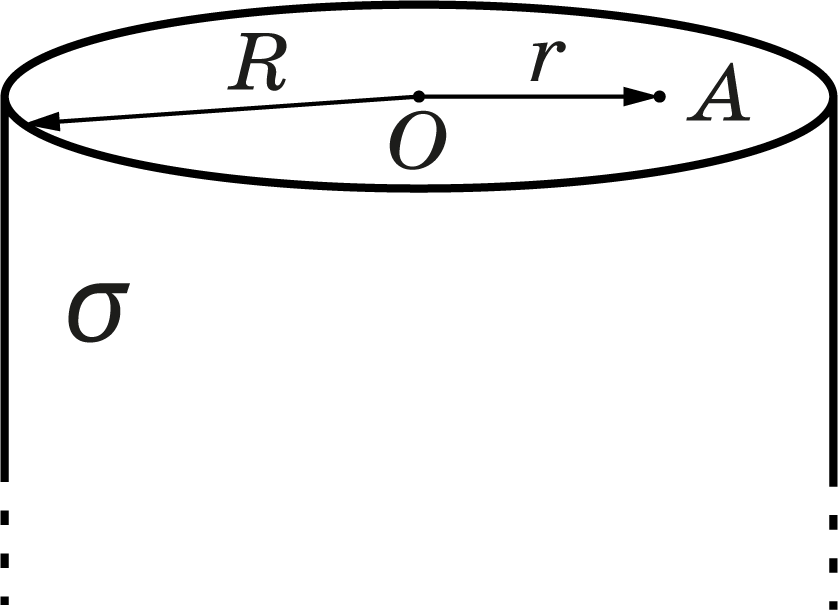
Бесконечный цилиндр радиуса $R$ равномерно заряжен по боковой поверхности с поверхностной плотностью заряда $sigma$.
C1
0.30
Чему равен модуль напряженности электрического поля на расстоянии $r < R$ от оси цилиндра?
Теперь рассмотрим полубесконечный цилиндр того же радиуса $R$, равномерно заряженного с той же поверхностной плотностью заряда $sigma$. От вас потребуется найти поле в каждой точке основания цилиндра (см. рис.).
C2
2.00
Найдите модуль напряженности поля в центре основания цилиндра $O$.
C3
0.70
Рассмотрим точку $A$ в основании цилиндра, находящуюся на расстоянии $r < R$ от точки $O$. Найдите проекцию вектора напряженности электрического поля на линию $OA$.
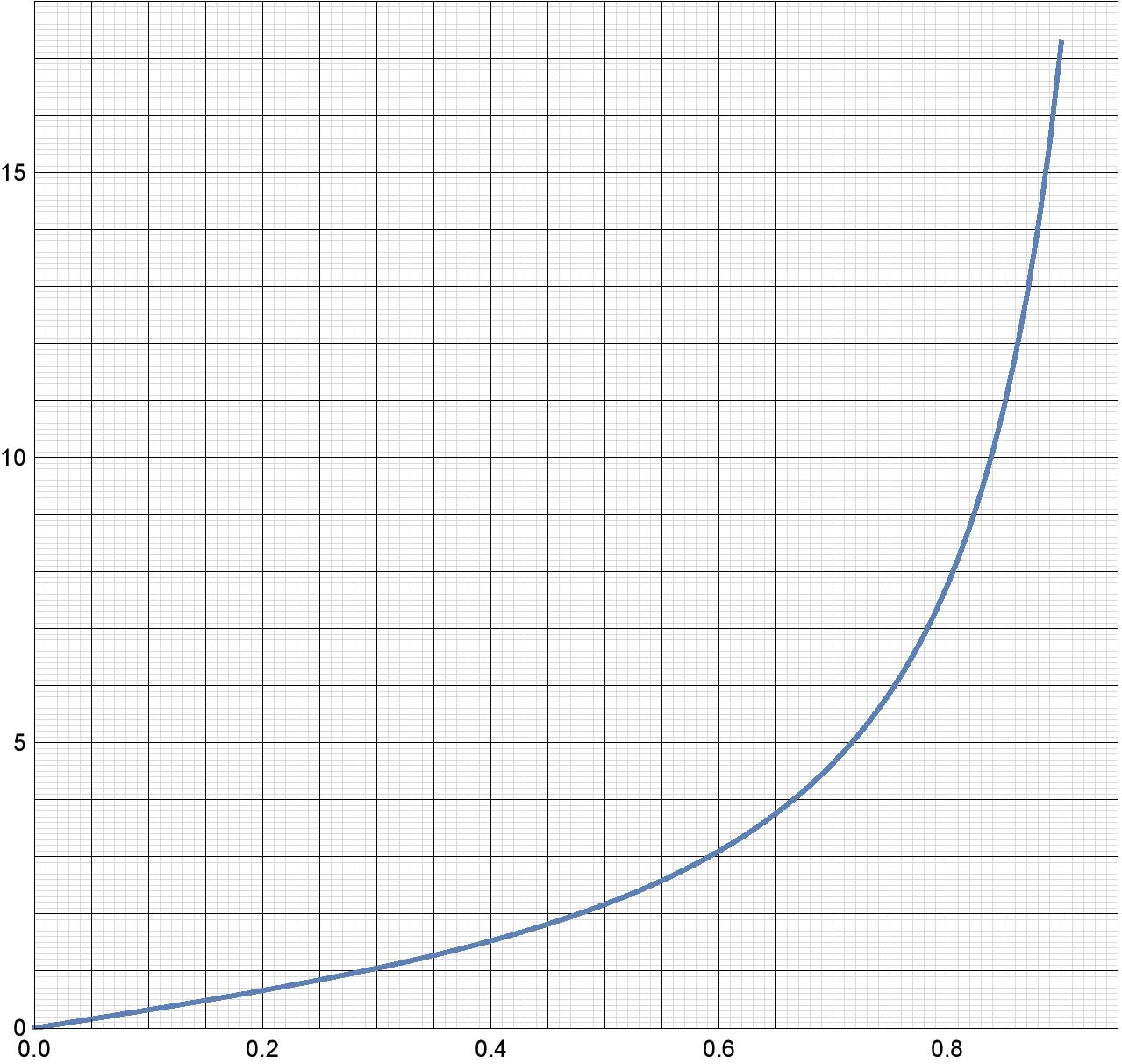
Для решения следующего пункта вам может понадобиться зависимость радиальной компоненты напряженности поля кольца в его плоскости. Если кольцо радиуса $R$ равномерно заряжено зарядом $Q$, то на расстоянии $r$ от его центра радиальная компонента напряженности поля равна
$$E_r=frac{kQ}{2{pi}R^2}cdot y(x)$$
где $x=r/R$. График зависимости $y(x)$ представлен на рисунке ниже.
C4
3.00
Для рассматриваемого полубесконечного цилиндра найдите модуль напряженности электрического поля в точке $A$, находящейся на расстоянии $r=0,!9R$ от точки $O$.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5