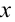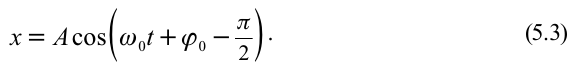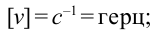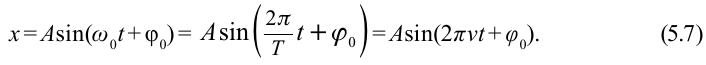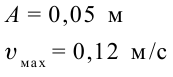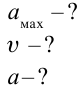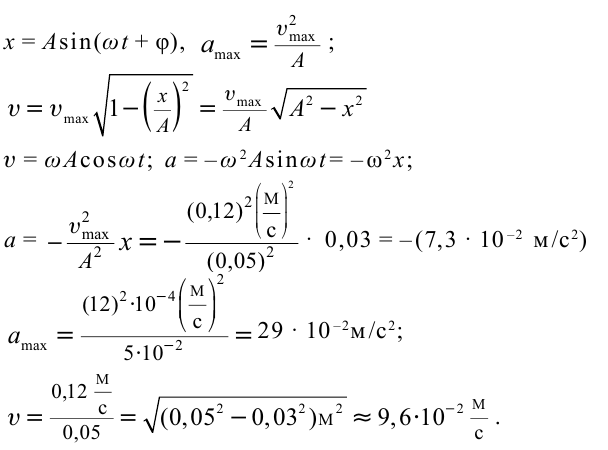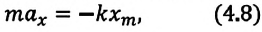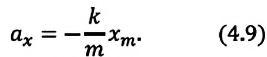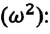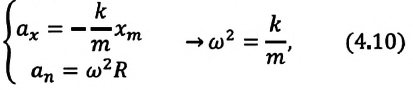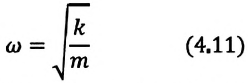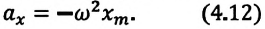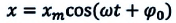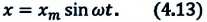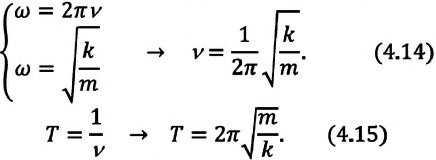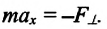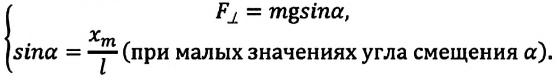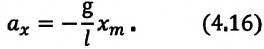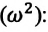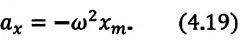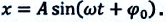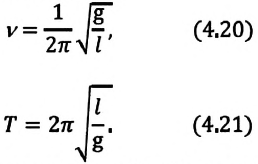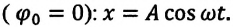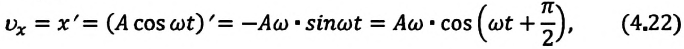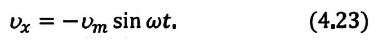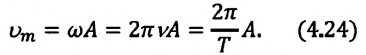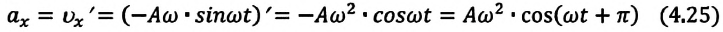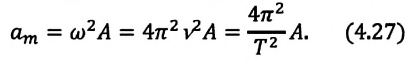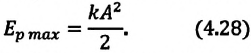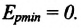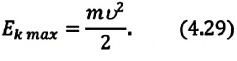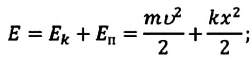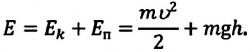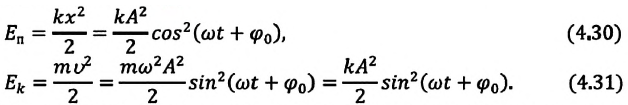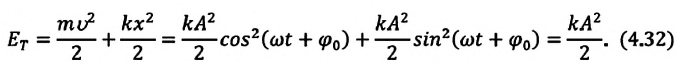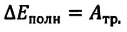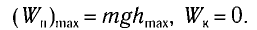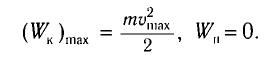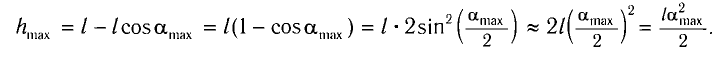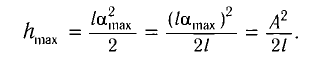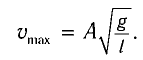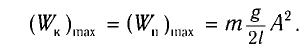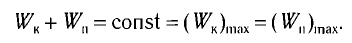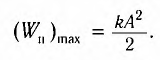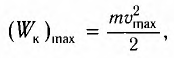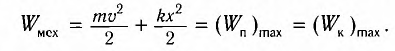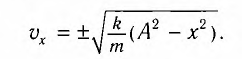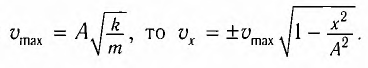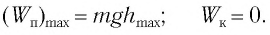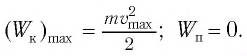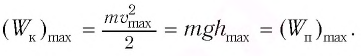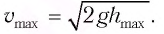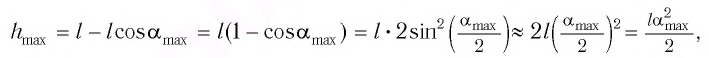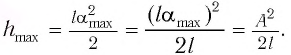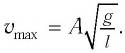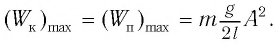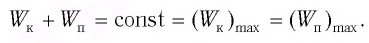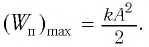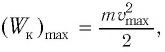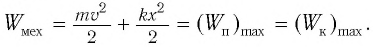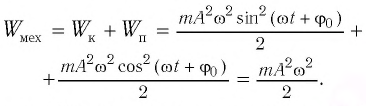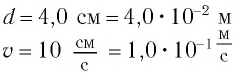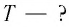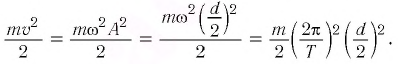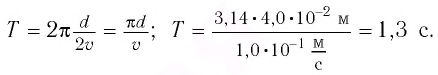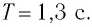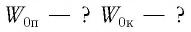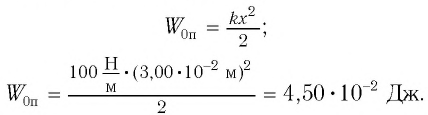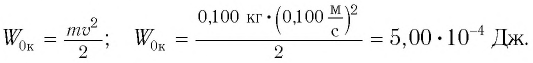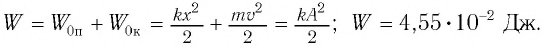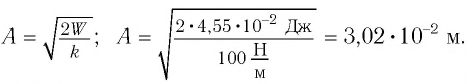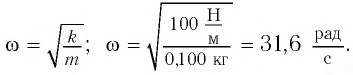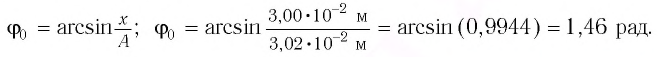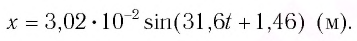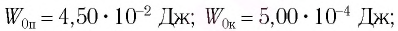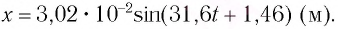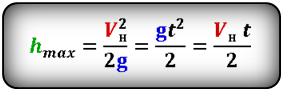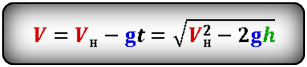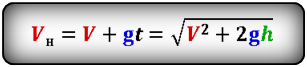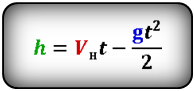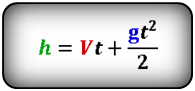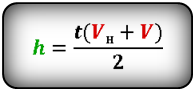Скорость тела характеризуется направлением и модулем. Иными словами, модуль скорости – это число, которое показывает, насколько стремительно тело передвигается в пространстве. Перемещение полагает метаморфоза координат.
Инструкция
1. Введите систему координат, касательно которой вы будете определять направление и модуль скорости . Если в задаче теснее задана формула зависимости скорости от времени, вводить систему координат не надобно – предполагается, что она теснее есть.
2. По имеющейся функции зависимости скорости от времени дозволено обнаружить значение скорости в всякий момент времени t. Пускай, скажем, v=2t?+5t-3. Если требуется обнаружить модуль скорости в момент времени t=1, примитивно подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.
3. Когда задача требует обнаружить скорость в исходный момент времени, подставьте в функцию t=0. Таким же образом дозволено обнаружить время, подставив вестимую скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t?+5t-3=0. Отсель t=[-5±?(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а от того что время не может быть негативным, остается только t=1/2.
4. Изредка в задачах уравнение скорости дается в завуалированной форме. Скажем, в условии сказано, что тело двигалось равноускоренно с негативным убыстрением -2 м/с?, а в первоначальный момент скорость тела составляла 10 м/с. Негативное убыстрение обозначает, что тело равномерно замедлялось. Из этих условий дозволено составить уравнение для скорости : v=10-2t. С всей секундой скорость будет уменьшаться на 2 м/с, пока тело не остановится. В конце пути скорость обнулится, следственно легко обнаружить всеобщее время движения: 10-2t=0, откуда t=5 секунд. Через 5 секунд позже начала движения тело остановится.
5. Помимо откровенного движения тела, существует еще и движение тела по окружности. В всеобщем случае оно является криволинейным. Тут появляется центростремительное убыстрение, которое связано с линейной скоростью формулой a(c)=v?/R, где R – радиус. Комфортно рассматривать также угловую скорость ?, причем v=?R.
Модуль числа n представляет собой число единичных отрезков от начала координат до точки n. Причем не главно, в какую сторону будет отсчитываться это расстояние – вправо либо налево от нуля.
Инструкция
1. Модуль числа также принято называть безусловной величиной этого числа . Он обозначается короткими вертикальными линиями, проведенными слева и справа от числа . Скажем, модуль числа 15 записывается дальнейшим образом: |15|.
2. Помните, что модуль может быть только позитивным числом либо нулем. Модуль позитивного числа равен самому числу. Модуль нуля равен нулю. То есть для всякого числа n, которое огромнее либо равно нулю, будет объективна дальнейшая формула |n| = n. Скажем, |15| = 15, то есть модуль числа 15 равен 15-ти.
3. Модулем негативного числа будет то же число, но с противоположным знаком. То есть для всякого числа n, которое поменьше нуля, будет объективна формула |n| = -n. Скажем, |-28| = 28. Модуль числа -28 равен 28-ми.
4. Дозволено находить модули не только для целых, но и для дробных чисел. Причем в отношении дробных чисел действуют те же правила. Скажем, |0,25| = 25, то есть модуль числа 0,25 будет равен 0,25. А |-?| = ?, то есть модуль числа -? будет равен ?.
5. При работе с модулями пригодно знать, что модули противоположных чисел неизменно равны друг другу, то есть |n| =|-n|. Это является основным свойством модулей. Скажем, |10| = |-10|. Модуль числа 10 равен 10-ти, верно так же, как модуль числа -10. Помимо того, |a – b| = |b – a|, потому что расстояние от точки a до точки b и расстояние от b до a равны друг другу. Скажем, |25 – 5| = |5 – 25|, то есть |20| = |- 20|.
Для нахождения метаморфозы скорости определитесь с типом движения тела. В случае если движение тела равномерно, изменение скорости равно нулю. Если тело движется с убыстрением, то изменение его скорости в весь момент времени дозволено узнать, если отнять от мгновенной скорости в данный момент времени его исходную скорость.
Вам понадобится
- секундомер, спидометр, радар, рулетка, акселерометр.
Инструкция
1. Определение метаморфозы скорости произвольно движущегося по прямой траекторииС поддержкой спидометра либо радара измерьте скорость тела в начале и конце отрезка пути. После этого от финального итога отнимите первоначальный, это и будет изменение скорости тела.
2. Определение метаморфозы скорости тела, движущегося с ускорениемНайдите убыстрение тела. Используйте акселерометр либо динамометр. Если знаменита масса тела, тогда силу, действующую на тело, поделите на его массу (a=F/m). Позже этого измерьте время, за которое происходил процесс метаморфозы скорости . Дабы обнаружить изменение скорости , умножьте значение убыстрения на время, за которое происходило это изменение (?v=a•t). Если убыстрение измерить в метрах на секунду в квадрате, а время – в секундах, то скорость получится в метрах на секунду. Если нет вероятности замерить время, но вестимо, что скорость менялась на определенном отрезке пути, спидометром либо радаром, измерьте скорость в начале этого отрезка, после этого с поддержкой рулетки либо дальномера измерьте длину этого пути и убыстрение. Любым из вышеописанных способов измерьте убыстрение, которое действовало на тело. Позже этого обнаружьте финальную скорость тела в конце участка пути. Для этого возведите исходную скорость в квадрат, прибавьте к ней произведение длины участка на убыстрение и число 2. Из итога извлеките квадратный корень. Дабы обнаружить изменение скорости , от полученного итога отнимите значение исходной скорости .
3. Определение метаморфозы скорости тела при поворотеЕсли изменилась не только величина, но и направление скорости , то обнаружьте ее изменение через векторную разность исходной и финальной скорости . Для этого измерьте угол между векторами. После этого от суммы квадратов скоростей отнимите удвоенное их произведение, умноженное на косинус угла между ними: v1?+v2?-2v1v2•Cos(?). Из полученного числа извлеките квадратный корень.
Видео по теме
Для определения скорости разных видов движения потребуются различные формулы. Дабы определить скорость равномерного движения, расстояние поделите на время его прохождения. Среднюю скорость движения находите сложением всех отрезков, которое прошло тело, на всеобщее время движения. При равноускоренном движении узнайте убыстрение, с которым двигалось тело, а при свободном падении высоту, с которой оно предисловие движение.
Вам понадобится
- дальномер, секундомер, акселерометр.
Инструкция
1. Скорость равномерного движения и средняя скоростьИзмерьте расстояние с поддержкой дальномера, которое прошло тело, а время, за которое оно его одолело, с поддержкой секундомера. Позже этого поделите расстояние, пройденное телом на время его прохождения, итогом будет скорость равномерного движения (v=S/t). Если тело движется неравномерно, произведите те же измерения и примените ту же формулу – тогда получите среднюю скорость тела. Это значит, что если бы тело по данному отрезку пути двигалось с полученной скоростью, оно было бы в пути время, равное измеренному. Если тело движется по окружности, измерьте ее радиус и время прохождения полного цикла, после этого радиус умножьте на 6,28 и поделите на время (v=6,28•R/t). Во всех случаях итог получится в метрах в секунду. Для перевода в километры в час помножьте его на 3,6.
2. Скорость равноускоренного движенияИзмерьте убыстрение тела с поддержкой акселерометра либо динамометра, если знаменита масса тела. Секундомером замерьте время движения тела и его исходную скорость, если тело не начинает двигаться из состояния покоя. Если же тело двигается из состояния покоя, она равна нулю. Позже этого узнайте скорость тела, прибавив к исходной скорости произведение убыстрения на время (v=v0+at).
3. Скорость вольно падающего телаС поддержкой дальномера измерьте высоту, с которой падает тело в метрах. Дабы узнать скорость, с которой оно долетит до поверхности Земли (без контроля сопротивления воздуха), умножьте высоту на 2 и на число 9,81 (убыстрение свободного падения). Из итога извлеките квадратный корень. Дабы обнаружить скорость тела на всякий высоте, применяйте ту же методологию, только от исходной высоты, отнимайте нынешнюю и полученное значение подставляйте взамен высоты.
Видео по теме
Человек привык воспринимать представление “скорость ” как что-то больше примитивное, чем это есть на самом деле. Подлинно, проносящийся на перекрестке автомобиль движется с определенной скорость ю, в то время как человек стоит и отслеживает за ним. Но если человек находится в движении, то умнее говорить не об безусловной скорости, а об относительной ее величине. Обнаружить относительную скорость дюже легко.
Инструкция
1. Дозволено продолжить рассмотрение темы движущегося на перекрестка на автомобиле. Человек же, стоя на красном свете светофора, стоит и глядит на проезжающий автомобиль. Человек статичен, следственно примем его за систему отсчета. Система отсчета – такая система, касательно которой движется какое-нибудь тело либо другая физическая точка.
2. Возможен, автомобиль движется со скорость ю 50 км/ч. Но, возможен, что человек побежал следом автомобилю (дозволено, скажем, взамен автомобиля представить маршрутку либо проезжающий мимо автобус). Скорость бега человека 12 км/ч. Таким образом, скорость данного механического транспортного средства представится человеку не столь и стремительной, как было прежде, когда он стоял! В этом каждая и суть относительной скорости. Относительная скорость неизменно измеряется касательно подвижной системы отсчета. Таким образом, скорость автомобиля не будет для пешехода 50 км/ч, а 50 – 12 = 38 км/ч.
3. Дозволено разглядеть еще один живой пример. Довольно припомнить всякий из моментов, когда человек, сидя у окна автобуса, отслеживает за проносящимися мимо автомобилями. Подлинно, из окна автобуса их скорость кажется примитивно потрясающей. И это не изумительно, чай, если принять автобус за систему отсчета, то скорость автомобиля и скорость автобуса надобно будет сложить. Возможен, что автобус движется со скорость ю 50 км/ч, а машины 60 км/ч. Тогда 50 + 60 = 110 км/ч. Именно с такой скорость ю эти самые автомобили проносятся мимо автобуса и пассажиров в нем.Эта же скорость будет объективна и действительна и в том случае, если за систему отсчета принять всякий из проезжающих мимо автобусов автомобилей.
Кинематика постигает разные виды движения тела с заданной скоростью, направлением и траекторией. Дабы определить его расположение касательно точки начала пути, надобно обнаружить перемещение тела .
Инструкция
1. Движение тела происходит по некоторой траектории. В случае откровенного движения ею является прямая линия, следственно обнаружить перемещение тела достаточно примитивно: оно равно пройденному пути. В отвратном случае определить его дозволено по координатам исходного и финального расположения в пространстве.
2. Величина перемещения физической точки является векторной, от того что она имеет направление. Следственно, дабы обнаружить ее числовое значение, нужно вычислить модуль вектора, соединяющего точки начала пути и его окончания.
3. Разглядим двухмерное координатное пространство. Пускай тело проделало путь от точки A (x0, y0) до точки B (x, y). Тогда, дабы обнаружить длину вектора АВ, опустите проекции его концов на оси абсцисс и ординат. Геометрически проекции касательно той и иной координатной оси дозволено представить в виде катетов прямоугольного треугольника с длинами:Sx = x – x0;Sy = y – y0, где Sx и Sy – проекции вектора на соответствующих осях.
4. Модуль вектора, т.е. длина перемещения тела , в свою очередь, является гипотенузой этого треугольника, длину которой легко определить по теореме Пифагора. Он равен квадратному корню из суммы квадратов проекций:S = ?(Sx? + Sy?).
5. В трехмерном пространстве:S = ?(Sx? + Sy? + Sz?), где Sz = z – z0.
6. Это формула является всеобщей для всякий разновидности движения. Вектор перемещения владеет несколькими свойствами: • его модуль не может превышать длину пройденного пути;• проекция перемещения может быть как позитивной, так и негативной величиной, в то время как величина пути неизменно огромнее нуля;• в всеобщем случае перемещение не совпадает с траекторией движения тела , а его модуль не равен пути.
7. В частном случае откровенного движения тело перемещается только по одной оси, скажем, оси абсцисс. Тогда длина перемещения равна разности финальной и исходной первой координаты точек:S = x – x0.
От модуля исходной скорости во многом зависят колляции движения тела. Для того дабы обнаружить эту величину, нужно воспользоваться дополнительными измерениями либо данными. Величина модуля исходной скорости может являться основополагающей колляцией, скажем, для огнестрельного оружия.
Вам понадобится
- – рулетка;
- – дальномер;
- – секундомер;
- – акселерометр;
- – спидометр;
- – угломер;
- – хронограф.
Инструкция
1. Вначале определитесь с типом движения. Если оно равномерное, то довольно измерить длину пути, по которому переместилось тело, сделав это рулеткой, дальномером либо иным доступным методом, и поделить это значение на время, за которое это перемещение осуществлялось. От того что движение равномерное, то модуль скорости на протяжении каждого пути будет идентичен, так что полученная скорость будет равна исходной.
2. При равноускоренном откровенном движении измерьте при помощи акселерометра убыстрение тела, а с подмогой секундомера время его движения, спидометром финальную скорость в конце отрезка пути. Обнаружьте значение модуля исходной скорости, отняв от финальной скорости произведение убыстрения на время движения v0=v-a*t. Если незнакомо значение убыстрения, измеряйте расстояние, которое покрыло тело за время t. Сделайте это при помощи рулетки либо дальномера.
3. Зафиксируйте значение финальной скорости. Обнаружьте исходную скорость, отняв от удвоенного значения расстояния S, поделенного на время, значение финальной скорости v, v0=2S/t-v. Когда значение финальной скорости измерить трудно, а убыстрение знаменито, воспользуйтесь иной формулой. Для этого измеряйте перемещение тела, а также время, которое оно было в пути. От значения перемещения отнимите произведение убыстрения на квадрат времени, поделенное на 2, а итог поделите на время, v0=(S-at?/2)/t либо v0=S/t-at/2.
4. Когда тело начинает движение под углом к горизонту, на него воздействует сила тяжести. Для того дабы обнаружить модуль исходной скорости, при помощи угломера замеряйте угол к горизонту, под которым тело начинает двигаться. При помощи рулетки либо дальномера замеряйте расстояние, на котором тело упадет на поверхность земли. Дабы определить модуль исходной скорости, расстояние S поделите на синус удвоенного угла ?. Из полученного итога извлеките квадратный корень, v0=?(S/sin(2?)).
5. Дабы измерить модуль исходной скорости пули, выпущенной из стрелкового оружия, используйте хронограф. Для этого установите его так, как указано в его инструкции, от того что хронографы бывают различных типов. Позже этого сделайте выстрел из оружия, на табло хронографа появится итог. Выстрелите еще несколько раз и возьмите среднее значение показаний хронографа. Это и будет модуль исходной скорости пули, выпущенного из данного типа стрелкового оружия.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора — вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами — единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? «Наверное какой-то жуткий», подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки — это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора — это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему «механика твердых тел». А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.
Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.
Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости. Все точки камня движутся по окружностям. Во время опыта хорошо видно, что отрывающиеся раскаленные частички-опилки уходят по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек вращающегося точильного камня.
Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.
Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.
Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.
Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис. 1.54. Возьмем приращение длины пути 



направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.
Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения
Здесь 
Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение 

Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения. Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.
Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.
Как найти максимальную скорость
Задачи физики и математики часто требуют найти максимальную скорость объекта на протяжении всего пути. Данный вид задач относится к разделу кинематики. Рассмотрим алгоритм нахождения максимальной скорости.

Инструкция
Запишите уравнение зависимости скорости от времени.
Найдите производную правой части уравнения и приравняйте её к нулю. Найдите момент времени t, в который производная равна нулю. Если функция периодическая, достаточно рассмотреть какой-либо один период.
Из полученных значений t выберите точки максимума функции. Точка максимума — это минус.
Посчитайте значение функции скорости в точках максимума. Выберите наибольшее.
Если задан конкретный промежуток времени, сравните значения функции скорости на граничных точках и в точках максимума. Выберите наибольшее из них.
Видео по теме
Полезный совет
Функцию зависимости скорости от времени можно получить, дифференцируя функцию пройденного пути, либо интегрируя функцию ускорения. Во втором случае понадобятся еще начальные условия.
Источники:
- как находится максимальная скорость
Содержание:
Гармонические колебания:
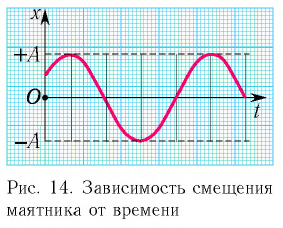
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
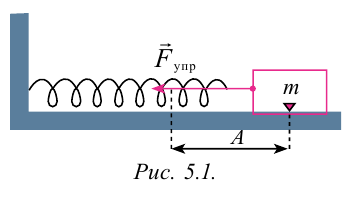
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 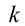
Если груз, который находится в равновесии, потянем вправо на расстояние 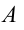
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
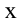
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 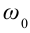
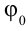
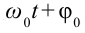
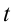
Из математики известно, что 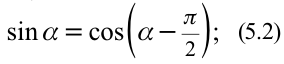
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 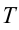

б) частота колебания 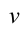
Единица
c) циклическая частота 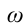
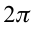
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
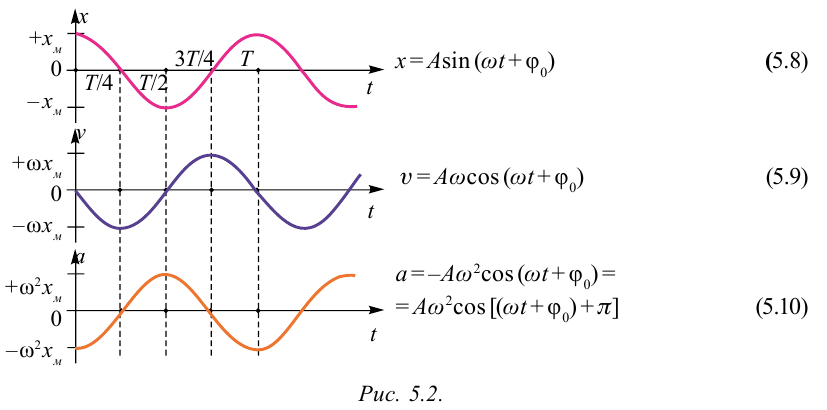
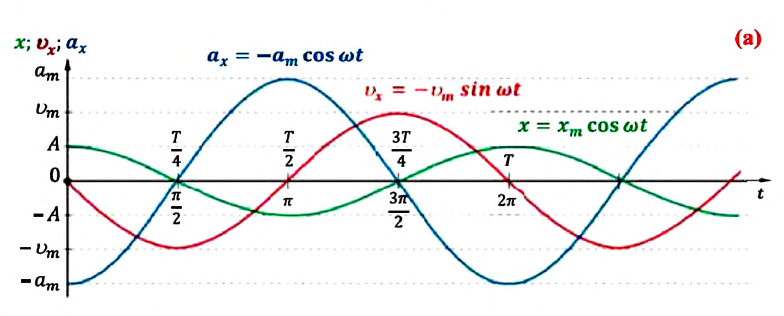
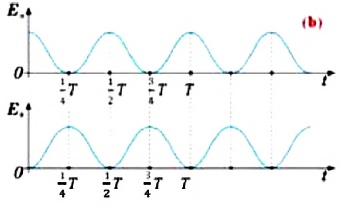
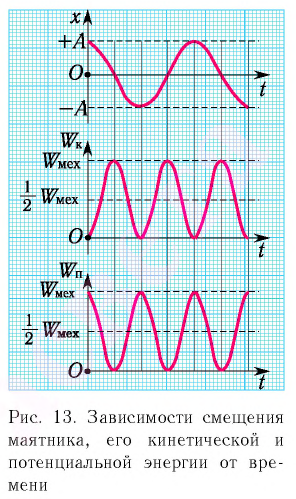
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
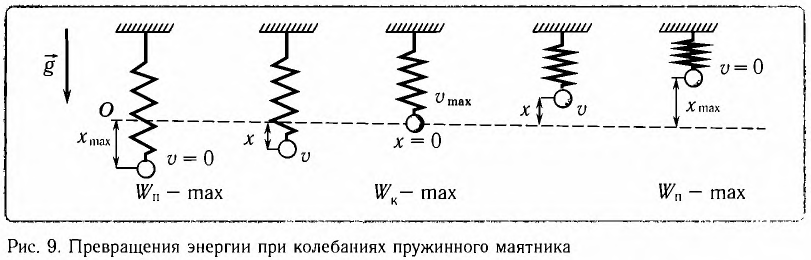
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
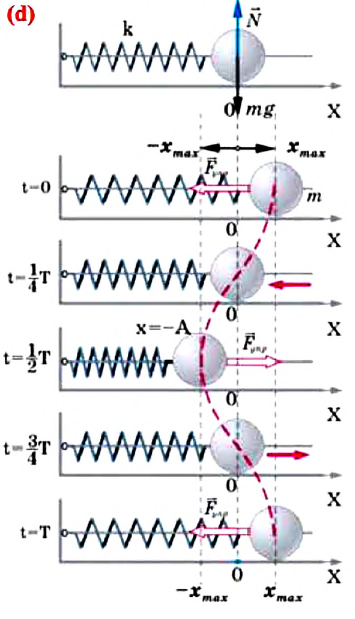
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 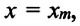
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 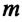
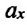
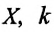
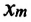
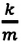
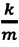
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 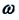
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 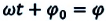
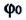
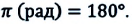
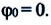

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
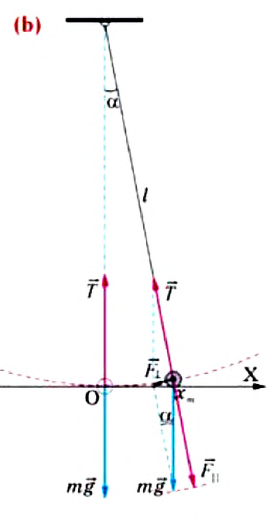
Сила тяжести 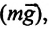
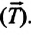
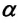
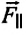
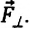
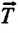
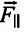
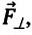
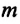
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 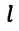
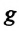
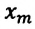
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 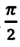
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 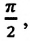
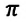
Превращения энергии при гармонических колебаниях
Теоретический материал
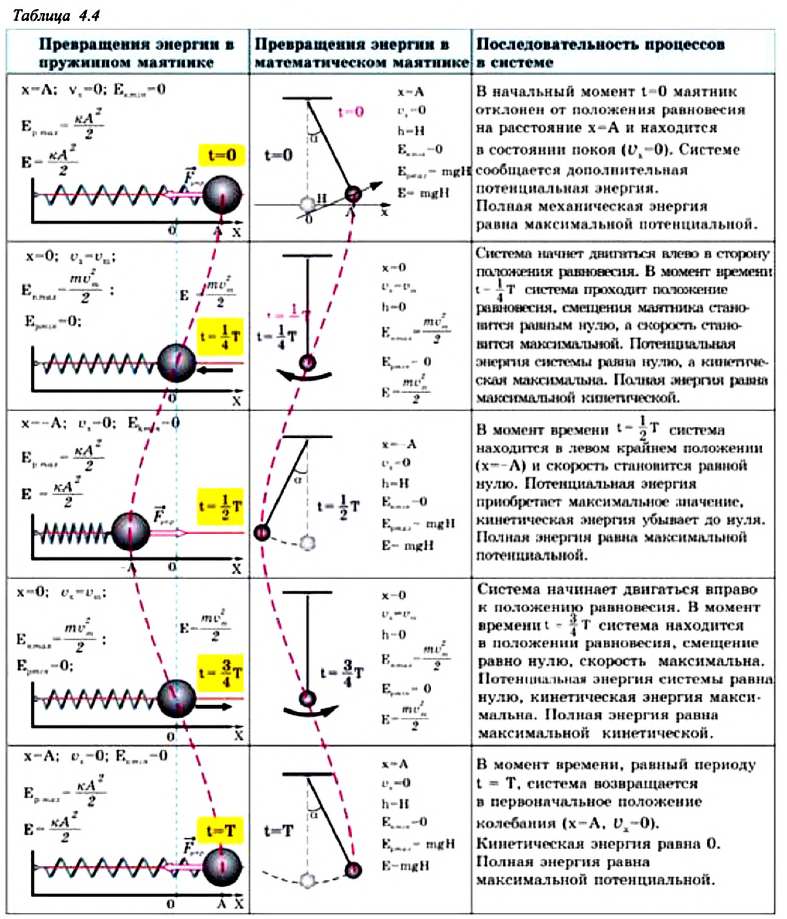
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 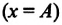
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 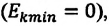
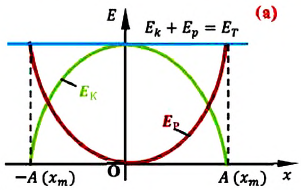
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 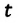
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
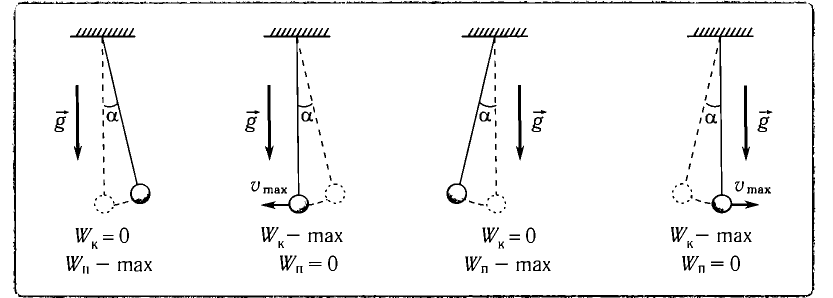
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
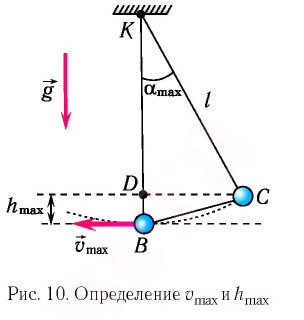
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
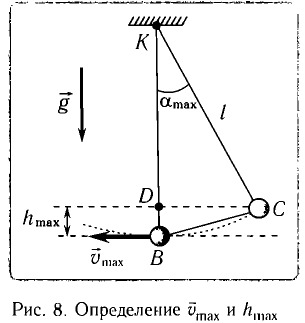
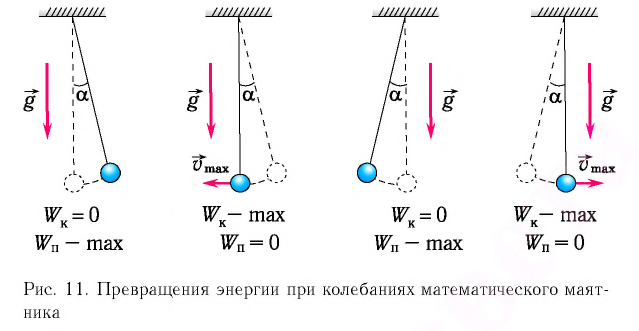
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
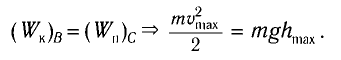
Отсюда найдем модуль максимальной скорости маятника:
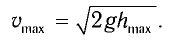
Высоту 
Если колебания малые, то 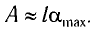
Отсюда
Подставив выражение для 
Подставляя выражения для 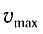

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 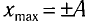
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 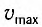
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 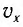
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 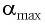
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 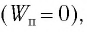
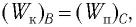
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 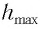
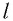
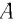
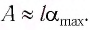
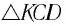
или
Подставив выражение (3) для 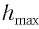
Подставляя выражения (3) для 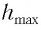
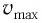
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
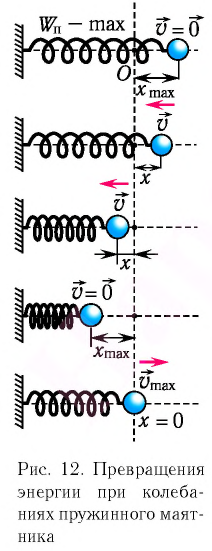
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 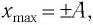
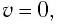
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 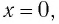
где 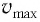
В положениях между крайними точками полная энергия
С учетом выражений для координаты 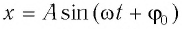
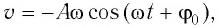
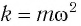
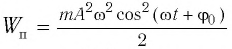
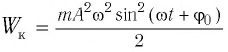
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 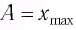
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 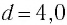
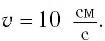
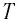
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 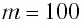
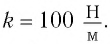
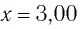
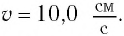
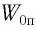
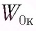
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
В начальный момент времени 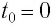
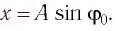
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
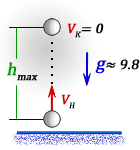
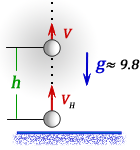
1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
h max
— максимальная высота достигнутая телом за время t
Vк — конечная скорость тела на пике, равная нулю
Vн — начальная скорость тела
t — время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула максимальной высоты (h max):
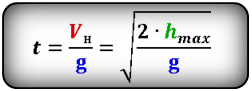
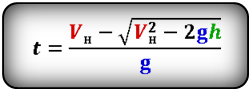
Формула времени за которое тело достигло максимальную высоту (t):
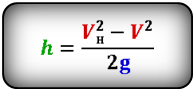
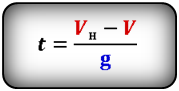
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h — расстояние пройденное телом за время t
Vн — начальная скорость тела
V — скорость тела в момент времени t
t — время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула скорости тела в момент времени t (V):
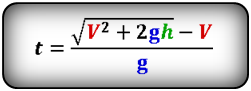
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
На чтение 4 мин Просмотров 3к. Опубликовано 25.11.2021
Содержание
- Ответ или решение 2
- Скорость движения рассчитывается по формуле
- Найдем уравнение скорости
- Ответ
- Уравнение скорости
- График скорости
- Некоторые частные случаи
- Заключение
Ответ или решение 2
Скорость движения рассчитывается по формуле
- Скорость движения равна производной формулы пути;
- чтобы найти максимальную скорость, нужно найти производную скорости;
- затем нужно определить точки максимума;
- подставить их в уравнение скорости.
Нам дано уравнение пути s = -10t 3 + 15t 2 + 2t
Найдем уравнение скорости
S` = — 10 * 3t 2 + 15 * 2t + 2 = — 30t 2 + 30t + 2
v = — 30t 2 + 30t + 2
Найдем точки максимума этой функции
Для этого найдем производную этой функции.
v`= — 30 * 2t + 30 = — 60t + 30
Приравняем ее к нулю.
Переносим 30 в правую часть, меняя знак.
Делим все уравнение на (- 30).
Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.
Берем любую точку, например, 0.
— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)
Берем например, точку 1.
— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)
Значит, t = 1/2 — это точка максимума.
Подставим это значение в уравнение скорости.
v = — 30t 2 + 30t + 2
v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.
Ответ: максимальная скорость движения равна 9,5.
Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.
- Попроси больше объяснений
- Следить
- Отметить нарушение
Vazgen1312 05.07.2019
Ответ
Ответ:
Объяснение:
Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)
1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²
S = 0 + 15*1/2 = 7,5 м
2. S = V*t = 15*3 = 45 м
3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.
Еще раз о том, что такое равноускоренное движение
Автомобиль за каждую секунду увеличивает свою скорость на 
На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на 

Уравнение скорости
Воспользовавшись уравнением, определяющим ускорение 
Уравнение скорости в проекциях имеет вид:
Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.
К вопросу о направлении скорости и ускорения
В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.
Рассмотрим наиболее типичные примеры направления скорости и ускорения.
1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).
Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой
В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.
2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).
Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой
Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.
3. Скорость и ускорение взаимно перпендикулярны (рис. 3).
Рис. 3. Скорость и ускорение взаимно перпендикулярны
Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.
Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.
График скорости
График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.
Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения
Проанализируем различные графики.
Первый. Уравнение проекции скорости:
Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:
График начинается в точке
Где
Рис. 5. График функции
Это уравнение прямой, что подтверждается графиками, рассмотренными нами.
Некоторые частные случаи
Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, 
Запись этого уравнения 
Рис. 6. Различные случаи равноускоренного движения
Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси
Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси 
График зависимости ускорения от времени
Равноускоренное движение – это движение, при котором ускорение тела не меняется.
Рис. 7. График зависимости проекций ускорения от времени
Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.
Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:
Произведение ускорения и времени –это изменение скорости за данное время.
Рис. 8. Изменение скорости
Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.
Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.
Заключение
На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.
- Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.narod.ru» (Источник)
- Интернет-портал «youtube.com» (Источник)
- Интернет-портал «fizmat.by» (Источник)
- Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)
1. Что такое равноускоренное движение?
2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:
3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при 
«>