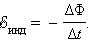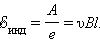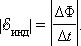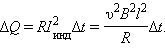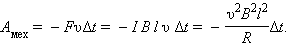Как найти модуль изменения магнитного потока - Avtoru.top

На чтение 13 мин. Опубликовано 12.12.2019

Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока , пронизывающего контур.

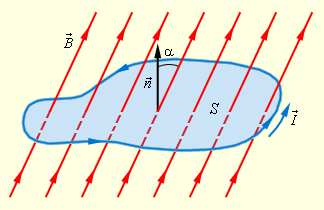
Магнитным потоком Φ через площадь контура называют величину

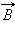
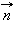
где – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура (рис. 1.20.1).

Рисунок 1.20.1.

Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный , создается магнитным полем с индукцией , пронизывающим по направлению нормали плоский контур площадью :

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции , равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Эта формула носит название закона Фарадея .

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца .

Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.

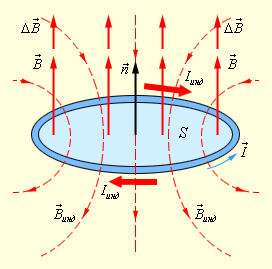Рисунок 1.20.2.

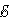
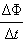
Правило Ленца отражает тот экспериментальный факт, что и всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

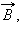
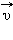
Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длиной скользит со скоростью по двум другим сторонам (рис. 1.20.3).

Рисунок 1.20.3.

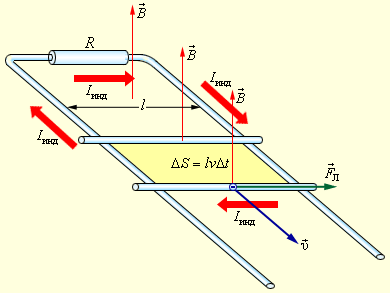
На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью 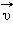зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен

Работа силы _Л на пути равна

По определению ЭДС

В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для 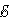можно придать привычный вид. За время Δ площадь контура изменяется на Δ = υΔ. Изменение магнитного потока за это время равно ΔΦ = υΔ. Следовательно,

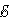
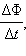
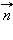
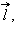
Для того, чтобы установить знак в формуле, связывающей _инд и нужно выбрать согласованные между собой по правилу правого буравчика направление нормали и положительное направление обхода контура как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.

Если сопротивление всей цепи равно , то по ней будет протекать индукционный ток, равный _инд = 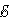_инд/. За время Δ на сопротивлении выделится джоулево тепло

Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера 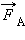. Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен _A = . Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δ эта работа равна

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение . Полная работа силы Лоренца равна нулю . Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным . Его называют вихревым электрическим полем . Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 г.

Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково , но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

В однородном магнитном поле с индукцией 40 мТл находится плоский контур в виде кольца радиусом 5 см, изготовленный из тонкой проволоки. Сначала контур располагается так, что линии индукции магнитного поля перпендикулярны плоскости кольца. Затем кольцо поворачивают вокруг его диаметра на угол 120°. Найдите модуль изменения потока вектора магнитной индукции через кольцо при таком повороте. Ответ выразите в мкВб и округлите до целого числа.

Магнитный поток через рамку равен произведению площади рамки на величину вектора магнитной индукции и на косинус угла между перпендикуляром к рамке и направлением поля:

Найдём модуль изменения потока вектора магнитной индукции:

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

источник – переменное магнитное поле;
обнаруживается по действию на заряд;
не является потенциальным;
линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

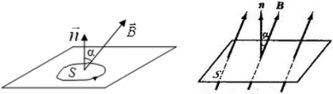
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ) , площади поверхности ( S ) , пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ( alpha ) магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ( N ) витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :

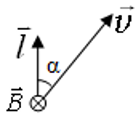
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec ) ЭДС электромагнитной индукции равна:

где ( alpha ) – угол между векторами ( vec ) и ( vec ) .

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

определить направление линий магнитной индукции внешнего магнитного поля;
выяснить, как изменяется магнитный поток;
определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ( varepsilon_ ) , возникающая в катушке с индуктивностью ( L ) , по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ) , создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

закона электромагнитной индукции;
ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

Источник

Самоиндукция

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: самоиндукция, индуктивность, энергия магнитного поля.

Самоиндукция является частным случаем электромагнитной индукции. Оказывается, что электрический ток в контуре, меняющийся со временем, определённым образом воздействует сам на себя.

Ситуация 1 .Предположим, что сила тока в контуре возрастает. Пусть ток течёт против часовой стрелки; тогда магнитное поле этого тока направлено вверх и увеличивается (рис. 1).

Рис. 1. Вихревое поле препятствует увеличению тока

Таким образом, наш контур оказывается в переменном магнитном поле своего собственного тока. Магнитное поле в данном случае возрастает (вместе с током) и потому порождает вихревое электрическое поле, линии которого направлены по часовой стрелке в соответствии с правилом Ленца.

Как видим, вихревое электрическое поле направлено против тока, препятствуя его возрастанию; оно как бы «тормозит» ток. Поэтому при замыкании любой цепи ток устанавливается не мгновенно — требуется некоторое время, чтобы преодолеть тормозящее действие возникающего вихревого электрического поля.

Ситуация 2 . Предположим теперь, что сила тока в контуре уменьшается. Магнитное поле тока также убывает и порождает вихревое электрическое поле, направленное против часовой стрелки (рис. 2).

Рис. 2. Вихревое поле поддерживает убывающий ток

Теперь вихревое электрическое поле направлено в ту же сторону, что и ток; оно поддерживает ток, препятствуя его убыванию.

Как мы знаем, работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура — это ЭДС индукции. Поэтому мы можем дать такое определение.

Явление самоиндукции состоит в том, что при изменении силы тока в контуре возникает ЭДС индукции в этом же самом контуре.

При возрастании силы тока (в ситуации 1) вихревое электрическое поле совершает отрицательную работу, тормозя свободные заряды. Стало быть, ЭДС индукции в этом случае отрицательна.

При убывании силы тока (в ситуации 2) вихревое электрическое поле совершает положительную работу, «подталкивая» свободные заряды и препятствуя убыванию тока. ЭДС индукции в этом случае также положительна (нетрудно убедиться в том, что знак ЭДС индукции, определённый таким образом, согласуется с правилом выбора знака для ЭДС индукции, сформулированным в листке «Электромагнитная индукция»).

Индуктивность

Мы знаем, что магнитный поток, пронизывающий контур, пропорционален индукции магнитного поля: . Кроме того, опыт показывает, что величина индукции магнитного поля контура с током пропорциональна силе тока: B sim I . Стало быть, магнитный поток через поверхность контура, создаваемый магнитным полем тока в этом самом контуре, пропорционален силе тока: .

Коэффициент пропорциональности обозначается и называется индуктивностью контура:

(1)

Индуктивность зависит от геометрических свойств контура (формы и размеров), а также от магнитных свойств среды, в которую помещён контур (Улавливаете аналогию? Ёмкость конденсатора зависит от его геометрических характеристик, а также от диэлектрической проницаемости среды между обкладками конденсатора). Единицей измерения индуктивности служит генри (Гн).

Допустим, что форма контура, его размеры и магнитные свойства среды остаются постоянными (например, наш контур — это катушка, в которую не вводится сердечник); изменение магнитного потока через контур вызвано только изменением силы тока. Тогда , и закон Фарадея приобретает вид:

$mathcal E_i = -L frac{displaystyle Delta I}{displaystyle Delta t vphantom{1^a}} = -LI.$ (2)

Благодаря знаку «минус» в (2) ЭДС индукции оказывается отрицательной при возрастании тока и положительной при убывании тока, что мы и видели выше.

Рассмотрим два опыта, демонстрирующих явление самоиндукции при замыкании и размыкании цепи.

Рис. 3. Самоиндукция при замыкании цепи

В первом опыте к батарейке подключены параллельно две лампочки, причём вторая — последовательно с катушкой достаточно большой индуктивности (рис. 3).

Ключ вначале разомкнут.

При замыкании ключа лампочка 1 загорается сразу, а лампочка 2 — постепенно. Дело в том, что в катушке возникает ЭДС индукции, препятствующая возрастанию тока. Поэтому максимальное значение тока во второй лампочке устанавливается лишь спустя некоторое заметное время после вспыхивания первой лампочки.

Это время запаздывания тем больше, чем больше индуктивность катушки. Объяснение простое: ведь тогда больше будет напряжённость вихревого электрического поля, возникающего в катушке, и потому батарейке придётся совершить большую работу по преодолению вихревого поля, тормозящего заряженные частицы.

Во втором опыте к батарейке подключены параллельно катушка и лампочка (рис. 4). Сопротивление катушки много меньше сопротивления лампочки.

Рис. 4. Самоиндукция при размыкании цепи

Ключ вначале замкнут. Лампочка не горит — напряжение на ней близко к нулю из-за малости сопротивления катушки. Почти весь ток, идущий в неразветвлённой цепи, проходит через катушку.

При размыкании ключа лампочка ярко вспыхивает! Почему? Ток через катушку начинает резко убывать, и возникает значительная ЭДС индукции, поддерживающая убывающий ток (ведь ЭДС индукции, как видно из (2), пропорциональна скорости изменения тока).

Иными словами, при размыкании ключа в катушке появляется весьма большое вихревое электрическое поле, разгоняющее свободные заряды. Под действием этого вихревого поля через лампочку пробегает импульс тока, и мы видим яркую вспышку. При достаточно большой индуктивности катушки ЭДС индукции может стать существенно больше ЭДС батарейки, и лампочка вовсе перегорит.

Лампочку-то, может, и не жалко, но в промышленности и энергетике данный эффект является серьёзной проблемой. Так как при размыкании цепи ток начинает уменьшаться очень быстро, возникающая в цепи ЭДС индукции может значительно превышать номинальные напряжения и достигать опасно больших величин. Поэтому в агрегатах, потребляющих большой ток, предусмотрены специальные аппаратные меры предосторожности (например, масляные выключатели на электростанциях), препятствующие моментальному размыканию цепи.

Электромеханическая аналогия

Нетрудно заметить определённую аналогию между индуктивностью в электродинамике и массой в механике.

1. Чтобы разогнать тело до заданной скорости, требуется некоторое время — мгновенно изменить скорость тела не получается. При неизменной силе, приложенной к телу, это время тем больше, чем больше масса тела.

Чтобы ток в катушке достиг своего максимального значения, требуется некоторое время; мгновенно ток не устанавливается. Время установления тока тем больше, чем больше индуктивность катушки.

2. Если тело налетает на неподвижную стену, то скорость тела уменьшается очень быстро. Стена принимает на себя удар, и его разрушительное действие тем сильнее, чем больше масса тела.

При размыкании цепи с катушкой ток уменьшается очень быстро. Цепь принимает на себя «удар» в виде вихревого электрического поля, порождаемого убывающим магнитным полем тока, и этот «удар» тем сильнее, чем больше индуктивность катушки. ЭДС индукции может достичь столь больших величин, что пробой воздушного промежутка выведет из строя оборудование.

На самом деле эти электромеханические аналогии простираются довольно далеко; они касаются не только индуктивности и массы, но и других величин, и оказываются весьма полезными на практике. Мы ещё поговорим об этом в листке про электромагнитные колебания.

Энергия магнитного поля

Вспомним второй опыт с лампочкой, которая не горит при замкнутом ключе и ярко вспыхивает при размыкании цепи. Мы непосредственно наблюдаем, что после размыкания ключа в лампочке выделяется энергия. Но откуда эта энергия берётся?

Берётся она, ясное дело, из катушки — больше неоткуда. Но что за энергия была запасена в катушке и как вычислить эту энергию? Чтобы понять это, продолжим нашу электромеханическую аналогию между индуктивностью и массой.

Чтобы разогнать тело массы из состояния покоя до скорости , внешняя сила должна совершить работу . Тело приобретает кинетическую энергию, которая равна затраченной работе: .

Чтобы после замыкания цепи ток в катушке индуктивности достиг величины , источник тока должен совершить работу по преодолению вихревого электрического поля, направленного против тока. Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).

Индуктивность служит аналогом массы ; сила тока является очевидным аналогом скорости . Поэтому естественно предположить, что для энергии магнитного поля катушки может иметь место формула, аналогичная выражению для кинетической энергии:

$W = frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$ (3)

(тем более, что правая часть данной формулы имеет размерность энергии — проверьте!).

Формула (3) действительно оказывается справедливой. Уметь её выводить пока не обязательно, но если вы знаете, что такое интеграл, то вам не составит труда понять следующие рассуждения.

Пусть в данный момент сила тока через катушку равна . Возьмём малый промежуток времени . В течение этого промежутка приращение силы тока равно ; величина считается настолько малой, что много меньше, чем .

За время по цепи проходит заряд dq=Idt . Вихревое электрическое поле совершает при этом отрицательную работу:

$dA_B = mathcal E_i dq = mathcal E_i Idt = -L frac{displaystyle dI}{displaystyle dt vphantom{1^a}}Idt=-LIdI.$

Источник тока совершает такую же по модулю положительную работу (сопротивлением катушки, напомним, мы пренебрегаем, так что вся работа источника совершается против вихревого поля):

Интегрируя это от нуля до , найдем работу источника , которая затрачивается на создание тока :

$A = int_{0}^{I}LIdI=frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$

Эта работа превращается в энергию магнитного поля созданного тока, и мы приходим к формуле (3).

Разберем задачи ЕГЭ по физике по темам: «Самоиндукция», «Магнитный поток», «Индуктивность», «Электромагнитная индукция».

Задача 1. На катушке сопротивлением 8,2 Ом и индуктивностью 25 мГн поддерживается постоянное напряжение 55 В. Сколько энергии выделится при размыкании цепи? Какая средняя ЭДС самоиндукции появится при этом в катушке, если энергия будет выделяться в течение 12 мс?

Дано:

R = 8,2 Ом;
L= 25 мГн = $25cdot 10^{-3}$ Гн;
t = 12 мс = 12;

Найти:
W_м — ? E_is — ?

Решение:

Решение любой задачи по физике должно начинаться с создания модели, которая поясняет ситуацию, описанную в данной задачи. В качестве модели может выступать чертеж, пояснительный рисунок, электрическая схема.

Для этой задачи необходимо начертить электрическую схему.

На схеме изображены катушка индуктивности, источник тока, поддерживающий на ней постоянное напряжение, ключ.

При замкнутом ключе через катушку протекает постоянный электрический ток, величину которого можно рассчитать, используя закон Ома для участка цепи. Катушка аналогична резистору, подключенному в эту цепь.

$displaystyle I=frac{U}{R}, I=frac{55}{8,2}approx 6,7(A).$

Энергия магнитного поля рассчитывается по формуле:

$displaystyle W_{M}=frac{Li^{2}}{2}, W_{M}=frac{25cdot 10^{-3}cdot 6,7^{2}}{2}approx 0,56$ (Дж).

Стоит обратить внимание, что эта формула аналогична формуле кинетической энергии в механике: $displaystyle E_{K}=frac{mv^{2}}{2}.$

При размыкании ключа, через катушку начинает протекать уже переменный ток. Поэтому магнитный поток, пронизывающий катушку, меняется. В самой катушке возникает ЭДС индукции, так как в ней течёт переменный ток. Тем самым, возникает явление самоиндукции.

Используя закон электромагнитной индукции в виде $displaystyle mathcal E _{is}=-Lfrac{Delta I}{Delta t},$ приходим к расчету второй неизвестной величины этой задачи:

$displaystyle mathcal E _{is}=25cdot 10^{-3}frac{6,7}{12cdot 10^{-3}}approx 14$ (B).

В этих расчетах мы не учитывали знак (-), который указан в законе электромагнитной индукции. Смысл этого знака заключен в учёте правила Ленца, определяющего направление индукционного тока. Но так как о направлении индукционного тока речь в задаче не идет, то в расчетах именно получено значение модуля ЭДС самоиндукции.

Ответ: 0,56 Дж, 14 В.

Задача 2. На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 5 до 15 с. Ответ выразите в мкВ.

Решение

Решение любых графических задач необходимо начинать с «чтения» самого графика. В этой задаче рассматривается зависимость силы тока от времени в цепи, содержащей катушку индуктивности. Необходимо обратить внимание на те интервалы времени, в течение которых происходит изменение силы тока. С изменением этой величины связано изменение магнитного потока и, как следствие, возникновение ЭДС самоиндукции. Сила тока меняется в интервале от 0 до 5 с, от 5 до 10 с и от 15 до 20 с. В интервале от 10 до 15 с сила тока постоянна, изменение магнитного потока не происходит, поэтому $mathcal E _{si}=0$ . Для участка от 5 до 10 с надо применить закон электромагнитной индукции $displaystyle mathcal E _{is}=-Lfrac{Delta I}{Delta t}$ .

Для модуля ЭДС самоиндукции, т.е. без учета направления индукционного тока, этот закон будет иметь вид:

$displaystyle |mathcal E _{is}|=left|Lfrac{Delta I}{Delta t} right|$ .

Данные для расчета необходимо взять из графической зависимости, учитывая при этом перевод в систему «СИ».

$displaystyle mathcal E_{is}=left| 1cdot 10^{-3} frac{20cdot 10^{-3}-30cdot 10^{-3}}{10-5}right|=2cdot 10^{-6}(B)=2$ (мкВ).

Ответ: 2 мкВ.

Задача 3. Катушка, обладающая индуктивностью , соединена с источником питания с ЭДС и двумя одинаковыми резисторами . Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.

В момент времени t=0 ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения — $I_{1}.$ Определите значение силы тока $I_{1}.$ Внутренним сопротивлением источника тока пренебречь.

Решение

В данной задаче необходимо рассмотреть две ситуации, которые происходят до и после замыкания ключа.

До замыкания ключа в цепи устанавливается постоянная сила тока, которая определяется законом Ома для полной цепи $displaystyle I=frac{mathcal E}{R+r}$ . Так как по условию внутренним сопротивлением источника можно пренебречь, то $displaystyle I=frac{mathcal E}{R}=3$ (A).
После замыкания ключа параллельно к первому резистору подключается второй, имеющий такое же сопротивление. Тогда общее сопротивление цепи можно рассчитать, как $displaystyle frac{1}{R_{ob}}=frac{1}{R}+frac{1}{R}=frac{2}{R}; R_{ob}=frac{R}{2}.$ Таким образом, внешнее сопротивление цепи уменьшается в 2 раза.
Наличие в цепи катушки индуктивности, в которой возникает ЭДС самоиндукции, препятствует мгновенному нарастанию силы тока (по аналогии с механикой – тело большой массы не может быстро изменить свою скорость). Поэтому сила тока плавно увеличивается до некоторого значения $I_{1}.$
Так как ЭДС самоиндукции с течением времени уменьшается до нулевого значения, то ток в цепи будет возрастать в 2 раза, так как общее сопротивление уменьшается также в 2 раза.
$displaystyle I_{1}=frac{mathcal E}{R/2}=frac{2mathcal E}{R}=6$ (A).

Ответ: 6 А.

Задача 4. Катушка Проволочная рамка площадью 60 см² помещена в однородное магнитное поле так, что плоскость рамки перпендикулярна вектору индукции vec{B} . Проекция $B_{n}$ индукции магнитного поля на нормаль к плоскости рамки изменяется во времени t согласно графику на рисунке.

Из приведенного ниже списка выберите все верные утверждения о процессах, происходящих в рамке.

Модуль ЭДС электромагнитной индукции, возникающий в рамке, максимален в интервале от 0 до 1мс.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
Т.е. максимальное значение ЭДС индукции будет наблюдаться на интервале максимального изменения $B_{n}$ с течением времени. В интервале от 0 до 1 мс скорость изменения проекции $B_{n}$ наибольшая.
Утверждение верное.
Магнитный поток через рамку в интервале от 2 до 4 мс равен 12 мВб.
Ответ. Формула для расчета магнитного потока имеет вид $Phi=B_{n}S.$
В данном временном интервале проекция $B_{n}$ постоянна и равна 2 Тл.
$displaystyle Phi=2cdot 60cdot 10^{-4}=12cdot 10^{-3}$ (Вб) = 12 (мВб).
Утверждение верное.
Модуль ЭДС электромагнитной индукции, возникающей в рамке, в интервале от 4 до 6 мс равен 6 В.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
$displaystyle mathcal E=left|frac{(-2-2)cdot 60cdot 10^{-4}}{2cdot 10^{-3}}right|=12$ (B).
Утверждение неверное.
Модуль скорости изменения магнитного потока через рамку минимален в интервале от 0 до 1 мс.
Ответ. В той задаче изменение магнитного потока связано с изменением проекции $B_{n}$ индукции магнитного поля. В интервале от 0 до 1 мс проекция $B_{n}$ меняется быстрее всего, потому и изменение магнитного потока максимальное.
Утверждение неверное.
Модуль ЭДС электромагнитной индукции, возникающей в рамке, равен нулю в интервале времени от 2 до 4 мс.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
В интервале от 2 до 4 мс проекция $B_{n}$ не изменяется, потому и .
Тогда в проволочной рамке ЭДС индукции не возникает.
Утверждение верное.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Самоиндукция» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

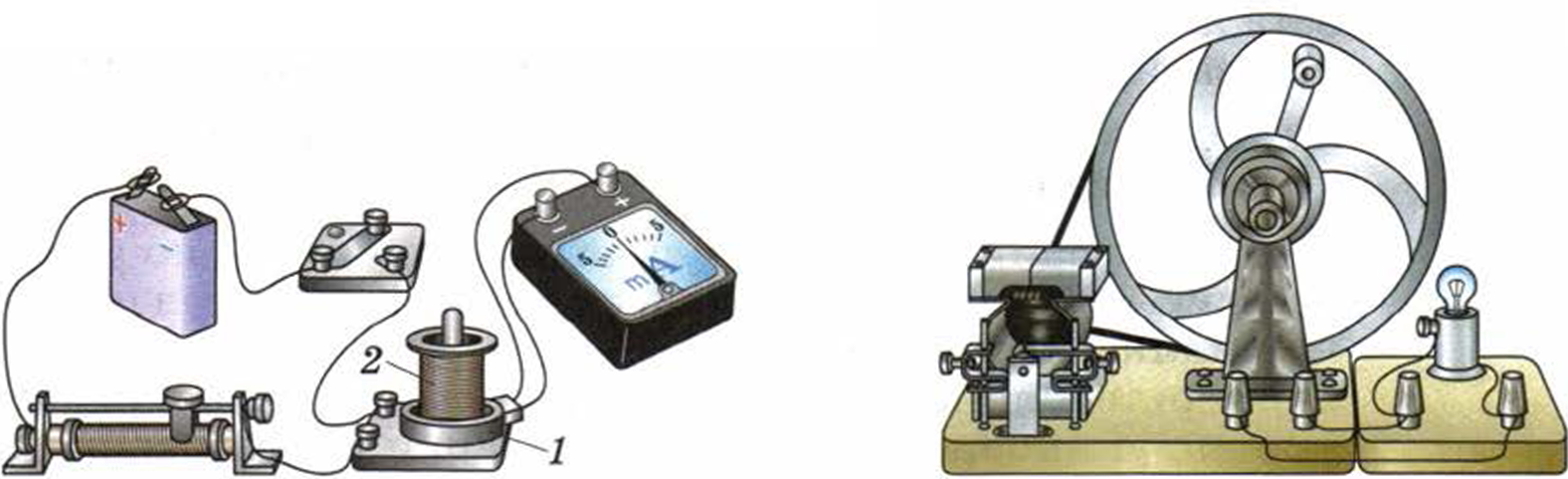
Цель работы: Изучить явление электромагнитной индукции.
Оборудование: Миллиамперметр, катушка-моток, магнит дугообразный, источник питания, катушка с железным сердечником от разборного электромагнита, реостат, ключ, провода соединительные, модель генератора электрического тока (одна на класс).
Указания к работе:
1. Подключите катушку-моток к зажимам миллиамперметра.
2. Наблюдая за показаниями миллиамперметра, подводите один из полюсов магнита к катушке, потом на несколько секунд остановите магнит, а затем вновь приближайте его к катушке, вдвигая в неё (рис. 196). Запишите, возникал ли в катушке индукционный ток во время движения магнита относительно катушки; во время его остановки.

Запишите, менялся ли магнитный поток Ф, пронизывающий катушку, во время движения магнита; во время его остановки.
4.     На основании ваших ответов на предыдущий вопрос сделайте и запишите вывод о том, при каком условии в катушке возникал индукционный ток.
5.     Почему при приближении магнита к катушке магнитный поток, пронизывающий эту катушку, менялся? (Для ответа на этот вопрос вспомните, во-первых, от каких величин зависит магнитный поток Ф и, во-вторых, одинаков
ли модуль вектора индукции В магнитного поля постоянного магнита вблизи этого магнита и вдали от него.)
6.     О направлении тока в катушке можно судить по тому, в какую сторону от нулевого деления отклоняется стрелка миллиамперметра.
Проверьте, одинаковым или различным будет направление индукционного тока в катушке при приближении к ней и удалении от неё одного и того же полюса магнита.

4.      Приближайте полюс магнита к катушке с такой скоростью, чтобы стрелка миллиамперметра отклонялась не более чем на половину предельного значения его шкалы.
Повторите тот же опыт, но при большей скорости движения магнита, чем в первом случае.
При большей или меньшей скорости движения магнита относительно катушки магнитный поток Ф, пронизывающий эту катушку, менялся быстрее?
При быстром или медленном изменении магнитного потока сквозь катушку сила тока в ней была больше?
На основании вашего ответа на последний вопрос сделайте и запишите вывод о том, как зависит модуль силы индукционного тока, возникающего в катушке, от скорости изменения магнитного потока Ф, пронизывающего этукатушку.
5.      Соберите установку для опыта по рисунку 197.
6.      Проверьте, возникает ли в катушке-мотке 1 индукционный ток в следующих случаях:
а) при замыкании и размыкании цепи, в которую включена катушка 2;
б) при протекании через катушку 2 постоянного тока;
в) при увеличении и уменьшении силы тока, протекающего через катушку 2, путём перемещения в соответствующую сторону движка реостата.
10. В каких из перечисленных в пункте 9 случаев меняется магнитный поток, пронизывающий катушку 1? Почему он меняется?
11. Пронаблюдайте возникновение электрического тока в модели генератора (рис. 198). Объясните, почему в рамке, вращающейся в магнитном поле, возникает индукционный ток.
  Рис. 196

Рис. 197 Рис. 198

Источник

Электромагнитная индукция

Содержание

Явление электромагнитной индукции
Магнитный поток
Закон электромагнитной индукции Фарадея
Правило Ленца
Самоиндукция
Индуктивность
Энергия магнитного поля
Основные формулы раздела «Электромагнитная индукция»

Явление электромагнитной индукции

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Объяснения возникновения индукционного тока

Свойства вихревого электрического поля:

источник – переменное магнитное поле;
обнаруживается по действию на заряд;
не является потенциальным;
линии поля замкнутые.

Магнитный поток

Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

Если контур состоит из ( N ) витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):

При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:

где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Алгоритм решения задач с использованием правила Ленца:

определить направление линий магнитной индукции внешнего магнитного поля;
выяснить, как изменяется магнитный поток;
определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Энергия магнитного поля

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

2. Записать формулу:

закона электромагнитной индукции;
ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.

Электромагнитная индукция

3.2 (63.64%) 99 votes

Источник

Магнитный поток, проходящий через площадь S равен:

Ф = BScosα;

где:

Ф ― величина магнитного потока [Вб],

S ― площадь контура [м2],

B ― индукция магнитного поля [Тл],

α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.

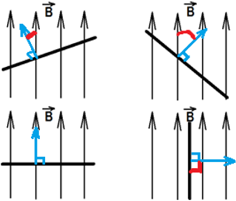
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:

Ф = BScos90° = BS;

Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

где:

$varepsilon_i $ ― ЭДС электромагнитной индукции [B],

$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],

∆Ф ― изменение магнитного потока [Вб],

∆t ― время, за которое происходит это изменение [c].

Кроме того, ЭДС индукции равна производной магнитного потока по времени:

$varepsilon_i = -text{Ф}_t’$

где:

― ЭДС электромагнитной индукции [B],
― производная магнитного потока по времени [Вб/с].

Задача 1

Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?

Решение:

Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.

Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.

По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$

И это очень важный момент, без которого мы не сможем решить такого рода задачу.

Теперь посчитаем ЭДС индукции.

Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса

$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.

Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$

Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).

Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.

По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.

Мы получили зависимость силы тока от времени.

Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.

В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.

Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.

Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$

Ответ: 0,002

Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:

увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
изменением направления вектора магнитного поля (т. е. изменением угла α);
деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
изменением нескольких из этих величин одновременно.

Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.

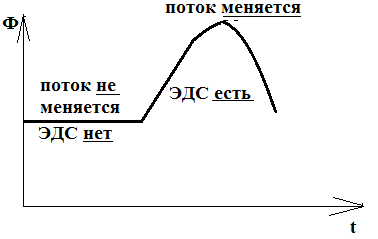
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:

Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Задача 2

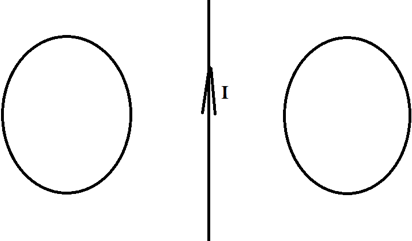
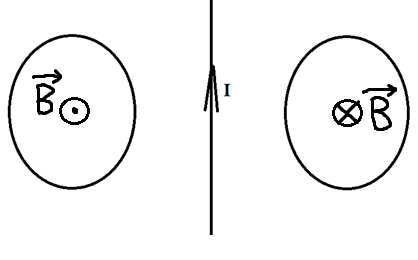
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?

Решение:

Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?

Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.

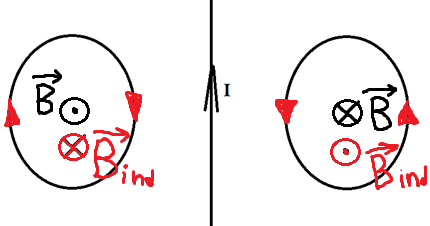
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?

Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.

Движение проводников

Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).

Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;

где:

$varepsilon_i$― ЭДС электромагнитной индукции [B],

B ― индукция магнитного поля [Тл],

l ― длина проводника [м],

v ― скорость движения проводника [м/с],

α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$

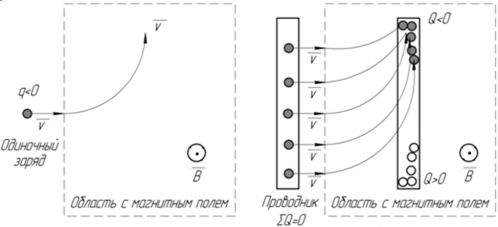
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.

В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.

На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.

В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;

где:

U — разность потенциалов [В],

l — длина проводника [м],

v — скорость движения проводника $big[ frac{text{м}}{c} big]$

B — индукция магнитного поля [Тл],

α — угол между направлением скорости и длиной проводника.

В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.

В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = — frac{Delta text{Ф}}{Delta t}$

В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.

Задача 3

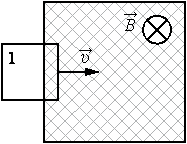
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

Решение:

Составим цепочку.

Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.

Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.

А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.

Пройдёмся вдоль этой цепочки.

Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$

Ответ: 1

Источник

Явление электромагнитной индукции

Магнитный поток

Закон электромагнитной индукции Фарадея

Правило Ленца

Самоиндукция

Индуктивность

Энергия магнитного поля

Основные формулы раздела «Электромагнитная индукция»

Самоиндукция

Темы кодификатора ЕГЭ: самоиндукция, индуктивность, энергия магнитного поля.

Индуктивность

Электромеханическая аналогия

Энергия магнитного поля

Электромагнитная индукция

Явление электромагнитной индукции

Магнитный поток

Закон электромагнитной индукции Фарадея

Правило Ленца

Самоиндукция

Индуктивность

Энергия магнитного поля

Основные формулы раздела «Электромагнитная индукция»

Не пропустите также: