Введение в модулярную арифметику
Время на прочтение
6 мин
Количество просмотров 67K
В обычной жизни мы обычно пользуемся позиционной системой счисления. В позиционной системе счисления значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда) [1]. Однако существуют и так называемые «непозиционные системы счисления», к одной из которых относится «система остаточных классов» (СОК) (или в оригинале Residue Number System (RNS)), являющаяся основой модулярной арифметики. Модулярная арифметика базируется на «Китайской теореме об остатках» [2], которая для нашего случая звучит следующим образом:
Для любой системы взаимно простых чисел p1, … pn, любое число X из диапазона [0; M), где M = p1*p2*…*pn взаимооднозначно представимо в виде вектора (a1, a2, …, an), где ai = X%pi (здесь и далее «%» — операция взятия остатка от целочисленного деления X на pi).
p1, … pn – модули системы
a1, a2, …, an – остатки (вычеты) числа по заданной системе модулей
На первый взгляд непонятно какое преимущество может дать такая система, однако существует 2 свойства, которые позволяют эффективно использовать модулярную арифметику в некоторых областях микроэлектроники:
- Отсутствие переноса разрядов в сложении и умножении. Пусть нам дано два числа X1 и X2, представленные в виде системы остатков (x11, x12, …, x1n) и (x21, x22, …, x2n) по системе взаимнопростых чисел (p1, p2, …, pn). В этом случае:
X3 = X1 + X2 = ((x11+x21)%p1, (x12+x22)%p2, …, (x1n+x2n)%pn)
X4 = X1 * X2 = ((x11*x21)%p1, (x12*x22)%p2, …, (x1n*x2n)%pn)
То есть что бы сложить или умножить два числа, достаточно сложить или умножить соответствующие элементы вектора, что для микроэлектроники означает, что это можно сделать параллельно и из-за малых размерностей p1, p2, …, pn сделать очень быстро. - Ошибка в одной позиции вектора не влияет на расчеты в других позициях вектора. В отличие от позиционной системы счисления все элементы вектора равнозначны и ошибка в одном из них ведет всего лишь к сокращению динамического диапазона. Этот факт позволяет проектировать устройства с повышенной отказоустойчивостью и коррекцией ошибок.
Но не всё так гладко, как хотелось бы. В отличие от позиционной системы счисления, следующие операции (называемые «немодульными») выполняются сложнее, чем в позиционной системе счисления: сравнение чисел, контроль переполнения, деление, квадратный корень и.т.д. Первые успешные попытки применения модулярной арифметики в микроэлектронике были предприняты ещё в 1950-х годах, но из-за сложностей с немодульными операциями интерес несколько утих. Однако в настоящее время модулярная арифметика снова возвращается в микроэлектронику по следующим причинам:
- большое распространение мобильных процессоров, в которых требуется высокая скорость при маленьком потреблении энергии. Отсутствие переноса в арифметических операциях сложения/умножения позволяет снизить потребление энергии.
- увеличивающаяся плотность элементов на кристалле в некоторых случаях не позволяет провести полное тестирование, поэтому растет важность устойчивости процессоров к возможным ошибкам.
- появление специализированных процессоров с большим числом операций над векторами, которые требуют высокой скорости и включают в себя преимущественно сложение и умножение чисел (как пример умножение матриц, скалярное произведение векторов, преобразования Фурье и.т.д).
В данный момент модулярная арифметика применяется в следующих областях: цифровая обработка сигналов, криптография, обработка изображений/аудио/видео и.т.д.
Прямое преобразование
Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.
Пример: Пусть требуется найти представление числа X = 25 по системе модулей (3, 5, 7). X = (25%3, 25%5, 25%7) = (1, 0, 4).
Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p
Любое число X можно записать в виде X%p = (xn-1*2n-1 + xn-2*2n-2 + x0*20)%p = ((xn-1)%p*2n-1%p) + ((xn-2)%p*2n-2%p) + … + x0%p)%p. Поскольку в данном случае xn-1, … x0 равны 0 или 1, то фактически нам требуется сложить вычеты вида (2i%p).
Пример: пусть задано число 25 или в двоичной системе счисления 11001 и требуется найти остаток по модулю 7.
25%7 = (1*24 + 1*23 + 0*22 + 0*1 + 1*20)%7 = (24%7 + 23%7 + 1%7)%7 = (2 + 1 + 1)%7 = 4
Систему используемых модулей подбирают под конкретную задачу. Например, для представления 32-х битных чисел достаточно следующей системы модулей: (7, 11, 13, 17, 19, 23, 29, 31) – все они взаимнопросты друг с другом, их произведение равно 6685349671 > 4294967296. Каждый из модулей не превышает 5 бит, то есть операции сложения и умножения будут производиться над 5-битными числами.
Особое значение так же имеет система модулей вида: (2n-1, 2n, 2n+1) в связи с тем, что прямое и обратное преобразование для них выполняется простейшим образом. Что бы получить остаток от деления на 2n достаточно взять последние n цифр двоичного представления числа.
Арифметические операции
Пример: пусть задана система модулей (3, 5, 7), то есть мы можем выполнять операции, результат которых не превышает 3*5*7 = 105. Умножим два числа 8 и 10.
8 = (8%3, 8%5, 8%7) = (2, 3, 1)
10 = (10%3, 10%5, 10%7) = (1, 0, 3)
8*10 = ((2*1)%3, (3*0)%5, (1*3)%7) = (2, 0, 3)
Проверяем
80 = (80%3, 80%5, 80%7) = (2, 0, 3)
Обратное преобразование
Обратное преобразование из системы счисления в остаточных классах в позиционную систему счисления производится одним из двух способов:
- На базе Китайской теоремы об остатках или системы ортогональных базисов
- На базе полиадического кода (другие названия mixed-radix system, система, со смешанным основанием)
Остальные предложенные в различной литературе способы, по сути, являются смесью этих двух.
Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x1, x2, … xn) = (x1, 0, …, 0) + (0, x2, …, 0) + … + (0, 0, …., xn) = x1*(1, 0, …, 0) + x2*(0, 1, …, 0) + … + xn*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (Mi*bi)%pi = 1, где Mi = M/pi, а bi – искомое число. В этом случае позиционное представление Bi = Mi*bi и
X = (x1*(M1*b1) + x2*(M2*b2) + … + xn*(Mn*bn))%M
Пример: пусть задана система модулей (3, 5, 7), найдем значения Mi и bi (0 < i <= 3)
M = 3*5*7 = 105
M1 = 105/3 = 35
M2 = 105/5 = 21
M3 = 105/7 = 15
(35*b1)%3 = 1 => b1 = 2
(21*b2)%5 = 1 => b2 = 1
(15*b3)%7 = 1 => b3 = 1
Теперь преобразуем какое-нибудь число в системе остаточных классов. Положим
X = (2, 3, 1) = (2*35*2 + 3*21*1 + 1*15*1)%105 = (140 + 63 + 15)%105 = 218%105 = 8
Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M1, …, Mn), а так же операция взятия остатка по модулю большого числа M.
Способ на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел p1, … pn, как [4]:
X = a1 + a2*p1 + a3*p1*p2 +… + an-1*p1*p2*…*pn-2 + an*p1*p2*…*pn-1, где 0 < ai < pi
- X%p1 = x1 = a1
- (X – a1)%p2 = (x2 — a1)%p2 = (a2*p1)%p2 => a2 = ((p1-1)%p2*(x2 — a1))%p2
- (X — a1 — a2*p1)%p3 = (a3*p1*p2)%p3 => a3 = ((p2-1)%p3*((p1-1)%p3*(x3 — a1) — a2))%p3
- …
Для использования этого метода требуются константы вида (pi-1)%pk-1. Можно также заметить, что начинать вычисление a3 можно, как только появилось значение a1. На основе этого метода можно строить конвеерные преобразователи.
Пример: Рассмотрим тот же пример — найдем позиционное представление числа X = (2, 3, 1) в системе модулей (3, 5, 7)
- a1 = x1 = 2
- a2 = ((p1-1)%p2*(x2 — a1))%p2 = ((3-1)%5*(3 — 2))%5 = 2*1 = 2
- a3 = ((p2-1)%p3*((p1-1)%p3*(x3 — a1) — a2))%p3 = ((5-1)%7*((3-1)%7*(1 — 2) — 2))%7 = (3*(5*(1-2)-2))%7 = (3*(-7))%7 = 0
- X = a1 + a2*p1 + a3*p1*p2 = a1 + 3*a2 + 15*a3 = 2 + 3*2 + 15*0 = 8
Замечание: что бы найти константу вида (3-1)%5 требуется решить уравнение (3*x)%5 = 1, где 0 <= x < 5
P.S.
Статья написана несколько сумбурно, потому что тема достаточно большая и в одну статью вместить все не представляется возможным. В следующих статьях я попробую расписать более подробно различные аспекты модулярной арифметики. На Хабре же я не нашел вообще ничего что относится к этой теме, только краткие упоминания в других статьях, поэтому и было решено написать небольшой обзор с простенькими примерами. Для тех, кого тема заинтересовала, рекомендую прочитать книгу номер [3] из списка литературы (на английском языке), она написана доступным языком с большим количеством примеров.
Литература
[1] ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%B7%D0%B8%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
[2] ru.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%B0%D1%85
[3] Amos Omondi, Benjamin Premkumar, Residue Number Systems: Theory and Implementation, 2007.
[4] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.
Двоичное число: прямой, обратный и дополнительный коды
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа
Прямой, обратный и дополнительный коды двоичного числа — способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел
Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Прямой код — способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел
Прямой код используется в двух вариантах.
В первом (основной) — для записи только неотрицательных чисел:
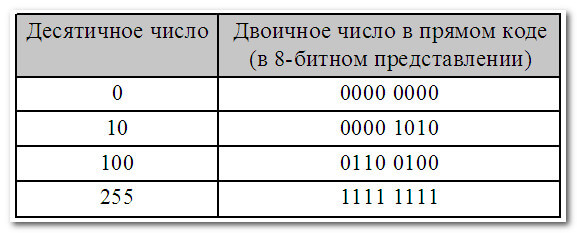
Второй вариант — для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
— знаковый разряд равен 0, то число положительное
— знаковый разряд равен 1, то число отрицательное
В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:
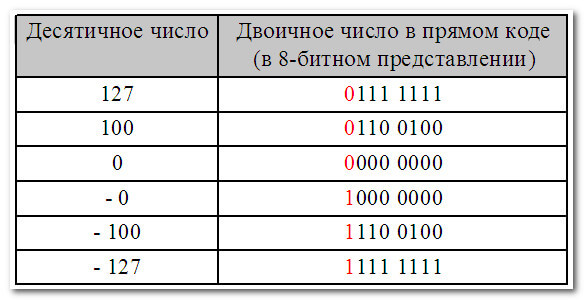
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):
Обратный код
Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 1, за которым следует инвертированное значение положительного числа.
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
При 8-битном двоичном числе — знаковый бит (как и в прямом коде) старший (8-й)
Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127
Арифметические операции с отрицательными числами в обратном коде:
(Арифметические операции с двоичными числами)
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = — 0001 1001
Необходимо их сложить:
100 + (-25) = 100 — 25 = 75
1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд — переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = — 0000 1010
Необходимо их сложить:
5 + (-10) = 5 — 10 = -5
1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)
2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 —-> 1000 0101
Проверяем:
1000 0101 = — 0000 0101 = -5
Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
— арифметические операции проводятся в два этапа
— как и в прямом коде два представления нуля — положительный и отрицательный
Дополнительный код
Дополнительный код — наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.
Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
— инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
— к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 — десятичное число -10 в дополнительном коде
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 — 0000 1010 = 1111 0110 — десятичное число -10 в дополнительном коде
Арифметические операции с отрицательными числами в дополнительном коде
Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде
Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода
Предыдущие статьи:
1. Микроконтроллеры — первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции

Загрузка…
Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:
- не требовал усложнения архитектуры процессора для выполнения арифметических операций с отрицательными числами,
- не усложнял арифметические действия,
- хранил бы одинаковое количество положительных и отрицательных чисел.
Рассмотрим разные методы представления.
Содержание
- 1 Прямой код
- 1.1 Достоинства представления чисел с помощью прямого кода
- 1.2 Недостатки представления чисел с помощью прямого кода
- 2 Код со сдвигом
- 2.1 Достоинства представления чисел с помощью кода со сдвигом
- 2.2 Недостатки представления чисел с помощью кода со сдвигом
- 3 Дополнительный код (дополнение до единицы)
- 3.1 Достоинства представления чисел с помощью кода с дополнением до единицы
- 3.2 Недостатки представления чисел с помощью кода с дополнением до единицы
- 4 Дополнительный код (дополнение до двух)
- 4.1 Длинная арифметика для чисел, представленных с помощью кода с дополнением до двух
- 4.2 Достоинства представления чисел с помощью кода с дополнением до двух
- 4.3 Недостатки представления чисел с помощью кода с дополнением до двух
- 5 См. также
- 6 Источники информации
Прямой код
Нумерация двоичных чисел в прямом представлении
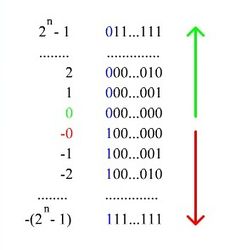
При записи числа в прямом коде (англ. Signed magnitude representation) старший разряд является знаковым разрядом. Если его значение равно нулю, то представлено положительное число или положительный ноль, если единице, то представлено отрицательное число или отрицательный ноль. В остальных разрядах (которые называются цифровыми) записывается двоичное представление модуля числа. Например, число в восьмибитном типе данных, использующем прямой код, будет выглядеть так: .
Таким способом в -битовом типе данных можно представить диапазон чисел .
Достоинства представления чисел с помощью прямого кода
- Получить прямой код числа достаточно просто.
- Из-за того, что обозначает , коды положительных чисел относительно беззнакового кодирования остаются неизменными.
- Количество положительных чисел равно количеству отрицательных.
Недостатки представления чисел с помощью прямого кода
- Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого).
- Существуют два нуля: и , из-за чего усложняется арифметическое сравнение.
Из-за весьма существенных недостатков прямой код используется очень редко.
Код со сдвигом
Код со сдвигом. Как видно, двоичное представление зациклено по модулю ( нулей)
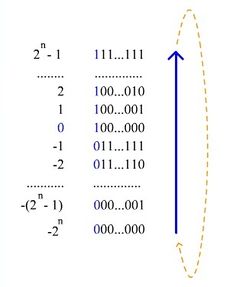
При использовании кода со сдвигом (англ. Offset binary) целочисленный отрезок от нуля до ( — количество бит) сдвигается влево на , а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от до . Например, число в восьмибитном типе данных, использующем код со сдвигом, превратится в , то есть будет выглядеть так: .
По сути, при таком кодировании:
- к кодируемому числу прибавляют ;
- переводят получившееся число в двоичную систему исчисления.
Можно получить диапазон значений .
Достоинства представления чисел с помощью кода со сдвигом
- Не требуется усложнение архитектуры процессора.
- Нет проблемы двух нулей.
Недостатки представления чисел с помощью кода со сдвигом
- При арифметических операциях нужно учитывать смещение, то есть проделывать на одно действие больше (например, после «обычного» сложения двух чисел у результата будет двойное смещение, одно из которых необходимо вычесть).
- Ряд положительных и отрицательных чисел несимметричен.
Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.
Дополнительный код (дополнение до единицы)
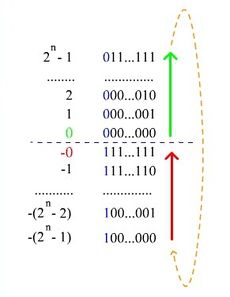
Нумерация двоичных чисел в представлении c дополнением до единицы. В отличии от кода со сдвигом, нулю соответствуют коды и
В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones’ complement).
Алгоритм получения кода числа:
- если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число;
- если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код);
- если число является нулем, то его можно представить двумя способами: или .
Пример: переведём число в двоичный восьмибитный код. Прямой код модуля : , инвертируем и получаем .
Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода.
Таким способом можно получить диапазон значений .
Достоинства представления чисел с помощью кода с дополнением до единицы
- Простое получение кода отрицательных чисел.
- Из-за того, что обозначает , коды положительных чисел относительно беззнакового кодирования остаются неизменными.
- Количество положительных чисел равно количеству отрицательных.
Недостатки представления чисел с помощью кода с дополнением до единицы
- Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора.
- Существуют два нуля: и .
Дополнительный код (дополнение до двух)
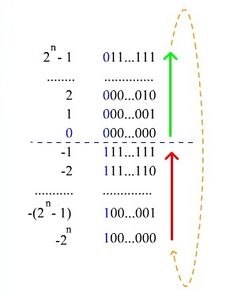
Нумерация двоичных чисел в представлении c дополнением до двух.
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two’s complement).
Алгоритм получения дополнительного кода числа:
- если число неотрицательное, то в старший разряд записывается ноль, далее записывается само число;
- если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице.
В качестве примера переведём число в дополнительный восьмибитный код. Прямой код модуля : , обратный — , прибавляем , получаем , приписываем в качестве знакового разряда, в результате получаем .
Также дополнительный код отрицательного числа , хранящегося в битах, равен . По сути, дополнительный код представляет собой дополнение до : так как в -разрядной арифметике (двоичная запись этого числа состоит из единицы и нулей, а в -разрядную ячейку помещаются только младших разрядов, то есть нулей), то верно равенство .
Для получения из дополнительного кода самого числа нужно инвертировать все разряды кода и прибавить к нему единицу. Можно проверить правильность, сложив дополнительный код с самим числом: результат должен быть равен . Переведём обратно. Инвертируем — , прибавляем , получаем — модуль исходного числа . Проверим: .
Можно получить диапазон значений .
Длинная арифметика для чисел, представленных с помощью кода с дополнением до двух
Дополнительный код также удобно использовать для вычислений в длинной арифметике, особенно для операций сложения и вычитания. Это операции удобно выполнять с числами одинаковой длины, поэтому в старшие разряды меньшего числа нужно поместить нули (если число положительно) или единицы (если число отрицательно). Тогда числа будут выглядеть следующим образом: в старших разрядах бесконечное число нулей (единиц), а в младших разрядах уже встречаются и нули, и единицы, которые кодируют само число, а не знак. Удобство заключается в том, что нам не обязательно проделывать операции сложения с каждой парой бит, если мы знаем, что на этом отрезке в числах стоят либо единицы, либо нули. Таким образом, на этом отрезке в получившемся числе тоже будут либо только единицы, либо только нули. Операцию сложения можно выполнить только один раз для старших битов, таким образом мы узнаем знак получившегося числа. Вычитание тоже выполняется просто: инвертируем число, прибавляем один и получаем это число с минусом, затем просто делаем сложение.
Однако умножение с числами, представленными дополнительным кодом, выполнять не всегда оптимально: алгоритм либо слишком медленный (наивный алгоритм работает за ), либо слишком сложный. Лучше для умножение использовать прямой код (бит под знак). Тогда можно числа перевести в десятичную систему счисления, выполнить быстрое преобразование Фурье за , затем перевести их обратно в двоичную. Обычно такой алгоритм работает быстрее, чем выполнение операции напрямую с двоичными числами. Для деления обычно тоже лучше использовать прямой код.
Достоинства представления чисел с помощью кода с дополнением до двух
- Возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие.
- Нет проблемы двух нулей.
Недостатки представления чисел с помощью кода с дополнением до двух
- Ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел.
- В отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности.
Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.
См. также
- Представление вещественных чисел
- Представление символов, таблицы кодировок
Источники информации
- Эндрю Таненбаум «Архитектура компьютера», 5-е изд., стр. 739—741
- Wikipedia — Signed number representations
- Wikipedia — Offset binary
- Википедия — Прямой код
- Википедия — Дополнительный код
ДВОИЧНАЯ АРИФМЕТИКА
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения:
Двоичные операции
|
сложение |
вычитание |
умножение |
|
0+0=0 |
0-0=0 |
0х0=0 |
|
0+1=1 |
1-0=1 |
0х1=0 |
|
1+0=1 |
1-1=0 |
1х0=0 |
|
1+1=0+ед.переноса |
10-1=1 |
1х1=1 |
Правила арифметики во всех позиционных системах аналогичны. При сложении в каждом разряде в соответствии с таблицей двоичного сложения производится сложение двух цифр слагаемых или двух этих цифр и 1, если имеется перенос из соседнего младшего разряда. В результате получается цифра соответствующего разряда суммы и, возможно, также 1 переноса в старший разряд. Приведем пример сложения двух двоичных чисел:
|
Переносы |
|
|
111 |
|
|
110111.01 |
55.25 |
|
+ 10011.10 |
+ 19.5 |
|
1001010.11 |
74.75 |
Справа показано сложение тех же чисел, представленных в десятичной системе.
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из следующего старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда. Заем производится каждый раз, когда цифра в разряде вычитаемого больше цифры в том же разряде уменьшаемого. Поясним сказанное примером:
11011,10
1101,01
1110,01
Умножение двоичных многоразрядных чисел производится путем образования частичных произведений и последующего их суммирования. В соответствии с таблицей двоичного умножения каждое частичное произведение равно 0, если в соответствующем разряде множителя стоит 0, или равно множимому, сдвинутому на соответствующее число разрядов влево, если в разряде множителя стоит 1. Таким образом, операция умножения многоразрядных двоичных чисел сводится к операциям сдвига и сложения. Положение запятой определяется так же, как при умножении десятичных чисел. Сказанное поясняется примером:
1011,1 х 101,01 = 111100,011
10111
х 10101
10111
00000 + 10111 00000 10111____
111100011
Особенности выполнения деления двоичных чисел поясняются следующим примером:
1100,011:10,01 = ? 1100011|10010 —10010 101,1
11011 —10010 10010 —10010 00000
Благодаря простоте правил двоичного сложения, вычитания и умножения применение в ЭВМ двоичной системы счисления позволяет упростить схемы устройств, выполняющих арифметические операции.
ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В КОМПЬЮТЕРЕ
Любая информация (числа, команды, алфавитно-цифровые записи и т. п.) представляется в компьютере в виде двоичных кодов (двоичных слов) фиксированной или переменной длины. Отдельные элементы двоичного кода, имеющие значение 0 или 1, называют разрядами или битами. В компьютере слова часто разбивают на части, называемые байтами. В современных ЭВМ широко используется байт, содержащий 8 бит.
Двоичный разряд представляется в компьютере некоторым техническим устройством, например триггером, двум различным состояниям которого приписывают значения 0 и 1. Набор соответствующего количества таких устройств служит для представления многоразрядного двоичного числа (слова).
В компьютере применяют две формы представления чисел: с фиксированной запятой (точкой) и с плавающей запятой (точкой). Эти формы называют также соответственно естественной и полулогарифмической.
При представлении чисел с фиксированной запятой положение запятой фиксируется в определенном месте относительно разрядов числа. Обычно подразумевается, что запятая находится или перед старшим разрядом, или после младшего. В первом случае могут быть представлены только числа, которые по модулю меньше 1, во втором — только целые числа.

|
Зн |
2-1 |
… |
2-15 |
||
< 2 байта, 16 разрядов >
|
Зн |
2-1 |
… |
2-31 |
|||
< 4 байта, 32 разрядa >
Форматы данных для представления двоичных чисел с фиксированной запятой (точкой)
На рис. 1.1 показаны примеры форматов данных для представления двоичных чисел с фиксированной запятой и соответствующие разрядные сетки. По сложившейся в вычислительной технике традиции нумерация разрядов (бит) в разрядной сетке в машинах общего назначения (ЕС ЭВМ) ведется слева направо, а в малых ЭВМ, микро-ЭВМ и микропроцессорах — справа налево. На разрядной сетке указаны веса разрядов.
При представлении числа со знаком для кода знака выделяется «знаковый» разряд (обычно крайний слева). В этом разряде 0 соответствует плюсу, а 1 — минусу.
На рис. 1.1, a показан формат для чисел с запятой, фиксированной перед старшим разрядом. В этом формате могут быть с точностью до 2–(n-1) представлены числа (правильные дроби) в диапазоне
2–(n-1) |x| 1 — 2–(n-1)
Первые компьютеры были машинами с фиксированной запятой, причем запятая фиксировалась перед старшим разрядом числа. В настоящее время, как правило, форму с фиксированной запятой применяют для представления целых чисел (запятая фиксирована после младшего разряда).
Используют два варианта представления целых чисел: со знаком и без знака. В последнем случае все разряды разрядной сетки служат для представления модуля числа.
Представление чисел с фиксированной запятой используется как основное и единственное лишь в сравнительно небольших по своим вычислительным возможностям машинах, применяемых в системах передачи данных, для управления технологическими процессами и обработки измерительной информации в реальном масштабе времени.
В машинах, предназначенных для решения широкого круга вычислительных задач, основным является представление чисел с плавающей запятой, не требующее масштабирования данных. Однако в таких машинах часто наряду с этой формой представления чисел используется также и представление с фиксированной запятой для целых чисел, поскольку операции с такими числами выполняются за меньшее время. В частности, к операциям с целыми числами сводятся операции над кодами адресов (операции индексной арифметики).
Представление числа с плавающей запятой в общем случае имеет вид
где q — мантисса числа х, sp — характеристика числа х; р — порядок-, s
— основание характеристики (обычно целая степень числа 2).
Мантисса (правильная дробь со знаком) и порядок (целое число со знаком) представляются в системе счисления с основанием, равным s (в соответствующей двоично-кодированной форме). Знак числа совпадает со знаком мантиссы.
Порядок р, который может быть положительным или отрицательным целым числом, определяет положение запятой в числе х.
На рис. 1.2 показаны примеры форматов данных для чисел с плавающей запятой. Одна часть бит формата используется для представления порядка, а другая — для мантиссы.
Арифметические действия над числами с плавающей запятой требуют выполнения помимо операций над мантиссами определенных операций над порядками (сравнение, вычитание и др.). Для упрощения операций над порядками их сводят к действиям над целыми положительными числами (целыми числами без знаков), применяя представление чисел с плавающей запятой со «смещенным порядком».
В случае представления числа с плавающей запятой со смещенным порядком к его порядку р прибавляется целое число — смещение N = 2k, где k
— число двоичных разрядов, используемых для модуля порядка. Смещенный порядок рсм=р+N всегда положителен. Для его представления
необходимо такое же число разрядов, как и для модуля и знака порядка р. Важная особенность смещенных порядков состоит в том, что если для
порядков р’ и р», представляющих собой целые числа со знаками, выполняется соотношение
p’ p»,
то и для положительных целых чисел соответствующих смещенных порядков р’см и р»см всегда р’см р»см . Это представление числа называют также полулогарифмическим, так как часть числа — характеристика — выражена в логарифмической форме.

|
Зн.п |
2ln-2 |
… |
20 |
Зн.m |
2-1 |
2lm |
|||||||||||
|
< |
Код порядка |
> |
< |
Код мантиссы |
> |
||||||||||||
|
< Длина поля порядка |
> |
< Длина поля мантиссы |
> |
Знак ‘-‘ кодируется единицей, знак ‘+’ — нулем.
Представление чисел с плавающей запятой
При фиксированном числе разрядов мантиссы любая величина представляется в машине с наибольшей возможной точностью нормализованным числом.
Число х = s»q называется нормализованным, если мантисса q удовлетворяет условию
т. е. старший разряд мантиссы в s-ричной системе отличен от нуля. В процессе вычислений может получаться ненормализованное число. В этом случае машина, если это предписано командой, автоматически нормализует его («нормализация результата» операции).
Пусть r старших разрядов s-ричной мантиссы равны 0. Тогда нормализация заключается в сдвиге мантиссы на r разрядов влево и уменьшении порядка на r единиц, при этом в младшие r разрядов мантиссы записывается 0. После такой операции число не меняется, а условие (2.4) выполняется. При нулевой мантиссе нормализация невозможна.
В различных ЭВМ применяются представления чисел с плавающей запятой в системах счисления с различными основаниями, но равными целой степени числа 2 (s = 2w), при этом порядок р представляется целым числом, а мантисса q — числом, в котором группы по w двоичных разрядов изображают цифры мантиссы с основанием системы счисления s= 2w.
Примерами применяемых форм чисел с плавающей запятой с различными основаниями системы счисления являются
x=2pq (1 > |q| 1/2); x=8pq (I > |q| 1/8);
x= l6pq (I > |q| 1/16).
Вскобках указаны соответствующие условия получения нормализованных чисел.
Использование для чисел с плавающей запятой недвоичного основания несколько уменьшает точность вычислений (при заданном числе разрядов мантиссы), но позволяет увеличить диапазон представляемых в машине чисел и ускорить выполнение некоторых операций, в частности
нормализации, за счет того, что сдвиг может производиться сразу на несколько двоичных разрядов (на четыре разряда для s = 16). Кроме того, уменьшается вероятность появления ненормализованных чисел в ходе вычислений.
Диапазон представимых в машине чисел с плавающей запятой зависит от основания системы счисления и числа разрядов, выделенных для изображения порядка. Точность вычислений при плавающей запятой определяется числом разрядов мантиссы. С увеличением числа разрядов мантиссы увеличивается точность вычислений, но увеличивается и время выполнения арифметических операций.
Задачи, решаемые на ЭВМ, предъявляют различные требования к точности вычислений. Поэтому во многих машинах используется несколько форматов с плавающей запятой с различным числом разрядов мантиссы.
Прямой, обратный и дополнительный коды
В компьютерах с целью упрощения арифметических операций применяют специальные коды для представления чисел. При помощи этих кодов упрощается определение знака результата операции, операция вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению их кодов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства компьютеров, выполняющие арифметические операции.
Для представления отрицательных чисел в компьютерах применяют прямой, обратный и дополнительный коды. Положительные числа представляются в прямом коде. Во всех этих кодах выделяются цифровые разряды и знаковый (крайний слева), представляющий знак числа, причем знак плюс кодируется цифрой 0, а знак минус цифрой 1.
Прямой код двоичного числа G с (n-1) цифровыми разрядами определяется как
|
Gпр = |
G |
при G 0; |
|
A | G | |
при G 0, |
где А — величина, равная весу знакового разряда. Для дробных чисел А = 1,а для целых А = 2n-1.
Сложение в прямом коде чисел, имеющих одинаковые знаки, выполняется достаточно просто. Числа складываются, и сумме присваивается код знака слагаемых. Значительно более сложной является операция алгебраического сложения в прямом коде чисел с различными знаками. В этом случае приходится определять большое по модулю число, производить вычитание чисел и присваивать разности знак большего по модулю числа.
Операция вычитания (алгебраического сложения) сводится к операции простого арифметического сложения при помощи обратного и
дополнительного кодов, используемых для представления отрицательных чисел в машине.
Чтобы представить двоичное отрицательное число в обратном коде, нужно поставить в знаковый разряд 1, а во всех других разрядах заменить 1 нулями, а нули единицами.
Обратный код, если рассматривать его как число, является дополнением модуля исходного числа до наибольшего числа без знака, помещающегося в
разрядную сетку. Для n-разрядной сетки имеем
Go6p=2-2 –(n-1) – lG—l,
если G— — двоичная дробь, и
G—обр = 2n – 1 — |G—|
если G— — целое двоичное число.
При представлении отрицательного двоичного числа в дополнительном коде ставят 1 в разряд знака, а цифровую часть числа заменяют дополнением модуля числа до 1 или 2n-1 соответственно для дробей и целых чисел. Дополнительный код отрицательного числа G определяется
выражением
G— доп=2-|G—|
если G— — двоичная дробь, и
G— доп=2n-|G—|
если G— — целое двоичное число.
Обратный и дополнительный коды числа можно рассматривать как двоичные числа без знаков, при этом для двоичных дробей G—доп = G—обр + 2-(n- 1), а для двоичных целых чисел С—доп=С—обр+1.
Таким образом, дополнительный код числа может быть получен из обратного путем прибавления 1 к младшему разряду обратного кода.
При выполнении расчетов на машине могут возникнуть как «положительный», так и «отрицательный» 0. Положительный 0 в прямом коде имеет вид
(+0)пр= 000… 0.
Отрицательный 0 изображается в прямом коде
( — 0)пр= 100. ..О,
в обратном
(-0)обр= 111…1;
в дополнительном коде отрицательный 0 отсутствует.
При представлении положительных чисел прямым кодом, а отрицательных дополнительным нуль имеет единственное изображение. При применении обратного кода «положительный» и «отрицательный» 0 имеют разные изображения.
Изменению знака отрицательного числа соответствует инвертирование его кода, если число представлено в обратном коде, и инвертирование и
добавление 1 младшего разряда, если отрицательное число представлено в дополнительном коде. В результате получается прямой код соответствующего положительного числа. Сказанное следует из соотношений:
для дробей
-G—пр = |G—| = 2 – 2-(n-1) – G—обр -G—пр = |G—| = 2 – G—доп
для целых чисел
-G—пр = |G—| = 2n – 1 – G—обр -G—пр = |G—| = 2n – G—доп
Рассмотрим применение обратного и дополнительного кодов при алгебраическом сложении n-разрядных двоичных чисел G и Q, когда одно из них или оба числа отрицательны. Могут быть сформулированы следующие правила (предполагаем, что модуль алгебраической суммы меньше 1 для дробей и меньше 2n-1 для целых чисел, и, следовательно, код суммы представим в n-разрядной сетке).
При алгебраическом сложении двух двоичных чисел с использованием обратного (или дополнительного) кода положительные слагаемые представляются в прямом коде, а отрицательные — в обратном (дополнительном) и производится арифметическое суммирование этих кодов, включая разряды знаков, .которые при этом рассматриваются как старшие разряды. При возникновении переноса из разряда знака единица переноса прибавляется к младшему разряду суммы кодов при использовании обратного кода и отбрасывается при использовании дополнительного кода. В результате получается алгебраическая сумма в прямом коде, если эта сумма положительна, и в обратном (дополнительном), если она отрицательна.
Пример.
Пусть требуется выполнить две операции: 176154 и 176215
В первом случае результат будет положительный, а во втором – отрицательный. Переведем эти числа в двоичный код, например, через
|
восьмеричную систему. |
|||||||||
|
176 |
8 |
154 |
8 |
215 |
8 |
||||
|
176 |
22 |
8 |
152 |
19 |
8 |
208 |
26 |
8 |
|
|
0 |
16 |
2 |
2 |
16 |
2 |
7 |
24 |
3 |
|
|
6 |
3 |
2 |
|||||||
|
17610=2608 |
15410=2328 |
21510=3278 |
0101100002 0100110102 0110101112
инвертируем вычитаемые в обратный и дополнительный коды
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Машинные коды двоичного числа
В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. При помощи этих кодов упрощается определение знака результата операции. Операция вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению кодов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства ЭВМ, выполняющие арифметические операции.
Для представления чисел со знаком в ЭВМ применяют прямой, обратный и дополнительный коды.
Общая идея построения кодов такова. Код трактуется как число без знака, а диапазон представляемых кодами чисел без знака разбивается на два поддиапазона. Один из них представляет положительные числа, другой – отрицательные. Разбиение выполняется таким образом, чтобы принадлежность к поддиапазону определялась максимально просто.
Наиболее распространенным и удобным является формирование кодов таким образом, чтобы значение старшего разряда указывало на знак представляемых чисел, т.е. использование такого кодирования позволяет говорить о старшем разряде как о знаковом (бит знака) и об остальных как о цифровых разрядах кода.
Прямой код
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль для положительных чисел или единица для отрицательных чисел) перед его старшим числовым разрядом.
Цифровые разряды прямого кода содержат модуль представляемого числа, что обеспечивает наглядность представления чисел в прямом коде (ПК).
Пример. Записать прямой код чисел 
Рекомендуемые материалы
Решение: Рассмотрим однобайтовое представление двоичного числа.

В прямом коде нуль имеет двоякое изображение: 

В общем случае ОК является дополнением модуля исходного числа до наибольшего числа без знака, помещенного в разрядную сетку.
Обратный код
В обратном коде (ОК), также как и в прямом коде, для обозначения знака положительного числа используется бит, равный нулю, и знака отрицательного – единице.
Обратный код положительного двоичного числа совпадает с его прямым кодом. Обратный код отрицательного двоичного числа содержит единицу в знаковом разряде, формируется дополнением модуля исходного числа нулями до самого старшего разряда модуля, а затем поразрядной заменой всех нулей числа на единицу и всех единиц на нули. Обратный перевод осуществляется в той же последовательности.
Пример. Записать обратный код чисел 
Решение:



Работа с обратным кодом вызывает ряд трудностей. В частности, возникают два нуля: положительный и отрицательный, т.е. в прямом коде (в котором представлены положительные числа) имеет место 

Дополнительный код
Дополнительный код (ДК) строится следующим образом.
Дополнительный код положительного двоичного числа совпадает с его прямым кодом. Для отрицательных двоичных чисел сначала формируется обратный код (ОК), а затем к младшему разряду (МЗР) прибавляют 1. Обратный перевод ДК в ПК осуществляется аналогичными операциями в той же последовательности.
Пример. Записать дополнительный код чисел 
Решение:



Использование ДК для представления отрицательных чисел устраняет двусмысленное представление нулевого результата (возникновение двух нулей: положительного и отрицательного), так как отрицательный ноль исчезает.
В общем случае использованием ДК для записи отрицательных чисел можно перекрыть диапазон десятичных чисел от –2k-1 до +2k-1-1, где k – число используемых двоичных разрядов, включая знаковый. Так, с помощью одного байта можно представить десятичные числа от 

В ЭВМ используется быстрый способ формирования ДК. Его суть заключается в следующем. Двоичное число в ПК просматривается от младшего значащего разряда к старшему. Пока встречаются нули, их копируют в одноименные разряды результата. Первая встретившаяся единица также копируется в соответствующий разряд, а каждый последующий бит исходного числа заменяется на противоположный (0 – на 1, 1 – на 0).
Пример. Записать дополнительный код числа 
Решение:
1 способ (быстрый).

2 способ.

Как видно, результаты, полученные при преобразовании обоими методами, совпадают.
Модифицированные обратные и дополнительные коды
Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак «+» в этих кодах обозначается двумя нулевыми разрядами, а «–» – двумя единичными разрядами. Целью введения модифицированных кодов являются фиксация и обнаружение случаев переполнения разрядной сетки. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов «01» свидетельствует о положительном переполнении разрядной сетки, а «10» — об отрицательном переполнении.
Лекция «6. Информационный рынок» также может быть Вам полезна.
Вопросы для самопроверки:
1. Дайте определение системы счисления. Какие системы счисления Вы знаете?
2. Сформулируйте правило перевода целых чисел из одной системы счисления в другую.
3. Сформулируйте правило перевода дробных чисел из одной системы счисления в другую.
4. В чем особенность перевода чисел из восьмеричной (шестнадцатеричной) системы счисления в двоичную и наоборот?
5. Сформулируйте правило формирования прямого, обратного и дополнительного кодов двоичного числа.