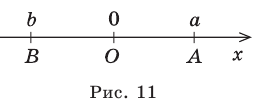
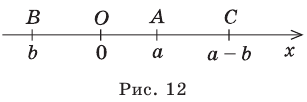
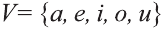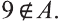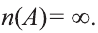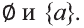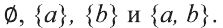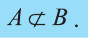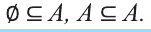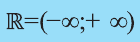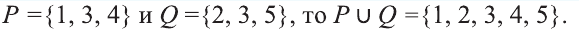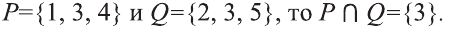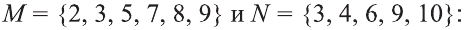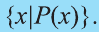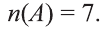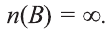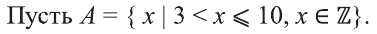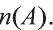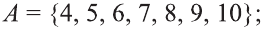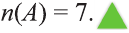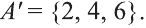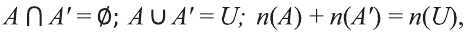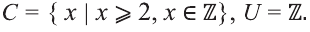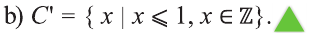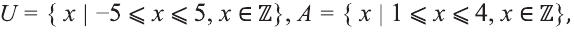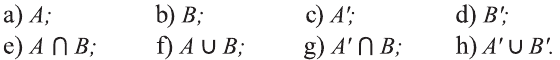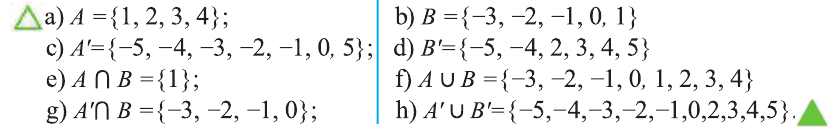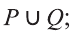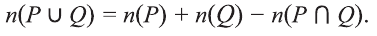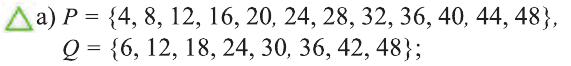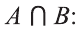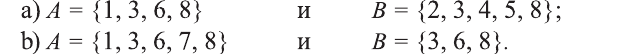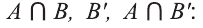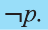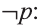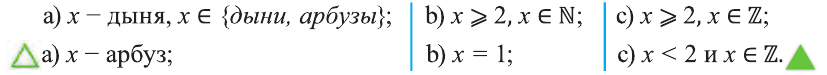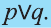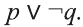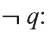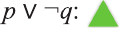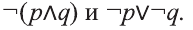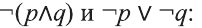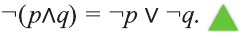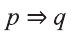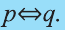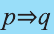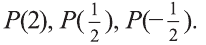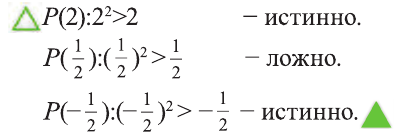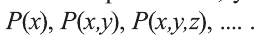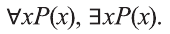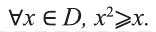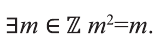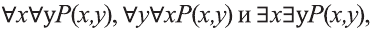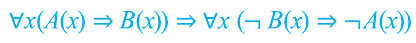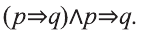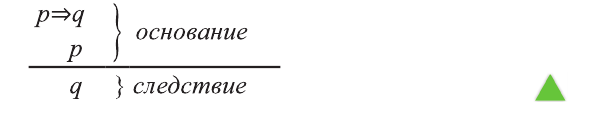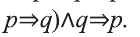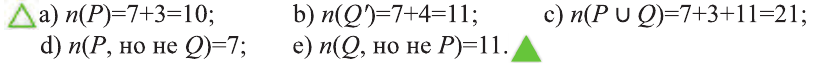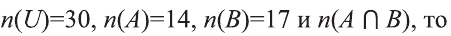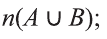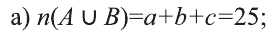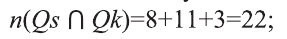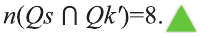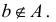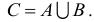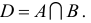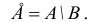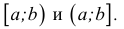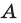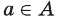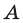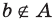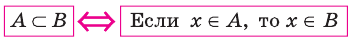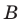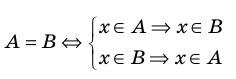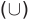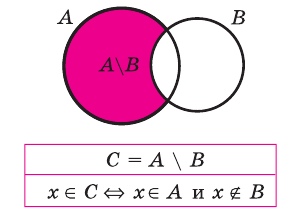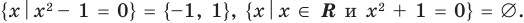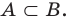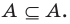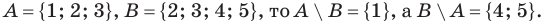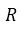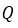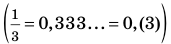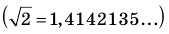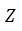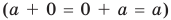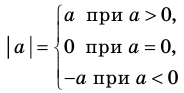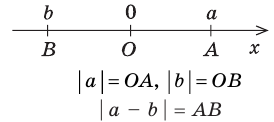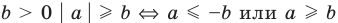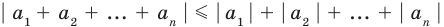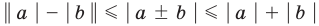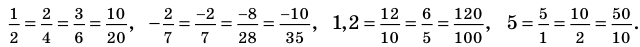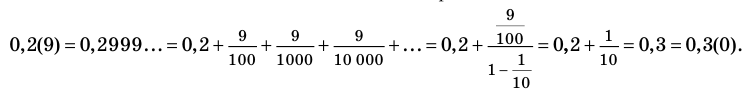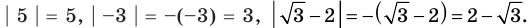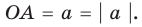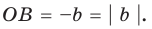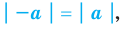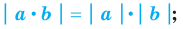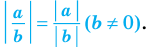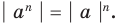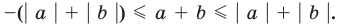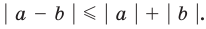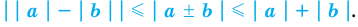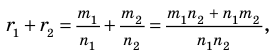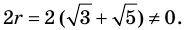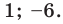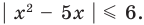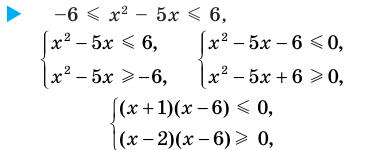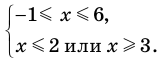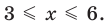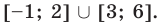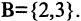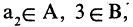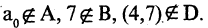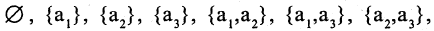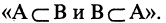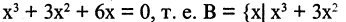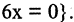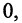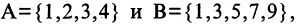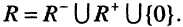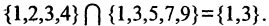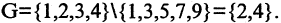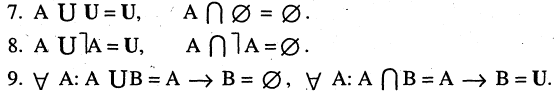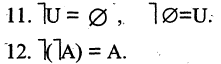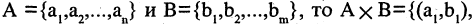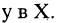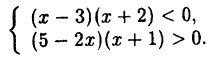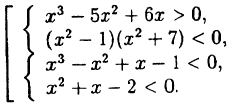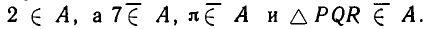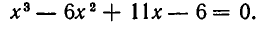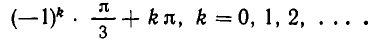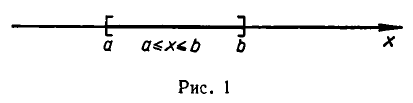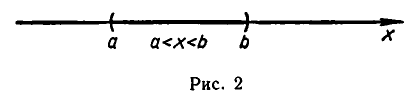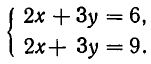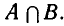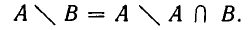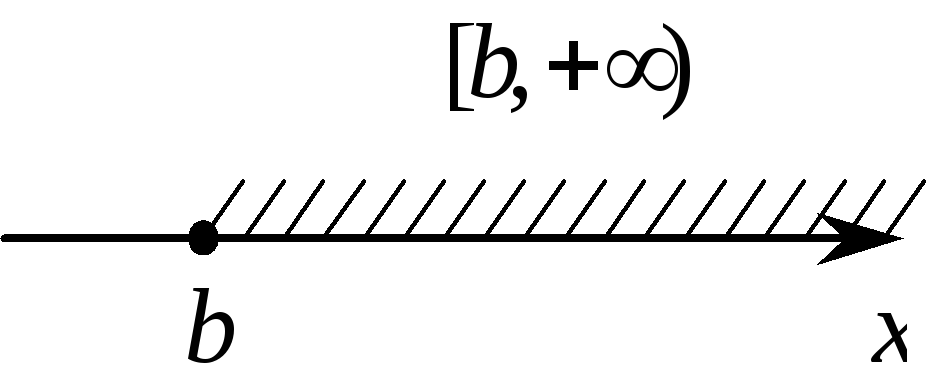Содержание:
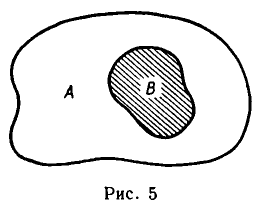
Множества
Понятие множества является одним из исходных понятий математики в том смысле, что его нельзя определить с помощью более простых, чем оно само, понятий. В повседневной жизни часто приходится рассматривать набор некоторых объектов как единое целое. Скажем, когда биолог изучает флору и фауну некоторой местности, он делит организмы на виды, а виды на семейства. При этом каждый вид рассматривается как единое целое, состоящее из организмов.
Множество может состоять из объектов различной природы. Например, вес реки Азии или все слова в словаре могут рассматриваться как множества.
Знаменитый немецкий математик Г. Кантор (1845 -1918) дал следующую описательную формулировку: «Множество есть совокупность, мыслимая как единое целое».
Объекты, составляющие множество, называются его элементами.
Обычно, для удобства, множество обозначается заглавными буквами латинского алфавита, например, А, В, С,…, а его элементы — прописными.
Множество А, состоящее из элементов а, b, с, … , будем записывать в виде A = {а, b, с,…}. Отметим, что записи {6, 11} , {11, 6} , {11, 6, 6, 11} означают одно и то же множество.
При ведем примеры множеств. Например, множество {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} — множество цифр десятичной системы счисления ,
То, что х является элементом множества А, будем обозначать как 
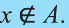
Например, для множества 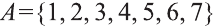

Если число элементов, составляющих множество, конечно, то такое множество будем называть конечным, в противном случае бесконечным. Например, множество 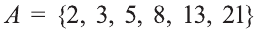
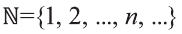
В качестве еще одного примера бесконечного множества можно привести множество всех натуральных чисел, не меньших 13.
Обозначим через 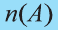
в силу того, что число всех его элементов равно 6. Множество, не содержащее ни одного элемента, называется пустым и обозначается так: 0
Пустое множество 0 считается конечным и для него я(0)= 0.
Для бесконечного множества А принято, что
Если вес элементы множества А также принадлежат множеству В, то говорят, что множество А — подмножество множества В и обозначают так: 
Во множестве {а} лежат два подмножества:
Множество {а, b} имеет четыре подмножества:
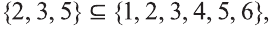
Если множество А имеет элементы, не принадлежащие В, то множество А не может быть подмножеством В. Этот факт мы будем записывать так:
Например, пусть А={ 1, 2, 3, 4}, В={2, 3, 4, 5}. Так как 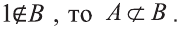
Если 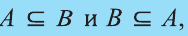
Например, множество всех правильных треугольников совпадает со множеством всевозможных треугольников, у которых все углы равны. Причина этого заключается в том, что у любого правильного треугольника
все углы равны, и, наоборот, если у треугольника все углы равны, то он является правильным.
Напомним основные числовые множества: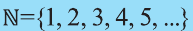
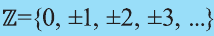
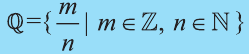
Множество действительных чисел
Объединение и пересечение множеств
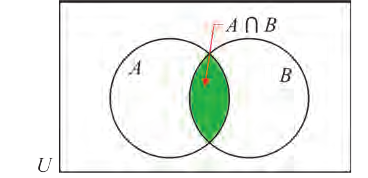
1) Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А, В, называется объединением множеств.
Объединение множеств А, В обозначается через
Например, если
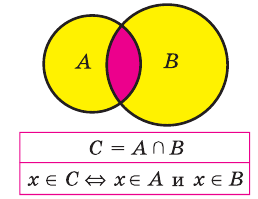
2) Множество, состоящее из элементов, принадлежащих обоим множествам А, В, называется пересечением множеств. Пересечение множеств А. В обозначается через
Например, если
Множества, не имеющие общих элементов, называются не пересекающимися.
Пример:
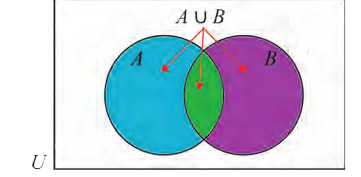
Для множеств
a) определите, какие из утверждений верны, а какие неверны:
b) найдите множества:
c) определите, какие из утверждений верны, а какие неверны:
Решение:
а) Так как число 4 не является элементом множества М, то утверждение 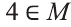
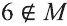
b). 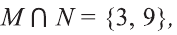
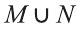
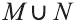
c) Утверждение 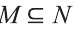
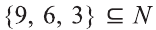
В некоторых случаях для задания множества указывается характеристическое свойство, истинное для всех элементов множества и ложное для остальных. Если мы кратко запишем тот факт, что элемент х удовлетворяет свойству Р как Р(х), то множество всех элементов, удовлетворяющих свойству Р обозначается так:
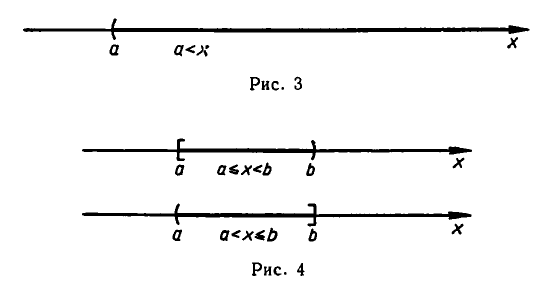
Например, запись 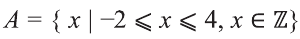
На числовом луче это множество изображается так:
Видно, что 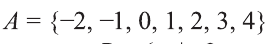
Аналогично запись 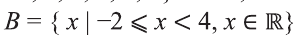
На числовом луче это множество изображается так:
Видно, что, 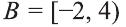
Пример:
a) Как читается эта запись?
b) Выпишите последовательно элементы этого множества.
c) Найдите
Решение:
a) «Множество всех целых чисел, больших 3 и меньших или равных 10»;
b).
c).
Рассмотрим множество всех натуральных чисел, больших или равных 1, но меньших или равных 8. Пусть нас интересуют только его подмножества.
В таком случае, обычно вводится множество 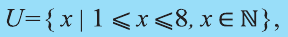
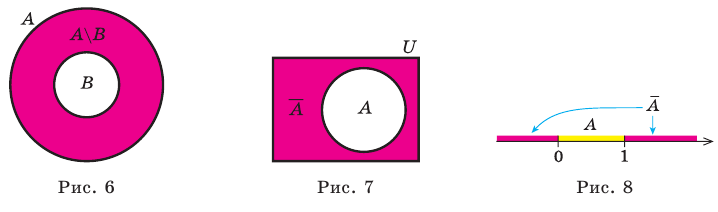
Множество А содержащее все элементы универсального множества U, не являющиеся элементами множества А, называется дополнением множества А.
Например, если 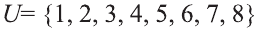
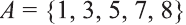
Очевидно, что
т.е. множества А и А’ не имеют общих элементов, а также вес составляющие их элементы образуют в совокупности универсальное множество U.
Пример:
Пусть U универсальное множество. Найдите С’, если:
а) С = {все четные числа); b).
Решение:
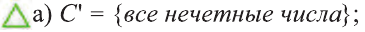
Пример:
Пусть
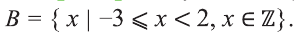
Решение:
Пример:
Пусть 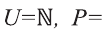
b) найдите 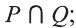
d) проверьте выполнение равенства
Решение:
Значит, 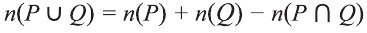
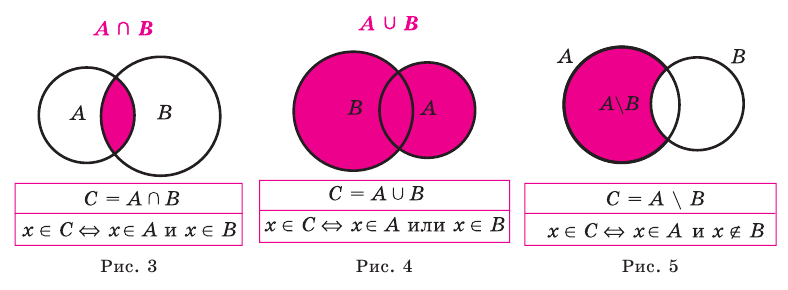
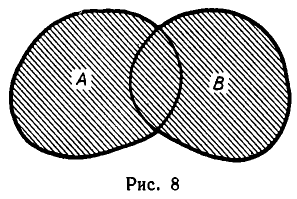
Диаграммы Венна
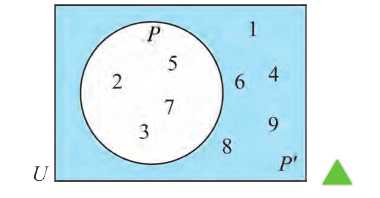
Например, на этом рисунке изображено множество А, лежащее внутри универсального множества 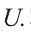
Если 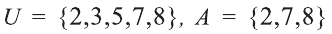
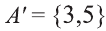
Мы знаем, что если 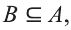
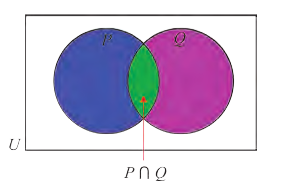
Все элементы пересечения 
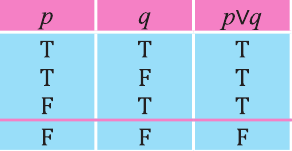
Все элементы объединения A U В принадлежат либо А, либо В, либо обоим одновременно. Значит, на соответствующей диаграмме Венна область, соответствующая множеству A U В, изображается следующим образом:
Пример:
Пусть 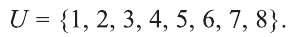
Венна множества:
Решение:
Удобно на диаграмме Венна множества раскрашивать.
Например, на рисунке раскрашены множества А,
Высказывание
Высказывание — это повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Вопросительные предложения, повествовательные предложения, описывающие личное отношение субъекта, например «Зеленый цвет приятен», не являются высказываниями. Отметим, что существуют высказывания, истинность или ложность которых не определяются однозначно.
Например, высказывание «Этот писатель родился в Ташкенте» может быть истинным по отношению к некоторым писателям и ложным по отношению к другим.
Пример:
Укажите, какие из предложений являются высказываниями. В случае, когда предложение является высказыванием, однозначно ли определяется его истинность — ложность?
а) 20:4=80; b) 25-8=200;
с) Где мой карандаш? d) У тебя глаза голубые.
Решение:
a) Это высказывание и оно ложно, так как 20:4=5;
b) это высказывание и оно истинно;
c) это вопросительное предложение и поэтому оно не является высказыванием;
d) это высказывание. Истинность-ложность его определяется неоднозначно, так как применительно к некоторым людям оно истинно, а к другим — ложно.
Мы будем обозначать высказывания буквами p,q,r … .
Например, р: во вторник прошел дождь; q: 20:4=5; r: х — четное число. Для построения нескольких сложных высказываний служат символы, называемые логическими связками: 


Рассмотрим их подробней.
Отрицание
Для высказывания р высказывание вида «не р» или «неверно, что р» называется отрицанием высказывания р и обозначается как
Например,
отрицанием высказывания
р: Во вторник шел дождь
является высказывание
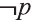
Отрицанием высказывания
р: У Мадины глаза голубые
является высказывание
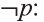
Ясно, что если р истинно, то 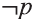
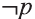
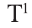
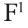
1 Буквы Т и F — начальные буквы английских слов «true» (истинно) и «false» (ложно) соответственно.
Пример:
Составьте отрицание высказывания:
Решение:
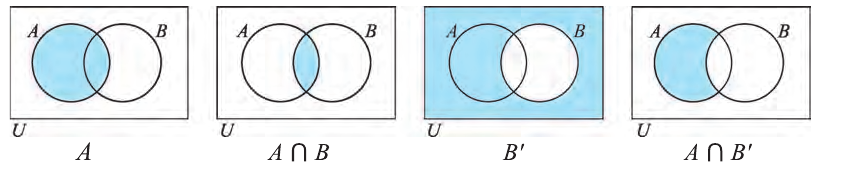
Удобно находить отрицание высказывания с помощью диаграмм Венна. Например, рассмотрим высказывание:
р: «Число х больше, чем 10 «.
На диаграмме U — множество всех чисел, множество Р — множество истинности высказывания р, то есть множество всех х , для которых это высказывание истинно. Множество Р’ является множеством истинности отрицания 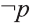
Пример:
На множестве 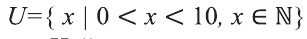
Решение:
Пусть множество Р — множество истинности высказывания р, а множество Р’ — множество высказывания 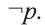
Конъюнкция
Высказывание, образованное из двух высказываний с помощью связки «и», называется конъюнкцией заданных высказываний.
Конъюнкция высказываний р, q обозначается через
Например, конъюнкция высказываний,
р: Эльдар на завтрак ел плов;
q: Эльдар на завтрак ел самсу.
имеет вид:
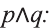
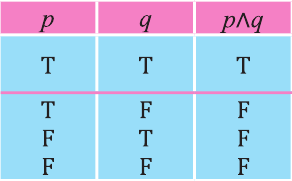
Видно, что высказывание 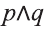
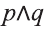
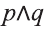
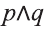
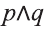
Первый и второй столбцы таблицы составлены из всех возможных значений истинности высказываний р, q.
На диаграмме Р — множество истинности высказывания р, Q — множество истинности высказывания q , а множество истинности высказывания 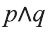
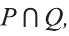
Дизъюнкция
Высказывание, образованное из двух высказываний с помощью связки «или», называется дизъюнкцией заданных высказываний.
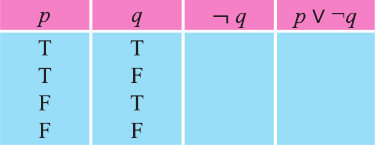
Дизъюнкция высказываний р, q обозначается через
Например, дизъюнкция высказываний,
р: Эльдар сегодня посетит библиотеку,
q: Эльдар сегодня посетит театр .
имеет вид:
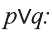
Высказывание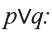
Высказывание 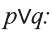
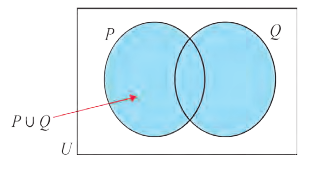
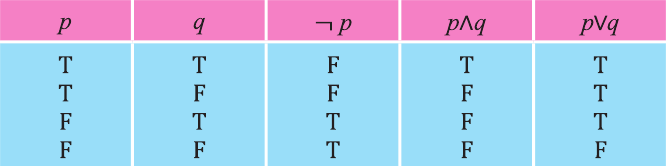
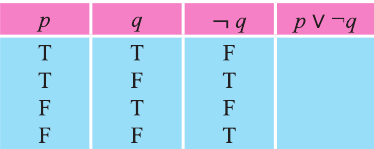
Дизъюнкция имеет следующую таблицу истинности:
pVq истинно, когда хотя бы одно из высказываний р, q истинно.
pVq ложно, когда оба высказывания p, q ложны.
На диаграмме Р — множество истинности высказывания р, Q — множество истинности высказывания q, а множество истинности высказывания pVq является множество 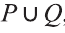
Логическая равносильность
Составим, используя буквы и символы логических связок таких, как отрицание, конъюнкция и дизъюнкция, символическую запись более сложных высказываний естественного языка, при этом не обращая внимания на их истинность или ложность.
Объединяя таблицы истинности для отрицания, конъюнкции и дизъюнкции, можно составить таблицы истинности для более сложных высказываний:
Пример 1. Составьте таблицу истинности высказывания
1 шаг.
Выпишем таблицу и заполним сначала первый и второй столбец всеми возможными значениями истинности р и q:
2 шаг. Учитывая значения истинности q, заполним третий столбец значениями истинности
3 шаг Учитывая значения истинности p и 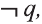
Высказывание, являющееся истинным всегда, называется законом логики или тавтологией.
То, что высказывание является законом логики, можно доказать при помощи таблицы истинности.
Пример:
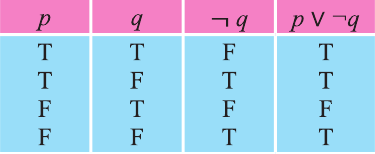
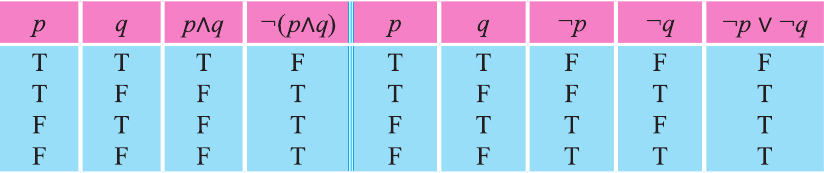
Докажите, что высказывание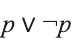
Заполним таблицу истинности:
Решение:
Видно, что высказывание 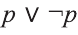
Если для двух высказываний соответствующие их значениям истинности столбцы одинаковы, то эти высказывания называются логически равносильными.
Пример:
Докажите, что следующие высказывания являются логически равносильными
Решение:
Составим таблицы истинности для высказываний
Так как у высказываний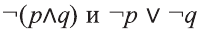
Мы будем обозначать этот факт так:
Импликация
Высказывание, образуемое из двух высказываний с помощью связки «если …., то …» называется импликацией этих двух высказываний.
Импликация «Если р, то q» обозначается как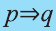
При этом высказывание р называется достаточным условием для q, а высказывание q — необходимым условием для р.
высказывание q — необходимым условием для р.
Рассмотрим , например, высказывания
р: У Сардора есть телевизор; q: Сардор будет смотреть кино.
Тогда высказывание 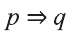
Если у Сардора есть телевизор, то он будет смотреть кино.
Точно также
Для того, чтобы Сардор смотрел кино достаточно, чтобы у него был телевизор.
Можно заметить, что высказывание 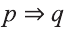
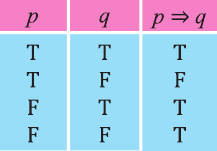
Пример:
Рассмотрим высказывания
р: «Анора часто смотрит кинофильмы»;
q: «Барно часто смотрит кинофильмы
r: «Барно не сдаст экзамен»;
s: «произойдет чудо».
Имеем: 1. 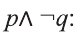
2. 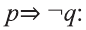
3. 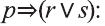
4. 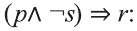
5. 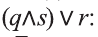
Эквиваленция
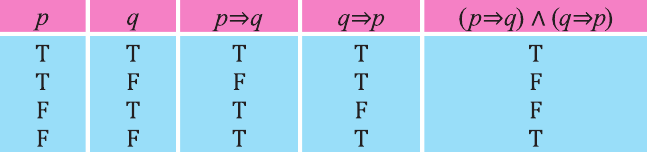
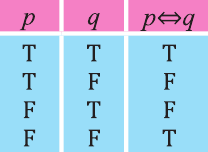
Высказывание вида 
Запись 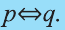
Пример:
р: х — четно, q: последняя цифра числа х четна. Выразите высказывание
Решение:
Рассмотрим высказывание,

Тогда запись 

Видно, что высказывание 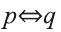
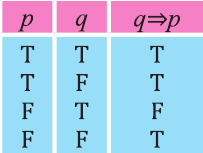
Конверсия
Конверсией высказывания 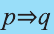
Конверсия имеет следующую таблицу истинности:
Пример:
Рассмотрим высказывания
р: треугольник равнобедренный,
q: два угла треугольника равны.
Выразите на естественном языке высказывание 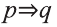
Решение:
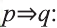
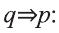
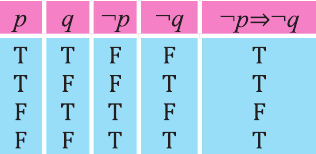
Инверсия
Инверсией высказывания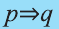
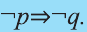
Эта таблица совпадает с таблицей истинности высказывания 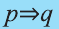
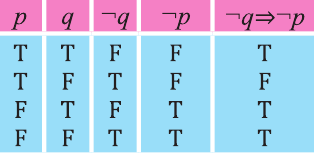
Контрапозиция
Контрапозицией высказывания 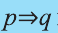

Эта таблица совпадает с таблицей истинности высказывания 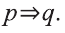
Пример:
Рассмотрим высказывание. Все учителя живут поблизости от школы». Составим его контрапозицию.
Решение:
Данное высказывание можно сформулировать так: «Если этот человек — учитель, что он живет поблизости от школы».
Это предложение имеет форму 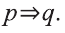
р: этот человек — учитель,
q: этот человек живет поблизости от школы.
Контрапозиция 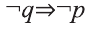
«Если этот человек не живет поблизости от школы, то он не является учителем.
Пример:
Рассмотрим высказывания:
р: Самандар находится в библиотеке, q: Самандар читает книгу.
Составьте имликацию, конверсию, инверсию и контрапозицию
Решение:
Отметим, что импликация и конверсия логически не равносильны, так как , например , Самандар может читать книгу и в классе.
Предикаты и кванторы
В некоторых предложениях участвуют переменные, при этом подставив вместо них конкретные значения, получим высказывания. Такие предложения называются предикатами.
Пример:
Пусть задан предикат 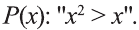
Решение:
В некоторых предикатах переменную можно определить исходя из контекста.
Например, в предложениях «Этот писатель родился в Ташкенте» и «Он родился в Ташкенте» переменными являются словосочетание». «Этот писатель» и местоимение «он» соответственно. Если вместо переменной подставить значение «Абдулла Кадыри», получим истинное высказывание «Абдулла Кадыри родился в Ташкенте». Если вместо переменной подставить значение «Шекспир», получим ложное высказывание «Шекспир родился в Ташкенте».
Обозначив переменную через х, вышеуказанные предложения можно записать в виде «х родился в Ташкенте».
В предикате могут участвовать одно или несколько переменных. В зависимости от количества переменных, участвующих в предикате, будем обозначать его так:
Используя совместно с предикатом специальные символы 
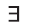
Например, новое высказывание вида 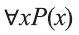
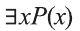
К примеру, рассмотрим предикат Р(х): «х родился в Самарканде». Тогда высказывание 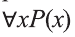
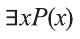
Приведем примеры, в которых можно определить истинность-ложность высказываний вида
Пример:
Пусть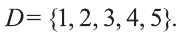
Решение:
Проверим:
Значит, высказывание, 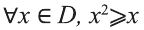
Следует отметить, что для того, чтобы доказать ложность высказывания 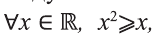
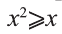
Действительно, при
Любое значениех, которое показывает, что высказывание 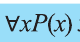
Пример:
Докажите истинность высказывания
Решение:
Так как 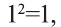
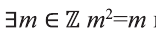
Если же 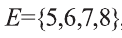
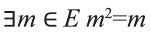
Приведем два важных закона логики, связанных с операцией отрицания:
Для понимания смысла этих законов приведем пример.
Если запись 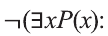
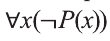
не существует отличников», тогда запись означает логически равносильное ему утверждение «Все мои одноклассники не являются отличниками».
Точно также, формула 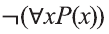
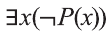
Очевидно, что с помощью кванторов и предиката 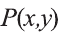
из которых, в свою очередь, можно построить всказывания вида:
В то время, когда смысл высказываний
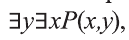
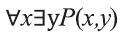
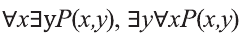
Рассмотрим, например, предикат Р(х,у): человек у — отец моего одноклассника х.
В этом случае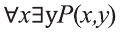
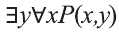
Аналогично можно показать, что высказывания,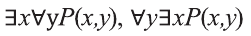
С помощью кванторов и предикатов можно построить и другие законы логики. Например, высказывание «Если все вороны черные, то ни одна не черная птица не является вороной «, служит примером закона логики вида:
Законы правильного мышления (аргументации)
В процессе познания действительности мы приобретаем новые знания. Некоторые из них непосредственно, в результате воздействия предметов внешнего мира на органы чувств. Но большую часть знаний мы получаем пу тем выведения новых знаний из знаний уже имеющихся. Чтобы научиться стройно и последовательно излагать свои мысли, правильно делать выводы, необходимо пользоваться законами логики. Определенность, непротиворечивость, последовательность и обоснованность являются обязательными качествами правильного мышления. Законы логики устанавливают необходимые связи в последовательном ряду мыслей и умозаключений.
Суждение представляет собой форму мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах или отношениях. Например, в суждении «Железо-металл» утверждается связь между предметом (железо) и его признаком (являться металлом). В суждении «Яйцо появилось раньше курицы » утверждается связь между двумя предметами (яйцо и курица). Так как суждение выражается в форме повествовательного предложения, причем суждение может быть либо истинным, либо ложным, то каждое суждение имеет форму высказывания.
Умозаключение- это такая форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам получается некоторое суждение, называемое заключением или выводом.
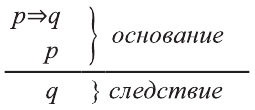
Пусть S-совокупность исходных суждений (посылок), Р- заключение. В этом случае, умозаключение имеет логическую форму вида 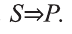
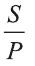
Если Собир занимается спортом, то будет здоров. Собир занимается спортом. Следовательно, Собир будет здоров.
Найдем логическую форму этого умозаключения.
Пусть р: Собир занимается спортом; q: Собир будет здоров. Тогда умозаключение имеет вид:
Так следствие вытекает из суждений 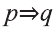
Составим соответствующую таблицу истинности:
Получили тавтологию. Это показывает правильность умозаключения, то есть мы из данного основания получили правильное следствие.
Пример:
Покажите неправильность умозаключения:
Если треугольник имеет три стороны, то 2+4-7.
Следовательно, треугольник имеет три стороны.
Решение:
Найдем логическую форму этого умозаключения.
р: треугольник имеет три стороны.
q: 2+4=7
Имеем:
Так как здесь 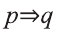
Составим соответствующую таблицу истинности:
В результате мы не получили тавтологию. Это показывает неверность умозаключения, то есть мы из данного основания не получили правильное следствие.
Ниже мы приведем некоторые правила правильных умозаключений:
Доказательство верности вышеуказанных умозаключений мы оставляем учащимся в качестве упражнения.
Софизмы и парадоксы
Одним из первых соответствующие примеры привел математик Зенон, живший в 5 веке до нашей эры в Древней Греции. Например, Зенон «доказал», что быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения она находится впереди Ахиллеса. Приведем его рассуждения. Допустим, Ахиллес бежит в 10 раз быстрее, чем черепаха, и находи тся позади нее на расстоянии в 100 шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползет 10 шагов.
За то время, за которое Ахиллес пробежит 10 шагов, черепаха проползет еще 1 шаг, и так далее. Процесс будет длиться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Примеры Зенона связаны с понятиями бесконечности и движения, которые имели большое значение в развитии физики и математики.
Некоторые софизмы обсуждали в переписке между собой наши великие соотечественники Беруни и Ибн Сино, а также они встречаются в произведениях Фараби.
Приведем простейшие примеры на софизмы и обсудим их.
Пример:
Куда пропали 1000 руб? Три друга отобедали в кафе, после чего официант дал им счет на 25000 руб. Каждый из трех друзей достал по купюре в 10000 руб, в итоге они отдали официанту 30000 руб. На сдачу официант отдал 5000 руб более мелкими купюрами. Друзья взяли по 1000 руб себе, а оставшиеся 2000 руб отдали другу на такси. Один из друзей стал рассуждать: «Каждый из нас потратил по 9000 руб, что в итоге составляет 27000 руб. Затем 2000 руб отдали на такси, значит, в итоге получается 29000 руб. Куда пропали 1000 руб?»
Решение:
Основной «подвох» в этом рассуждении заключается в том, что 2 От древнегреческого уловка.
расчеты сделаны неверно. Действительно, трое друзей сложились по 9000 руб и получили 27000 руб. Из этих денег 25000 руб заплатили за обед, а 2000 руб заплатили за такси. Следовательно, общая трата составила 27000 руб. Тс 2000 руб находятся внутри 27000 руб.
Пример:
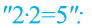
2(10—8—2)=25—20—5
2-2-(5—4—1)=5-(5—4—1)
Сократим левую и правую часть последнего равенства на общий делитель (5-4-1). В итоге получим равенство 2-2=5.
Основной «подвох» в этом рассуждении заключается в том, что мы поделили обе части равенства 2-2-(5-4-1)=5-(5-4-1) на нуль.

Парадоксы, обычно, возникают в теориях, логические основы которых не определены полно.
Пример:
Парадокс лжеца. Рассмотрим высказывание «То, что я утверждаю сейчас — ложь».
Если это высказывание истинно, значит, исходя из его содержания, верно то, что данное высказывание -ложь. Но если оно -ложь, тогда неверно то, что оно утверждает, то есть утверждение о ложности данного высказывания неверно, значит, данное высказывание истинно. Таким образом, цепочка рассуждений возвращается в начало.
Пример:
Прилагательное русского языка назовем рефлексивным, если оно обладает свойством, которое определяет.
Например, прилагательное «русский» — рефлексивное, а прилагательное «английский» — нерефлексивное, прилагательное «трехсложный» — рефлексивное (это слово состоит из трех слогов), а прилагательное «четырехсложный» — нерефлсксивное (состоит из пяти слогов). Вроде бы ничто не мешает нам определить множество {все рефлексивные прилагательные}. Но давайте рассмотрим прилагательное «нерефлексивный». Оно рефлексивное или нет?
Можно заявить, что прилагательное «нерефлексивный» не является ни рефлексивным, ни нерефлексивным. Действительно, если это слово рефлексивное, то по своему смыслу, оно нерефлексивное. Если же это от древнегреческого 
Пример:
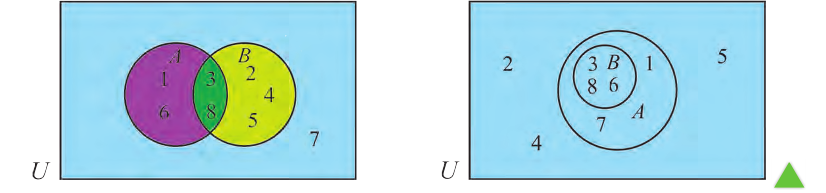
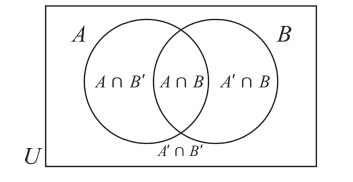
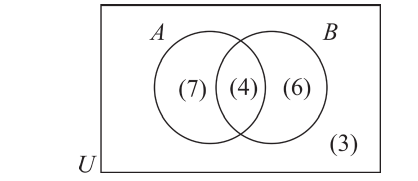
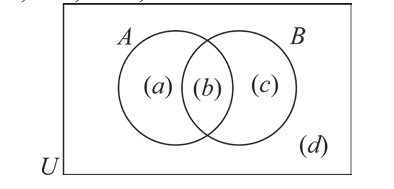
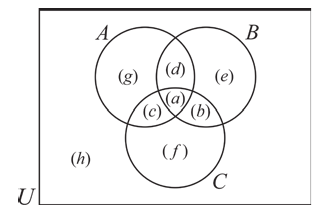
Два взаимно пересекающихся множества А, В делят универсальное множество на четыре части:
Следовательно, число элементов универсального множества является суммой количеств элементов этих частей.
На следующей диаграмме мы заключили известные количества элементов частей универсального множества в круглые скобки:
Здесь, например, обоим множествам А, В принадлежат 4 элемента, а 3 элемента не принадлежат ни одному из них.
Так как произвольный элемент множества U, принадлежит только одному из этих 4 частей , то число элементов множества U равно 7+4+6+3=20.
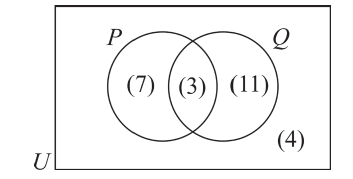
Пример:
Используя рисунок, найдите число элементов следующих множеств:
d). Множество элементов, принадлежащих Р, но не принадлежащих Q
е) Множество элементов, принадлежащих Q, но не принадлежащих Р;
f) Множество элементов, не принадлежащих ни Р, ни Q.
Пример:
Если
a) Найдите
b) Сколько элементов содержит множество элементов, принадлежащих А, но не принадлежащих В‘?
Решение:
Составим диаграмму Венна:
Из того, что 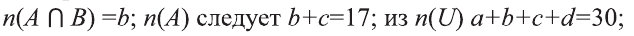
Из диаграммы получаем следующее:
b) Число элементов, принадлежащих А, но не принадлежащих В, равно а= 8
Пример:
Из 27 учеников, посещающих спортивную секцию, 19 имеют темные волосы, 14 — черные глаза, а 11 имеют и темные волосы и черные глаза одновременно.
a) Изобразите эту информацию с помощью диаграммы Венна. Объясните ситуацию.
b) Найдите число учеников, которые I имеют или темные волосы или черные глаза; II темноволосых, но не черноглазых?
Решение:
а) Пусть Qs — множество темноволосых, a Qk множество черноглазых учеников.
Изобразим ситуацию на диаграмме:
b) Используя диаграмму, определим следующее:
I количество учеников, имеющих или темные волосы или черные глаза:
II количество темноволосых учеников, не обладающих черными глазами:
Пример:
На футбольном соревновании город представляют три команды А, В и С. 20 процентов населения города болеют за команду И, 24 процента — за В, 28 процентов — за С. 4 процента жителей болеют и за С и за И, 5 процент, жителей болеют и за В и за А, а 6 процентов жителей болеют и за В и за С. Кроме того, 1 процент населения болеет за все три команды.
Сколько процентов жителей:
a) болеют только за команду А;
b) болеют и за А и за В, но не болеют за команду С;
c) не болеют ни за одну из команд?
Решение:
Заполним для начала соответствующую диаграмму Венна.
а= 1, так как 1 процент жителей болеет за все команды.
a+d=4, так как 4 процента жителей болеет и за И и за В.
а+b=6, так как 6 процентов жителей болеют и за В и за С а+с=5, так как 5 процентов жителей болеют
—-
Множества
Понятие множества принадлежит к числу первичных, не определяемых через более простые. Под множеством понимается совокупность некоторых объектов, объединенных по определенному признаку. Объекты, которые образуют множество, называются элементами, или точками, этого множества.
Множества обозначаются прописными буквами, а их элементы — строчными. Если 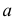
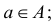
Например, 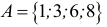
Множество, не содержащее ни одного элемента, называется пустым и обозначается 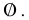
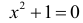
Два множества называются равными, если они состоят из одних и тех же элементов. Например, если 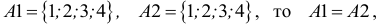
множества равны.
Объединением двух множеств А и В называется множество С, состоящее из элементов, принадлежащих хотя бы одному из данных множеств, т.е.
Пересечением двух множеств А и В называется множество D, состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств А и В, т.е.
Разностью двух множеств А и В называется множество E, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
Пример 1. Даны множества 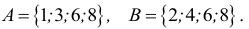
Решение. Объединение двух данных множеств — 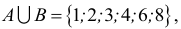
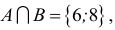
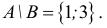
Множества, элементами которых являются действительные числа, называются числовыми.
Обозначения множеств:
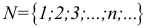
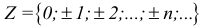
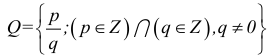
R — множество действительных чисел;
I — множество иррациональных чисел;
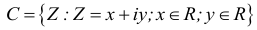
Геометрически, каждому действительному числу соответствует точка числовой оси, и наоборот, каждой точке прямой — определенное действительное число.
Множество X, элементы которого удовлетворяют: неравенству 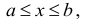
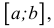
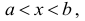
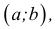
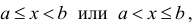
В дальнейшем все указанные множества мы объединяем термином промежуток X.
——
Множества и операции над ними
Под множеством будем понимать совокупность объектов, наделенных определенными свойствами. Эти свойства должны полностью определять данное множество, то есть являться признаками, по которым относительно любого объекта можно решить, принадлежит он данному множеству или нет. Синонимами термина «множество» являются термины «класс «семейство «совокупность». Объекты, из которых состоит данное множество, называют его элементами.
Чаще всего множество обозначают большими буквами латинского или греческого алфавита, а его элементы — малыми буквами. Если a — элемент множества A, то пишут a ∈ A (читают: «a принадлежит множеству A») или A 3 a (множество A содержит элемент a). Запись a ∈/ A означает, что a не является элементом множества A.
Множество обычно записывают одним из следующих способов:
A = {a , . . . , 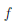
Первая запись означает, что множество A состоит из элементов a, . . . , 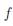
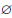
Определение 1.1. Множества A и B называются равными (или совпадающими), если они состоят из одних и тех же элементов, то есть x ∈ A тогда и только тогда, когда x ∈ B .
Коротко это высказывание записывают: A = B, а отрицание этого утверждения — в виде: 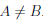
Определение 1.2. Если каждый элемент множества A является элементом множества B , то говорят, что A есть подмножество множества B (или A есть часть B ), и пишут A ⊂ B (читается: «Множество A содержится в множестве B») или B ⊃ A (читается: «Множестоо B содержит множество A»).
Отметим следующие свойства отношения включения:
1. A ⊂ A, то есть всякое множество есть подмножество себя самого;
2. Если A ⊂ B и B ⊂ C, то A ⊂ C (отношение включения транзитивно);
3. Если A ⊂ B и B ⊂ A, то A = B.
Удобно считать, что 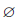
Пусть A и B — некоторые подмножества множества E. Введем наиболее простые операции с множествами.
Определение 1.3. Объединением множеств A и B называется множество, обозначаемое A ∪ B и состоящее из всех элементов, которые принадлежат или множеству A или B .
Таким образом, x ∈ A ∪ B , если x ∈ A, но x 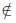
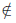
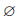
Определение 1.4. Пересечением множеств A и B называют множество, обозначаемое A∩B и состоящее из всех элементов, каждый из которых принадлежит и A и B .
Если множества A и B не имеют общих точек, то A ∩ B =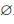
Определение 1.5. Разностью множеств A и B называют множество, обозначаемое A B и состоящее из всех элементов множества A, которые не принадлежат множеству B .
Если A ⊂ B , то часто множество A B называют дополнением множества B до A. По определению A A = 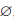
Пример 1.1. Пусть A = {1,3,4,8, 15} ,B = {1,2,7,8, 12}. Тогда
A∪B = {1,2,3,4,7,8,12,15}, A∩B = {1, 8},
AB = {3, 4, 15}, BA= {2, 7, 12}
Определение 1.6. Набор, состоящий из двух элементов x1 и x2, называют упорядоченным, если известно, какой из этих элементов является первым, а какой — вторым. Такой упорядоченный набор называют упорядоченной парой и обозначают (x1, x2). Элементы x1 , x2 называют, соответственно, первой и второй координатами пары (x1, x2). Пары (x1, x2) и (y1 , y2) называют совпадающими, если x1 = y1 и x2 = y2 .
Определение 1.7. Декартовым (или, по-другому, прямым) произведением множеств A и B называют множество упорядоченных пар (x, y), где первый элемент x является элементом множества A, а второй y — элементом множества B . Это множество обозначают символом A × B .
Таким образом, A × B = { (x, y) | x ∈ A, y ∈ B}. Но, вообще говоря, A × B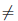
Пусть A и B — числовые отрезки, помещенные на взаимно перпендикулярных осях плоскости. Упорядоченная пара (x, y) — это точка пересечения перпендикуляров, восстановленных в точках x ∈ A и y ∈ B . Произведением A × B является прямоугольник.
Логическая символика
В последующем, как и в большинстве математических текстов используется ряд специальных символов, многие из которых вводятся по мере надобности. Применяются распространенные символы математической логики 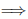
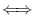
Запись A 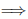
Запись A 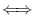
Запись «∃ x ∈ X » означает: существует элемент x из множества X .
Запись «∀ x ∈ X » означает: для любого элемента x из множества X или каков бы ни был элемент x из множества X .
Часто в символьной записи математических утверждений используют символ «:» или эквивалентный ему символ «| которые читают: «такой, что». В частности, запись «∃ x ∈ X : x2 — 1 = 0″ означает: существует такой элемент x в множестве X , что x2 — 1 = 0.
- Заказать решение задач по высшей математике
Множества
Множества и операции над ними
Понятие множества и его элементов
Элемент 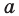
Элемент 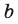

В множестве нет элементов 
Множество можно представить как совокупность некоторых объектов, объединенных по определенному признаку. В математике множество — одно из основных неопределяемых понятий.
Каждый объект, принадлежащий множеству 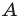
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается
Подмножество
Если каждый элемент множества 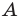
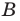
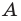
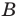
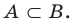
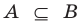
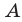
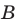
Равенство множеств
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества
Пересечение множеств
Пересечением множеств 
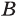

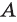
Объединение множеств
Объединением множеств 
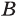


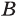
Разность множеств
Разностью множеств 
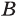


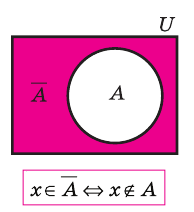
Дополнение множеств
Если все рассматриваемые множества являются подмножествами некоторого универсального множества 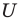




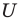
Объяснение и обоснование:
Понятие множества
Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты — элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы — ученики), множестве дней недели (элементы — дни недели), множестве натуральных делителей числа 6 (элементы — числа 1, 2, 3, 6) и т. д. В курсах алгебры и алгебры и начал анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество 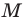
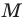
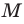
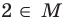
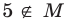
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например, множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом 
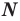

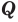
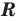
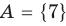
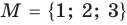
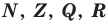
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило — характеристическое свойство, которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, множество 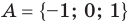
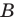

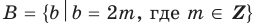
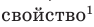
В общем виде запись множества с помощью характеристического свойства можно обозначить так: 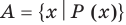
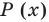
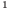
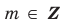
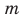
Равенство множеств
Пусть 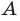
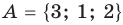
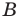
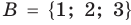
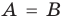
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, 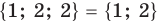
Подмножество
Если каждый элемент множества 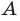
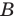
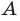
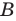
Это записывают следующим образом:
Например, 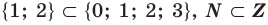
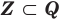
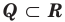
Полагают, что всегда 
Иногда вместо записи 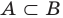
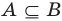
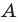
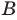
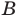
Сопоставим определение равенства множеств с определением подмножества. Если множества 





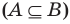




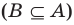
Таким образом, два множества равны, если каждое из них является подмножеством другого.
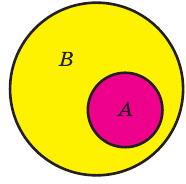
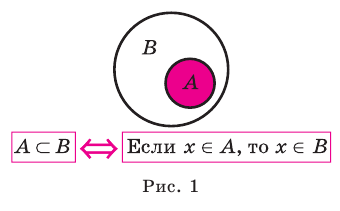
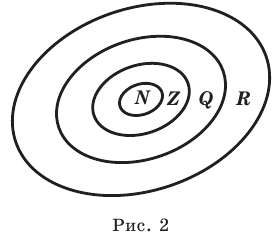
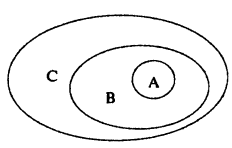
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера—Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами 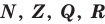
Операции над множествами
Над множествами можно выполнять определенные действия: пересечение, объединение, находить разность. Дадим определение этих операций и проиллюстрируем их с помощью кругов Эйлера—Венна.
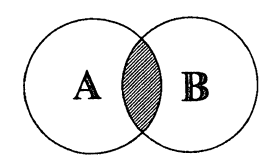
Пересечением множеств 




Пересечение множеств обозначают знаком 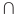
Например, если 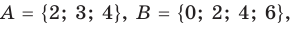
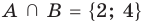
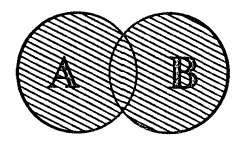
Объединением множеств 




Объединение множеств обозначают знаком 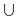
Например, для множеств 

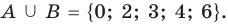
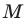
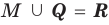
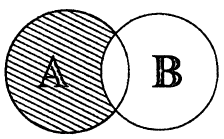
Разностью множеств 



Разность множеств обозначают знаком 
Например, если
Если 



Например, если обозначить множество всех иррациональных чисел через 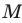
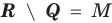
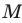
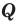
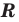
Если все множества, которые мы рассматриваем, являются подмножествами некоторого так называемого универсального множества 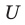
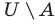
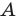
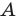
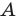
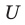
Дополнение множества 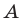
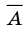
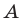
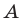
Например, если 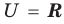
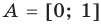
Числовые множества. Множество действительных чисел
Числовые множества:
Действительные числа
Числа, которые можно представить в виде бесконечной десятичной дроби
Рациональные числа
Можно представить в виде несократимой дроби 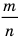
Иррациональные числа
Нельзя представить в виде несократимой дроби 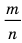
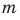
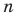
Целые числа
Включают натуральные числа, числа, противоположные им, и число нуль
Дробные числа
Числа, состоящие из целого числа частей единицы
(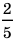
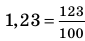
Натуральные числа 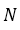
Для школьного курса математики натуральное число — основное не определяемое понятие
Число 0
Такое число, при сложение с которым любое число не изменяется
Целые отрицательные числа
Числа, противоположные натуральным
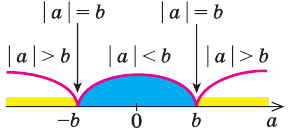
Модуль действительного числа и его свойства
Определение:
Модулем положительного числа называется само это число, модулем отрицательного числа называется число, противоположное ему, модуль нуля равен нулю
Геометрический смысл модуля
На координатной прямой модуль — это расстояние от начала координат до точки, изображающей это число.
Модуль разности двух чисел 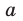
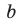
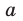
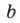
Свойства
1. 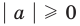
2. 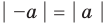
3. 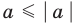
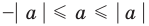
4. При 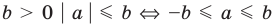
5. При
6. 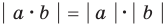
7. 
8. 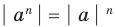
9.
Модуль суммы не превышает суммы модулей слагаемых
10.
Объяснение и обоснование:
Числовые множества
В курсе математики вы встречались с разными числами: натуральными, целыми, рациональными, иррациональными, действительными. Представление о числах у человечества складывалось постепенно, под воздействием требований практики. Например, натуральные числа появились в связи с необходимостью подсчета предметов. Но для того чтобы дать ответ на вопрос «Сколько спичек в пустой коробке из-под спичек?», множества натуральных чисел 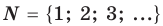
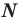
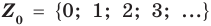
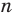
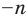
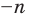
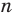
Натуральные числа, числа, противоположные натуральным, и число нуль составляют множество 
Измерение величин привело к необходимости расширения множества целых чисел и введения рациональных чисел. Например, средняя многолетняя температура воздуха в январе в г. Харькове — 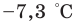
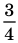
Таким образом, выбирая какую-либо единицу измерения, мы получаем числовое значение величин, которое может выражаться с помощью разных рациональных чисел — целых и дробных, положительных и отрицательных.
Целые и дробные числа составляют множество 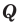
Любое рациональное число можно записать в виде дроби 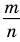
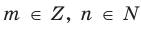
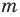
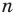
Рациональное число может быть записано разными дробями. Например,
Как видно из приведенных примеров, среди дробей, которые изображают данное рациональное число, всегда есть единственная несократимая дробь (для целых чисел — это дробь, знаменатель которой равен 1).
Обратим внимание, что рациональное число, записанное в виде дроби 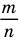
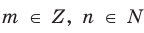
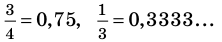
Договоримся, что конечную десятичную дробь можно изображать в виде бесконечной, у которой после последнего десятичного знака, отличного от нуля, на месте следующих десятичных знаков записываются нули, например, 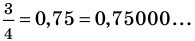
Целые числа также договоримся записывать в виде бесконечной десятичной дроби, у которой справа от запятой на месте десятичных знаков стоят нули, например 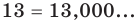
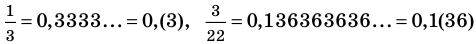
Таким образом, каждое рациональное число может быть записано в виде бесконечной периодической десятичной дроби и наоборот, каждая бесконечная периодическая дробь задает рациональное число.
Обратим внимание, что любая периодическая десятичная дробь с периодом девять равна бесконечной десятичной дроби с периодом нуль, у которой десятичный разряд, предшествующий периоду, увеличен на единицу по сравнению с разрядом первой дроби. Например, бесконечные периодические дроби 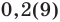
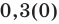
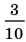
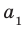
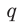
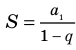
В дальнейшем, записывая рациональные числа с помощью бесконечных периодических десятичных дробей, договоримся исключить из рассмотрения бесконечные периодические дроби, период которых равен девяти.
Каждое рациональное число можно изобразить точкой на координатной прямой (то есть прямой, на которой выбраны начало отсчета, положительное направление и единица измерения). Например, на рисунке изображены несколько рациональных чисел 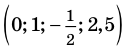
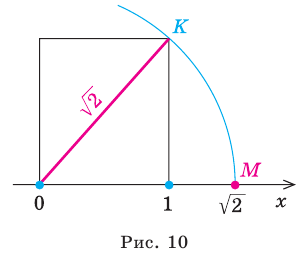
Однако на координатной прямой есть точки, изображающие числа, которые не являются рациональными. Например, из курса алгебры известно, что число 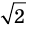
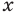
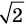
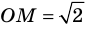
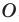
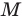
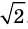
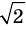
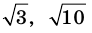
Рациональные и иррациональные числа составляют множество действительных чисел 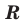
Каждое действительное число может быть записано в виде бесконечной десятичной дроби: рациональные числа — в виде бесконечной периодической десятичной дроби, а иррациональные — в виде бесконечной непериодической десятичной дроби.
Напомним, что для сравнения действительных чисел и выполнения действий над ними (в случае, когда хотя бы одно из них не является рациональным) используются приближенные значения этих чисел. В частности, для сравнения двух действительных чисел последовательно рассматриваем их приближенные значения с недостатком с точностью до целых, десятых, сотых и т. д. до тех пор, пока не получим, что какое-то приближенное значение одного числа больше соответствующего приближенного значения второго. Тогда то число, у которого приближенное значение больше, и считается большим. Например, если
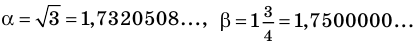
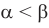
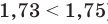
Для выполнения сложения или умножения рассмотренных чисел 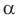
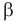
Как видим,
В курсе математического анализа доказывается, что в случае, когда приближенные значения чисел 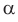
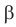
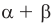
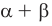
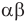
Модуль действительного числа и его свойства
Напомним определение модуля.
Модулем положительного числа называется само это число, модулем отрицательного числа — число, противоположное ему, модуль нуля равен нулю.
Это определение можно коротко записать несколькими способами. а при а > 0,
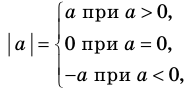
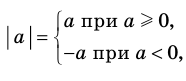
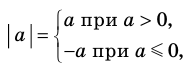
При необходимости мы будем пользоваться любой из этих записей определения модуля. Для нахождения 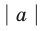
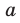
На координатной прямой модуль числа — это расстояние от начала координат до точки, изображающей это число.
Действительно, если 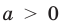
Если 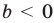
Модуль разности двух чисел 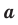
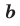
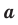
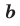
Для доказательства можно воспользоваться тем, что при параллельном переносе вдоль оси координат на 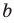
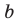
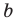
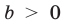
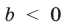
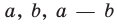
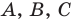

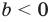
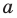
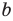
При параллельном переносе вдоль оси 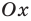
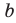
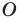
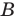
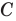
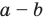
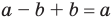
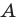
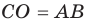
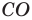
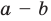
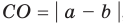
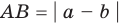
Используя определение модуля и его геометрический смысл, можно обосновать свойства модуля, приведенные в таблице 2.
Например, учитывая, что 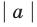
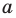
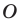
то есть модуль любого числа является неотрицательным числом.
Учитывая, что точки 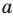
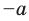
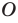
это означает, что модули противоположных чисел равны.
Если 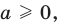
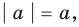
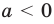
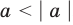
то есть каждое число не превышает его модуль.
Если в последнее неравенство вместо 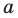
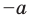
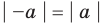
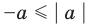
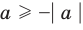
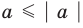

При 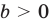

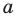
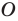
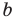
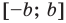
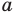
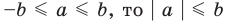
при 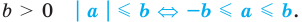
Обратим внимание, что последнее утверждение справедливо и при 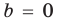
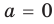
Аналогично при 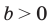
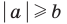
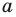
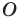
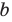
то есть в этом случае 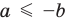
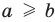
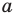
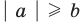

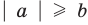

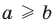
при
Свойства модуля произведения и модуля дроби фиксируют известные правила действий над числами с одинаковыми и разными знаками:
модуль произведения равен произведению модулей множителей, то есть
модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю), то есть
Формулу для нахождения модуля произведения можно обобщить для случая нескольких множителей
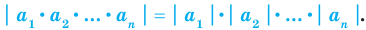
Если в формуле (3) взять 
Используя последнюю формулу справа налево при 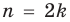
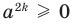
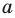
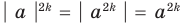
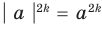
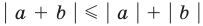
запишем неравенство (1) для чисел 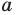
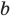
Складывая почленно эти неравенства, получаем
Учитывая неравенство (2), имеем

то есть модуль суммы не превышает суммы модулей слагаемых. Если в неравенстве (4) заменить 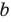
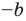
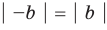
Если записать число 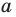
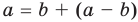
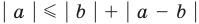

Если в неравенстве (6) заменить 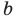
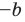
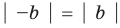

то есть модуль суммы двух чисел не меньше разности их модулей.
Меняя местами буквы 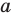
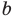
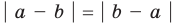

Полученные неравенства (4)-(8) можно коротко записать так:
Примеры решения задач:
Пример №402
Докажите, что сумма, разность, произведение, натуральная степень и частное (если делитель не равен нулю) двух рациональных чисел всегда является рациональным числом.
Решение:
► Пусть заданы два рациональных числа 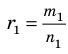
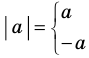
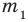
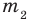
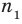
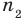
где 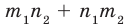
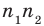
Комментарий:
Любое рациональное число может быть записано как дробь 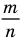
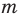
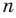
Чтобы доказать утверждение задачи, достаточно доказать, что сумма, разность, произведение и частное двух дробей вида 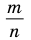
Пример №403
Докажите, что для любого натурального числа 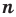
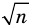
Комментарий:
Для доказательства утверждения задачи можно использовать метод от противного: предположить, что заданное положительное число является рациональным ненатуральным (то есть дробью), и получить противоречие с условием или с каким-либо известным фактом.
Записывая 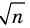
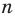
Решение:
► Допустим, что 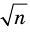
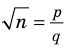
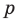
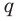
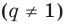
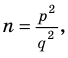
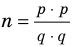
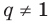
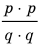
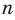
Следовательно, у натуральных множителей, которые стоят в числителе и знаменателе этой дроби, должен быть общий натуральный делитель, отличный от 1. Но в числителе стоят только множители 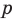
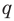

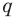
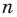
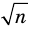
Например, поскольку числа 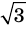
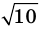
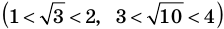
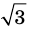
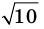
Пример №404
Докажите, что 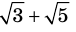
Решение:
► Допустим, что число 
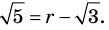
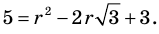
Следовательно,
Но правая часть этого равенства — рациональное число (поскольку по предположению 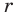
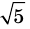
Комментарий:
Для доказательства утверждения задачи можно использовать метод «от противного» — допустить, что заданное число является рациональным, и получить противоречие с каким-либо известным фактом, например с тем, что 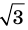
При анализе полученных выражений используем результат задачи 1: если число 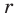
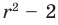
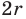
Заметим, что знаменатель полученной дроби
Пример №405
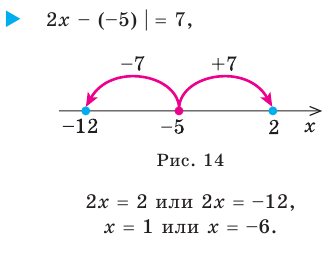
Решите уравнение
Решение
I способ
►
Ответ:
Комментарий:
Заданное уравнение имеет вид 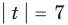
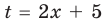
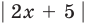
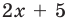
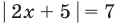
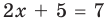
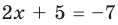
II способ
Ответ:
Комментарий:
С геометрической точки зрения 
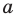
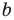
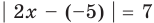
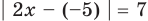
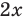
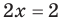
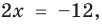
Пример №406
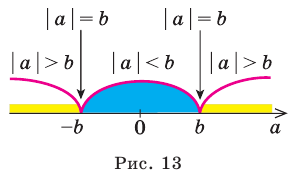
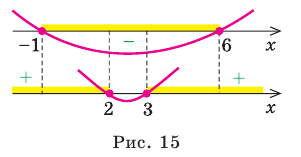
Решите неравенство
Решение:
Решая эти неравенства (рис. 15), получаем
Следовательно, 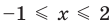
Ответ:
Комментарий:
Заданное неравенство имеет вид 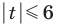
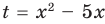
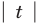
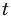
Тогда неравенству 
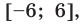
- Рациональные уравнения
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Функции, их свойства и графики
- Параллельность в пространстве
- Перпендикулярность в пространстве
- Векторы и координаты в пространстве
Математика — это точная абстрактная наука, оперирующая своими специальными понятиями, структурами и символами. Основными методами в математических исследованиях являются строгие логические рассуждения, а объектами изучения — математические модели. Но абстрактность математики не означает ее отрыв от реальной жизни. Реальные задачи описываются в математических терминах, как правило в безразмерном виде. Это есть так называемая
математическая модель явления. При решении уже поставленной математической задачи используются абстрактные математические методы.
Одна и та же математическая модель может описывать свойства различных реальных явлений. Само реальное явление рассматривается вновь после решения математической задачи и ее анализа, на основании которого могут быть сделаны выводы
не только о состоянии явления, но и о его развитии. В этом смысле без математики нет науки. Еще великий Леонардо да Винчи писал: «Никакой достоверности нет в науках там, где нельзя применить ни одну из математических наук, ив том, что не имеет связи с математикой.» И еще: » Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства.»
Математические методы играют огромную роль в образовании современного высококвалифицированного специалиста в технических областях, предоставляя ему аппарат исследования, дисциплинируя, приучая к строгим логическим рассуждениям.
Поскольку язык и методы математики широко используются при современном преподавании всех естественно-научных и технических дисциплин, математика изучается с первого семестра в любом высшем техническом учебном заведении, и на нее выделяется значительная часть бюджета времени студента.
Под множеством понимают любой набор определенных и различимых между собой объектов, рассматриваемых как единое целое. Это высказывание не является определением, поскольку слово « множество» заменено словом «набор». Близкими к понятию «множество» являются понятия: собрание, совокупность, комплекс, система и т. п. Вместе с тем здесь имеется три важных момента.
Объекты, входящие во множество, определенные (т. е. для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет), различимы между собой (во множестве не может быть двух или более одинаковых объектов) и все объекты, входящие во множество, мыслятся как единое целое (все объекты рассматриваются в совокупности, а от свойств отдельных объектов абстрагируются).
Множества обозначают прописными буквами латинского алфавита. Объекты, входящие во множество, называют элементами и их обозначают строчными буквами. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае множество называется бесконечным.
Множество может быть задано при помощи правила, позволяющего определить, является ли данный объект элементом множества или нет. В записи правило, задающее множество, отделено вертикальной чертой. Например, пусть множество В есть множество решений уравнения 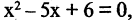
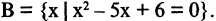
Конечное множество может быть задано перечислением входящих в него и разделенных запятой элементов, например, 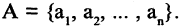
мента, называется пустым и обозначается символом 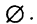
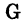
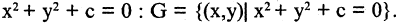
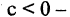
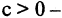
Для указания того факта, что объект принадлежит данному множеству, используют знак 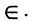
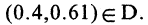
Множество В называется подмножеством множества А, если каждый элемент В одновременно является элементом множества А. Это записывается так:
Пример:
Пусть заданы множества 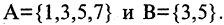
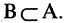
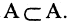
Пример:
Если 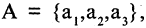
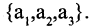
Если конечное множество А состоит из п элементов, то оно имеет ровно 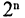
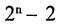
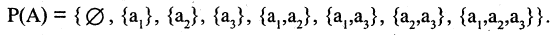
Замечание. Не следует путать символы 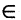

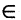

Зафиксированное каким-либо образом множество объектов, допустимых при данном рассмотрении, называют базовым или универсумом. Базовое множество обозначают буквой 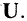
Операции над множествами
Множества можно складывать и вычитать, то есть совершать операции.
Равенство множеств
Множества А и В считаются равными, если они состоят из одних и тех же элементов. Равенство множеств обозначают так: А=В. Если множества не равны, то пишут: А 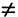
Пример. Доказать, что множество 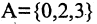
Для доказательства решим уравнение. Получим: 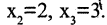
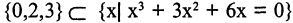
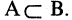
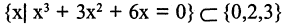
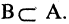
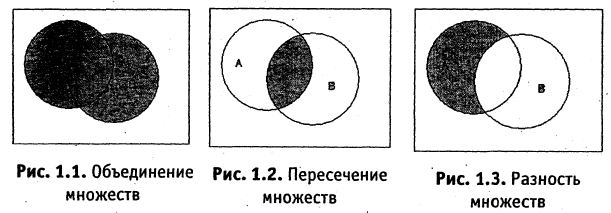
Объединение (сумма) множеств
Объединением множеств А и В называется такое множество С, каждый элемент которого содержится хотя бы в одном из множеств А или В. Обозначается: 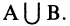
Можно рассматривать объединение 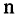
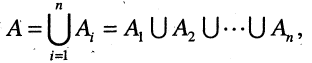
при этом в А входят все элементы, которые входят хотя бы в одно из множеств 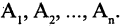
ствительных чисел 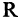
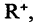
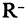
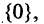
Для наглядного представления соотношений между несколькими подмножествами какого-либо универсума часто используются круги Эйлера или диаграммы Венна. Универсум представляется множеством всех точек некоторого прямоугольника, а его подмножества — соответствующими кругами. Операция объединения и другие операции иллюстрируются кругами Эйлера представленными на рис. 1.1-1.5.
Пересечение (умножение) множеств
Пересечением множеств А и В называется множество D, составленное из общих для множеств А и В элементов. Обозначение: 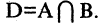
Можно рассматривать пересечение 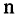
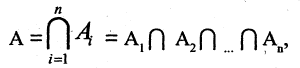
при этом в А входят только те элементы, которые входят во все множества 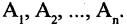
Пусть есть некоторое множество А. Говорят, что задано разбиение множества А на классы 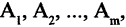
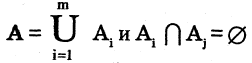
для всех 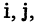

Классы — это такие подмножества разбиваемого множества, которые не имеют общих элементов, а их объединение образует исходное множество А. Следовательно, каждый элемент множества А входит в один и только в один класс.
Разность двух множеств
Разностью двух множеств А и В называется множество G, содержащее лишь те элементы из А, которые не входят в В. Обозначение: 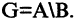
Если В — подмножество 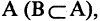
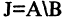
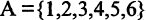
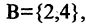
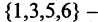
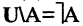
Пример. Пусть 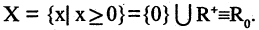
Тогда 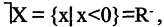
Операции над множествами подчиняются определенным законам. Перечислим их.
1.Коммутативный или переместительный закон

2.Ассоциативный или сочетательный закон
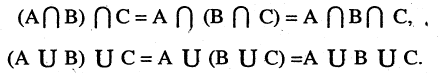
Так как порядок выполнения операций несущественен, то скобки в записи опускают.
3.Дистрибутивный или распределительный закон:
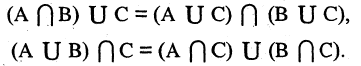
4.Закон идемпотентности:
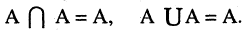
5.Закон поглощения:
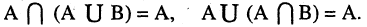
6.Закон двойственности де Моргана:

10.Если 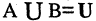
Из законов (1-12) следует принцип двойственности: всякое равенство, тождественно выполняемое в теории множеств, переходит также в тождественно выполняющееся равенство при замене знака объединения 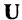
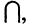
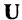
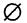
Прямое произведение множеств
Кортежем называют любую выделенную упорядоченную совокупность объектов (элементов кортежа). Синонимами понятия «кортеж» являются: упорядоченная система, упорядоченная совокупность, вектор, упорядоченный набор, «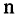
одинаковую длину, и все их соответствующие компоненты совпадают.
Элементы, составляющие кортеж, называются компонентами, которые в силу упорядоченности имеют номер: первый компонент, второй компонент, … 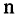
Примеры кортежей: 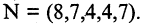
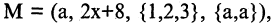
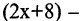
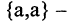
Прямым произведением двух множеств А и В (обозначается 
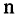
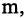
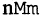
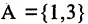
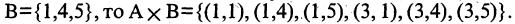
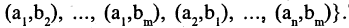
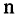
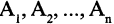
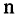
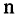
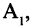
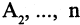
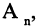
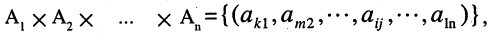
где 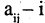
Если все множества 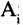
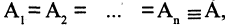
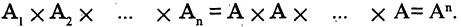
Например: пусть R — множество действительных чисел, тогда 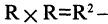
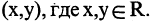
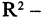
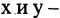
каждый его элемент является упорядоченной парой, следовательно, любое подмножество множества 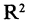
Проекцией кортежа 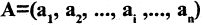
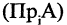
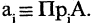
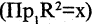
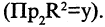
Пример:
Пусть А — отрезок [1,3], В — отрезок [2,5]. Тогда 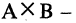
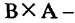
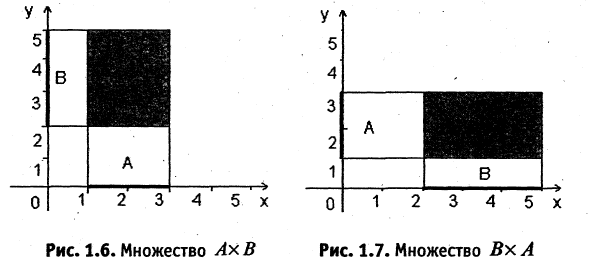
Пример:
Пусть А — множество, элементами которого являются буквы, цифры и все знаки операций и препинания. Такое множество называют алфавитом. Тогда 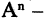
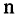
Природа компонентов прямого произведения обычно отличается от природы элементов сомножителей. Например, пусть Q — множество участников шахматного турнира, тогда 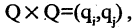
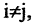
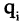
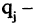
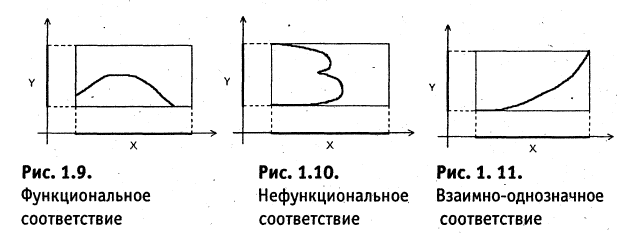
Понятие соответствия
Пусть заданы два множества 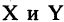
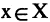
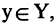
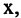
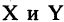
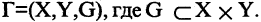
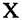
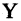
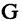
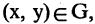
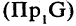
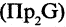
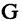
Два соответствия равны тогда и только тогда, когда равны их области отправления, области прибытия и графики. Пример. Заданы четыре разных соответствия, имеющие одинаковые области отправления и прибытия:
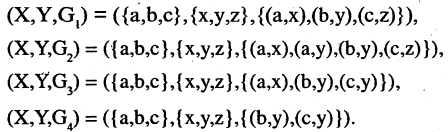
На рис. 1.8а, 1.86, 1.8в, и 1.8г. различия этих соответствий видны достаточно наглядно.
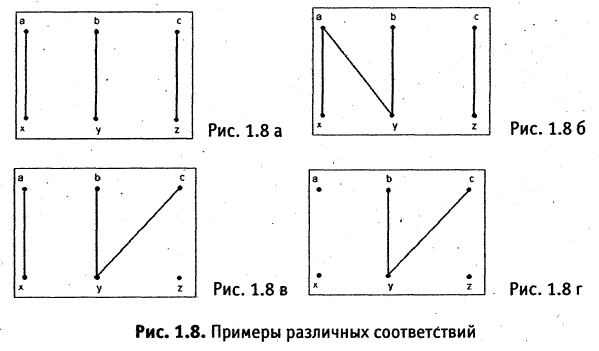
В соответствии 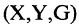
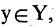
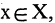
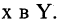
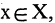
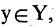
Соответствие называется всюду определенным, если множество 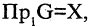
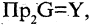
Соответствие 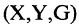
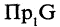
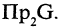
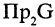
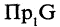
Соответствие между 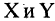
Пусть 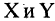
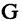
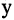
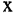
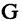
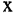
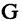
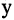
Мощность множества
Мощность множества характеризует количество элементов этого множества. Множества равномощны, если между их элементами можно установить взаимно-однозначное соответствие. Число элементов в конечном множестве А называется кардинальным числом и обозначается |А|. Подсчет элементов конечного множества заключается в установлении взаимно-однозначного соответствия между этими элементами и конечной последовательностью натуральных чисел.
Множество называется бесконечным, если оно равномощно хотя бы одному из его собственных подмножеств. Бесконечное множество А называется счетным, если оно равномощно множеству всех натуральных чисел N. Примеры счетных множеств: множество целых чисел, четных чисел, рациональных чисел. Счетное множество образуется при объединении счетного множества конечных множеств (например, множество слов в любом конечном алфавите) и т. д. Счетным будет и объединение счетного множества счетных множеств (множество всех векторов с натуральными компонентами). Множество А называется не более чем счетным, дискретным, если оно конечно (в частности, пусто) или счетно. Счетное множество среди бесконечных множеств имеет наименьшую мощность.
Рассмотрим все вещественные числа на отрезке 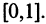
единичного отрезка числовой оси, имеет мощность континуума (непрерывное множество). Мощность множества континуума превышает мощность счетного множества. Любой конечный отрезок числовой оси равномощен единичному отрезку. Более того, любой конечный отрезок равномощен и всей числовой оси. Например, между отрезком 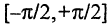
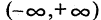
Множества наибольшей мощности не существует. Это следует из того, что мощность любого множества А всегда строго меньше мощности множества всех его подмножеств
Множества — основные понятия
Под множеством понимается совокупность каких-либо объектов, называемых элементами этого множества. Например, можно говорить о множестве студентов данного вуза, множестве учебников по математике, множестве треугольников, множестве действительных чисел и т. д. Множества, содержащие конечное число элементов, называются конечными (множество студентов, множество учебников). Множества с бесконечным числом элементов называются бесконечными (множество треугольников, множество действительных чисел).
Множество обычно обозначается заглавными латинскими буквами A, B, С, …, а их элементы — малыми а, b, с, ….
Утверждение ’’элемент х принадлежит множеству А” записывается так : «х ∈ А ”, а противоположное утверждение ” элемент х не принадлежит множеству А” записывается так : ”х ∉ А ”.
Определение:
Если все элементы множества А принадлежат также множеству В, то говорят, что ” А содержится в В” или: ” А является подмножеством В”, и записывают так: A ⊂ В.
Определение:
Два множества называются равными (совпадающими), если они состоят из одних и тех же элементов: A = B.
Пример:
Сформулируйте словами утверждение:
A=B⇔ A ⊂ B и B ⊂ A и докажите его.
Конечное множество можно задать перечислением его элементов. Так, запись A = {1;2;3} означает, что множество А состоит из трех чисел 1,2,3. При этом порядок перечисления элементов не играет роли: {1;2;3} = {3;2;1}.
Бесконечное множество можно задать, написав условие, которое выполняется для всех элементов данного множества и не выполняется для других. Запись
В = {x | 1 < х < 2}
означает множество всех чисел, больших одного, но меньших двух, т.е. интервал (1;2).
Множество удобно схематически изображать в виде ’’диаграмм Эйлера” — геометрических фигур на плоскости, взаимное расположение которых отражает отношение между множествами. Так, например, если A ⊂ B и B ⊂ C, то A изображается частью В₁ а В частью C (рис. 1). C помощью диаграммы Эйлера на рис. 1 наглядно видно свойство транзитивности операции включения множеств: A ⊂ B ⊂ C ⟹ A ⊂ C.
Определение:
Множество называется пустым, если оно не содержит ни одного элемента. Пустое множество обозначается символом ⊘.
Так, например, множество отрицательных натуральных чисел пусто.
Операции над множествами
Определение:
Пересечением множеств A и B называется множество С, состоящее из всех элементов, одновременно входящих и в А, и в В. Это записывается следующим образом: A ∩ В = С.
Иллюстрация пересечения двух множеств с помощью диаграмм Эйлера приведена на рис. 2, где множество C заштриховано.
Пример:
Если множество А есть интервал (1 ;5) а множество В есть интервал (2;7), то пересечение множеств A и B есть интервал (2;5).
Свойства операции пересечения множеств приведем без доказательств:
- A ∩ В = В ∩ А(коммутативность).
- A ∩ (В ∩ С) = (A ∩ В) ∩ C = A ∩ В ∩ С(ассоциативность).
- A ⊂ В ⟹ А ∩ В = А.
- A∩A= А.
- A ∩ ⊘ = ⊘
Определение:
Объединением множеств A и B называется множество С, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств или А, или В, или A u B одновременно. Это обозначается следующим образом : A ∪ В = С.
Иллюстрация объединения с использованием диаграмм Эйлера приведена на рис. 3, где множество C заштриховано.
Пример:
Если множество А есть отрезок [1;3], множество В есть отрезок [2;5], то A ∪ B есть отрезок B=[1;5].
Свойства операции объединения множеств приведем без доказательств:
1) A ∪ B=B ∪ A (коммутативность).
2) A ∪ (B∪C)=(A ∪ B) ∪ C=A ∪ B ∪ C (ассоциативность).
3) A∩(B∪C)=(A∩B) ∪ (A∩C) (дистрибутивность).
4) A ⊂ B ⇒A ∪ B=B.
5) A ∪ A=A.
6) A ∪ ⊘=A.
Определение:
Разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множеству А, но не принадлежащих В. Разность A u B обозначается АВ и изображена штриховкой на рис. 4.
Операция вычитания множеств не коммутативна : A∖B≠B∖A.
Пример:
Если А = (1; 10), В = (3; 20), то АВ=(1;3], ВА =[10,20).
Кванторы общности и существования
При изложении материала мы будем использовать знак 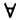
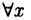
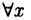
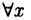
Обозначение Ǝх означает: ’’существует такое х, что …”, ”по крайней мере для одного х…”, запись Ǝх > 0 читается: ’’существует такое положительное число х, что…”, запись Ǝх₁ ,x₂ Є M означает: ’’существуют такие х₁ ,x₂ — элементы множества М, что …”.
Нам также неоднократно придется использовать символы ⇒ и ⇔.
Запись логического следования А ⇒ В означает, что если верно утверждение А, то верно и утверждение В, то-есть из А следует В.
Запись логической равносильности ⇔ означает, что из А следует В и наоборот, из В следует А.
Так, например, запись: 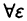
Необходимое и достаточное условие
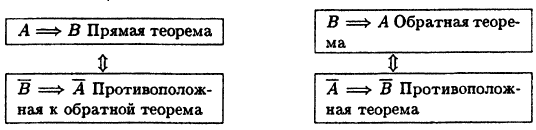
Любая теорема может быть сформулирована в виде: если выполняется условие А, то верно утверждение В. Будем называть это прямой теоремой и схематически запишем в виде:
Теорема:
А ⇒ В.
В качестве примера приведем теорему, называемую достаточным условием экстремума непрерывной функции, изучаемую в курсе математики средней школы.
Теорема:
Если функция f непрерывна в точке а и производная f меняет знак при переходе через эту точку, то а является точкой экстремума функции f.
Условие А стоит после слова «если», утверждение В написано после
слова «то».
Определение:
А называется достаточным условием для
выполнения В. В свою очередь, В является необходимым условием для выполнения А.
Применительно к теореме 1.2 это выглядит следующим образом.
Достаточным условием для существования экстремума непрерывной функции f в точке а является изменение знака ее производной при переходе через эту точку.
Для лучшего усвоения введенных понятий рассмотрим очевидно справедливое утверждение не из области математики.
Теорема:
Если человек здоров, то у него есть голова.
Здесь здоровье является достаточным условием наличия у человека головы. Наоборот, наличие головы является необходимым условием здоровья. Подумайте, будет ли это условие достаточным для того, чтобы человек был здоров? Реально ли вообще сформулировать достаточное условие того, что человек здоров?
Обозначим А утверждение, заключающееся в отрицании утверждения А(читается «не А»). Если справедлива прямая теорема 1.1, то методом «от противного» легко можно доказать справедливость следующего утверждения, которое называется
«противоположная к обратной теорема»:
Теорема:
В ⇒ А.
Доказательство:
Имеем А ⇒ В, нужно доказать, что В⇒ А Предположим противное: В ⇒ А, но в соответствии с теоремой 1.1 А ⇒ В. Полученное противоречие (В ⇒ В) доказывает теорему.
Аналогично можно доказать, что если справедлива теорема 1.4, то верна теорема 1.1, т. е. эти утверждения равносильны.
Для теоремы 1.2 противоположной к обратной будет теорема: ’’Если точка а не является точкой экстремума функции f ̕ непрерывной в этой точке, то производная f ̕ не меняет знак при переходе через эту точку”.
Для теоремы 1.3 противоположным к обратному будет утверждение: ’’Если у человека нет головы, то он не здоров”.
Проведите доказательство этого утверждения самостоятельно методом ”от противного».
Наряду с прямой теоремой 1.1 можно рассмотреть утверждение, называемое «обратной теоремой” :
Теорема:
В ⇒ А.
Однако обратная теорема не всегда справедлива, если верна прямая. Так, например, для теоремы 1.3 обратное утверждение: «Если у человека есть голова, то он здоров”, очевидно, не верно.
Если все же теорема 1.5 справедлива, то методом «от противного” исходя из нее доказывается справедливость утверждения, называемого «противоположная теорема”:
Теорема:
А ⇒ В
Наоборот, из теоремы 1.6 вытекает справедливость теоремы 1.5, т.е. эти утверждения равносильны. Заметим, что из прямой теоремы 1.1 не обязательно следует справедливость противоположной теоремы 1.6.
Приведенные связи удобно запоминать, представляя себе следующий ’’логический квадрат» (рис. 5):
Если наряду с прямой теоремой выполняется также обратная теорема, то А является ’’необходимым и достаточным” условием для В. То же самое можно сказать про В по отношению к А.
Так, например, то, что треугольник прямоугольный, является необходимым и достаточным условием того, что квадрат одной из сторон равен сумме квадратов двух других.
Множество N натуральных чисел
Определение:
Числа 1,2,3,… называются натуральными.
Сумма и произведение натуральных чисел будет числом натуральным, а разность и частное — не всегда. При вычитании натуральных чисел может получится отрицательное число, а при делении — не целое. Например, при делении 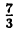
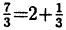
Приводя к общему знаменателю, получим равенство: 7 = 2 ∙ 3 + 1. В этих равенствах 7 называется делимым, 3 — делителем, 2 — целой частью и 1 — остатком (остаток всегда меньше делителя). Если остаток равен нулю, то говорят, что делимое делится на делитель, как, например, 6 делится на 3. Если натуральное число, большее единицы, делится только на 1 и на себя (что всегда справедливо), то оно называется простым. Простыми числами являются числа 2,3,5,7,11,13,17,19,23 и т. д. Любое натуральное число может быть представлено в виде произведения простых сомножителей. Например : 12 = 1 ∙ 2 2 3, 18 = 1 2 ∙ 3 3, 7 = 1 ∙ 7 и т. д.
Определение:
Наименьшим общим кратным двух данных натуральных чисел называется наименьшее из чисел, которые делятся на каждое из них.
Для любых двух натуральных чисел всегда найдется наименьшее общее кратное, поскольку их произведение всегда делится на каждое из двух данных.
Наименьшее общее кратное 12 и 18 равно 36. Для того чтобы найти наименьшее общее кратное двух чисел, нужно первое число помножить на простые множители, входящие в разложение второго числа и не входящие в разложение первого: 12 ∙ 3 = 36.
Определение:
Наибольшим общим делителем двух данных натуральных чисел называется наибольшее из чисел, на которые делится каждое из них.
Для любых двух натуральных чисел всегда найдется наибольший общий делитель, поскольку любые два числа всегда делятся на единицу. Если у двух натуральных чисел нет других общих делителей кроме единицы, они называются взаимно простыми. Наибольший общий делитель 12 и 18 равен 6. Для того, чтобы найти наибольший общий делитель двух чисел, нужно перемножить общие простые множители, входящие в разложение и одного, и другого числа: 1 ∙ 2 ∙ 3 = 6.
Множество Z целых чисел
Определение:
Натуральные, отрицательные натуральные числа и ноль образуют множество целых чисел (множество Z).
Сумма, произведение и разность целых чисел является целым числом, а частное — не всегда. Иногда множество отрицательных целых чисел обозначается Z_.
Множество натуральных чисел является подмножеством множества целых чисел: N ⊂ Z.
Множество Q рациональных чисел
Определение:
Рациональными числами называются числа вида 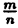
Множество целых чисел является подмножеством множества рациональных чисел, т. к. любое целое число m можно рассматривать как рациональное, представив в виде 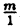
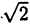
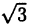
Всякое рациональное число 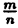
Пример:
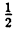
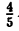
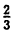
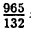
Две последние десятичные дроби бесконечные периодические. Повторяющиеся цифры называются периодом дроби и пишутся в скобках, количество этих цифр называется длиной периода. Для обратного преобразования конечной десятичной дроби ее нужно представить в виде простой и сократить: 0,8=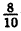
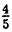
Перевод периодической десятичной дроби в простую объясним на примере.
Пример:
Записать в виде простой дроби 0,(6).
Решение:
Периодическую дробь 0,(6) обозначим за x: 0,(6)=x, тогда, т. к. 10‧х — 10-0,666… = 6,666…, легко заметить, что 10∙х = 6 х. Решая это уравнение, получаем: 9‧x=6⇔x =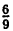
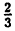
Определение:
Целой частью числа называется наибольшее целое число, не превосходящее данное. Целая часть числа х обозначается [x].
Примеры:
[3,56]=3; [0,12]=0; [-0,12]=-1; [-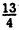
[5]=5; [0]=0.
Определение:
Дробной частью числа называется разность между самим числом и его целой частью. Дробная часть числа обозначается {x}. Она строго меньше единицы и находится в пределах : 0 ≤ {x} < 1.
Примеры:
{3,56}=0,56; {0,12}=0,12; {-0,12}=0,88;
{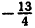
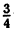
Множество J иррациональных чисел
Определение:
Иррациональным числом называется бесконечная непериодическая десятичная дробь.
Примерами иррациональных чисел являются √2, √3, ∛11, π, е, и т. д. Заметим, что J ∩Q = ⊘ Иррациональное число нельзя представить в виде простой дроби, его также невозможно ’’выписать до конца” (представить в виде конечной десятичной дроби), поэтому запись √2 = 1,41 ошибочна, следует писать √2 ≈ 1,41.
Заданное бесконечной непериодической дробью иррациональное число определяет две последовательности конечных (рациональных) десятичных дробей, называемых десятичными приближениями по недостатку и по избытку. Например, для √2 можно написать:
1 √2<2,
1,4< √2<1,5,
1,41< √2<1,42.
…
В инженерных расчетах при замене иррациональных чисел их рациональными приближениями достаточно во всех вычислениях брать на один знак больше, чем требуется в результате, и затем округлить результат.
Для иррациональных чисел можно также определить целую и дробную части, причем для х ∈ J ⇒ {τ} ∈ J.
Множество R действительных чисел
Определение:
Все рациональные и иррациональные числа образуют множество действительных (вещественных) чисел: R = QuJ.
В множестве действительных чисел всегда выполнимы сложение, вычитание, умножение, деление (не на ноль), возведение в любую действительную степень положительного числа, извлечение корня нечетной степени из отрицательного числа.
В множестве действительных чисел невозможно извлечение корня четной степени из отрицательного числа.
Числовая ось
Множеству действительных чисел можно дать простую геометрическую интерпретацию. Выберем на прямой положительное направление (указывается стрелкой), начало отсчета и единицу масштаба. Такая прямая называется числовой осью. Каждой ее точке можно поставить в соответствие единственное действительное число следующим образом: положительное число х изображается точкой, расположенной на оси на расстоянии х в направлении стрелки (на рис. 6 справа от О), отрицательное с другой стороны (на рис. 6 слева от О) на расстоянии х от О.
Число х называется координатой соответствующей точки на числовой оси. Из двух чисел больше будет то, которое расположено на числовой оси дальше в направлении стрелки (на рис. 6 — правее).
Например, -1 > -2.
Числовые промежутки
Если известны два действительных числа а и b, a < b, то можно определить следующие множества действительных чисел, находящихся между двумя данными — числовые промежутки.
Отрезок (сегмент) [α; b]= {x | a ≤ х ≤ b},
Интервал (a; b)= {x | a < х < b}.
В частности, можно рассматривать бесконечные интервалы:
(- ∞; +∞)={x∈R}, (a;+∞)={x|x>a}, (- ∞ ;b)={x|x<b}.
Полуинтервал, [a;b)={x∣a≤x<b}, (a;b]={x∣a<x≤b}.
В частности, можно рассматривать бесконечные полуинтервалы: [a;+∞)={x∣x≥a}, (-∞;b]={x∣x≤b}.
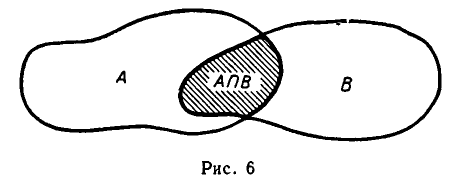
Числовые промежутки изображают на числовой оси, причем если граничная точка принадлежит промежутку — она закрашена, если нет — изображается светлым кружком (’’выкалывается”). На рис 7 изображен полуинтервал (2;5].
Числовые промежутки будем выделять штриховкой или утолщенной линией.
Примеры с решением на тему: «Множества«
При решении примеров данного практического занятия используется материал средней школы и материал лекции 1. Применение метода интервалов для решения неравенств иллюстрируется примерами 1.2-1.5
Пример:
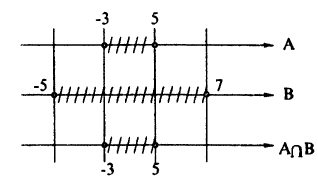
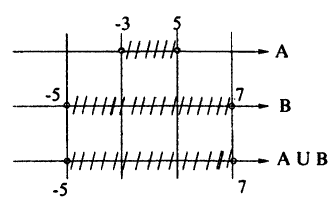
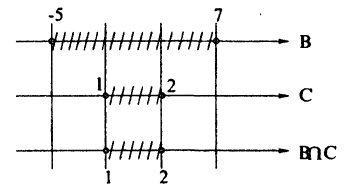
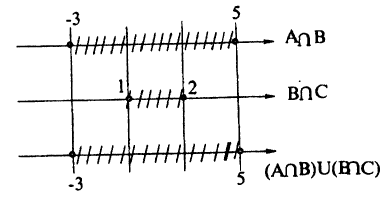
Пусть A = [-3;5],B = (-5;7),C = [1;2). Найдите множество: A₀ = (4 ∩ В) U (В ∩ С).
Решение:
Для нахождения результата операций над числовыми промежутками их удобно изображать на числовых осях, расположенных одна под другой с согласованным началом и одинаковым масштабом. Если исходные промежутки А и В заштриховать, то их пересечением будет множество точек, заштрихованных на каждой из осей (рис. 8), а их объединением — множество точек, заштрихованных хотя бы на одной из осей (рис. 9).
Пользуясь этим правилом, последовательно получим A ∩ В, В ∩C и, наконец, (Л ∩ В) ∪ (В ∩ С) (рис. 8, 10, 11).
Ответ: A₀ ≈ [-3; 5].
Пример:
Найдите элементы множества:
A₀ = {x | (2 — 3x)(x + 4)(x — 2) > 0}.
Решение:
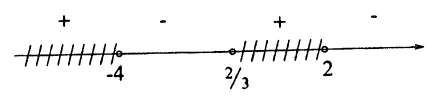
Неравенство (2 — 3x)(х + 4)(x — 2) > 0 решим методом интервалов, для чего нанесем на числовую ось значения х, при которых левая часть неравенства обращается в ноль: x₁ =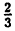
Сами эти значения не удовлетворяют неравенству, поэтому соответствующие точки “выколоты».
Знаки выражения в левой части неравенства определим, подставляя в него по одному значению из каждого интервала, на которые все множество R разбилось точками x₁,x₂,х₃. Отметим штриховкой те интервалы, на которых выражение в левой части неравенства положительно. Это множество является искомым.
Ответ: A₀=(-∞; -4) ∪ (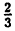
Пример:
Задайте характеристическим свойством множество: A₀ — множество всех натуральных чисел, меньших 5 или больших 10.
Решение:
В условии требуется,чтобы натуральные числа были меньше 5 или больше 10, т.е. искомое множество есть объединение двух подмножеств: множества натуральных чисел, меньших 5 и больших 10.
Ответ: A₀ = {x|x < 5, х ∈ N} ∪ {x|x > 10, х ∈ N}.
Пример:
Решите систему неравенств:
Решение:
Решение системы неравенств есть пересечение множеств решений каждого из входящих в систему неравенств. Аналогично тому, как это делалось при решении примера 1.2, решим каждое из неравенств системы методом интервалов и найдем их пересечение (рис 13).
Ответ: х ∈ (-1; 2,5).
Пример:
Решите совокупность систем неравенств:
Решение:
Решение совокупности систем неравенств есть объединение решений каждой системы, входящей в совокупность. Для решения разложим каждый многочлен в произведение с помощью корней:
Решение совокупности систем методом интервалов представлено на рис. 14
Ответ: х ∈ (-2; 1)
Множества
Понятие множества является одним из основных понятий математики. Оно не сводится к другим понятиям и не определяется. Вместо определения приводят лишь примеры, поясняющие его смысл. Так, можно говорить о множестве всех учеников данной школы, о множестве всех собак на земном шаре, о множестве всех клеток данного человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех натуральных чисел, о множестве всех треугольников на данной плоскости, о множестве всех точек данного круга и т. д.
Когда в математике говорят о множестве, то объединяют некоторые предметы в одно целое — множество, состоящее из этих предметов. Основатель теории множеств Георг Кантор (1845—1918) выразил это следующими словами: «Множество есть многое, мыслимое как единое».
Предметы (объекты), составляющие некоторое множество, называются его элементами. То обстоятельство, что объект а является элементом множества А, записывается так: 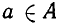
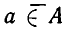
Например, если А есть множество всех четных натуральных чисел, то
Множество иногда можно задать перечислением всех его элементов. В этом случае употребляют фигурные скобки, в которые помещают названия всех элементов множества, разделенные запятыми. Так, {1, 2, 3) обозначает множество, состоящее из чисел «один», «два», «три» и только из них.
Вообще некоторое множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называется характеристическим свойством множества.
Характеристическим свойством множества {1, 2, 3) может быть свойство совпадать с одним из членов списка, приведенного в фигурных скобках. Другим характеристическим свойством этого же множества является свойство быть корнем уравнения
Числовые множества
Множества могут состоять из объектов самой различной природы. Их элементами могут быть буквы, атомы, числа, уравнения, точки, углы и т. д. Именно этим объясняется чрезвычайная широта теории множеств и ее приложимость к самым разным областям знания (математике, механике, физике, лингвистике, экономике и т. д.). Для математики особо важную роль играют множества, составленные из «математических» объектов— корней уравнений, геометрических фигур и т. д. Чаще всего нам будут встречаться числовые множества, то есть множества, элементами которых являются числа. Примерами числовых множеств являются: а) множество всех действительных чисел; б) множество всех рациональных чисел; в) множество всех положительных чисел; г) множество всех чисел, удовлетворяющих неравенству 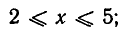
Некоторые числовые множества имеют особые названия. Если даны два числа а и b, а < b, то множество всех чисел, удовлетворяющих неравенству 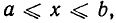
если это не вызывает недоразумений, просто отрезком и обозначают [а, b]. На числовой оси ему соответствует отрезок с концами а и b (рис. 1).
Множество чисел, удовлетворяющих неравенству а < х< b , называют числовым промежутком или, короче, промежутком и обозначают (а, b). На числовой оси ему соответствует отрезок, у которого отброшены концевые точки (рис. 2).
Множество чисел, удовлетворяющих неравенствам вида х > а (или х<а), называют (числовым) лучом. Его обозначают (а, 
(или (—
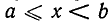
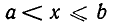
конец включается в множество, а круглая — что он исключается.
Пустое множество
Введение понятия множества в математику оказалось очень полезным. Из-за того что элементами множеств могут быть вещи самой различной природы, одни и те же утверждения, касающиеся множеств, можно истолковать и как утверждения о натуральных числах, и как утверждения о точках геометрических фигур, и как утверждения о множестве слов и т. д. Таким образом, понятия и теоремы теории множеств обладают большой общностью. Этим и объясняется то, что язык теории множеств применяется в самых различных областях математики.
В математике приходится иногда рассматривать множества, содержащие только один элемент, и даже множества, не имеющие ни одного элемента. Множество, не содержащее ни одного элемента, называют пустым. Его обозначают знаком 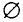
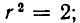
О некотором множестве может быть неизвестно, является ли оно пустым множеством или нет. Так, до сих пор неизвестно, пусто ли множество натуральных чисел n таких, что n > 2, а уравнение
имеет положительные целочисленные решения (в этом состоит известная проблема Ферма).
Пустое множество единственно: нет двух разных пустых множеств.
Подмножество
Пусть даны два множества A и B, причем каждый элемент первого множества является элементом второго множества. Тогда множество А называют подмножеством (или частью) множества В. В этом случае пишут:
Примеры подмножеств: а) числовой отрезок [1,3] есть подмножество числового отрезка [0, 4];
б) множество всех квадратов есть подмножество множества всех прямоугольников; в) множество всех целых чисел есть подмножество множества всех рациональных чисел.
Отметим, что пустое множество 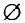
Множества часто изображают наглядно как множество точек геометрической фигуры. Тогда подмножество — это множество то чек части фигуры (рис. 5).
Пересечение множеств
Пусть даны множества А, В, С, … . Их пересечением называют множество X, содержащее те и только те элементы, которые входят в каждое из заданных множеств. Пере сечение двух множеств А и В обозначают АВ или
Если множества А и В состоят из точек некоторых геометрических фигур, то 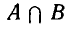
Пересечение множеств называют также их произведением, а операцию пересечения — умножением множеств. Можно показать,
что многие свойства пересечения множеств напоминают свойства умножения чисел.
Примеры пересечения множеств: а) пересечением числового отрезка [0, 4 ] с числовым отрезком [2, 5] является числовой отрезок [2, 4] (рис. 7);
б) пересечение числового отрезка [0, 2] с числовым отрезком [3, 5] пусто; в) пересечение множества всех ромбов с множеством всех прямоугольников есть множество всех квадратов; г) пересечением множества четных натуральных чисел с множеством натуральных чисел, делящихся на 3, является множество натуральных чисел, делящихся на 6.
Сложение множеств
Суммой (или объединением) множеств А, В, С, . . . называют множество X, состоящее из тех и только тех элементов, которые входят хотя бы в одно из этих («слагаемых») множеств. Сумму двух множеств А и В обозначают А + В или 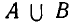
Если какой-нибудь элемент входит в несколько слагаемых множеств, то в сумме он берется лишь один раз. Например, суммой числового отрезка [0, 4] и числового отрезка [2, 5] является числовой отрезок [0, 5]. При этом точки отрезка [2, 4] входят в оба слагаемые, но в сумме они берутся лишь один раз. Впрочем, выражения «некоторый элемент берется в данном множестве пять раз» и т. п., как это следует из принятого нами понимания терминов «множество» и «элемент», просто не имеют смысла.
Примеры а) Обозначим через А множество точек некоторой плоской области и через В — множество точек другой области (рис. 8). Тогда их суммой будет множество точек заштрихованной фигуры, ограниченной на рис. 8 жирной линией. б) Обозначим через А множество успевающих учеников в классе, через В — множество девочек в этом классе и через С — множество неуспевающих мальчиков. Тогда 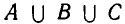
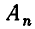
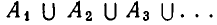
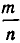
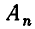
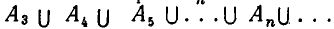
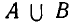
Разбиение множеств
Пусть множество X является суммой множеств A, В, С. . . , причем никакие два из них не имеют общих элементов. Тогда говорят, что множество X разбито на (непересекающиеся) подмножества А, В, С, . . . .
Примеры разбиения множеств: а) Множество натуральных чисел разбивается на подмножества четных чисел и нечетных чисел. б) Множество всех учеников в классе разбивается на множества учеников, фамилия которых начинается на букву «А», учеников, фамилия которых начинается на букву «Б», и т. д. вплоть до буквы «Я». Какое из этих множеств пусто, если взять ваш класс? Какие из этих множеств пусты для любого класса? в) Множество всех векторов на плоскости можно разбить на непересекающиеся подмножества, относя к одному подмножеству все векторы, равные друг другу по длине, параллельные и одинаково направленные. г) Это же множество можно разбить иначе, относя к одному под множеству векторы, выходящие из одной точки плоскости.
Вычитание множеств
Если даны два множества A и В, то их разностью называют такое множество X = A В или (А — В), в которое входят все элементы из Л, не принадлежащие множеству В. При этом не предполагается, что множество В является частью множества A. Таким образом, при вычитании множества В из множества A из A удаляют общую часть (пересечение) A и В:
Например, если A — множество всех учащихся IX класса данной школы, а В — множество всех девочек, которые учатся в этой школе, то A В — множество всех мальчиков, обучающихся в IX классе этой школы.
В случае, когда В — часть множества А, А В называют дополнением к В в множестве А и обозначают 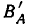
Отображение множеств
Пусть даны два множества X и У и пусть имеется правило 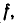
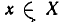
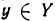
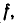
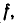
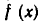
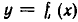
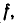
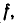

Если всякий 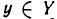
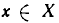



Приведем примеры отображений множеств: а) Пусть X — множество всех действительных чисел, У — множество всех неотрицательных чисел. Равенство 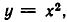
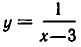
Пусть 
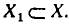
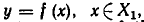
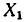

Рассмотрим некоторый элемент у из множества У и возьмем все элементы х из X, отображающиеся в у при отображении 

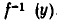
Если полный прообраз каждого элемента у из У при отображении 

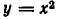
Если 

Краткие исторические сведения
Теоретико-множественные представления в неявной форме давно использовались математиками. Геометры древней Греции в III веке до н. э. рассматривали «геометрические места точек», то есть множества точек, обладающих тем или иным свойством. Однако трудности, связанные с понятием бесконечности, привели к тому, что в течение длительного времени математики избегали рассматривать геометрические фигуры как множества точек.
Исследования по бесконечным множествам начали чешский ученый Б. Больцано (1781— 1841) и немецкий математик Г. Кантор (родился в 1845 г. в Петербурге, умер в 1918 г. в Галле). Труд Больцано был опубликован лишь через много лет после его смерти. Основные заслуги в развитии теории множеств принадлежат Кантору. Он пришел к проблемам этой теории, исходя из сравнительно узкой математической задачи (вопроса о сходимости и расходимости тригонометрических рядов). Однако вскоре ему и его последователям стало ясно, что теория множеств имеет важнейшее значение для различных областей математики. Сейчас теория множеств дает общепринятый язык для многих разделов математики. В целом ряде случаев применение теоретико-множественных понятий позволило привести в систему многие ветви математики. Большой вклад в теорию множеств сделан трудами советских математиков П. С. Александрова, А. Н. Колмогорова, Н. Н. Лузина, П. С. Новикова, М. Я. Суслина и других. Советская школа теории множеств оказала сильное влияние на развитие этой части математики во всем мире.
Вскоре после создания теории множеств выяснилось, что «наивная» трактовка понятия бесконечного множества может привести к противоречиям. Исследования в этом направлении потребовали развития математической логики. Первоначально эта область математики была очень далека от практических приложений, но впоследствии ее принципы составили идейную основу конструирования электронных вычислительных машин и программирования вычислений на этих машинах.
Правила действий над высказываниями, во многом известные еще Аристотелю (создателю формальной логики), были более подробно сформулированы Г. В. Лейбницем, которого часто считают создателем математической логики. Алгебраическую форму этим правилам придали английские математика Дж. Буль (1815— 1864) и А. де Морган (1806—1871). По сути дела, эти правила совпадают с указанными выше правилами действий над множествами. Большой вклад в развитие математической логики внесли Г. Фреге, Б. Рассел, Д. Гильберт, К. Гёдель, А. Тарский, советские математики П. С. Новиков, А. Н. Колмогоров, А. А. Марков и другие.
Дополнение к различным типам множеств
Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Множества точек, задаваемые алгебраическими уравнениями и неравенствами
Числовые множества
Множества могут состоять из объектов самой различной природы. Их элементами могут быть буквы, атомы, книги, люди и т.д. Для математики особо важную роль играют множества, составленные из “математических” объектов – чисел, точек, геометрических фигур и т.п. Примерами числовых множеств являются:
а) множество всех действительных чисел R;
б) множество всех рациональных чисел Q;
в) множество всех натуральных чисел N;
г) множество всех чисел вида , где n принимает все натуральные значения.
В предлагаемой лекции мы рассмотрим примеры числовых множеств специального вида.
Множества точек на прямой
Числовые промежутки
Пример, имеющий важные применения, – соответствие между множеством действительных чисел R и множеством точек числовой прямой, т.е. прямой, на которой выбраны начало отсчета (ему сопоставлено число 0) и масштаб, однозначно определяющий равномерную шкалу. Каждой точке прямой соответствует ровно одно действительное число – координата этой точки, и обратно, каждому действительному числу x сопоставляется точка прямой с координатой x. Точка, соответствующая большему числу, находится правее, меньшему числу – левее. Данное соответствие позволяет множество чисел интерпретировать на геометрическом языке как множество точек прямой.
Интервалы
Открытым интерваломназывается множество всех чисел х, которые удовлетворяют неравенствам a x и x²
Заштрихованная часть числовой прямой содержит все точки, принадлежащие соответствующему интервалу. Незакрашенные кружочки означают, что эти точки не принадлежат интервалу, а закрашенные, наоборот, означают, что эти точки принадлежат интервалу.
Бесконечные интервалы.Интервал (–¥, a) (или (–¥, a]) – это множество всех чисел х, удовлетворяющих неравенству x a (или x ³ a). Интервал (–¥, +¥) – это множество R всех действительных чисел. Эти интервалы геометрически изображаются так:
Фигурирующие в этих обозначениях символы +¥ и –¥ ни в коем случае нельзя понимать как действительные числа. Наличие символа +¥ в обозначении интервала означает, что интервал содержит любые сколь угодно большие числа (например, интервал (а, +¥) содержит все числа, большие а). По аналогии с обычным интервалом можно записать, что интервал (а, +¥) состоит из всех чисел х – таких, что a a.
Точно так же наличие символа –¥ в обозначении интервала означает, что в этот интервал входят все отрицательные числа, абсолютные величины которых могут быть сколь угодно большими. Неравенство x > –¥, равно как и неравенство –¥
Пример.Пусть A, B, C – множества действительных чисел: A = (–4, 7); B = [0, 10], C = [–1, 4). Числовые промежутки A, B, C изображены на рисунке 3. Светлыми кружками обозначены концы промежутка, не принадлежащие ему (так, у интервала оба конца – светлые); закрашенными – принадлежащие промежутку.
A ∩ B = [0, 7); A È B = (–4, 10]; A B = (–4, 0); B A = [7, 10]; C A = Æ; A C = (–4, –1) È [4, 7).
Упражнение. Покажите на числовой прямой множества B ∩ C, B È C, B C, C B, A ∩ C,
A È C , , , и представьте эти промежутки с помощью введенных выше обозначений.
Замечание. Следует отметить, что одинаковым образом определяются и обозначаются числовые промежутки как в области действительных чисел (и тогда промежуток содержит бесконечное множество чисел), так и в области целых чисел (тогда, например, целочисленный отрезок [–3, 2] содержит 6 чисел: <–3, –2, –1, 0, 1, 2>, а интервал (–3, 2) содержит 4 числа:
<–2, –1, 0, 1>. Разница определяется тем, какое множество выбрано в качестве универсального
Множества точек, задаваемые алгебраическими уравнениями и неравенствами
С каждым уравнением связаны два числовых множества. Первое из них – область определения уравнения. Это множество состоит из всех значений х, для которых имеют смысл обе части уравнения. Второе множество – это множество его корней, то есть чисел, при подстановке которых в уравнение оно обращается в тождество.
Пример 1. Уравнение имеет своей областью определения множество [–4, +¥). Найдем его корни. Возведем обе части уравнения в квадрат:
Решим полученное квадратное уравнение:
Оба числа x1 = 0 и x2 = 5 принадлежат множеству [–4, +¥), однако число x2 = 5 является посторонним корнем уравнения (это показывает простая проверка: ). Таким образом, множество корней данного уравнения <0>Ì [–4, +¥). На прямой эти множества изображаются так:
Пример 2. Уравнение |x| = 3 имеет своей областью определения множество (–¥, +¥). Найдем его корни. По определению абсолютной величины числа х имеем
.
Поэтому данное уравнение можно представить в виде совокупности двух уравнений: х = 3 и
–х = 3. Откуда получим два корня: x1 = 3, x2 = –3. Геометрически эти решения можно истолковать так: расстояние от x1 до начала отсчета О и расстояние x2 до начала отсчета О равны 3 (рисунок 4).
Пример 3. Неравенство |x| 3 имеет своими решениями объединение двух множеств:
(–¥, –3) È (3, +¥). Геометрически условие |x| > 3 означает, что расстояние от точки х до начала отсчета больше 3. Множество решений этого неравенства изображено на рисунке 7.
В случае неравенства |x – x0| 0, множество решений имеет вид (x0 – a, x0 + a) и является открытым интервалом длины 2а с центром в точке (рисунок 8).
Множество решений неравенства |x – x0| > a, где a > 0, представляет собой объединение двух множеств (–¥, x0 – a) È (x0 + a, +¥). Эти множества изображены на рисунке 9.
Операции над множествами
Пересечение множеств
Рассмотрим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Видим, что Том и Фред одновременно являются друзьями Джона и Майкла.
Говоря на языке множеств, элементы Том и Фред принадлежат как множеству друзей Джона, так и множеству друзей Майкла.
Зададим новое множество с названием «Общие друзья Джона и Майкла» и в качестве элементов добавим в него Тома и Фреда :
| Общие друзья Джона и Майкла | = |
В данном случае множество «Общие друзья Джона и Майкла» является пересечением множеств друзей Джона и Майкла.
Пересечением двух (или нескольких) исходных множеств называется множество, которое состоит из элементов, принадлежащих каждому из исходных множеств.
В нашем случае элементы Том и Фред принадлежат каждому из исходных множеств, а именно: множеству друзей Джона и множеству друзей Майкла.
Обозначим множество друзей Джона через букву A , множество друзей Майкла — через букву B , а множество общих друзей Джона и Майкла обозначим через букву C :
Тогда пересечением множеств A и B будет множество C и записываться следующим образом:
Символ ∩ означает пересечение.
Говоря о множестве, обычно подразумевают элементы, принадлежащие этому множеству. Символ пересечения ∩ читается, как союз И. Тогда выражение A ∩ B = C можно прочитать следующим образом:
«Элементы, принадлежащие множеству A И множеству B, есть элементы, принадлежащие множеству C».
«Друзья, одновременно принадлежащие Джону И Майклу, есть общие друзья Джона и Майкла».
Теперь представим, что у Джона и Майкла нет общих друзей. Для удобства, как и прежде обозначим множество друзей Джона через букву A , а множество друзей Майкла через букву B
В этом случае говорят, что исходные множества не имеют общих элементов и пересечением таких множеств является пустое множество. Пустое множество обозначается символом ∅
Пример 2. Рассмотрим два множества: множество A , состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Множество С является пересечением множеств A и B , поскольку элементы множества C одновременно принадлежат множеству A и множеству B
Пример 3. Рассмотрим два множества: множество A, состоящее из чисел 1, 5, 7, 9 и множество B , состоящее из чисел 1, 4, 5, 7
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Множество С является пересечением множеств A и B , поскольку элементы множества C одновременно принадлежат множеству A и множеству B.
Пример 4. Найти пересечение следующих множеств:
Пересечением множеств A , B и C будет множество, состоящее из элементов, принадлежащих каждому из множеств A , B и C . Этими элементами являются числа 3 и 9.
Зададим новое множество D и добавим в него элементы 3 и 9. Затем с помощью символа пересечения ∩ запишем, что пересечением множеств A, B и C является множество D
Чтобы найти пересечение, вовсе необязательно задавать множества с помощью букв. Если элементов мало, то множество можно задать прямым перечислением элементов.
К примеру, пусть первое множество состоит из элементов 1, 3, 5, а второе из элементов 2, 3, 5 . Пересечением в данном случае является множество, состоящее из элементов 3 и 5 . Чтобы записать пересечение, можно воспользоваться прямым перечислением:
Числовые промежутки, которые мы рассмотрели в предыдущих уроках, тоже являются множествами. Элементами таких множеств являются числа, входящие в числовой промежуток.
Например, отрезок [2; 6] можно понимать, как множество всех чисел от 2 до 6. Для наглядности можно перечислить все целые числа, принадлежащие данному отрезку:
Следует иметь ввиду, что мы перечислили только целые числа. Отрезку [2; 6] также принадлежат и другие числа, не являющиеся целыми, например, десятичные дроби. Десятичные дроби располагаются между целыми числами, но их количество настолько велико, что перечислить их не представляется возможным.
Еще пример. Интервал (2; 6) можно понимать, как множество всех чисел от 2 до 6, кроме чисел 2 и 6. Ранее мы говорили, что интервал это такой числовой промежуток, границы которого не принадлежат ему. Для наглядности можно перечислить все целые числа, принадлежащие интервалу (2; 6) :
Поскольку числовые промежутки являются множествами, то мы можем находить пересечения между различными числовыми промежутками. Рассмотрим несколько примеров.
Пример 5. Даны два числовых промежутка: [2; 6] и [4; 8] . Найти их пересечение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [2; 6] и [4; 8] :
Видно, что числа 4, 5, 6 принадлежат как первому промежутку [2; 6] , так и второму [4; 8] .
Тогда пересечением числовых промежутков [2; 6] и [4; 8] будет числовой промежуток [4; 6]
Изобразим промежутки [2; 6] и [4; 8] на координатной прямой. На верхней области отметим числовой промежуток [2; 6] , на нижней — промежуток [4; 8]
Видно, что числа, принадлежащие промежутку [4; 6] , принадлежат как промежутку [2; 6] , так и промежутку [4; 8] . Можно также заметить, что штрихи, входящие в промежутки [2; 6] и [4; 8] пересекаются в промежутке [4; 6] . В такой ситуации, когда перед глазами есть координатная прямая, понятие пересечения множеств можно понимать в прямом смысле, что очень удобно.
Пример 6. Найти пересечение числовых промежутков [−2; 3] и [4; 7]
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [−2; 3] и [4; 7] :
−2, −1, 0, 1, 2, 3 ∈ [−2; 3]
Видно, что числовые промежутки [−2; 3] и [4; 7] не имеют общих чисел. Поэтому их пересечением будет пустое множество:
Если изобразить числовые промежутки [−2; 3] и [4; 7] на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Пример 7. Дано множество из одного элемента < 2 >. Найти его пересечение с промежутком (−3; 4)
Множество, состоящее из одного элемента < 2 >, на координатной прямой изображается в виде закрашенного кружка, а числовой промежуток (−3; 4) это интервал, границы которого не принадлежат ему. Значит границы −3 и 4 будут изображаться в виде пустых кружков:
Пересечением множества < 2 >и числового промежутка (−3; 4) будет множество, состоящее из одного элемента < 2 >, поскольку элемент 2 принадлежит как множеству < 2 >, так и числовому промежутку (−3; 4)
На самом деле мы уже занимались пересечением числовых промежутков, когда решали системы линейных неравенств. Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
По сути, множество решений, удовлетворяющих обоим неравенствам, является пересечением множеств решений первого и второго неравенства. Роль этих множеств берут на себя числовые промежутки.
Например, чтобы решить систему неравенств , мы должны сначала найти множества решений каждого неравенства, затем найти пересечение этих множеств.
В данном примере решением первого неравенства x ≥ 3 является множество всех чисел, которые больше 3 (включая само число 3). Иначе говоря, решением неравенства является числовой промежуток [3; +∞)
Решением второго неравенства x ≤ 6 является множество всех чисел, которые меньше 6 (включая само число 6). Иначе говоря, решением неравенства является числовой промежуток (−∞; 6]
А общим решением системы будет пересечение множеств решений первого и второго неравенства, то есть пересечение числовых промежутков [3; +∞) и (−∞; 6]
Если мы изобразим множество решений системы на координатной прямой, то увидим, что эти решения принадлежат промежутку [3; 6] , который в свою очередь является пересечением промежутков [3; +∞) и (−∞; 6]
Поэтому в качестве ответа мы указывали, что значения переменной x принадлежат числовому промежутку [3; 6], то есть пересечению множеств решений первого и второго неравенства
Пример 2. Решить неравенство
Все неравенства, входящие в систему уже решены. Нужно только указать те решения, которые являются общими для всех неравенств.
Решением первого неравенства является числовой промежуток (−∞; −1) .
Решением второго неравенства является числовой промежуток (−∞; −5) .
Решением третьего неравенства является числовой промежуток (−∞; 4) .
Решением системы будет пересечение числовых промежутков (−∞; −1), (−∞; −5) и (−∞; 4) . В данном случае этим пересечением является промежуток (−∞; −5) .
На рисунке представлены числовые промежутки и неравенства, которыми эти числовые промежутки заданы. Видно, что числа, принадлежащие промежутку (−∞; −5) , одновременно принадлежат всем исходным промежуткам.
Запишем ответ к системе с помощью числового промежутка:
Пример 3. Решить неравенство
Решением первого неравенства y > 7 является числовой промежуток (7; +∞) .
Решением второго неравенства y является числовой промежуток (−∞; 4) .
Решением системы будет пересечение числовых промежутков (7; +∞) и (−∞; 4) .
В данном случае пересечением числовых промежутков (7; +∞) и (−∞; 4) является пустое множество, поскольку эти числовые промежутки не имеют общих элементов:
Если изобразить числовые промежутки (7; +∞) и (−∞; 4) на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Объединение множеств
Объединением двух (или нескольких) исходных множеств называют множество, которое состоит из элементов, принадлежащих хотя бы одному из исходных множеств.
На практике объединение множеств состоит из всех элементов, принадлежащих исходным множествам. Поэтому и говорят, что элементы такого множества принадлежат хотя бы одному из исходных множеств.
Рассмотрим множество A с элементами 1, 2, 3 и множество B с элементами 4, 5, 6.
Зададим новое множество C и добавим в него все элементы множества A и все элементы множества B
В данном случае объединением множеств A и B является множество C и обозначается следующим образом:
Символ ∪ означает объединение и заменяет собой союз ИЛИ. Тогда выражение A ∪ B = C можно прочитать так:
Элементы, принадлежащие множеству A ИЛИ множеству B, есть элементы, принадлежащие множеству C.
В определении объединения сказано, что элементы такого множества принадлежат хотя бы одному из исходных множеств. Данную фразу можно понимать в прямом смысле.
Вернёмся к созданному нами множеству C , куда входят все элементы множеств A и B . Возьмём для примера из этого множества элемент 5. Что можно про него сказать?
Если 5 является элементом множества C , а множество С является объединением множеств A и B , то можно с уверенностью заявить, что элемент 5 принадлежит хотя бы одному из множеств A и B . Так оно и есть:
Возьмем ещё один элемент из множества С , например, элемент 2. Что можно про него сказать?
Если 2 является элементом множества C , а множество С является объединением множеств A и B , то можно с уверенностью заявить, что элемент 2 принадлежит хотя бы одному из множеств A и B . Так оно и есть:
Если мы захотим объединить два или более множества и вдруг обнаружим, что один или несколько элементов принадлежат каждому из этих множеств, то в объединение повторяющиеся элементы будут входить только один раз.
Например, рассмотрим множество A с элементами 1, 2, 3, 4 и множество B с элементами 2, 4, 5, 6.
Видим, что элементы 2 и 4 одновременно принадлежат и множеству A , и множеству B . Если мы захотим объединить множества A и B , то новое множество C будет содержать элементы 2 и 4 только один раз. Выглядеть это будет так:
Чтобы при объединении не допустить ошибок, обычно поступают так: сначала в новое множество добавляют все элементы первого множества, затем добавляют элементы второго множества, которые не принадлежат первому множеству. Попробуем сделать такое объединение с множествами A и B .
Итак, у нас имеются следующие исходные множества:
Зададим новое множество С и добавим в него все элементы множества A
Теперь добавим элементы из множества B , которые не принадлежат множеству A . Множеству A не принадлежат элементы 5 и 6 . Их и добавим во множество C
Пример 2. Друзьями Джона являются Том, Фред, Макс и Джордж. А друзьями Майкла являются Лео, Том, Фред и Эван. Найти объединение множеств друзей Джона и Майкла.
Для начала зададим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Зададим новое множество с названием «Все друзья Джона и Майкла» и добавим в него всех друзей Джона и Майкла.
Заметим, что Том и Фред одновременно являются друзьями Джона и Майкла, поэтому мы добавим их в новое множество только один раз, поскольку сразу двух Томов и двух Фредов не бывает.
| Все друзья Джона и Майкла | = |
В данном случае множество всех друзей Джона и Майкла является объединением множеств друзей Джона и Майкла.
Друзья Джона ∪ Друзья Майкла = Все друзья Джона и Майкла
Пример 3. Даны два числовых промежутка: [−7; 0] и [−3; 5] . Найти их объединение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие этим промежуткам:
−7, −6, −5, −4, −3,−2, −1 , 0 ∈ [−7; 0]
−3,−2, −1 , 0, 1, 2, 3, 4, 5 ∈ [−3; 5]
Объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5] , который содержит все числа промежутка [−7; 0] и [−3; 5] без повторов некоторых из чисел
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Обратите внимание, что числа −3,−2, −1 принадлежали и первому промежутку и второму. Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Значит объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5]
Изобразим на координатной прямой промежутки [−7; 0] и [−3; 5] . На верхней области отметим числовой промежуток [−7; 0] , на нижней — промежуток [−3; 5]
Ранее мы выяснили, что промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5] . Здесь полезно вспомнить про определение объединения множеств, которое было приведено в самом начале. Объединение трактуется, как множество, состоящее из всех элементов, принадлежащих хотя бы одному из исходных множеств.
Действительно, если взять любое число из промежутка [−7; 5] , то окажется, что оно принадлежит хотя бы одному из промежутков: либо промежутку [−7; 0] либо промежутку [−3; 5] .
Возьмём из промежутка [−7; 5] любое число, например число 2 . Поскольку промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5] , то число 2 будет принадлежать хотя бы одному из этих промежутков. В данном случае число 2 принадлежит промежутку [−3; 5]
Возьмём ещё какое-нибудь число. Например, число −4 . Это число будет принадлежать хотя бы одному из промежутков: [−7; 0] или [−3; 5] . В данном случае оно принадлежит промежутку [−7; 0]
Возьмём ещё какое-нибудь число. Например, число −2 . Оно принадлежит как промежутку [−7; 0] , так и промежутку [−3; 5] . Но на координатной прямой оно указывается только один раз, поскольку в одной точке сразу два числа −2 не бывает.
Не каждое объединение числовых промежутков является числовым промежутком. Например, попробуем найти объединение числовых промежутков [−2 ; −1] и [4 ; 7].
Идея остаётся та же самая — объединением числовых промежутков [−2 ;−1] и [4 ; 7] будет множество, состоящее из элементов, принадлежащих хотя бы одному из промежутков: [−2; −1] или [4; 7] . Но это множество не будет являться числовым промежутком. Для наглядности перечислим все целые числа, принадлежащие этому объединению:
Получили множество < −2, −1, 4, 5, 6, 7 >. Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4 , не вошли в полученное множество
Числовой промежуток должен содержать все числа от левой границы до правой. Если одно из чисел отсутствует, то числовой промежуток теряет смысл. Допустим, имеется линейка длиной 15 см
Эта линейка является числовым промежутком [0; 15], поскольку содержит все числа в промежутке от 0 до 15 включительно. Теперь представим, что на линейке после числа 9 сразу следует число 12.
Эта линейка не является линейкой в 15 см, и её нежелательно использовать для измерения. Также, её нельзя назвать числовым промежутком [0; 15] , поскольку она не содержит все числа, которые должна была содержать.
Решение неравенств, содержащих знак ≠
Некоторые неравенства содержат знак ≠ (не равно). Например, 2x ≠ 8 . Чтобы решить такое неравенство, нужно найти множество значений переменной x , при которых левая часть не равна правой части.
Решим неравенство 2x ≠ 8 . Разделим обе части данного неравенства на 2, тогда получим:
Получили равносильное неравенство x ≠ 4 . Решением этого неравенства является множество всех чисел, не равных 4. То есть если мы подставим в неравенство x ≠ 4 любое число, которое не равно 4, то получим верное неравенство.
Подставим, например, число 5
5 ≠ 4 — верное неравенство, поскольку 5 не равно 4
7 ≠ 4 — верное неравенство, поскольку 7 не равно 4
И поскольку неравенство x ≠ 4 равносильно исходному неравенству 2x ≠ 8 , то решения неравенства x ≠ 4 будут подходить и к неравенству 2x ≠ 8 . Подставим те же тестовые значения 5 и 7 в неравенство 2x ≠ 8 .
Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:
Теперь запишем ответ в виде числового промежутка. Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞) . Напомним, что для слова «или» используется символ ∪
В этом выражении говорится, что значения, принимаемые переменной x , принадлежат промежутку (−∞; 4) или промежутку (4; +∞).
Неравенства, содержащие знак ≠ , также можно решать, как обычные уравнения. Для этого знак ≠ заменяют на знак = . Тогда получится обычное уравнение. В конце решения найденное значение переменной x нужно исключить из множества решений.
Решим предыдущее неравенство 2x ≠ 8 , как обычное уравнение. Заменим знак ≠ на знак равенства = , получим уравнение 2x = 8 . Разделим обе части данного уравнения на 2 , получим x = 4 .
Видим, что при x , равном 4, уравнение обращается в верное числовое равенство. При других значениях равенства соблюдаться не будет. Эти другие значения нас и интересуют. А для этого достаточно исключить найденную четвёрку из множества решений.
Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x
Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 5
Решением неравенства x ≠ 1,2 является множество всех чисел, не равных 1,2 .
Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:
В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)
Решение совокупностей неравенств
Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.
А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.
Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:
Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.
Решением первого неравенства x ≥ 3 является числовой промежуток [3; +∞) . Решением второго неравенства x ≤ 6 является числовой промежуток (−∞; 6] .
Множество значений x , при которых верно хотя бы одно из неравенств, будет принадлежать промежутку [3; +∞) или промежутку (−∞; 6] . Так и записываем:
В этом выражении говорится, что переменная x , входящая в
совокупность принимает все значения, принадлежащие промежутку [3; +∞) или промежутку (−∞; 6] . А это то, что нам нужно. Ведь решить совокупность означает найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность. А любое число из промежутка [3; +∞) или промежутка (−∞; 6] будет удовлетворять хотя бы одному неравенству.
Например, число 9 из промежутка [3; +∞) удовлетворяет первому неравенству x ≥ 3. А число −7 из промежутка (−∞; 6] удовлетворяет второму неравенству x ≤ 6.
Посмотрите внимательно на выражение x ∈ [3; +∞) ∪ (−∞; 6], а именно на его правую часть. Ведь выражение [3; +∞) ∪ (−∞; 6] представляет собой объединение числовых промежутков [3; +∞) и (−∞; 6] . Точнее, объединение множеств решений первого и второго неравенства.
Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности будет объединение числовых промежутков [3; +∞) и (−∞; 6]
Объединением числовых промежутков [3; +∞) и (−∞; 6] является промежуток (−∞; +∞) . Точнее, объединением числовых промежутков [3; +∞) и (−∞; 6] является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.
Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.
Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6
Возьмем еще какое-нибудь число, например, число 5 . Оно удовлетворяет и первому неравенству x ≥ 3 и второму x ≤ 6
Пример 2. Решить совокупность неравенств
Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.
Для начала найдём множество решений первого неравенства x . Этим множеством является числовой промежуток (−∞; −0,25) .
Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).
Решением совокупности неравенств будет объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности будет объединение числовых промежутков (−∞; −0,25) и [−7; +∞)
Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Пример 3. Решить совокупность неравенств
Решим каждое неравенство по отдельности:
Множеством решений первого неравенства x является числовой промежуток (−∞; −3) .
Множеством решений второго неравенства x ≤ 0 является числовой промежуток (−∞; 0] .
Решением совокупности неравенств будет объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности будет объединение числовых промежутков (−∞; −3) и (−∞; 0]
Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]
Ответ можно оставить таким, каким мы его записали ранее:
Урок на тему «Метод областей». 11-й класс
Класс: 11
Презентация к уроку
«Считай несчастным тот день и тот час,
вк оторый ты не усвоил ничего нового и ничего
не прибавил к своему образованию».
Я.А Коменский
Тип урока: урок-обобщения и систематизации знаний учащихся.
Цели урока:
- создать условия для систематизации, обобщения знаний и умений обучающихся по применению различных методов решения неравенств;
- воспитание нравственных качеств личности, таких как ответственность, аккуратность, дисциплинированность;
- воспитание культуры общения.
- развитие у учащихся умений выделять главное, существенное в изучаемом материале, обобщать изучаемые факты, логически излагать свои мысли;
- развитие психических процессов, таких как память, внимание, мышление, а также наблюдательности, активности, самостоятельности.
Задачи:
- формировать умение классифицировать неравенства по методам решения;
- закрепить навыки решения неравенств различными методами;
- отрабатывать навыки самоконтроля с целью подготовки к итоговой аттестации;
- воспитывать чувство коллективизма, ответственности.
Оборудование:
- Компьютер
- Мультимедийный проектор, звуковые колонки
- Программа «MicrosoftPowerPoint 2003»
Методы обучения:
- частично-поисковый метод,
- репродуктивный,
- обобщающий.
План урока.
План урока рассчитан на 2 учебных часа (90 мин)
- Организационный момент.
- Вступительное слово учителя.
- Повторение теории.
- Решение неравенств различными методами (варианты ЕГЭ)
- Самостоятельная работа с самопроверкой.
- Итог урока.
- Рефлексия.
Ход урока
I. Организационный момент
«То, что мы знаем, — ограничено, а то чего
мы не знаем, — бесконечно».
Приветствие учащихся.Ученики под руководством учителя проверяют наличие дневника, рабочей тетради, инструментов, отмечаются отсутствующие, проверяется готовность класса к уроку, учитель психологически настраивает детей на работу на уроке.Формулируется тема и цели урока. Знакомство с этапами урока.
II. Вступительное слово учителя
Для успешного исследования многих задач повышенной сложности полезно уметь строить не только графики функций, но и множества точек плоскости, координаты которых удовлетворяют заданным уравнениям, неравенствам или их системам. Эффективно строить на координатной плоскости такие множества позволяет метод областей. Это весьма полезный прием можно назвать обобщающим методом интервалов.
Метод областей особенно полезен при решении уравнений или неравенств с параметром. Применение метода интервалов в таких случаях затруднено, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра. Это означает необходимость сравнивать их между собой и рассматривать различные случаи. В этой ситуации нам может помочь метод областей.
III. Повторение теории
Метод интервалов на координатной прямой и метод областей на координатной плоскости.
Точка х=а разбивает числовую прямую на два множества, задаваемые неравенствами x a
Всякая действительная кривая на координатной плоскости, заданная уравнением F(x;y)=0 разбивает координатную плоскость на конечное число областей, в каждой из которых для всех точек области выполняется только одно из неравенств: F(x;y)>0 или F(x;y) kx+p или y c
Решением системы неравенств с двумя переменными являются координаты точек пересечения множеств, удовлетворяющих одному из неравенств системы
Уравнение y= k(x-x0) + y0 задает множество прямых, проходящих через точку с координатами (x0,y0).
При изменении значений параметра прямые y= k(x-x0) + y0 «поворачиваются» вокруг данной точки. При увеличении параметра прямая поворачивается «против часовой стрелки», при уменьшении – «по часовой стрелке».
Уравнение y=kx+p при фиксированном значении параметра k = k0 задает семейство прямых, параллельных прямой y=kx+p проходящей через начало координат
Если точка с координатами лежит «выше» прямой заданной уравнением y=kx+p, то ее координаты удовлетворяют неравенству , если же точка лежит «ниже», то неравенству
Задача
Пусть M – множество точек плоскости с координатами (x; y) таких, что числа x, y, 6-2x являются сторонами некоторого треугольника. Найдите его площадь.
Если три числа являются сторонами некоторого треугольника, то это числа положительные и каждое из них меньше суммы двух других чисел. Поэтому, координаты точек, удовлетворяющих условию задачи, будут задаваться системой линейных неравенств с двумя переменными:
Геометрическое место точек на плоскости
Множество точек плоскости, равноудаленных от данной точки на расстояние, равное положительной величине R, называется окружностью.
Уравнением окружности называется уравнение вида
Множество точек, удаленных от данной точки на положительное расстояние, меньшее R, называется кругом. Круг задается неравенством
Множество точек, лежащих вне круга, задается неравенством
Геометрическое место точек на плоскости
Квадратным трехчленом относительно переменной, называется выражение
Графиком квадратного трехчлена является кривая, называемая параболой.
Расположение параболы зависит от знака старшего коэффициента и знака дискриминанта квадратного трехчлена
Парабола разбивает плоскость на часть, лежащую «над» параболой и лежащую «под» параболой. Первая задается неравенством
, а вторая –
Метод областей при решении задач с параметрами
1. Свойства функций
2. Графический прием
Параметр – «равноправная» переменная Þ отведем ему координатную ось, т.е. задачу с параметром будем рассматривать как функцию f(x ;a) >0
Общие признаки задач подходящих под рассматриваемый метод:
- В задаче дан один параметр а и одна переменная х
- Они образуют некоторые аналитические выражения F(x;a), G(x;a)
- Графики уравнений F(x;a)=0,G(x;a)=0 строятся несложно
- Строим графический образ
- Пересекаем полученный график прямыми, перпендикулярными параметрической оси
- «Считываем» нужную информацию
Обобщенный метод областей («переход» метода интервалов с прямой на плоскость)
Неравенства с одной переменной
Неравенства с двумя переменной
- ОДЗ
- Граничные линии
- Координатная плоскость
- Знаки в областях
- Ответ по рисунку
IV. Решение неравенств
Пример №1
Найти все значения параметра p, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства
Применим обобщенный метод областей.
1. Построим граничные линии
2. Определяем знаки в полученных областях и получаем решение 1 неравенства
3. Из полученного множества исключим решение
Пример № 2
При каких значениях параметра а система неравенств не имеет решений.
1. Рассмотрим 1 неравенство и получаем
2. Рассмотрим 2 неравенство и получаем
3. Заметим, что исходная система неравенств равносильна системе:
4. Изобразим систему неравенств в виде плоской фигуры на координатной плоскости. Для этого введём параметрическую плоскость Oax
5. Мы получили плоскую фигуру, множество точек которой является решением системы.
Таким образом, отвечая на вопрос задачи, решений системы нет при
Пример №3
При каких положительных значениях параметраа система уравнений имеет ровно 4 решения.
1. Запишем систему в следующем виде:
2. Построим график 1 уравнения.
3. Построим график 2 уравнения – семейство окружностей с центром в точке (2; 0) и радиусом а.
Ответ: при
V. Самостоятельная работа с самопроверкой
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству
1. ОДЗ:
2. Строим граничные линии:
3. Они разбивают плоскость на восемь областей, определяя знаки подстановкой в отдельных точках, получаем решение.
Ответ: заштрихованная область на рисунке
На координатной плоскости изобразите множество точек, координаты которых удовлетворяют неравенству
- На координатной плоскости нарисуем линии определённые равенствами x-y=0 и xy-1=0, которые разбивают плоскость на несколько областей.
- Определяем знаки в областях.
Ответ: заштрихованная область на рисунке
VI. Итог урока
(подвожу итог, комментирую работу учащихся, сообщаю оценки за урок.)
VII. Рефлексия.
Ребята. На этом урок окончен. Спасибо за урок!
Литература.
- П. И. Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. 3-е издание, дополненное и переработанное. — М.: Илскса, Харьков: Гимназия, 2005,- 328 с.
- Черкасов О. Ю., Якушев А. Г. Математика: интенсивный курс подготовки к экзамену.
- Экзаменационные материалы для подготовки к ЕГЭ-2007. Математика. М.: ООО «РУСТЕСТ», 2006. — 108с. Сост. — Клово А.Г.
- Задачи с параметром и другие сложные задачи. Козко А.И., Чирский В.Г. М.: МЦНМО, 2007. — 296с.
- ЕГЭ 2011. Математика. Задача С5. Козко А.И., Панферов В.С., Сергеев И.Н., Чирский В.Г.
http://urok.1sept.ru/articles/664756
Решение некоторых математических задач предусматривает операции над множествами такие как пересечение, объединение, разность. Под множеством подразумевают объединение некоторых предметов в одно целое. Для совершения подобных действий требуется знание некоторых правил, которые позволят найти пересечение, объединение и разность множеств. О таких правилах пойдёт речь далее.
Обозначение множеств. Как записать объединение и пересечение множеств
Определения
Объединение множеств – это ряд таких элементов, при которым каждый из них представляет собой элемент одного из первоначальных множеств.
Пересечение множеств — заключает в себе все элементы, общие для первоначальных множеств.
При записи обозначения пересечения множеств и объединения множества чисел, используют специальный порядок символов. Самый лёгкий способ обозначить множество — это применение фигурных скобок, в середине которых элементы записаны через запятую.
А = {7, 3, 15, 31}
С помощью такой записи можно задать множество, если оно включает небольшое конечное число элементов. В связи с этим чаще применяется многофункциональный способ определения множеств – посредством характеристического свойства, которое свойственно всем элементам множества, которым не владеют объекты вне множества.
A = {x | P(x)} или A = {x : P(x)}
P(x) – характеристическое свойство множества A.
В таком виде объединение записывается следующим образом:
AUB={x|xєAvxєB}
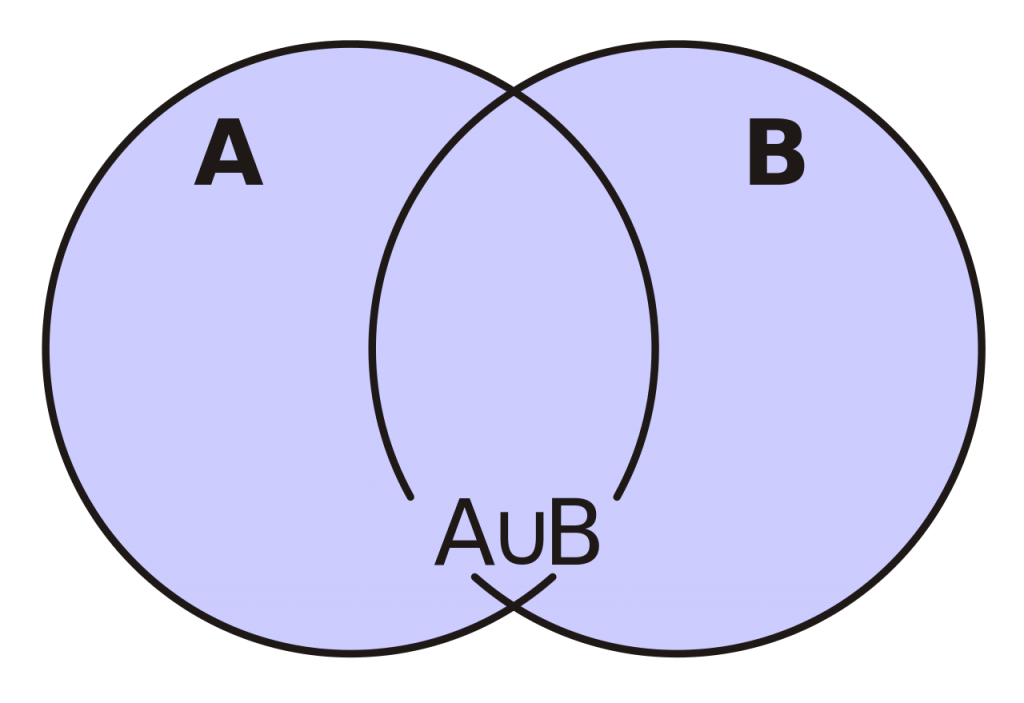
а пересечение множеств записывается как:
AՈB={x|xєAᴧxєB}
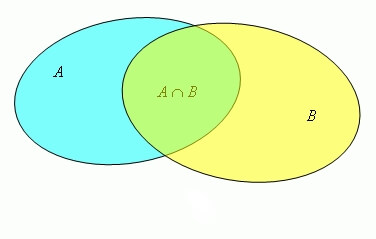
Где символы v / ᴧ, обозначают «или» / «и», символ | обозначает «таких что».
Чтобы обозначить множества, как числовые интервалы, при записи применяют скобки круглой и квадратной формы. К примеру, запись [4,24), выражает цифровой диапазон от 4 до 24, при этом число 4 входит в состав множества, а 24 нет. Числа менее 24 принадлежат этому множеству.
Найти пересечение и объединение множеств. Операции над множествами
Важно
U – обозначает объединение множеств A и B;
Ո – обозначает пересечение множеств A и B.
Чтобы легче запомнить данные знаки пересечения и объединения множеств, можно мысленно представить, что символ объединения U напоминает сосуд с открытым верхом, туда есть возможность что-то положить.
Символ пересечения Ո наоборот, выглядит как перевёрнутая ёмкость, в который невозможно поместить какой-либо предмет. Так же символ обозначающий пересечение Ո можно прочитать как «И».
Тогда выражение AՈB=C, читается так: “Все элементы, входящие в состав множества A и множества B, составляют элементы, которые принадлежат множеству C».
Правила нахождения объединения и пересечения и разности множеств
При формировании объединения числовых множеств, следует последовательно записать полностью части одного множества и их дополнить недостающими элементами из остальных. Операцию объединения в отдельных случаях называют сложением множеств и обозначают знаком «+».
Рассмотрим пример объединения числовых множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10}. К имеющимся числовым составляющим множества A 1,2,3,4,5,6,7,8,9 прибавим недостающую часть из множества B 10. Получившееся в результате объединения множество чисел будет выглядеть так {0,1,2,3,4,5,6,7,8,9,10}. Соответственно запись этого объединения:
AUB={0,1,2,3,4,5,6,7,8,9,10}
Чтобы составить пересечение числовых множеств, следует последовательно выбирать части одного множества и удостовериться, входят ли они в другие исследуемые множества, входящие в их число и составляют пересечение.
Для того, чтобы найти пересечение этих же множеств, друг за другом, последовательно проанализируем числа множества A на их наличие в множестве чисел B. Начнём проверку с самого первого числа в множестве A это число 0. В множестве B данное число отсутствует и не войдёт в совокупность пересечения. Смотрим далее, число 1 из множества A так же имеется в составе множества B. Затем следует число 2, которое принадлежит множеству B и, следовательно, пересечению. Идущее за ним 3 не принадлежит A и B не входит в перечисление. Число 4 входит в A и B, значит войдёт и в объединение. Далее продолжаем проверять числа по аналогии. Итак, пересечение множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10} состоит из чисел 2,4,6,8. При записи выглядит так:
AՈB={2,4,6,8}
Выполнение записи пересечения и объединения нескольких множеств
Если требуется выполнить операции с более чем двумя множествами, например: A, B, C, принцип действия подобный предыдущим примерам. В первую очередь находим пересечения A и B. Только затем пересечение полученного множества с C.
Следовательно, процесс нахождения пересечения более двух множеств осуществляется в несколько этапов.
Например, дано три множества A = {1,2,3,7,9}, B = {1,3,5,7,9} и C = {3,4,5,8,9}. Сначала находим пересечение AՈB = {3,9}, затем сравниваем полученное множество с C, это будут те же 3 и 9. Получаем, что пересечение A, B, C выглядит следующим образом:
AՈBՈC={3,9}
При определении объединений двух и более множеств, к числам первого множества последовательно добавляют отсутствующие элементы из второго, третьего и последующих множеств. К примеру, даны следующее множества A = {1,4}, B = {4,3,} и C = {1,3,6,7}. К числовым элементам 1 и 4 из множества A, прибавляем число 4 из множества B. Теперь, к получившемуся множеству 1,3,4 прибавляем цифры 6 и 7 из множества C. В конечном результате получаем объединение:
AUBUC = {1,3,4,6,7}
Для нахождения пересечения совсем не нужно писать много букв. Когда элементов не много, то множество возможно задать элементарным перечислением. Например, первое множество включает в себя числа 1,3,5, второе состоит из элементов 2,3,5. В данном случае, пересечение будет состоять из элементов 3 и 5. Для записи можно использовать прямое перечисление: {1,3,5} Ո {2,3,5} = {3,5}
Основные свойства объединения и перечисления множеств
- Коммутативность или перестановка. Распространяется на все компоненты при любом их количестве.
- AUB = BUA
- AՈB = BՈA
- Ассоциативность или расстановка скобок. Позволяет опускать скобки и делать решение проще.
- (AՈB)ՈC = AՈ(BՈC)
- (AUB)UC = AU(BUC)
- Раскрытие скобок или дистрибутивность.
- (AUB)ՈC=(AՈC)U(BՈC)
- (AՈB)UC=(AUC)Ո(BUC)
Разностью A и B называется множество, которое включает в себя все элементы, каждое из которых принадлежит множеству A и не принадлежит множеству B. Обозначается AB. Приведём пример, найдём разность множеств A = {1,2,3,4,5} и множества B = {2,4,6,8}. Первый вариант находим разность множества A. Запись будет выглядеть так: AB={1,3,5}, в которую не входят элементы, принадлежащие только B числа 6 и 8. Разность множества B при этом выглядит так: BA={6,8}, сюда соответственно не входят числа, принадлежащие только A.
Для закрепления материала пройденных уроков, рассмотрим ещё несколько примеров. Дана задача: A = {0,5,8,10}, B = {3,6,8,9} и X = {0,1,3} Y = {2,4,6}. Найдите пересечение, объединение для A, B и разность множеств X, Y. Решение:
Сначала найдём объединение исходных множеств A U B = {0,3,5,6,8,9,10}.
Затем пересечение A Ո B = {8}
Разность XY = {0,1,3} YX = {2,4,6}
Для того, чтобы выполнить операции над множествами пересечения, объединения, разность в количестве больше двух, следует рассматривать элементы, входящие в первое их них. Затем определить, относится ли этот элемент к каждому из проверяемых множеств. Если данное обстоятельство не соблюдено, то элемент не относится к пересечению. При проверке, лучше выбирать множество с наименьшим количеством элементов в составе.
Кроме перечисленных действий пересечения и объедения существует дополнение множеств и многие другие операции.
Нет времени решать самому?
Наши эксперты помогут!
Отображение множеств с помощью координатной прямой
Для того, чтобы исследовать и обозначать множества, удобно применять выделение числовых промежутков на координатной прямой. Каждая выбранная точка разделяет находящиеся на ней числа на два открытых луча. Приведём пример, точка с координатами 42,7 сформирует промежутки, которые можно записать как (-∞,42,7) и (42,7, +∞). Наше выражение заключено в круглые скобки, это значит, что сама точка 42,7 ни одному из этих промежутков не принадлежит. Числовая прямая, которая записывается как R = (-∞,+∞), при таком варианте из нашего примера, представляет объединение:
(-∞,42,7) U {42,7} U (42,7+∞).
При добавлении нашей рассматриваемой точки 42,7 к одному из представленных (-∞,42,7) или (42,7, +∞) числовых лучей, в таком случае промежуток перестанет быть открытым. При записи выражения нужно будет использовать квадратные скобки, которые обозначают, что точка входит в промежуток. Запись будет выглядеть так: (-∞,42,7] и [42,7+∞). Тем самым множество действительных чисел на координатной прямой будет выглядеть так:
(-∞,42,7] U (42,7+∞) или (-∞,42,7) U [42,7+∞).
На числовой прямой можно выполнять большое количество действий. Такую прямую можно разделить на отрезки не точкой, как в предыдущем примере, а лучом или отрезком. Все выявленные закономерности так же будут соблюдены. Кроме того, они выполняются при разделении самих числовых промежутков. Рассмотрим пример, точка с координатой 18 на промежутке (8,34] разделит его на следующие промежутки (8,18) U {18} U (18,34]. Дополнив точкой, один из промежутков, получатся следующее записи: (8,18] U (18,34], (8,18) U [18,34]. Примем за разделяющую точку цифру 34, которая включается в состав рассматриваемого промежутка и ограничивает его справа. В результате получим объединение множеств {34} и интервала (8,34) либо (8,34] = (8,34) U {34}
Аналогичные закономерности объективны и в ситуации, когда координатная прямая разделяется на промежутки несколькими точками. К примеру, точки -5, 0 и 6 разделят её на промежутки (-∞,-5), (-5,0), (0,6), (6,+∞), при этом множество действительных чисел (-∞,-5) U {-5} U (-5,0) U {0} U (0,6) U {6} U (6,+∞).
Благодаря координатной прямой достаточно просто и легко рассматривать пересечения и объединения множеств. Они указываются друг под другом на координатных прямых с идентичными направлениями отсчёта и точками. При записи отображения множеств координатные прямые обозначают слева квадратной скобкой, фигурные скобки используются, чтобы показать пересечение.
С помощью дополнительной координатной прямой, которую располагают ниже исходной, показываются искомые пересечения или объединение. На ней поперечными чертами отмечают граничные точки первичных множеств, а после выяснения характера точек, их заменяют полями или сплошными. На рисунке вхождение промежутка в объединение показывается штриховкой, отсутствие вхождения – полой точкой, а вхождение – сплошной.
Графически пересечение A и B показывается промежутками, над которыми имеется штриховка, дополненная отдельными точками, которые принадлежат обоим множествам. На рисунке объединение проявляется там, где показана штриховка хотя бы у одного из множеств и сплошные точки.
В приведённых примерах объединения и пересечения множеств указаны только целые числа. Отрезкам на координатной прямой так же принадлежат и другие числа, которые целыми не являются, такие как десятичные дроби. При определении пересечения и определения множеств, класс чисел намного шире, чем представлен в упражнениях, они находятся между целыми числами и количество их очень велико, перечислять которые не представляется возможным.
В математике важную
роль играют множества, составленные из
«математических» объектов – чисел,
точек, геометрических фигур и т.д.
Примерами числовых множеств являются:
-
множество
всех действительных чисел R; -
множество
всех рациональных чисел Q; -
множество
всех натуральных чисел N; -
множество
всех целых чисел Z; -
множество
всех иррациональных чисел L.
Рассмотрим
основные понятия, характеризующие
множество точек на прямой.
1. Интервалы.Еслиaиbдва действительных числа иa<b, то множество всех
чиселx, удовлетворяющих
неравенствуa<x<b, называетсяоткрытым интервалом(числовым
промежутком) и обозначается (a,b). Сюда же относятся
интервалы (– ∞; + ∞), (– ∞;a),
(b; + ∞).
Открытый
интервал не имеет ни наименьшего, ни
наибольшего числа: какое бы число x
(a;
b)
мы не взяли, обязательно на этом
интервале найдутся такие x΄
и x˝,
что x΄
> x,
x˝
< x.
Множество всех точек любого интервала
является бесконечным. На числовой
прямой открытые интервалы изображаются
следующим образом:
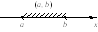

Замкнутый
интервал
(числовой отрезок) [a;
b]
состоит из всех чисел x,
для которых a
≤ x
≤ b,
или [a;
b]
= (a;
b)
{a}
{b}.
На числовой прямой замкнутые интервалы
изображаются следующим образом:
Интервалы
смешанного типа
состоят из всех чисел x,
для которых:
a
≤ x
< b,
или
[a,
b)
= (a,
b)
{a};
a
< x
≤ b,
или
(a,
b]
= (a,
b)
{b};
∞ <
x
≤ a,
или
(– ∞, a]
= (– ∞, a)
{a};
b
≤ x
< + ∞, или
[b,
+ ∞) = (b,
+ ∞)
{b}.
На числовой прямой
смешанные интервалы изображаются
следующим образом:


2.
Окрестность
точки.
Окрестностью
точки х0
называется любой открытый интервал,
содержащий эту точку. Возьмем какое-либо
положительное число ε.
ε-окрестностью
точки х0
называется открытый интервал с центром
в точке х0
и длиной 2ε,
то есть интервал (х0
– ε;
х0
+ ε).
3. Множества
точек, задаваемых алгебраическими
уравнениями и неравенствами. С каждым
уравнением связаны два числовых
множества. Первое из них –область
определения уравнения. Это множество
состоит из всех значенийx,
для которых имеют смысл обе части
уравнения. Второе множество – этомножество корней уравнения, то есть
чисел, при подстановке которых в
уравнение, оно обращается в тождество.
►Пример
6.1. Областью
определения уравнения
=
2 – x
является
множество [- 4; + ∞), так как x
+ 4 ≥ 0, x
≥ 4.
Найдем корни
уравнения. Возведем обе части в квадрат
x
+ 4 = (2 – x)2; x2
– 5x
= 0; х·(х
– 5) = 0;
х1
= 0; х2
= 5.
Оба
числа х1
= 0 и х2
= 5 принадлежат множеству [- 4; + ∞), однако
число х2
= 5 является посторонним корнем уравнения
(это показывает простая проверка:
≠
2 – 5). Таким образом, множество корней
данного уравнения {0}
[- 4; + ∞). На числовой прямой эти множества
изображаются так:
Те же рассуждения
относятся и к алгебраическим неравенствам.
Пример
6.2. Решить
систему неравенств
Первое
неравенство х
– 2 ≤ 0 имеет множество решений х
≤ 2, или х
(– ∞; 2]:
Во втором неравенстве
находим корни:
х2
– 5х
– 6 = 0; х1
= – 1, х2
= 6.
Решением его
будет интервал х(– 1; 6):
Чтобы
получить решение системы неравенств,
нужно найти пересечение множеств (– ∞;
2]
(– 1; 6). Покажем эти множества на числовой
прямой:
Как видно из
рисунка, пересечением является интервал
смешанного типа х(– 1; 2], на котором штриховки накладываются
друг на друга. ◄