Решение некоторых математических задач предусматривает операции над множествами такие как пересечение, объединение, разность. Под множеством подразумевают объединение некоторых предметов в одно целое. Для совершения подобных действий требуется знание некоторых правил, которые позволят найти пересечение, объединение и разность множеств. О таких правилах пойдёт речь далее.
Обозначение множеств. Как записать объединение и пересечение множеств
Определения
Объединение множеств – это ряд таких элементов, при которым каждый из них представляет собой элемент одного из первоначальных множеств.
Пересечение множеств — заключает в себе все элементы, общие для первоначальных множеств.
При записи обозначения пересечения множеств и объединения множества чисел, используют специальный порядок символов. Самый лёгкий способ обозначить множество — это применение фигурных скобок, в середине которых элементы записаны через запятую.
А = {7, 3, 15, 31}
С помощью такой записи можно задать множество, если оно включает небольшое конечное число элементов. В связи с этим чаще применяется многофункциональный способ определения множеств – посредством характеристического свойства, которое свойственно всем элементам множества, которым не владеют объекты вне множества.
A = {x | P(x)} или A = {x : P(x)}
P(x) – характеристическое свойство множества A.
В таком виде объединение записывается следующим образом:
AUB={x|xєAvxєB}
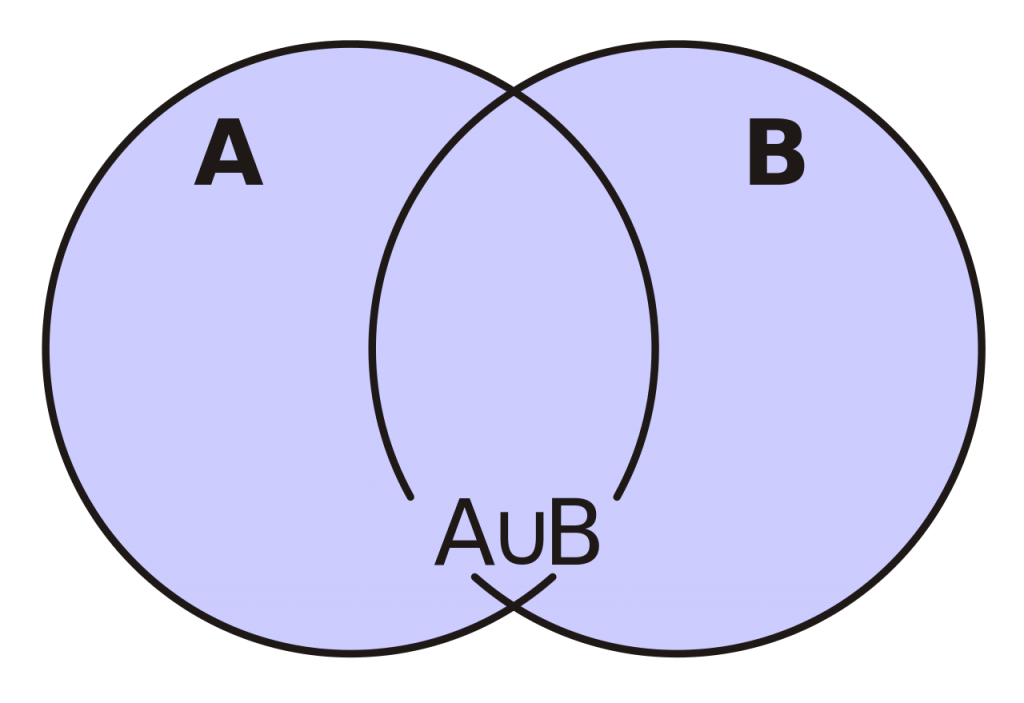
а пересечение множеств записывается как:
AՈB={x|xєAᴧxєB}
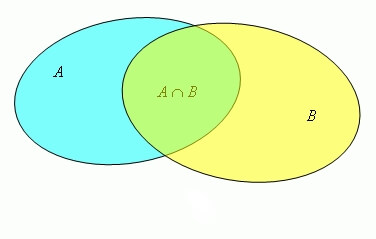
Где символы v / ᴧ, обозначают «или» / «и», символ | обозначает «таких что».
Чтобы обозначить множества, как числовые интервалы, при записи применяют скобки круглой и квадратной формы. К примеру, запись [4,24), выражает цифровой диапазон от 4 до 24, при этом число 4 входит в состав множества, а 24 нет. Числа менее 24 принадлежат этому множеству.
Найти пересечение и объединение множеств. Операции над множествами
Важно
U – обозначает объединение множеств A и B;
Ո – обозначает пересечение множеств A и B.
Чтобы легче запомнить данные знаки пересечения и объединения множеств, можно мысленно представить, что символ объединения U напоминает сосуд с открытым верхом, туда есть возможность что-то положить.
Символ пересечения Ո наоборот, выглядит как перевёрнутая ёмкость, в который невозможно поместить какой-либо предмет. Так же символ обозначающий пересечение Ո можно прочитать как «И».
Тогда выражение AՈB=C, читается так: “Все элементы, входящие в состав множества A и множества B, составляют элементы, которые принадлежат множеству C».
Правила нахождения объединения и пересечения и разности множеств
При формировании объединения числовых множеств, следует последовательно записать полностью части одного множества и их дополнить недостающими элементами из остальных. Операцию объединения в отдельных случаях называют сложением множеств и обозначают знаком «+».
Рассмотрим пример объединения числовых множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10}. К имеющимся числовым составляющим множества A 1,2,3,4,5,6,7,8,9 прибавим недостающую часть из множества B 10. Получившееся в результате объединения множество чисел будет выглядеть так {0,1,2,3,4,5,6,7,8,9,10}. Соответственно запись этого объединения:
AUB={0,1,2,3,4,5,6,7,8,9,10}
Чтобы составить пересечение числовых множеств, следует последовательно выбирать части одного множества и удостовериться, входят ли они в другие исследуемые множества, входящие в их число и составляют пересечение.
Для того, чтобы найти пересечение этих же множеств, друг за другом, последовательно проанализируем числа множества A на их наличие в множестве чисел B. Начнём проверку с самого первого числа в множестве A это число 0. В множестве B данное число отсутствует и не войдёт в совокупность пересечения. Смотрим далее, число 1 из множества A так же имеется в составе множества B. Затем следует число 2, которое принадлежит множеству B и, следовательно, пересечению. Идущее за ним 3 не принадлежит A и B не входит в перечисление. Число 4 входит в A и B, значит войдёт и в объединение. Далее продолжаем проверять числа по аналогии. Итак, пересечение множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10} состоит из чисел 2,4,6,8. При записи выглядит так:
AՈB={2,4,6,8}
Выполнение записи пересечения и объединения нескольких множеств
Если требуется выполнить операции с более чем двумя множествами, например: A, B, C, принцип действия подобный предыдущим примерам. В первую очередь находим пересечения A и B. Только затем пересечение полученного множества с C.
Следовательно, процесс нахождения пересечения более двух множеств осуществляется в несколько этапов.
Например, дано три множества A = {1,2,3,7,9}, B = {1,3,5,7,9} и C = {3,4,5,8,9}. Сначала находим пересечение AՈB = {3,9}, затем сравниваем полученное множество с C, это будут те же 3 и 9. Получаем, что пересечение A, B, C выглядит следующим образом:
AՈBՈC={3,9}
При определении объединений двух и более множеств, к числам первого множества последовательно добавляют отсутствующие элементы из второго, третьего и последующих множеств. К примеру, даны следующее множества A = {1,4}, B = {4,3,} и C = {1,3,6,7}. К числовым элементам 1 и 4 из множества A, прибавляем число 4 из множества B. Теперь, к получившемуся множеству 1,3,4 прибавляем цифры 6 и 7 из множества C. В конечном результате получаем объединение:
AUBUC = {1,3,4,6,7}
Для нахождения пересечения совсем не нужно писать много букв. Когда элементов не много, то множество возможно задать элементарным перечислением. Например, первое множество включает в себя числа 1,3,5, второе состоит из элементов 2,3,5. В данном случае, пересечение будет состоять из элементов 3 и 5. Для записи можно использовать прямое перечисление: {1,3,5} Ո {2,3,5} = {3,5}
Основные свойства объединения и перечисления множеств
- Коммутативность или перестановка. Распространяется на все компоненты при любом их количестве.
- AUB = BUA
- AՈB = BՈA
- Ассоциативность или расстановка скобок. Позволяет опускать скобки и делать решение проще.
- (AՈB)ՈC = AՈ(BՈC)
- (AUB)UC = AU(BUC)
- Раскрытие скобок или дистрибутивность.
- (AUB)ՈC=(AՈC)U(BՈC)
- (AՈB)UC=(AUC)Ո(BUC)
Разностью A и B называется множество, которое включает в себя все элементы, каждое из которых принадлежит множеству A и не принадлежит множеству B. Обозначается AB. Приведём пример, найдём разность множеств A = {1,2,3,4,5} и множества B = {2,4,6,8}. Первый вариант находим разность множества A. Запись будет выглядеть так: AB={1,3,5}, в которую не входят элементы, принадлежащие только B числа 6 и 8. Разность множества B при этом выглядит так: BA={6,8}, сюда соответственно не входят числа, принадлежащие только A.
Для закрепления материала пройденных уроков, рассмотрим ещё несколько примеров. Дана задача: A = {0,5,8,10}, B = {3,6,8,9} и X = {0,1,3} Y = {2,4,6}. Найдите пересечение, объединение для A, B и разность множеств X, Y. Решение:
Сначала найдём объединение исходных множеств A U B = {0,3,5,6,8,9,10}.
Затем пересечение A Ո B = {8}
Разность XY = {0,1,3} YX = {2,4,6}
Для того, чтобы выполнить операции над множествами пересечения, объединения, разность в количестве больше двух, следует рассматривать элементы, входящие в первое их них. Затем определить, относится ли этот элемент к каждому из проверяемых множеств. Если данное обстоятельство не соблюдено, то элемент не относится к пересечению. При проверке, лучше выбирать множество с наименьшим количеством элементов в составе.
Кроме перечисленных действий пересечения и объедения существует дополнение множеств и многие другие операции.
Нет времени решать самому?
Наши эксперты помогут!
Отображение множеств с помощью координатной прямой
Для того, чтобы исследовать и обозначать множества, удобно применять выделение числовых промежутков на координатной прямой. Каждая выбранная точка разделяет находящиеся на ней числа на два открытых луча. Приведём пример, точка с координатами 42,7 сформирует промежутки, которые можно записать как (-∞,42,7) и (42,7, +∞). Наше выражение заключено в круглые скобки, это значит, что сама точка 42,7 ни одному из этих промежутков не принадлежит. Числовая прямая, которая записывается как R = (-∞,+∞), при таком варианте из нашего примера, представляет объединение:
(-∞,42,7) U {42,7} U (42,7+∞).
При добавлении нашей рассматриваемой точки 42,7 к одному из представленных (-∞,42,7) или (42,7, +∞) числовых лучей, в таком случае промежуток перестанет быть открытым. При записи выражения нужно будет использовать квадратные скобки, которые обозначают, что точка входит в промежуток. Запись будет выглядеть так: (-∞,42,7] и [42,7+∞). Тем самым множество действительных чисел на координатной прямой будет выглядеть так:
(-∞,42,7] U (42,7+∞) или (-∞,42,7) U [42,7+∞).
На числовой прямой можно выполнять большое количество действий. Такую прямую можно разделить на отрезки не точкой, как в предыдущем примере, а лучом или отрезком. Все выявленные закономерности так же будут соблюдены. Кроме того, они выполняются при разделении самих числовых промежутков. Рассмотрим пример, точка с координатой 18 на промежутке (8,34] разделит его на следующие промежутки (8,18) U {18} U (18,34]. Дополнив точкой, один из промежутков, получатся следующее записи: (8,18] U (18,34], (8,18) U [18,34]. Примем за разделяющую точку цифру 34, которая включается в состав рассматриваемого промежутка и ограничивает его справа. В результате получим объединение множеств {34} и интервала (8,34) либо (8,34] = (8,34) U {34}
Аналогичные закономерности объективны и в ситуации, когда координатная прямая разделяется на промежутки несколькими точками. К примеру, точки -5, 0 и 6 разделят её на промежутки (-∞,-5), (-5,0), (0,6), (6,+∞), при этом множество действительных чисел (-∞,-5) U {-5} U (-5,0) U {0} U (0,6) U {6} U (6,+∞).
Благодаря координатной прямой достаточно просто и легко рассматривать пересечения и объединения множеств. Они указываются друг под другом на координатных прямых с идентичными направлениями отсчёта и точками. При записи отображения множеств координатные прямые обозначают слева квадратной скобкой, фигурные скобки используются, чтобы показать пересечение.
С помощью дополнительной координатной прямой, которую располагают ниже исходной, показываются искомые пересечения или объединение. На ней поперечными чертами отмечают граничные точки первичных множеств, а после выяснения характера точек, их заменяют полями или сплошными. На рисунке вхождение промежутка в объединение показывается штриховкой, отсутствие вхождения – полой точкой, а вхождение – сплошной.
Графически пересечение A и B показывается промежутками, над которыми имеется штриховка, дополненная отдельными точками, которые принадлежат обоим множествам. На рисунке объединение проявляется там, где показана штриховка хотя бы у одного из множеств и сплошные точки.
В приведённых примерах объединения и пересечения множеств указаны только целые числа. Отрезкам на координатной прямой так же принадлежат и другие числа, которые целыми не являются, такие как десятичные дроби. При определении пересечения и определения множеств, класс чисел намного шире, чем представлен в упражнениях, они находятся между целыми числами и количество их очень велико, перечислять которые не представляется возможным.
Объединение множеств A и B являет собой такое же, как и исходные, множество, в составе которого наличествуют элементы, принадлежащие одному или прочим из объединяемых множеств. Удостоверяет объединение двух множеств наличие в обозначении между ними специального знака, напоминающего латинскую букву «U».
Понять, как происходит объединение множеств легко на простом примере:
Если A ={1, 3, 5, 7} и B ={2,4,6,8,9}, то A U B = {1,2,3,4,5,6,7,8,9}.
Или: если A ={1, 5, 8} и B ={2,5,7,8,9}, то A U B = {1,2,5,7,8,9}
В отношении объединения множеств действует коммутативный и ассоциативный законы. Задействуются вычисления объединения множеств наравне с разностью и пересечением множеств при решении различных задач алгебры логики и профильной алгебры множеств, при проектировании сложной микропроцессорной и иной электронной техники.
Операции над множествами.
-
Логические.
a={1,
2, 3, 4, 5, 6, 7}
B={4,
5, 6, 7, 8, 9, 10}
BUC={2,
4, 5, 6, 7, 8, 9, 10}
C={2,
4, 6, 8, 10}
V={1,
2, 2, 4, 5, 6, 7, 8, 9, 10}
-
auc={1,
2, 3, 4, 5, 6, 7, 8, 9, 10} -
a∩b={4,
5, 6, 7} -
a∩(buc)={2,
4, 5, 6, 7} -
(a∩b)uc={2,
4, 5, 6, 7, 8, 10} -
⌐(a∩b)={1,
2, 3, 8, 9, 10} -
⌐a∩⌐b={8,
9, 10}∩{1, 2, 3, }=Ø -
AΔB AB={1,
2, 3}
BA={8, 9, 10}
AΔB={1, 2, 3, 8, 9, 10}
-
AB={1,
2, 3}
AΔB=⌐(A∩B)
-
Умножение.
A={1, 2, 3}
B={a, b}
-
AxB={(1,
a), (1, b), (2, a), (2, b), (3, a), (3, b)} -
BxB={(aa),
(bb), (ab), (ba)} -
Ax
Ø= Ø
-
Определить множество.
P(A), если A
Ø { Ø }
P(A), A={ Ø, { Ø }} 4 {{ Ø } {{ Ø }} Ø { Ø {
Ø }}}
-
Наследником
множества А называется АU{A}.
Определить наследников множеств.
-
Ø ØU{
Ø } -
{
Ø } {{ Ø }, Ø
} -
{
Ø ,{ Ø }} {{ Ø
}, Ø, { Ø, {
Ø }}}
-
Логические
операции над множествами.
a={1,
2, 3, 4, 5, 6, 7}
B={4,
5, 6, 7, 8, 9, 10}
C={2,
4, 6, 8, 10}
-
AC={1,
3, 5, 7} -
AΔC={1,
2, 3, 8, 9, 10} -
(AB)U(BA)={1,
3, 5, 7, 8, 9, 10} -
(A∩C)⌐B={4,
5, 6, 7, 8, 9, 10} -
A∩(B∩⌐C)={5,
7} -
(A
Ø)U(AA)={ Ø , 1, 3,
4, 5, 6, 7, 8} -
CA={8,
10}
-
Определить
истинность.
AU Ø=A 1
AΔ Ø=A 1
Если A≤B,
то AUB=A 0
Если AUB=A,
то B≤A 1
A Ø=A 1
-
Используя
диаграммы венна закрасить те части,
которые изображают множества.
AB
B
A
(a∩b)
B
A
(А
u В)
(А
∩ В)
B
A
au(b∩c)
C
B
A
(A∩B∩C)
C
B
A
B(AUC)
C
B
A
(B∩C)A
C
B
A
-
Используя
диаграммы венна доказать.
⌐(A∩B)=⌐AU⌐B
B
A
B
A
-
⌐A
⌐B
AUB
au(b∩c)=
(aub)∩(auc)
-
(aub)∩(auc)
(aub)
(auc)
-
Используя
диаграммы венна нарисовать.
AΔB
B
A
⌐(AUB)
B
A
A(A∩B)
B
A
(A∩B)ΔC
C
B
A
(AUBUC)(A∩B∩C)
C
B
A
(A∩B)U(B∩C)U(A∩C)
C
B
A

(AB)U(BC)
-
Доказать.
(AUB)=A∩B
B
A
(aUb)
A
B
A∩(BUC)=(A∩B)U(A∩C)
A∩(BUC)
(A∩B)
(A∩C)
-
Задание не помню.

-
-
Qn=
-
Qn+1=
Qn=
2Qn=n(n-1)
2Qn=
-
Используя
таблицу истинности доказать.
⌐(pΛq)≡⌐pv⌐q
-
p
q
pΛq
⌐(pΛq)
⌐p
⌐q
⌐pv⌐q
0
0
0
1
1
1
1
0
1
0
1
1
0
1
1
0
0
1
0
1
1
1
1
1
0
0
0
0
pv(qvr)≡(pvq)vr
-
p
q
r
qvr
pv(qvr)
pvq
(pvq)vr
0
0
0
0
0
0
0
0
0
1
1
1
0
1
0
1
0
1
1
1
1
0
1
1
1
1
1
1
1
0
0
0
1
1
1
1
0
1
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
pv(qΛr)≡(pvq)Λ(pvr)
-
p
q
r
qΛr
pv(qΛr)
pvq
pvr
(pvq)Λ(pvr)
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
0
0
0
1
1
1
1
1
0
1
0
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1
p→q≡⌐pvq
-
p
q
p→q
⌐p
⌐pvq
0
0
1
1
1
0
1
1
1
1
1
0
0
0
0
1
1
1
0
1
-
Не
используя таблицу истинности доказать.
⌐(p→q)≡pΛ⌐q
⌐(⌐pvq)≡pΛ⌐q
⌐(pvq)≡⌐pΛ⌐q
⌐(⌐p)≡p
-
Доказать, что контропозиция и инплекация
эквивалентны инплекации. Без таблицы.
⌐p→⌐q≡p→q
qv⌐p ≡⌐pvq
-
Доказать
эквивалентность.
p≡⌐(pΛs)→(⌐sΛp)
(pΛs)v(⌐sΛp)
p≡pΛ(sv⌐s)
p≡p
-
С помощью
таблицы истинности доказать.
⌐(pvq)≡⌐pΛ⌐q
-
p
q
pvq
⌐(pvq)
⌐p
⌐q
⌐pΛ⌐q
0
0
0
1
1
1
1
0
1
1
0
1
0
0
1
0
1
0
0
1
0
1
1
1
0
0
0
0
pΛ (qΛr)≡(pΛq) Λr
-
p
q
r
qΛr
pΛ (qΛr)
pΛq
(pΛq) Λr
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
1
1
1
0
0
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
1
1
0
0
0
1
0
1
1
1
1
1
1
1
pΛ (qvr)≡(pΛq)
v (pΛr)
-
p
q
r
qvr
pΛ(qvr)
pΛq
pΛr
(pΛq)v(pΛr)
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
Графы.
-
Найти
длину и характер пути.
a b c

d e f
-
aebfcd
— путь простой, длина 5 -
aecdaec
— путь не простой, длина 6 -
aebcfbd
— не путь -
aecfbdafc
— путь простой, длина 8
a d

b c e
-
abcabcd
— путь не простой, цикл – abc,
длина 6 -
bcdeca
— путь не простой, длина 5 -
debace
— не путь -
decab
— путь простой, длина 4
-
Найти
длину, характер пути и цикл.
a b c

d e f
-
dabcfbed
—не путь -
bfcedbfcb
— цикл не простой, длина 8 -
abcfebfca
— не путь -
aecfbda
— цикл не простой, длина 6
-
Нарисовать
граф.
-
K6
a b c

d e f
-
K1,3
a
b c d
-
K3,4
a b c

d e f g
-
Найти
наименьший оющий делитель.
НОД(126, 69)
126=69*1+57
69=57*1+12
57=12*4+9
12=9*1+3
9=3*3+0
-
Найти
матрицы инцидентности для графов.
-
e1
e2
e3
e4
e5
e6
V1
1
0
0
0
1
1
V2
1
1
0
0
0
0
V3
0
1
1
0
0
0
V4
0
0
0
1
1
0
V5
0
0
1
1
0
1
-
e1
e2
e3
e4
e5
e6
V1
1
0
0
1
0
0
V2
1
1
1
0
0
0
V3
0
1
0
0
1
1
V4
0
0
1
1
1
0
V5
0
0
0
0
0
1
-
-
e1
e2
e3
e4
e5
e6
e7
e8
e9
e10
V1
1
0
0
0
1
1
0
0
1
0
V2
1
1
0
0
0
0
1
0
0
1
V3
0
1
1
0
0
1
0
1
0
0
V4
0
0
1
1
0
0
1
0
1
0
V5
0
0
0
1
1
0
0
1
0
1
-
Для этих
же грфов найти матрицы смежности.
-
V1
V2
V3
V4
V6
V1
0
1
0
1
1
V2
1
0
1
0
0
V3
0
1
0
0
1
V4
1
0
0
0
1
V5
1
0
1
1
0
-
V1
V2
V3
V4
V6
V1
0
1
0
1
0
V2
1
0
1
1
0
V3
0
1
0
1
1
V4
1
1
1
0
0
V5
0
0
1
0
0
-
V1
V2
V3
V4
V6
V1
0
1
1
1
1
V2
1
0
1
1
1
V3
1
1
0
1
1
V4
1
1
1
0
1
V5
1
1
1
1
0
-
Построить граф для матрицы инцидентности.
-
1
0
1
0
0
1
0
0
0
1
0
1
0
0
1
0
0
1
1
0
1
0
0
1
1
0
0
1
1
0
0
0
0
0
0
0
0
1
1
1

-
По
матрице смежности построить граф.
-
0
0
1
0
1
0
0
0
1
0
1
1
1
1
0
1
0
0
0
0
1
0
1
1
1
1
0
1
0
0
0
1
0
1
0
0
V1

-
Построить граф определяющий расписание
группы нашей в качестве вершин и дни
недели. Две вершины соединены, если в
этот день есть этот предмет.

1 – физика
2 – дискретная математика
3 – физкультура
4 – основы экономической теории
5 – начертательная геометрия
6 – математический анализ
7 – программирование
8 – технология программирования
9 – иностранный язык
e
-
Для
указанного графа найти матрицу смежности
и используя ее найти пути длинной 2 и
3.
b
a
d
c
-
a
b
c
d
e
a
0
0
1
1
0
b
0
0
1
1
0
c
1
1
0
1
1
d
1
1
1
0
1
e
0
0
1
1
0
ace, ade, acb,
adb, acd, adc,
bca, bcd, bce,
bda, bdc, bde,
cad, cbd, cda,
cdb, cde, ced,
…
aced, acbd, acdb,
adbc, adcb, adec,
acde, adce, bcad,
bced, bcde, bcda,
bdec, bdac, bdca,
bdce, …
-
Доказать
утверждение:
Пусть G ориентированный
граф с вершинами v1,
v2, v3,
…, vn
и матрицей смежности A.
Из вершины v1 в
вершину vj
тогда существует m путей
длинны 1≤k≤n,
когда Akij=m.
Akij
— элемент матрицы Ak
на пересечении i — строки
и j — столбца.
Доказательство:
Akij=m
-
k=1 Akij=1
-
k=n Akij=mn
-
k=n+1
Aijn+1=mn+1
Aijn+1=(An*A)ij=Ai1n*A1j+Ai2n*A2j+…=
ikn*Akj=mn+1
-
сколько
натуральных чисел меньше 700 делится на
3; на 5; и на 3, и на 5.
699/5=139 на 5
699/3=233 на 3
699/3/5=46 и на 3, и на 5
-
сколько
существует способов избрания президента,
вице – президента, секретаря и казночея
студенческого клуба среди 8 человек
4курса, 10 человек 3курса, 15 человек 2курса
и 20человек 1курса, если:
-
нет
ограничений; -
президентом
может быть только человек 4курса; -
никто
с 4курса не может быть вице – президентом; -
учащийся
на 1курсе могут быть только секретарем.
-
53!/49!
-
8*52*51*50
-
52*51*50*45
-
33*32*31*50
-
Сколько
существует 4 – значных чисел, если по
крайней мере 2 цифры в числе совпадают.
C310=10/(7!*3!)
-
Сколько
существует различных функций из 6
элементного множества в 3 элементном
множестве.
6!/3!=20*6=120
-
Сколько
существует бинарных строк длинны 7.
-
Нет
ограничений; -
Первый
и последний бит совпадает; -
Содержащие
две и более единицы.
-
27
-
26
-
25-1
-
Сколькими
способами можно числа меньше 10 так,
чтобы 4 было сразу после 5 или 5 сразу
после 4.
16*7!
-
Сколько
целых чисел между 1 и 401 делятся на 5 или
7.
400/5=80 на 5
400/7=57 на 7
400/7/5=11 и на 5, и на 7
80+57-11=126
Ответ: 126.
Делятся на 6 или на 10.
400/6=66 на 6
400/10=40 на 10
66+40-13=93 ответ.
-
Сколько
существует натуральных чисел содержащих
не более 5 цифр.
-
Первая
цифра 3; -
Последняя
цифра 5; -
Или
первая 3, или последняя 5; -
Ни первая
3, ни последняя 5.
-
11111
-
10000
-
20000
-
79999
-
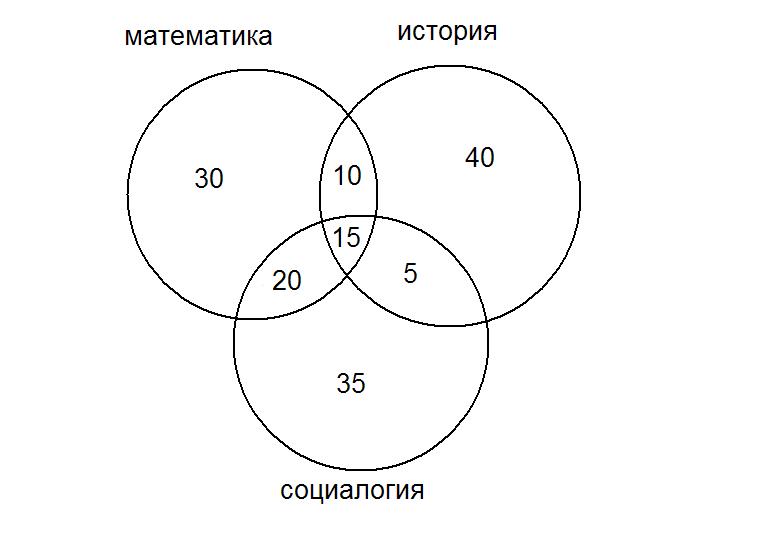
В группе
из 200 студентов 75 студентов изучают
математику, 70 историю, 75 социологию, 35
математику и социологию, 25 математику
и историю, 20 историю и социологию, 15 все
трипредмета.
-
Сколько
человек изучаетхотя бы один предмет; -
Только
одиниз трех; -
Историю
или математику ,но не социологию; -
Не
изучают 2 из 3; -
Не изучают
математику или историю.
-
155
-
105
-
70
-
165
-
80
-
Сколько
целых чисел между 1 и 1001
а) делятся на 10, но не делятся на 40;
б) делятся на 10, но не делятся на 14.
г) Между 1 и 2003 делятся на 4, 5 или 6.
а) 1000/10-1000/40=75
б) 1000/10-1000/70=86
г) 500+400+333-100-166-66+33=934
-
А) Сколько
3-значных чисел можно образовать
используя цифры 2, 3, 4, 5, 6, 7, 8, 9;
Б) Сколько таких чисел меньше 450;
В) Сколько среди них четных чисел ;
Г) Сколько из них делятся на 4.
А) 73=343
Б) 1*3*7+2*7*7=119
В) 7*7*4=196
Г) 7*14=98
-
Сколько
существует восьми битных строк содержащих
3 нуля и 5 единиц.
8!/(5!*3!)=56
-
Сколько
существует способов вытащить 13 картиз
станлартной колоды, содержащей 52 карты,
если
А) нет ограничений;
Б) 6 карт одной масти;
В) 7 карт одной масти;
Г) 8 карт одной масти;
Д) 9 карт одной масти.
А) 52!/(13!*39!)
Б) 39!*4/((39-7)!*7!)
В) 13!/(7!*6!)
Г) 13!/(8!*5!)
Д) 13!/(9!*4!)
-
Сколько
различных колекций из 10 монет можно
собрать из монет стоимостья 1, 5, 10, 25, 50
(n+k+1)!/(n!(k-1)!)=14!/(10!4!)=1001
-
Если в
урне имеется 20 красных, 20 зеленых и 20
синих шаров, то сколькими различными
способами можно выбрать 10 шаров.
12!/(10!2)=66
-
Человек
покупает 12 различных игрушек для 4
детей.
А) сколькими способами он может разделить
игрушки;
Б) сколькими способами можно разделить
игрушки поровну.
А) (12+3)!/(12!*3!)=455
Б) (3+11)!/(3!*11!)=364
-
Решитьнайти
рекуррентные функции.
А) an=n2an-1—
an-2
Б) an=a2n-1-an-2
В) an=an-1+
an-2
Г) an=an-1+3an-2*an-3
Д) an=an-1+3an-2-nan-3
а, в, д
-
Найти
общее решение для рекурсивных отношений.
А) an-3an-1=0
Б) an+3an-1=0
В) an=-an-1-6an-2
Г) an=an-1-3an-2
А)
rn-3rn-1=0
r-3=0
r=3
an=c3n
Б) r+3=0
r=-3
an=c(-3)n
В) rn=
-rn-1+6rn-2
r=-3;3
an=c(-3)n-1+drn-2
Г) rn=
-rn-1+3rn-2
r2
-r-3 =0
r=(1+-
)/2
an=c(1-
)/2+d(1+
)/2
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Объединение множеств
Простые и составные числа
Известно, что объединением множеств А и В будет считаться множество С, при условии, что оно содержит все элементы хотя бы одного из множеств А или В, либо одновременно А и В. Символами «U» и «+» обозначается объединение множеств, в письменном виде его можно выразить таким образом:
C = A U B
или C = A + B
Например, для множеств А = {-4, -2, 0, 2, 4} и B = {0, 2, 4, 6, 8, 10} объединение множеств будет записываться следующим образом A U B = {-4, -2, 0, 2, 4, 6, 8, 10}. Аналогично можно определить объединение любого числа заданных множеств.
Свойства операции объединения множеств:
А ∪ В = В ∪ А
(А ∪ В) ∪ C = А ∪ (B ∪ C)
А ∪ A = A
(А ∪ В) ∩ C = (А ∩ C) ∪ (B ∩ C)
А ∩ В = В ∩ А
(А ∩ В) ∩ C = А ∩ (B ∩ C)
А ∩ A = A
A ∩ (B ∩ C) = (А ∩ B) ∪ (A ∩ C)
Объединением множества рациональных и множества иррациональных чисел будет множество действительных чисел.
Определить объединение множеств вам поможет онлайн калькулятор.
Вычисление объединения двух множеств A и B
Онлайн калькулятор для вычисления объединения двух множеств или соединение двух множеств A и B (AUB). Объединение двух множеств состоит из всех элементов двух множеств.
Примеры:
- {1, 2} ∪ {1, 2} = {1, 2}.
- {1, 2} ∪ {2, 3} = {1, 2, 3}.
- {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}
Некоторые основные свойства объединений множеств:
- A ∪ B = B ∪ A.
- A ∪ (B ∪ C) = (A ∪ B) ∪ C.
- A ⊆ (A ∪ B).
- A ∪ A = A.
- A ∪ ∅ = A.
- A ⊆ B если и только если A ∪ B = B.
людей нашли эту статью полезной. А Вы?