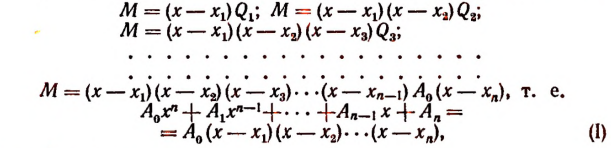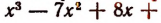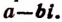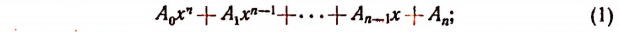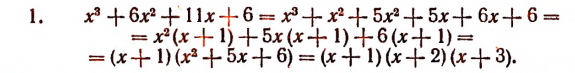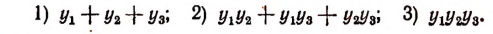Теорема Безу и следствия из неё
19 июля 2022
Теорема Безу позволяет решать уравнения высших степеней, которые на первый взгляд не решаются, и раскладывать на множители многочлены, которые не раскладываются.:)
Формулировка теоремы довольно проста:
Терема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x- color{red}{a}$ равен значению этого многочлена в точке $x= color{red}{a}$:
[r=Pleft( color{red}{a} right)]
На практике нас интересует не сама теорема Безу, а некоторые следствия из неё — именно они помогают решать уравнения и раскладывать многочлены на множители. В этом уроке мы рассмотрим все такие следствия и станем настоящими мастерами в работе с многочленами.
Содержание
- Деление с остатком
- Разложение на множители
- Целые корни многочленов
- Рациональные корни многочленов
- Доказательства
В разных учебниках теорему Безу проходят то в 9-м классе, то в 10-м. Этот урок построен так, что вы поймёте его вне зависимости от школы, класса и учебника.
1. Деление с остатком
Итак, есть многочлен $Pleft( x right)$ и двучлен $x- color{red}{a}$. Разделим $Pleft( x right)$ на $x- color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x- color{red}{a} right)+r]
Теперь найдём значение многочлена $Pleft( x right)$ в точке $x= color{red}{a}$:
[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}- color{red}{a} right)+r=r]
Собственно, мы только что доказали теорему Безу. А заодно подготовили основу для первого важного следствия.
Следствие 1. Деление на произвольный двучлен
Теорема Безу прекрасно работает не только для двучлена $x-color{red}{a}$, но и для любого линейного выражения вида $color{blue}{k}x+color{red}{b}$.
Следствие 1. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $color{blue}{k}x+color{red}{b}$ равен значению этого многочлена в точке $x=-color{red}{b}/ color{blue}{k};$:
[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]
На практике для большей надёжности рекомендуется приравнять двучлен $color{blue}{k}x+color{red}{b}$ к нулю:
[begin{align} color{blue}{k}x+color{red}{b} &=0 \ x &=-frac{color{red}{b}}{color{blue}{k}} \ end{align}]
Затем подставить найденное значение $x=-{color{red}{b}}/{color{blue}{k}};$ в многочлен $Pleft( x right)$ и таким образом найти $Pleft( -{color{red}{b}}/{color{blue}{k}}; right)$:
[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]
Пример 1. Стандартный многочлен
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)=4{{x}^{3}}-3{{x}^{2}}+5x-6]
на двучлен $Tleft( x right)=x-2$.
Решение. Это стандартный двучлен вида $x-color{red}{a}$, поэтому решаем по стандартной теореме Безу, согласно которой остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{2}$ равен $Pleft( color{red}{2} right)$:
[begin{align}r &=Pleft( color{red}{2} right)= \ &=4cdot {color{red}{2}^{3}}-3cdot {color{red}{2}^{2}}+5cdotcolor{red}{2}-6 \ &=32-12+10-6=24 end{align}]
Ответ: 24.
Пример 2. Более сложный многочлен
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)={{left( {{x}^{3}}-2{{x}^{2}}+5 right)}^{3}}{{left( 2x+1 right)}^{5}}]
на двучлен $Tleft( x right)=x+1$.
Решение. Многочлен $Pleft( x right)$ представлен в виде произведения двух других многочленов, которые ещё и возведены в степени. Если раскрыть скобки и привести подобные слагаемые, получится обычный многочлен вида
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
По свойствам степеней найдём степень такого многочлена:
[deg Pleft( x right)=3cdot 3+1cdot 5=14]
Раскрывать скобки и приводить подобные в многочлене 14-й степени долго и трудно, а главное — в этом нет никакой необходимости. Ведь по теореме Безу остаток от деления $Pleft( x right)$ на двучлен $x-color{red}{a}$ всегда равен $Pleft( color{red}{a} right)$ — и не важно, как записан исходный многочлен $Pleft( x right)$.
Для надёжности, чтобы найти $color{red}{a}$, приравняем к нулю двучлен $Tleft( x right)=x+1$:
[begin{align}x+1 &=0 \ x &=color{red}{-1} \ end{align}]
Теперь подставим $x=color{red}{-1}$ в многочлен $Pleft( x right)$ и найдём остаток:
[begin{align}r &=Pleft( color{red}{-1} right)= \ &={{left( {{left( color{red}{-1} right)}^{3}}-2cdot {{left( color{red}{-1} right)}^{2}}+5 right)}^{3}}cdot {{left( 2cdot left( color{red}{-1} right)+1 right)}^{5}}= \ &={{left( -1-2+5 right)}^{3}}cdot {{left( -2+1 right)}^{5}}=-8 end{align}]
Ответ: −8.
Пример 3. Рациональные коэффициенты
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)=3{{x}^{20}}+{{x}^{19}}-7x+1]
на двучлен $Tleft( x right)=3x+1$.
Решение. Воспользуемся Следствием 1 из теоремы Безу. Для надёжности приравняем к нулю двучлен $Tleft( x right)$ и найдём $color{red}{a}$:
[begin{align}3x+1 &=0 \ x &=color{red}{-{1}/{3};} end{align}]
Подставим найденное $x=color{red}{-{1}/{3};}$ в многочлен $Pleft( x right)$ и найдём остаток:
[begin{align} Pleft( color{red}{-frac{1}{3}} right) &=3cdot {{left( color{red}{-frac{1}{3}} right)}^{20}}+{{left( color{red}{-frac{1}{3}} right)}^{19}}-7cdot left( color{red}{-frac{1}{3}} right)+1= \ &=frac{1}{{{3}^{19}}}-frac{1}{{{3}^{19}}}+frac{7}{3}+1=frac{10}{3} end{align}]
Ответ: ${10}/{3};$.
Пример 4. Иррациональные коэффициенты
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)={{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}+64]
на двучлен $Tleft( x right)=left( 1-sqrt{3} right)x+2$.
Решение. Вновь воспользуемся Следствием 1 из теоремы Безу. Приравняем двучлен $Tleft( x right)$ к нулю и найдём $color{red}{a}$:
[left( 1-sqrt{3} right)x+2=0]
Это линейное уравнение с иррациональными коэффициентами. Такое уравнение решается стандартно (см. урок «Линейные уравнения»):
[x=-frac{2}{1-sqrt{3}}=frac{2}{sqrt{3}-1}]
Избавимся от иррациональности в знаменателе, домножив числитель и знаменатель на сопряжённое:
[x=frac{2color{blue}{left( sqrt{3}+1 right)}}{left( sqrt{3}-1 right) color{blue}{left( sqrt{3}+1 right)}}=frac{2left( sqrt{3}+1 right)}{2}= color{red}{sqrt{3}+1}]
Степень исходного многочлена: $deg Pleft( x right)=6$. Если подставить в такой многочлен иррациональное число, то это число придётся возводить в шестую степень. Это слишком долго и трудно, поэтому перепишем многочлен $Pleft( x right)$ так:
[begin{align} Pleft( x right) &=left( {{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}-64 right)+128= \ &={{left( {{x}^{2}}-4 right)}^{3}}+128 end{align}]
Мы выделили точный куб разности — классическую формулу сокращённого умножения. Как это работает — см. уроки «Формулы сокращённого умножения» и «Куб суммы и разности».
В такую формулу намного проще подставить $x=color{red}{sqrt{3}+1}$:
[begin{align}Pleft( color{red}{sqrt{3}+1} right) &={{left( {{left( color{red}{sqrt{3}+1} right)}^{2}}-4 right)}^{3}}+128= \ &={{left( {{left( sqrt{3} right)}^{2}}+2sqrt{3}+{{1}^{2}}-4 right)}^{3}}+128= \ &={{left( 2sqrt{3} right)}^{3}}+128= \ &=24sqrt{3}+128 end{align}]
Ответ получился некрасивым, но это и есть искомый остаток от деления.
Ответ: $24sqrt{3}+128$.
2. Разложение на множители
Сейчас будет немного теории, которая может показаться непонятной, но далее на примерах всё встанет на свои места.
Рассмотрим ещё раз деление многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
По теореме Безу мы легко найдём остаток $r=Pleft( color{red}{a} right)$. В частности, при $Pleft( color{red}{a} right)=0$ многочлен примет вид
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
А это значит, что многочлен $Pleft( x right)$ разделился на двучлен $x-color{red}{a}$ без остатка, и мы получили разложение на множители.
Кроме того, равенство $Pleft( color{red}{a} right)=0$ означает, что число $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. И это ещё одно замечательное следствие теоремы Безу.
Следствие 2. Корни многочлена и деление
Следствие 2. Число $x=color{red}{a}$ является корнем многочлена $Pleft( x right)$ тогда и только тогда, когда $Pleft( x right)$ делится без остатка на $left( x-color{red}{a} right)$.
На практике это означает, что для разложения многочлена на множители мы просто перебираем разные числа $x=color{red}{a}$ до тех пор, пока не окажется, что $Pleft( color{red}{a} right)=0$. В этот момент многочлен перепишется в виде
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Такой перебор особенно эффективен в сочетании со схемой Горнера (см. урок «Схема Горнера»). Потому что параллельно с вычислением $Pleft( color{red}{a} right)$ мы получаем ещё и коэффициенты нового многочлена $Qleft( x right)$.
Пример 10. Обычный многочлен
Разложите на множители многочлен
[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}-11x-6]
Решение. Для наглядности отметим синим цветом коэффициенты многочлена $Pleft( x right)$:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-11} right)cdot x+left( color{blue}{-6} right)]
Составим из них таблицу для схемы Горнера:
[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline{} & {} & {} & {} & {} & {}\ end{array}]
Все коэффициенты целые, поэтому логично проверять целые $x=color{red}{a}$, начиная с самых простых и маленьких чисел:
[x=pm 1; pm 2; pm 3; ldots ]
Проверим $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline color{red}{1} & 1 & 4 & 1 & -10 & color{red}{-16}\ hline color{red}{-1} & 1 & 2 & -5 & -6 & color{green}{0}\ end{array}]
Проверка числа $x=color{red}{1}$ окончилась неудачей: остаток $r=color{red}{-16}$. Зато проверка $x=color{red}{-1}$ дала остаток $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ является корнем многочлена $Pleft( x right)$, и сам многочлен можно переписать так:
[begin{align}Pleft( x right) &=Qleft( x right)cdot left( x-left( color{red}{-1} right) right) \ &=left( {{x}^{3}}+2{{x}^{2}}-5x-6 right)left( x+1 right) end{align}]
Теперь разложим многочлен $Qleft( x right)$ по схеме Горнера. Проверим ещё раз число $x=color{red}{-1}$:
[begin{array}{r|r|r|r|r|r}{} & 1 & 3 & -3 & -11 & -6\ hline color{red}{-1} & color{blue}{1} & color{blue}{2} & color{blue}{-5} & color{blue}{-6} & color{green}{0}\ hline color{red}{-1} & 1 & 1 & -6 & color{green}{0} & {}\ end{array}]
И вновь получили $r=color{green}{0}$. Исходный многочлен примет вид
[Pleft( x right)=left( {{x}^{2}}+x-6 right){{left( x-1 right)}^{2}}]
В первой скобке стоит квадратный трёхчлен. Разложим его на множители по теореме Виета:
[{{x}^{2}}+x-6=left( x+3 right)left( x-2 right)]
Итого окончательное разложение многочлена $Pleft( x right)$:
[left( x+3 right)left( x-2 right){{left( x-1 right)}^{2}}]
Однако это было довольно простое задание: теорема Безу использовалась лишь в качестве обоснования, почему вместо $Pleft( x right)$ мы пишем $Qleft( x right)left( x-color{red}{a} right)$.
Следующее задание будет намного интереснее.:)
Пример 11. Многочлен с двумя переменными
Разложите на множители многочлен
[Pleft( x,y right)=y{{x}^{2}}+3yx+x-4y-1]
Решение. Это многочлен от двух переменных. Он квадратный относительно переменной $x$ и линейный относительно $y$. Чтобы разложить такой многочлен на множители, сгруппируем его слагаемые относительно переменной $x$:
[Pleft( x,y right)= color{blue}{y}cdot {{x}^{2}}+left( color{blue}{3y+1} right)cdot x+left( color{blue}{-4y-1} right)]
Составляем таблицу:
[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline {} & {} & {} & {}\ end{array}]
Чтобы воспользоваться теоремой Безу, нужно найти такое $x=color{red}{a}$, чтобы $r=Pleft( color{red}{a} right)= color{green}{0}$. Поскольку в роли коэффициентов выступают выражения, содержащие переменную $y$, вновь рассмотрим самые простые варианты, которые приходят в голову:
[x=pm 1; pm y]
Проверим, например, $x=color{red}{1}$:
[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline color{red}{1} & y & 4y+1 & color{green}{0}\ end{array}]
Первая же попытка привела к успеху: $r=color{green}{0}$, поэтому $x=color{red}{1}$ — крень многочлена $Pleft( x,y right)$. Разложим этот многочлен на множители согласно Следствию 2 теоремы Безу:
[Pleft( x,y right)=left( ycdot x+4y+1 right)cdot left( x-color{red}{1} right)]
В первой скобке стоит новый многочлен, линейный по $x$ и по $y$. Его уже нельзя разложить на множители, поэтому ответ окончательный:
[Pleft( x,y right)=left( xy+4y+1 right)left( x-1 right)]
Важное замечание. Строго говоря, линейность многочлена по каждой переменной ещё не означает, что его нельзя разложить на множители. Простой контрпример:
[xy-x+y-1=left( x+1 right)left( y-1 right)]
Однако в нашем случае дальнейшее применение теоремы Безу и проверки по схеме Горнера не даст никаких новых множителей.
3. Целые корни многочленов
До сих пор мы подставляли числа наугад. И если удавалось найти число $x=color{red}{a}$ такое, что $Pleft( color{red}{a} right)=0$, мы объявляли его корнем, а многочлен $Pleft( x right)$ переписывали в виде
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Однако с помощью теоремы Безу можно значительно ускорить отыскание корней, отбросив заведомо неподходящие варианты. В этом нам поможет следующее утверждение.
Следствие 3. Целочисленные корни
Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:
[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.
Обратите внимание: старший коэффициент при ${{x}^{n}}$ равен единице. Именно поэтому многочлен $Pleft( x right)$ называется приведённым. Кроме того, все коэффициенты ${{a}_{n-1}},ldots ,{{a}_{0}}$ должны быть целыми числами.
И вот тогда целые корни следует искать среди делителей свободного члена ${{a}_{0}}$.
Пример 5. Простое уравнение
Решите уравнение
[{{x}^{3}}-2{{x}^{2}}-x+2=0]
Решение. Это приведённое кубическое уравнение с целыми коэффициентами. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-2} right)cdot {{x}^{2}}+left( color{blue}{-1} right)cdot x+color{blue}{2}]
Если у него есть целые корни, то по Следствию 3 теоремы Безу все они находятся среди делителей свободного члена ${{a}_{0}}=2$. Таких делителей всего четыре:
[x=pm 1; pm 2]
Подставим эти числа в схему Горнера:
[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-2} & color{blue}{-1} & color{blue}{2}\ hline color{red}{1} & 1 & -1 & -2 & color{green}{0}\ hline color{red}{-1} & 1 & -2 & color{green}{0} & {}\ end{array}]
Уже на первом шаге мы получили $r=color{green}{0}$. Следовательно, $x=color{red}{1}$ — корень многочлена $Pleft( x right)$, и сам многочлен можно переписать так:
[Pleft( x right)=left( {{x}^{2}}-x-2 right)left( x-color{red}{1} right)]
Впрочем, если учесть третью строку таблицы, то можно вообще записать
[Pleft( x right)=left( x-2 right)left( x-left( color{red}{-1} right) right)left( x-color{red}{1} right)]
В любом случае, корни многочлена, как и корни уравнения — это числа 2, 1 и −1.
Ответ: $x=1$, $x=-1$, $x=2$.
Формула понижения степени
Итак, с помощью теоремы Безу мы можем:
- Найти целый корень многочлена;
- Разложить исходный многочлен на множители;
- Далее искать корни многочлена степени на единицу меньше.
В самом деле, если $Pleft( color{red}{a} right)=0$, тогда по Следствию 2 теоремы Безу мы переписываем многочлен $Pleft( x right)$ в виде
[Pleft( x right)=Qleft( x right)left( x-color{red}{a} right)]
Далее мы ищем корни многочлена $Qleft( x right)$, степень которого на единицу меньше $Pleft( x right)$.
Этот приём называется понижением степени. Он помогает свести исходный многочлен к квадратному, корни которого легко считаются, например, через дискриминант.
Пример 6. Среднее уравнение
Решите уравнение
[{{x}^{3}}-3{{x}^{2}}-4x+12=0]
Решение. Это уравнение третьей степени. Достаточно найти один корень — далее останется решить квадратное уравнение. Заметим, что многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-4} right)cdot x+color{blue}{12}]
является приведённым с целочисленными коэффициентами. По Следствию 3 теоремы Безу все целые корни этого многочлена содержатся среди делителей свободного члена ${{a}_{0}}=12$. Таких делителей довольно много:
[x=pm 1; pm 2; pm 3; pm 4; pm 6; pm 12]
Впрочем, нам достаточно найти всего один корень. Воспользуемся схемой Горнера:
[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-3} & color{blue}{-4} & color{blue}{12}\ hlinecolor{red}{1} & 1 & -2 & -7 & color{red}{5}\ hlinecolor{red}{-1} & 1 & -4 & 0 & color{red}{12}\ hlinecolor{red}{2} & 1 & -1 & -6 & color{green}{0}\ end{array}]
Проверка закончилась неудачей для $x=color{red}{1}$ и $x=color{red}{-1}$. Но для $x=color{red}{2}$ мы нашли то, что искали: остаток $r=color{green}{0}$. Следовательно, $x=color{red}{2}$ — корень многочлена $Pleft( x right)$.
Разложим многочлен на множители согласно теореме Безу:
[Pleft( x right)=left( {{x}^{2}}-x-6 right)left( x-color{red}{2} right)]
В первой скобке стоит квадратный трёхчлен. Его корни легко найти по теореме Виета:
[Pleft( x right)=left( x-3 right)left( x+2 right)left( x-2 right)]
Приравниваем полученное произведение к нулю и решаем уравнение: $x=3$, $x=-2$, $x=2$.
Ответ: $x=2$, $x=-2$, $x=3$.
Пример 7. Сложное уравнение
Решите уравнение
[{{x}^{4}}-{{x}^{3}}-5{{x}^{2}}+3x+2=0]
Решение. Слева приведённый многочлен с целочисленными коэффициентами, поэтому все целые корни находятся среди делителей свободного члена ${{a}_{0}}=2$:
[x=pm 1; pm 2]
Достаточно подобрать два корня — далее уравнение сведётся к квадратному. Воспользуемся схемой Горнера:
[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{-1} & color{blue}{-5} & color{blue}{3} & color{blue}{2}\ hlinecolor{red}{-1} & 1 & -2 & -3 & 6 & color{red}{-4}\ hlinecolor{red}{1} & 1 & 0 & -5 & -2 & color{green}{0}\ hlinecolor{red}{-2} & 1 & -2 & -1 & color{green}{0} & {}\ end{array}]
Получили корни $x=color{red}{1}$ и $x=color{red}{-2}$. Разложим многочлен на множители:
[left( {{x}^{2}}-2x-1 right)left( x-color{red}{1} right)left( x-left( color{red}{-2} right) right)=0]
Решим квадратного уравнение из первой скобки:
[{{x}^{2}}-2x-1=0]
Дискриминант положителен:
[begin{align} D &={{left( -2 right)}^{2}}-4cdot 1cdot left( -1 right)= \ &=4+4=8 end{align}]
Следовательно, уравнение имеет два корня:
[x=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]
Ответ: $x=1$, $x=-2$, $x=1pm sqrt{2}$.
4. Рациональные корни
До сих пор мы работали лишь с приведёнными многочленами, где старший коэффициент равен единице. Однако теорема Безу прекрасно работает и для неприведённых многочленов — при условии что все коэффициенты остаются целыми.
Рассмотрим уравнение
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.
Следствие 4. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.
Это утверждение будет доказано в конце урока. Сейчас важен практический смысл, который состоит в том, что все рациональные корни уравнения
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
имеют вид $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}$ следует искать среди делителей ${{a}_{0}}$, а $color{blue}{q}$ — среди положительных делителей ${{a}_{n}}$.
Пример 8. Простой многочлен
Найдите рациональные корни многочлена
[Pleft( x right)=2{{x}^{5}}-{{x}^{4}}+4x-2]
Решение. Делители свободного члена ${{a}_{0}}=-2$:
[p=pm 1; pm 2]
Положительные делители старшего коэффициента ${{a}_{4}}=2$:
[q=1; 2]
Возможные рациональные корни многочлена $Pleft( x right)$ по Следствию 4 теоремы Безу:
[x=pm 1; pm 2; pm {1}/{2};]
Проверять числа $x=color{red}{pm 1}$ нет смысла, поскольку все коэффициенты многочлена $Pleft( x right)$, за исключением одного, чётные. Следовательно, при подстановке нечётных чисел многочлен принимает нечётные значения, которые точно не равны нулю.
Остальные числа проверим по схеме Горнера:
[begin{array}{r|r|r|r|r|r|r}{} & color{blue}{2} & color{blue}{-1} & color{blue}{0} & color{blue}{0} & color{blue}{4} & color{blue}{-2}\ hlinecolor{red}{2} & 2 & 3 & 6 & 12 & 28 & color{red}{54}\ hlinecolor{red}{-2} & 2 & -5 & 10 & -20 & 44 & color{red}{-90}\ hline color{red}{{1}/{2};} & 2 & 0 & 0 & 0 & 4 & color{green}{0}\ hline color{red}{-{1}/{2};} & 2 & -2 & 1 & -{1}/{2}; & {17}/{4}; & color{red}{-{33}/{8};}\ end{array}]
Подошло лишь одно число: $x=color{red}{{1}/{2};}$. Следовательно, многочлен имеет лишь один рациональный корень.
Ответ: $x={1}/{2};$.
Обратите внимание: проверку дробных чисел можно прекращать, как только в строке таблицы появилась дробь. Потому что дальше это число будет лишь умножаться на новые дроби и складываться с другими целыми числами. При таких обстоятельствах получить $r=color{green}{0}$ уже невозможно.
Пример 9. Сложный многочлен
Найдите рациональные корни многочлена
[Pleft( x right)=3{{x}^{7}}+2{{x}^{6}}-5{{x}^{5}}+3{{x}^{3}}-{{x}^{2}}-7x+5]
Решение. Это многочлен с целыми коэффициентами. Делители свободного члена ${{a}_{0}}=5$:
[p=pm 1; pm 5]
Положительные делители старшего коэффициента ${{a}_{7}}=3$:
[q=1; 3]
Кандидаты в корни согласно Следствию 4 теоремы Безу:
[x=pm 1; pm 5; pm {1}/{3};; pm {1}/{5};]
Всего восемь кандидатов. Проверим их все по схеме Горнера:
[begin{array}{r|r|r|r|r|c|c|c|c}{} & color{blue}{3} & color{blue}{2} & color{blue}{-5} & color{blue}{0} & color{blue}{3} & color{blue}{-1} & color{blue}{-7} & color{blue}{5}\ hlinecolor{red}{1} & 3 & 5 & 0 & 0 & 3 & 2 & -5 & color{green}{0}\ hlinecolor{red}{-1} & 3 & 2 & -2 & 2 & 1 & 1 & color{red}{-6} & {}\ hlinecolor{red}{5} & 3 & 20 & 100 & color{red}{500} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-5} & 3 & -10 & 50 & color{red}{-250} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{1}/{3};} & 3 & 6 & 2 & color{red}{{2}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{1}/{3};} & 3 & 4 & color{red}{-{4}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{5}/{3};} & 3 & 10 & color{red}{{50}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{5}/{3};} & 3 & 0 & 0 & 0 & 3 & -3 & color{green}{0} & {}\ end{array}]
Обратите внимание: для чисел $x=color{red}{5}$ и $x=color{red}{-5}$ мы прекратили вычисления досрочно, поскольку получили явно неадекватные числа, которые дальше будут только расти.
При проверке $x=color{red}{{1}/{3};}$, $x=color{red}{-{1}/{3};}$ и $x=color{red}{{5}/{3};}$ мы в какой-то момент возникли дроби, после чего дальнейшие вычисления теряют смысл.
Итого найдены два рациональных корня: $x=color{red}{1}$ и $x=color{red}{-{5}/{3};}$. Пожалуй, это одно из самых утомительных заданий на применение теоремы Безу, которые я когда-либо решал.:)
5. Доказательства
Рассмотрим доказательства всех ключевых утверждений сегодняшнего урока.
5.1. Теорема Безу
Мы сформулировали эту теорему в самом начале урока:
Терема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x-color{red}{a}$ равен значению этого многочлена в точке $x=color{red}{a}$:
[r=Pleft( color{red}{a} right)]
Доказательство. Разделим многочлен $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
Такое представление всегда однозначно (см. урок «Деление многочленов с остатком»). Здесь многочлен $Qleft( x right)$ — неполное частное, $r$ — остаток, причём
[begin{align}deg r lt deg left( x-color{red}{a} right) &=1 \ deg r &=0 \ end{align}]
Другими словами, остаток $r$ — это просто число.
Теперь найдём значение $Pleft( x right)$ в точке $x=color{red}{a}$:
[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}-color{red}{a} right)+r=r]
Теорема Безу доказана. Однако её доказательство опирается на единственность деления с остатком.
5.2. Целочисленные корни
Целочисленные корни приведённого многочлена с целыми коэффициентами следует искать среди делителей свободного члена.
Следствие 3. Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:
[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.
Доказательство. Пусть $color{red}{b}in mathbb{Z}$ — корень многочлена $Pleft( x right)$, т.е. $Pleft( color{red}{b} right)=0$. Подставим число $x=color{red}{b}$ в формулу многочлена и получим уравнение:
[{color{red}{b}^{n}}+{{a}_{n-1}}{color{red}{b}^{n-1}}+ldots +{{a}_{1}}color{red}{b}+{{a}_{0}}=0]
Перенесём последнее слагаемое вправо, а слева из оставшихся слагаемых вынесем множитель $color{red}{b}$ за скобку:
[color{red}{b}cdot left( {color{red}{b}^{n-1}}+{{a}_{n-1}}{color{red}{b}^{n-2}}+ldots +{{a}_{1}} right)=-{{a}_{0}}]
Поскольку $-{{a}_{0}}in mathbb{Z}$, а слева стоят два целочисленных множителя, получаем, что число $-{{a}_{0}}$ делится на $color{red}{b}$. Следовательно, свободный член ${{a}_{0}}$ тоже делится на $color{red}{b}$, что и требовалось доказать.
5.3. Рациональные корни
Рассмотрим уравнение
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.
Утверждение. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения $Pleft( x right)=0$, то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.
Доказательство. Подставим число $x=color{red}{p}/color{blue}{q};$ в исходное уравнение. Поскольку $x=color{red}{p}/color{blue}{q};$ — корень, уравнение обратится в верное числовое равенство:
[{{a}_{n}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n}}+{{a}_{n-1}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n-1}}+ldots +{{a}_{1}}cdot frac{color{red}{p}}{color{blue}{q}}+{{a}_{0}}=0]
Домножим обе части на ${color{blue}{q}^{n}}$. Получим
[{{a}_{n}}{color{red}{p}^{n}}+{{a}_{n-1}}{color{red}{p}^{n-1}}color{blue}{q}+ldots +{{a}_{1}}color{red}{p}{color{blue}{q}^{n-1}}+{{a}_{0}}{color{blue}{q}^{n}}=0]
Перенесём последнее слагаемое ${{a}_{0}}{color{blue}{q}^{n}}$ вправо, а в левой части из оставшихся слагаемых вынесем множитель $color{red}{p}$ за скобку:
[color{red}{p}left( {{a}_{n}}{color{red}{p}^{n-1}}+{{a}_{n-1}}{color{red}{p}^{n-2}}color{blue}{q}+ldots +{{a}_{1}}{color{blue}{q}^{n-1}} right)=-{{a}_{0}}{color{blue}{q}^{n}}]
Слева и справа от знака равенства стоят целые числа, поскольку все слагаемые и множители являются целыми. Мы видим, что левая часть делится на $color{red}{p}$. Следовательно, правая часть тоже делится на $color{red}{p}$:
[-{{a}_{0}}{color{blue}{q}^{n}} vdots color{red}{p}]
По условию теоремы дробь $color{red}{p}/color{blue}{q};$ несократима. Следовательно, числа $color{blue}{q}$ и $color{red}{p}$ не имеют общих делителей, и единственный возможный вариант — это когда ${{a}_{0}}$ делится на $color{red}{p}$.
Аналогично доказывается, что старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$. Теорема доказана.
Вот и всё.:)
Смотрите также:
- Схема Горнера
- Деление многочленов уголком
- Теорема Виета
- Задача B3 — работа с графиками
- Метод коэффициентов, часть 2
- Нестандартная задача B2: студенты, гонорары и налоги
В данной публикации мы рассмотрим теорему Безу, с помощью которой можно найти остаток от деления многочлена на двучлен, а также, научимся применять ее на практике для решения примеров.
- Формулировка теоремы Безу
- Решение примеров
Формулировка теоремы Безу
Остаток от деления многочлена P(x) на двучлен (x-a) равняется P(a).
Pn(x) = a0xn + a1xn-1 + … + an-1x + an
Следствие из теоремы:
Число a является корнем многочлена P(x) исключительно в том случае, если многочлен P(x) без остатка делится на двучлен (x-a).
Из этого следствия вытекает следующее утверждение: множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения P(x)=0.
Решение примеров
Пример 1
Найдите остаток от деления многочлена 5x2 – 3x + 7 на двучлен (x – 2).
Решение
Чтобы найти остаток от деления, согласно теореме Безу, требуется найти значение многочлена в точке a (т.е. вместо x подставляем значение a, которое в нашем случае равняется числу 2).
5 ⋅ 22 – 3 ⋅ 2 + 7 = 21.
Т.е. остаток равен 21.
Пример 2
Используя теорему Безу выясните, делится ли многочлен 3x4 + 15x – 11 на двучлен (x + 3) без остатка.
Решение
В данном случае a = -3. Подставляем это число вместо x в многочлен и получаем:
3 ⋅ (-3)4 + 15 ⋅ (-3) – 11 = 187.
Это значит, что деление без остатка невозможно.
Пример 3
Выясните, при каком значении y, многочлен x23 + yx + 16 без остатка делится на двучлен (x + 1).
Решение
Применив теорему Безу, находим нулевой остаток от деления:
(-1)23 + y ⋅ (-1) + 16 = 0
-1 – y + 16 = 0
y = 15
Таким образом, при y, равном 15, остаток будет равен 0.
Разложение многочлена на множители. Часть 3. Теорема Безу и схема Горнера
Разложение многочлена на множители. Теорема Безу и схема Горнера
При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим, каким образом это сделать проще всего.
Как обычно, обратимся за помощью к теории.
Теорема Безу утверждает, что остаток от деления многочлена на двучлен
равен
.
Но для нас важна не сама теорема, а следствие из нее:
Если число является корнем многочлена
, то многочлен
делится без остатка на двучлен
.
Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на , где
— корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.
Эта задача распадается на две: как найти корень многочлена , и как разделить многочлен на двучлен.
Остановимся подробнее на этих моментах.
1. Как найти корень многочлена.
Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.
Здесь нам помогут такие факты:
Если сумма всех коэффициентов многочлена равна нулю, то число является корнем многочлена.
Например, в многочлене сумма коэффициентов равна нулю:
. Легко проверить, что
является корнем многочлена.
Если сумма коэффициентов многочлена при четных степенях равна сумме коэффициентов при нечетных степенях, то число
является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку
, а
— четное число.
Например, в многочлене сумма коэффициентов при четных степенях
:
, и сумма коэффициентов при нечетных степенях
:
. Легко проверить, что
является корнем многочлена.
Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.
Для приведенного многочлена степени (то есть многочлена, в котором старший коэффициент — коэффициент при
— равен единице) справедлива формула Виета:
, где
— корни многочлена
.
Если многочлен не является приведенным, то его можно сделать таковым, разделив на старший коэффициент.
Есть ещё формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.
Из этой формулы Виета следует, что если корни приведенного многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.
Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.
Рассмотрим, например, многочлен .
Для этого многочлена произведение корней равно
Делители числа :
;
;
Сумма всех коэффициентов многочлена равна , следовательно, число 1 не является корнем многочлена.
Сумма коэффициентов при четных степенях :
Сумма коэффициентов при нечетных степенях :
, следовательно, число -1 также не является корнем многочлена.
Проверим, является ли число 2 корнем многочлена: , следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен
делится без остатка на двучлен
.
2. Как разделить многочлен на двучлен.
Многочлен можно разделить на двучлен столбиком.
Разделим многочлен на двучлен
столбиком:
Есть и другой способ деления многочлена на двучлен — схема Горнера.
Посмотрите это видео, чтобы понять, как делить многочлен на двучлен столбиком, и с помощью схемы Горнера.
Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на её месте пишем 0 — так же, как при составлении таблицы для схемы Горнера.
Итак, если нам нужно разделить многочлен на двучлен
и в результате деления мы получаем многочлен
, то коэффициенты многочлена
мы можем найти по схеме Горнера:
Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число является корнем многочлена
, то остаток от деления многочлена на
равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.
Используя схему Горнера, мы «убиваем двух зайцев»: одновременно проверяем, является ли число корнем многочлена
и делим этот многочлен на двучлен
.
Пример. Решить уравнение:
1. Выпишем делители свободного члена, и будем искать корни многочлена среди делителей свободного члена.
Делители числа 24:
2. Проверим, является ли число 1 корнем многочлена.
Сумма коэффициентов многочлена , следовательно, число 1 является корнем многочлена.
3. Разделим исходный многочлен на двучлен с помощью схемы Горнера.
А) Выпишем в первую строку таблицы коэффициенты исходного многочлена.
Так как член, содержащий отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при
пишем 0. Слева пишем найденный корень: число 1.
Б) Заполняем первую строку таблицы.
В последнем столбце, как и ожидалось, мы получили ноль, мы разделили исходный многочлен на двучлен без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:
Будем делить дальше. Нам нужно найти корни многочлена . Корни также ищем среди делителей свободного члена, то есть теперь уже числа -24.
Легко проверить, что числа 1 и -1 не являются корнями многочлена
В) Продолжим таблицу. Проверим, является ли число 2 корнем многочлена :
Так степень многочлена, который получается в результате деления на единицу меньше степени исходного многочлена, следовательно и количество коэффициентов и количество столбцов на единицу меньше.
В последнем столбце мы получили -40 — число, не равное нулю, следовательно, многочлен делится на двучлен
с остатком, и число 2 не является корнем многочлена.
Идем дальше.
В) Проверим, является ли число -2 корнем многочлена . Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:
Отлично! В остатке мы получили ноль, следовательно, многочлен разделился на двучлен
без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена
на двучлен
в таблице изображены зеленым цветом.
В результате деления мы получили квадратный трехчлен , корни которого легко находятся по теореме Виета:
Итак, корни исходного уравнения :
{}
Ответ: {}
И.В. Фельдман, репетитор по математике.
Содержание:
- Формулировка теоремы Безу
- Следствия из теоремы Безу
- Примеры решения задач
Формулировка теоремы Безу
Теорема
Остаток от деления многочлена $P(x)$ на двучлен $(x-a)$ равен $P(a)$ .
Следствия из теоремы Безу
-
Число $a$ — корень многочлена $P(x)$ тогда и только тогда, когда $P(x)$ делится без остатка на двучлен $x-a$ .
Отсюда, в частности, следует, что множество корней многочлена $P(x)$ тождественно множеству корней соответствующего уравнения $P(x)=0$ .
- Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами
(если старший коэффициент равен 1, то все рациональные корни являются и целыми). - Пусть $a$ — целый корень приведенного многочлена
$P(x)$ с целыми коэффициентами. Тогда для любого целого $k$ число $P(k)$ делится на $a-k$ .
Теорема Безу дает возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого уже на
единицу меньше: если $P(a)=0$, то заданный многочлен $P(x)$ можно представить в виде:
$$P(x)=(x-a) Q(x)$$
Таким образом, один корень найден и далее находятся уже корни многочлена $Q(x)$, степень которого на единицу меньше степени исходного
многочлена. Иногда этим приемом — он называется понижением степени — можно найти все корни заданного многочлена.
Примеры решения задач
Пример
Задание. Найти остаток от деления многочлена $f(x)=3 x^{2}-4 x+6$ на двучлен $(x-1)$
Решение. Согласно теореме Безу искомый остаток равен значению многочлена в точке
$a=1$ . Найдем тогда $f(1)$, для этого значение $a=1$ подставим в выражение для многочлена $f(x)$ вместо $x$ . Будем иметь:
$$f(1)=3 cdot 1^{2}-4 cdot 1+6=3-4+6=5$$
Ответ. Остаток равен 5

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. С помощью теоремы Безу доказать, что многочлен
$f(x)=17 x^{3}-13 x^{2}-4$ делится на двучлен $x=1$ без остатка.
Решение. Указанный многочлен делится на заданный двучлен без остатка, если число
$x=1$ — корень данного многочлена, то есть имеет место равенство: $f(1)=0$ . Найдем значение многочлена в точке $x=1$ :
$$f(1)=17 cdot 1^{3}-13 cdot 1^{2}-4=17-13-4=0$$
Что и требовалось доказать
Иллюстрация теоремы Безу на примерах:
Пусть требуется, например, разделить многочлен 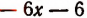
Можно предсказать, что остаток при этом делении будет равен 10. Проверим это:
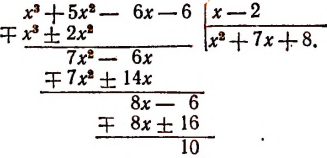
Предсказание было сделано следующим образом.
Рассматривая делитель х—2, мы видим, что в нем из независимой переменной х вычитается число 2. Это число 2 мы подставили в делимое вместо переменного х и получили 10, т. е. как раз остаток.
Действительно,
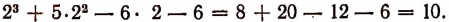
Таким образом, оказалось, что остаток от деления многочлена на х—2 равен значению делимого при х = 2.
Это правило определения остатка, сформулированное в общем виде, и будет являться теоремой Безу.
При делении многочлена 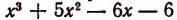
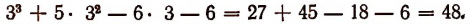
(Проверьте это непосредственным делением.)
При делении многочлена 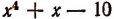
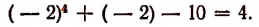
(Проверьте это непосредственным делением.)
При делении многочлена 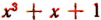
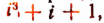
Приведенные примеры никак не могут рассматриваться как доказательства теоремы Безу: они даны лишь для того, чтобы облегчить понимание самой формулировки теоремы Безу.
Формулировка и доказательство теоремы Безу
При делении многочлена п-й степени относительно х, расположенного по убывающим степеням х, на двучлен (х — а остаток равен значению делимого при х = а
буква а может обозначать любое действительное или мнимое число, т. е. любое комплексное число).
Прежде чем доказывать теорему, сделаем несколько подготовительных пояснений.
1. В формулировке теоремы не случайно сказано: «расположенного по убывающим степеням х».
Если производить деление, расположив делимое и делитель по возрастающим степеням х, то тогда нельзя утверждать, что остаток всегда будет равен значению делимого при х = а.
Например, если многочлен 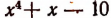
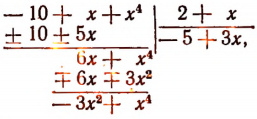
то мы никогда не получим остатка, равного числу 4, т. е. значению делимого при x = — 2.
2. Мы знаем, что существуют такие алгебраические выражения, которые теряют смысл при некоторых отдельных значениях входящих в него букв. Например, 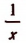
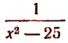
Заметим, что многочлен любой целой положительной степени никогда не теряет смысла. При всяком значении переменной он принимает определенное значение.
3. Произведение двух множителей, из которых один обращается в нуль, а другой принимает определенное значение, всегда равно нулю. Если же один множитель обращается в нуль, а другой теряет смысл, то о таком произведении нельзя говорить, что оно равно нулю. О таком произведении ничего определенного сказать нельзя. В каждом отдельном случае необходимо особое исследование.
Рассмотрим, например, произведение
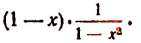
При х = 1 первый множитель обращается в нуль, а второй теряет смысл. Нельзя утверждать, что это произведение при х = 1 равно нулю.
Очевидно, что
Итак, при х = 1 само произведение 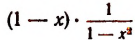
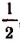
Доказательство теоремы Безу
Пусть f(x) обозначает собой произвольный многочлен n-й степени относительно переменной х, расположенный по убывающим степеням х, и пусть при делении на двучлен х — а получилось в частном q(x), а в остатке R (см. схему деления):
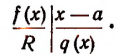
Очевидно, что q(х) будет некоторый многочлен (п — 1)-й степени относительно х, а остаток R будет величиной постоянной, т. е. не зависящей от х.
Если бы остаток R был многочленом хотя бы первой степени относительно х, то это означало бы, что процесс деления не доведен до конца. Итак, R от х не зависит
По свойству деления (делимое равно произведению делителя на частное плюс остаток) получим тождество
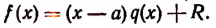
Это равенство справедливо прн всяком значении х, значит, оно будет справедливым и при х = а.
Подставляя в левую и правую части этого равенства вместо переменной х число а, получим:
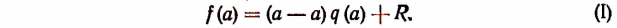
Здесь символ f(a) обозначает собой уже не f(x) т.е. не многочлен относительно х, а значение этого многочлена при х = a.
q(а) обозначает значение q(x) при х = а.
Остаток R остался таким, каким он был раньше, так как R от х не зависит.
Произведение (а — a)q(a) равно нулю, так как множитель (а — а) равен нулю, а множитель q(a) есть определенное число. (Многочлен q(x) ни при каком определенном значении х не теряет смысла.)
Поэтому из равенства (I) получим:

что и требовалось доказать.
Пример:
При делении многочлена 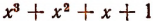
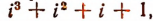
Следствия из теоремы Безу
Следствие 1. Если многочлен делится без остатка на х — а, то а необходимо будет корнем этого многочлена.
Следствие 2. Если а есть корень какого-либо многочлена, то это условие будет достаточным для делимости этого многочлена без остатка на х — а.
Эти два следствия можно объединить и выразить следующим образом:
Для делимости многочлена на x — а необходимо и достаточно, чтобы а было корнем этого многочлена.
Применения теоремы Безу
Поинтересуемся делимостью выражений вида 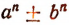
В выражении 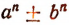
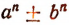
а) При делении 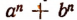
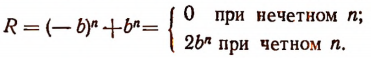
Значит, 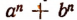
б) При делении 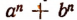
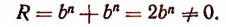
Значит, 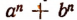
в) При делении 
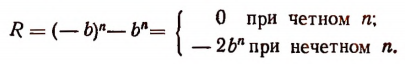
Значит, 
г) При делении 
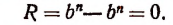
Значит, 
Другие важные применения теоремы Безу изложены в следующих главах.
Правило Горнера. Правило Горнера позволяет вычислять коэффициенты частного и остаток при делении многочлена, расположенного по убывающим степеням х, на двучлен х — а, не производя самого деления. При делении многочлена
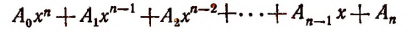
на двучлен x — а в частном получим многочлен степени (п — 1):
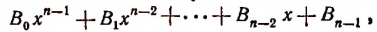
а в остатке — некоторое число R.
По свойству деления
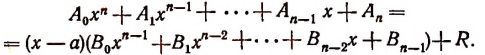
Раскрыв скобки в правой части этого равенства и объединив члены с одинаковыми степенями х, получим тот же многочлен, что и в левой части.
Приравнивая коэффициенты при одинаковых степенях х, найдем, что
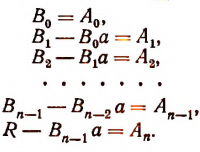
Отсюда
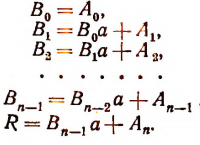
Вычисления можно располагать так: коэффициенты делимого:
коэффициенты частного и остаток:
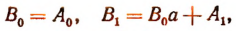
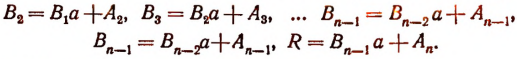
Примеры:
1. С помощью правила Горнера найти частное и остаток при делении многочлена
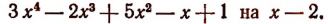
Решение:
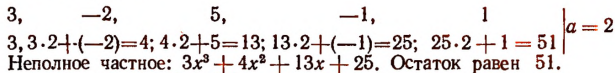
2. Разделить
Решение:
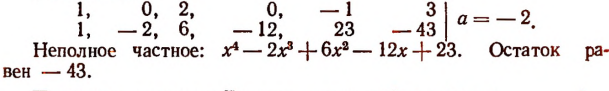
Пользуясь правилом Горнера, легко найти частное
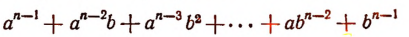
от деления
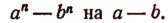
Отсюда вытекает формула
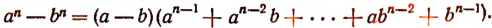
Аналогично можно получить и формулу
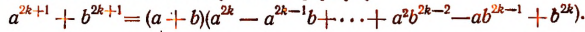
Теорема Гаусса
Если бы мы не знали никаких других чисел, кроме натуральных, то сказали бы, что уравнение 2х— 3 = 0 не имеет ни одного корня, так как нет ни одного натурального числа, которое удовлетворяло бы этому уравнению.
Уравнение 2х + 3 =0 не имеет ни одного корня в области положительных чисел.
Уравнение 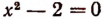
Уравнение 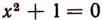
Выражение
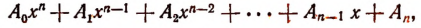
в котором х есть независимая переменная, 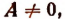
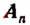
Корнем данной целой рациональной функции называется такое значение (действительное или мнимое) переменной х, при котором эта целая рациональная функция обращается в нуль.
В области действительных чисел не всякая целая рациональная функция имеет корень. Например, целая рациональная функция
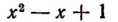
не имеет ни одного действительного корня.
В связи с этим возникает следующий важный вопрос. Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем целой рациональной функции
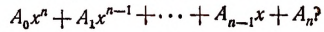
Этот вопрос на протяжении длительного исторического периода оставался неразрешенным. В 1799 году Гаусс в возрасте 22 лет дал первое строгое доказательство теоремы о существовании корня целой рациональной функции.
Теорема Гаусса гласит: Всякая целая рациональная функция с любыми комплексными коэффициентами имеет по крайней мере один корень (действительный или мнимый).
В настоящее время существует несколько различных доказательств этой фундаментальной теоремы алгебры, но все они сложны и не входят в курс элементарной алгебры.
Теорема Гаусса еще раз свидетельствует нам ту общность в решении различных вопросов, которую придает им введение в науку комплексных чисел.
Свойства целой рациональной функции
Теорема Гаусса позволяет открыть и доказать другие важные свойства целой рациональной функции.
1. Всякую целую рациональную функцию п-й степени можно представить в виде произведения коэффициента высшего члена на п линейных множителей, т. е.
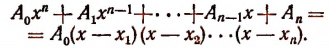
Эти линейные множители могут быть все действительными или все мнимыми и могут быть частью действительными и частью мнимыми.
Доказательство:
Функцию
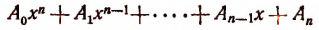
обозначим для краткости буквой М. По теореме Гаусса М имеет по крайней. мере один корень х, (действительный или мнимый). Тогда по следствию из теоремы Безу многочлен М должен делиться без остатка на 
Обозначив буквой 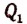
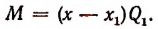
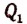
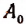
По теореме Гаусса функция 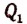
Обозначив этот корень буквой 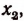
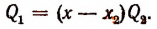
Число 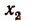
Применяя такие же рассуждения к функции 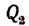
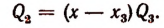
Степени функций 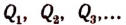
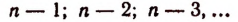
Продолжая этот процесс, мы придем к равенству

где 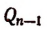
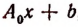
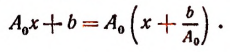
Обозначив корень функции 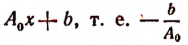
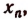
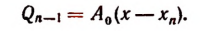
Пользуясь полученными равенствами, найдем последовательно:
что и требовалось доказать.
Из равенства (I) непосредственно видно, что числа 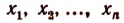
Правая часть равенства (I) не может обратиться в нуль ни при каком значении переменной х, отличном от значений
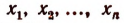
Следовательно, целая рациональная функция п-й степени не может иметь более п корней.
Если все числа 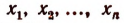
Если же среди чисел 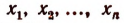
Пусть оказалось, что
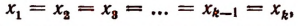
а остальные корни отличны от 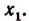
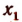
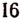

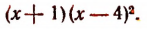
Значит, число — 1 есть простой ксрень, а число 4 есть корень кратности 2 или двукратный корень.
2. Если целая рациональная функция с действительными коэффициентами имеет комплексный корень 
Доказательство. Выражение
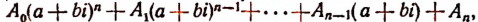
в котором 
Заменив в последнем равенстве i числом —i, получим:
Теперь допустим, что 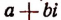
тогда окажется, что P + Qi = 0. Отсюда следует, что Р = 0 и Q = 0. Но в таком случае окажется равным нулю и выражение Р—Qi, т. е. окажется корнем целой рациональной функции (1) и число 
3. Всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима либо на действительные линейные множители, либо на действительные множители 2-й степени, либо на действительные множители, среди которых имеются и линейные и второй степени. (Доказательство 3-го свойства опускается.)
Примеры разложения целой рациональной функции с действительными коэффициентами степени выше второй на действительные неприводимые множители
Получилось разложение на действительные линейные множители.
Получилось разложение на действительные множители 2-й степени.
Получился один множитель линейный, а другой 2-й степени.
Получился один множитель линейный, а другой 2-й степени.
Теоретически доказано (как уже отмечалось), что всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима на действительные множители 1-й и 2-й степени.
Однако осуществление этого разложения не всегда достигается легко. Например, попробуем разложить на множители
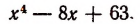
Решим эту задачу двумя способами.
(Полученные многочлены 2-й степени имеют мнимые корни, а потому неразложимы на действительные линейные множители.)
Изложенный способ носит слишком искусственный характер. Его трудно придумать.
Второй способ, изложенный ниже, будет менее искусственным.
2. Прежде всего исследуем характер корней многочлена 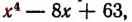
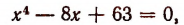
Переписав это уравнение в виде
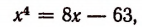
построим графики функций 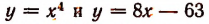
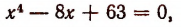
а значит, и многочлена
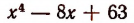
будут все мнимыми. Поэтому среди действительных множителей, на которые разлагается этот многочлен, не может быть ни одного линейного.
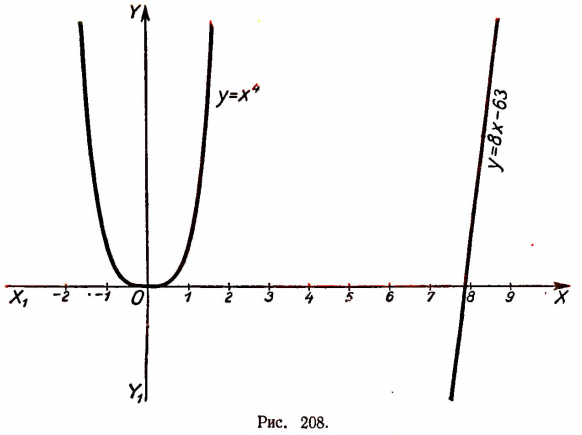
Итак, выяснено, что действительными множителями разложения многочлена 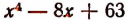
Таким образом, будем иметь, что
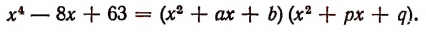
Остается определить а, b, р и q.
Перемножив многочлены, стоящие в правой части последнего равенства, получим:
Но поскольку нам необходимо, чтобы правая часть этого равенства превратилась в такой же многочлен, который стоит в левой части, потребуем выполнения следующих условий:
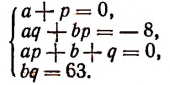
Получилась система четырех уравнений с четырьмя неизвестными a, b, р, q.
Из первого уравнения
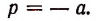
Подставив во второе и третье уравнение — а вместо р, получим систему:
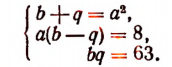
Из второго уравнения этой системы
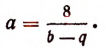
Подставив это в первое уравнение, получим систему:
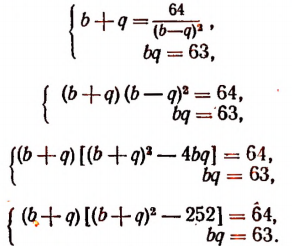
Обозначим b + q буквой z. Тогда первое уравнение последней системы примет вид:
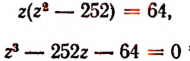
Делителями числа 64 являются: ± 1; ± 2; ± 4; ± 8; ± 16; ± 32; ± 64.
Испытывая эти делители, обнаружим, что число 16 является корнем уравнения
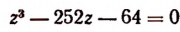
Значит, мы можем взять b + q = 16. Кроме того, bq = 63. Отсюда примем b = 7 и q = 9. Пользуясь равенством
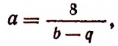
получим, что а = —4. Наконец, из равенства р = —а найдем, что р = — 4.
Теперь задача решена полностью. Мы получили:
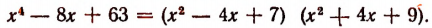
Имея это разложение, мы легко обнаруживаем все корни многочлена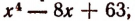
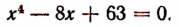
Этими корнями будут комплексные числа
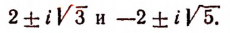
Формулы Виета
Было доказано, что целая рациональная функция разлагается иа множители по формуле:
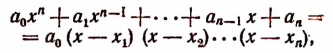
где 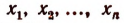
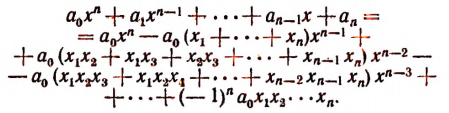
Сравнивая коэффициенты при одинаковых степенях буквы х в левой и правой частях последнего равенства, получим формулы:
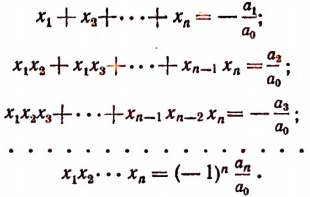
Эти формулы носят название формул Виета, по имени открывшего их замечательного французского математика Франсуа Виета. Оии связывают корни и коэффициенты целой рациональной функции. Например, для
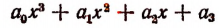
получим
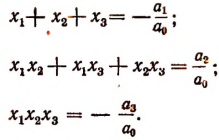
Для приведенной функции
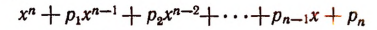
формулы Виета принимают вид:
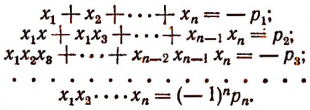
Например, для
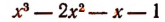
получим:
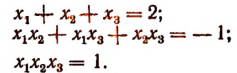
Примеры:
1. Не решая уравнения
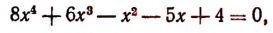
найти сумму и произведение его корней.
Решение:
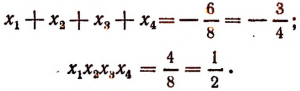
2. Пусть 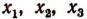
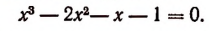
Составить новое уравнение, корнями которого были бы числа:
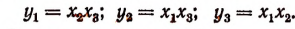
Решение:
Согласно формулам Виета
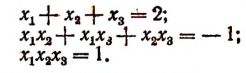
Теперь найдем значения трех выражений:
Легко видеть, что
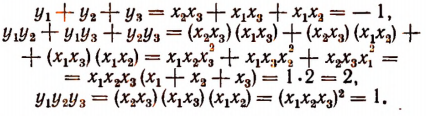
Искомым уравнением будет
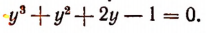
3. Сторонами треугольника являются корни уравнения
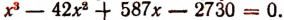
Не решая этого уравнения, найти площадь треугольника.
Решение:
Обозначим корни данного уравнения через 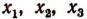
По формуле Герона
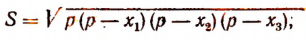
где
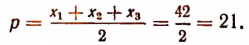
Следовательно
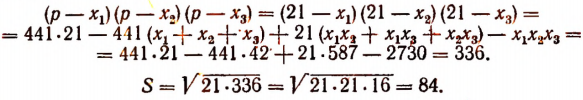
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат