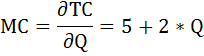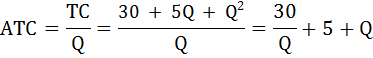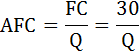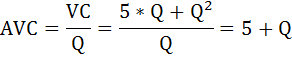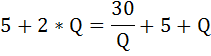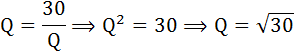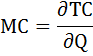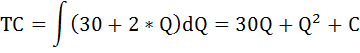Как найти минимум средних затрат

Функция общих затрат предприятия имеет вид:

TC = 30 + 5Q + Q²

Определить выражения для постоянных, переменных, предельных, средних общих, средних постоянных и средних переменных затрат как функции от Q. При каком значении Q средние общие затраты достигают минимума?

Решение:

Общие затраты предприятия складываются из постоянных и переменных затрат.

Постоянные затраты не зависят от объёма выпускаемой продукции и равны:

FC = 30.

Переменные затраты зависят от объёма выпускаемой продукции Q, поэтому из функции общих затрат выписываем все слагаемые, содержащие Q:

VC = 5Q + Q²

Продифференцируем функцию общих затрат и найдём выражение для предельных затрат:

Средние общие затраты найдём по формуле:

Средние постоянные затраты равны:

Средние переменные затраты равны:

или

AVC = ATC – AFC = 5 + Q

Средние общие затраты достигают минимума при равенстве предельным затратам:

MC = ATC

Источник

Минимальные средние издержки

Задача

В подборках

Раздел

Темы

Сложность

Автор

10.11.2010, 14:05 ()

18.06.2015, 23:52

Функция общих издержек фирмы имеет вид $ТС (Q)= Q (2Q+1)+32$ , где
ТС – издержки, измеряемые в рублях. Найди минимальные средние издержки
фирмы.

Решение и ответ

Пожалуйста, помогите решить)

AC=TC/Q => AC=2Q+1+32/Q
AC-> min
AC`=2-32/Q2= (2Q2-32)/Q2=0
=>(Q-4)(Q+4)=0
Рисуем знаковый портрет функции и доказываем, что Q=4 является точкой минимума. Следовательно, при объеме выпуска,равном 4ем единицам, достигается минимум средних издержек.
=> ACmin=AC(4)=17.
Советую проверить решение,потому как оочень хочу спать и,вполне возможно, могла сделать ошибку)

Да, у меня такой же ответ)

можно решать еще и другим способом:
так как мы знаем, что график МС пересекает график АС в точке минимума, следовательно
MC(Q)=AC(Q);
Mc(Q)=TC`(Q);
4Q+1=2Q+1+32/Q
Решая уравнение, получим такой же ответ.

)))А я тут загнула через производную)
Да. Тем более,возможно, Роман еще не успел пройти производную. Так что ваш способ должен быть намного проще для него

Кстати, Радмила, вы написали следующее:
Mc(Q)=TC`(Q);
Это не совсем верно,так как TC`(Q) не равно AC(Q). )

я имела в виду, что равенство выполняется в точке минимума АС.

а так , конечно, в общем случае МС не равны АС)))

Радмила, пожалуйста, объясните как вы получили: $4Q+1$ (MC(Q)).

Возможно, вы не прошли еще прозводной? тогда пока можно пользоваться только формулами.
MC(Q) — это производная от TC(Q),
$f(x)= k*x^{n},{f}'(x)=k*n*x^{n-1}$

$TC(q)=2q^{2}+q+32,{TC}'(q)=2*2q^{2-1}+1*q^{1-1}=4q+1$

Гули, я разобрался и в вашем решении. На самом деле я знал понятие и смысл производной, знал про экстремумы, но я формул не знал;). Спасибо!

Источник

Изокоста.Правило минимиз.Издержек.

Расходы
фирмы на факторы производства можно
описать уравнением: TC=P_LL+P_KK,
где:
TC
– совокупные затраты в денежном
выражении; P_L
, P_K
– цены единицы труда и капитала; L,
K
– затраты труда и капитала.

Фирма
может иметь одинаковый размер совокупных
издержек при различном сочетании
факторов производства. Данную ситуацию
изобразим графически, на вертикальной
оси отложим значения затрат капитала,
на горизонтальной – затрат труда.
Область значений К определяется как
TC/P_K
, а значений L
как TC/P_L(рис.
7.4.1.).

Рис.
7.4.1.- Изокоста Прямая линия, которая
показывает равенство совокупных издержек
в денежном выражении при различном
сочетании двух факторов производства,
называется изокостой.

Тангес
угла наклона (а) изокосты равен отношению
цен факторов производства, а ее
отдаленность от начала координат
определяется величиной общих издержек.
Совокупность изокост, отражающих разную
величину общих издержек при заданных
ценах на труд и капитал, представляет
собой семейство
изокост.
Наклон любой из семейства изокост равен:
P_L/Р_k
.

С
овместим
на одном графике изокванту и семейство
изокост (рис. 7.5.2.).

Рис.
7.5.2- Определение минимальных издержек
для заданного объема выпуска.

Точка
касания изокванты с наименьшей из
доступных ей изокост показывает
минимально возможный размер совокупных
затрат для заданного объема выпуска.
Изокванта касается одной из изокост в
точке М, в которой наклон изокванты и
изокосты одинаковы. Так как наклон
изокванты определяется MRTS_LK
, а наклон изокосты отношением P_LиР_К
, то условие
минимизации издержек:

.

Как
известно,,то
можно записать:
,или
.

Минимальные
издержки для заданного объема выпуска
фирма получит, если
обеспечит равенство взвешенных предельных
продуктов каждого ресурса.

22.Издержки произ-ва в краткоср.Периоде.Пост.И перем.Издержки. Общие и средние изд. Пред.Издержки.

Для
анализа издержек фирмы в краткосрочном
периоде их делят на постоянные и
переменные. Издержки, величина которых
не изменяется с изменением объема
производства, получили название
постоянных
издержек.
К ним относят амортизацию зданий и
сооружений, арендную плату, страховые
взносы, заработную плату высшего
управленческого персонала, расходы на
НИОКР и т.д. Издержки, величина которых
зависит от объема производства, называются
переменными
издержками.
Переменные издержки – это затраты на
сырье, топливо, энергию, заработную
плату рабочих, транспортно-складские
услуги и т.д. В отличие от постоянных
издержек величиной переменных издержек
администрация фирмы может управлять,
изменяя объем выпуска продукции. В
аналитических целях выделяют общие,
средние и предельные издержки.

Общие
издержки
фирмы для данного объема производства
представляют собой сумму постоянных и
переменных издержек. Они определяются
по формуле: TC
= FC
+ VC,
где:
TC
(total
costs)
– общие издержки; FC
(fixed
costs)
– постоянные издержки; VC
(variable
costs)
– переменные издержки.

Средние
издержки
– издержки в расчете на единицу продукции
для данного объема производства. Их
можно определить по формуле:
,
где: АС
(average
costs)
– средние издержки; Q
–
объем выпуска. Средние издержки можно
разграничить на средние постоянные
(AFC)
и средние переменные издержки (AVC).
Средние
постоянные издержки
определяются делением постоянных
издержек на объем выпуска:
.
Средние
переменные издержки
равны частному от деления переменных
издержек на объем выпуска:
.
Для определения выгодности выпуска
конкретного вида продукции, фирма
сравнивает средние издержки с ценой
продукции. Если средние издержки меньше
цены фирме есть смысл производить
данный товар, т.к. она сможет возместить
затраты на производство и получить
прибыль.

Для
принятия решения об оптимальном объеме
выпуска фирма определяет предельные
издержки. Предельные
издержки
(marginal costs)
– это затраты на производство
дополнительной единицы продукции. Они
показывают изменение величины общих
издержек при увеличении объема выпуска
на одну единицу продукции. Определяются
предельные издержки по формуле:
,где:
ТС
– величина изменения общих издержек;
Q
–увеличение объема выпуска на единицу
продукции.

Рост
объема производства сопровождается
увеличением переменных и общих издержек.
Графическое изображение кривых средних
и предельных издержек выявляет важные
зависимости (рис. 7.7.1.). Средние постоянные
издержки (AFC)
с увеличением объема производства
уменьшаются, но при этом остаются
положительной величиной. Средние
переменные издержки (AVC)
вначале с ростом производства уменьшаются,
при определенном объеме производства
достигают своего минимума, а затем
начинают расти. Это обусловлено тем,
что до тех пор, пока увеличение переменного
ресурса ведет к повышению эффективности
производства, переменные издержки в
расчете на единицу продукции снижаются.
При превышении переменным ресурсом
оптимального размера начинает действовать
закон убывающей предельной производительности
ресурса, и средние переменные издержки
начинают

р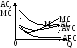асти.
Предельные издержки (MC)
на стадии освоения производства велики,
с ростом эффективности производства
снижаются. При превышении оптимального
размера переменным ресурсом, предельные

издержки
растут.

ис 7.7.1- Кривые средних и предельных
издержек.

Кривая
предельных издержек МС пересекает
кривую АС в точке М, когда средние
издержки имеют минимальную величину.
Данная зависимость между предельными
и средними издержками называется
правилом средних и предельных издержек,
суть которого в том, что фирма имеет
объем выпуска, который позволяет
минимизировать издержки, когда МС = АС.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задача №1. Расчёт экономической прибыли конкурентной фирмы

Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:

ТС = 140 + 10 × Q + 40 × Q².

При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.

Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы?

Решение:

Наличие в составе общих затрат фиксированных (постоянных) затрат (FC = 140) свидетельствует о том, что речь идёт о краткосрочном периоде.

Найдём объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде имеет вид:

Р = МС = МR = AR.

Определим функцию предельных издержек фирмы: найдём производную общих издержек.

МС = (ТС)’ = 10 + 80 × Q.

Приравняем эту функцию к цене равной 250.

10 + 80 × Q = 250

80 × Q = 240

Q = 3

Вычислим прибыль фирмы при объёме выпуска равном 3 по формуле:

П = TR — TC = P × Q — TC = 250 × 3 — (140 + 10 × 3 + 40 × 3²) = 220 ден. ед.

В долгосрочном периоде наличие неотрицательной экономической прибыли будет привлекать в отрасль новые фирмы.

Задача № 2. Определение рыночной цены и отраслевого выпуска продукции

В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями

ТС =Q³ — 36*Q² + 384*Q,

где

Q — объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие.

Решение:

В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство:

P = MC = MR = AR = minAC.

Найдём функцию средних издержек каждой фирмы по следующей формуле:

АС = ТС / Q = Q² — 36*Q + 384

Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю.

2*Q — 36 = 0

Q = 18

AC(18) = 18² — 36*18 + 384 = 60

Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60.

Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут:

Q_отр. = 18*130 = 2340 тысяч штук

Задача № 3. Определение рыночной цены в долгосрочном периоде

Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q³ — 38*Q² + 418*Q. Определите цену на этом рынке в долгосрочном периоде.

Решение:

В долгосрочном периоде цена в условиях соверешенной конкуренции устанавливается на уровне минимума средних затрат. При этом фирма совершенный конкурент получает нулевую экономическую прибыль.

Условие равновесия на рынке будет иметь вид:

Р = МС = МR = AR = min AC

Найдём средние затраты фирмы по формуле:

АС = ТС / Q = Q² — 38*Q + 418

Определим минимум функции средних затрат. Для нахождения экстремума функции приравняем к нулю её производную:

АС’ = 2*Q — 38

2*Q — 38 = 0

Q = 19

При выпуске Q = 19 средние затраты будут равны:

АС = 19² — 38*19 + 418 = 57.

Таким образом, цена в долгосрочном периоде будет равна 57.

Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка

Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют

0,5*Q³ — 15*Q² + 300*Q + 250 000.

При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде?

Решение:

В краткосрочном периоде фирма совершенный конкурент уйдёт с рынка, если цена окажется меньше минимума её средних переменных издержек: Р < min AVC.

Найдём переменные издержки фирмы, а точнее запишем функцию переменных издержек:

VC = 0,5*Q³ — 15*Q² + 300*Q

Теперь определим функцию средних переменных издержек по формуле:

АVC = VC / Q = 0,5*Q² — 15*Q + 300

Найдём экстремум этой функции, приравняв к нулю её производную.

Q — 15 = 0

Q = 15.

При объёме производства Q = 15 средние переменные издержки будут минимальными.

АVC(15) = 0,5*15² — 15*15 + 300 = 187,5

Это так называемая точка закрытия фирмы. Фирма совершенный конкурент уйдёт с рынка, если цена упадёт ниже этой точки в краткосрочном периоде.

При Р < 187,5 фирме становится невыгодным работать на этом рынке в краткосрочном периоде.

Задача № 5. Расчёт объёма выпуска, максимизирующего прибыль фирмы

Функция издержек фирмы ТС = Q² — Q + 3, где Q — объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.

Решение:

По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.

Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.

Найдём предельные издержки фирмы по формуле:

МС =(TC)’= 2Q — 1

Найдём объём выпуска продукции, максимизирующий прибыль фирмы.

Цена по условию равна Р = 7.

Р = МС

7 = 2Q — 1

Q = 4

Задача №6. Расчёт объёма производства в краткосрочном периоде

В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q² + 10 * Q + 100. Найти её объём производства в краткосрочном периоде.

Решение:

Фирма выберет такой объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли: МС = MR.

На рынке совершенной конкуренции предельный доход равен цене: MR = P.

Отсюда следует, что цена равна предельным издержкам: P = MC.

Найдём предельные издержки. Предельные издержки в непрерывном случае (т.е. когда общие издержки заданы функцией) равны производной от функции общих издержек:

Функция предельных издержек будет иметь вид:

МС = Q + 10
P = MC
30 = Q + 10
Q = 20 — оптимальный объём производства фирмы.

Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет общие затраты

ТС = 800 + 40*Q + 2*Q²

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли фирмы имеет вид:

П = TR — TC = P*Q — TC

По условию максимально возможная прибыль равна 1000.

P*Q — (800 + 40*Q + 2*Q²) = 1000

Найдём цену.

Условие максимизации прибыли на рынке совершенной конкуренции имеет вид:

Р = МС = MR = AR

Так как Р = МС, а МС = ТС’ = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим:

(40 + 4*Q)*Q — (800 + 40*Q + 2*Q²) = 1000

40*Q + 4*Q² — 800 — 40*Q — 2*Q²— 1000 = 0

2*Q² = 1800

Q²= 900

Q_1,2 = ±30

Так как отрицательный корень экономического содержания не имеет, берём Q = 30.

Тогда цена будет равна:

Р = 40 + 4*30 = 160

Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде

Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют:

Q³ – 16*Q² + 400*Q.

а) При каком значении Q средние затраты достигают минимума?

б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде?

Решение:

а) Найдём функцию средних затрат по формуле:

АС = ТС / Q = (Q³ – 16*Q² + 400*Q) / Q = Q² – 16*Q + 400

Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю.

AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16
2*Q – 16 = 0
Q = 8

При Q = 8 средние затраты достигают минимума.

б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие:

Р = МС = MR = minАС

Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат:

minAC(Q=8) = 82 – 16*8 + 400 = 336

Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде.

Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль

Спрос на продукцию конкурентной отрасли:

Q_d = 55 – P

Предложение:

Q_s = 2P – 5

Если у одной из фирм отрасли восходящий участок кривой предельных издержек:

МС = 3Q + 5

При каких цене и объёме производства фирма максимизирует прибыль?

Решение:

Найдём цену равновесия. Приравняем функцию спроса и предложения:

Qd = Qs
55 – P = 2P – 5
3 * Р = 60
Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию.

Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат.

МС = Р
3Q + 5 = 20
Q = 5 – объём производства, при котором прибыль фирмы будет максимальной.

Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет предельные затраты:

МС = 30 + 2 × Q

при фиксированных затратах, равных 500 денежным единицам.

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли имеет вид:

П = TR – TC = P*Q – TC

Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.

где

С – константа, равная величине фиксированных затрат, которые по условию равны 500.

Таким образом функция общих затрат имеет вид:

ТС = Q² +30*Q + 500

Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR

Воспользуемся тем, что:

Р = МС

По условию задачи:

МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q

Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.

(30 + 2 * Q) * Q – (Q² +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40

Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.

Тогда рыночная цена будет равна:

Р = 30 + 2 * 40 = 110.

Источник

��

� 2-� ��. �� «�� », ��-��, 2004.

8.3. ��

�� , �� , � ��, �� .

� �� (FC; fixed cost � ��.) �� , ��, ��, ��-�� , �� , �� . �� , �� «��» ��. � �� (VC; variable cost � ��.) ��, �� , �� , ��, �� .

�� , �� :

STC(Q) = FC+VC(Q),

�� STC(Q) � �� Q �� ; FC � �� ; VC(Q) � �� Q �� .

�� . 8.5,� �� STC, VC � FC �� . �� (STC) �� , �� , �� . 8.3,�, � �� FC �� ₀ �� . 8.3,6. �� , �� . 8.5 �� STC, �� , �� FC, � �� , �� FC � �� STC. �� STC �� , �� FC � VC. ��, �� VC �� .

�� , �� , �� , ��, ��, �� (��) ��.

�� :

SATC = STC/Q = (FC/Q) + (VC/Q) = AFC + SAVC, (8.5)

�� SATC — �� Q �� ; AFC — �� Q �� ; SAVC — �� Q �� .

�� . �� FC = const, a AFC = FC/Q, �� AFC � Q = FC = const. ��, �� AFC �� (��. 8.5). �� , �� . �� .

�� STC � VC �� . 8.5 �� (SATC) � �� (SAVC) ��. �� , �� , �� , �� STC �� VC, �� . ��, �� Q₃ � Q₂ (��. 8 5). ��, �� .

SATC(Q₃) = min,
SAVC(Q₂) = min.

��, �� , �� . � �� . 8.5 ��, ��> �� , �� STC � V� ��. �� SMC �� SAVC � SATC � �� ’ � �’ ��.

�� , �� (8.3) �� :

MC = dTC/dQ = dVC/dQ, (8.6)

�� , �� �� �� .

�� (��. 8.5).

1 �� SATC �� SAVC ��, �. �. dSATC/dQ < 0 �� dSAVC/dQ < 0, �� , SMC < SATC �� SMC < SAVC (�� SATC � SAVC �� ’ � �1).

2. �� SATC �� SAVC ��, �.�. dSATC/dQ > 0 �� dSAVC/dQ > 0, �� , SMC > SATC �� SMC > SAVC (�� SATC � SAVC �� ’).

3. SATC � SAVC �� , �.�. dSATC/dQ = 0 �� dSAVC/dQ = 0, �� , SM� = SATC �� SMC = SAVC (�� ’ � �’)

4. SAV� �� , �� S��, �� , �� AFC �� SAVC (�� ’ �� ’).

—

Источник

Решение:

Минимальные средние издержки

В подборках

Раздел

Темы

Сложность

Автор

Комментарии

Изокоста.Правило минимиз.Издержек.

22.Издержки произ-ва в краткоср.Периоде.Пост.И перем.Издержки. Общие и средние изд. Пред.Издержки.

Задача №1. Расчёт экономической прибыли конкурентной фирмы

Решение:

Задача № 2. Определение рыночной цены и отраслевого выпуска продукции

Решение:

Задача № 3. Определение рыночной цены в долгосрочном периоде

Решение:

Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка

Решение:

Задача № 5. Расчёт объёма выпуска, максимизирующего прибыль фирмы

Решение:

Задача №6. Расчёт объёма производства в краткосрочном периоде

Решение:

Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Решение:

Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде

Решение:

Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль

Решение:

Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Решение:

Не пропустите также: