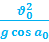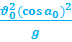1) найти радиус кривизны траектории в наивысшей точке полета.

2)найти радийс кривизны траектории в начальной точке полета.
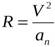
3) найти радиус траектории.
Центр масс твёрдого тела движется так же как двигалась бы материальная точка, масса которой равна массе тела, под действием внешних сил, приложенных к данному телу.
Тело состоит из нескольких элементов. Уравнение i-го элемента массой m записывается так:
Где Fi внешняя сила, а ∑Fik это сумма внутренних сил, действующих на i-ый элемент со стороны всех других элементов.
Сложим все аналогичные уравнения для всех элементов. Т.к. Fik = -Fki третьему закону Ньютона, то их сумма равна нулю.
После сложения получим:
Устойчивое равновесие — это равновесие, при котором, тело, выведенное из положения равновесия, вернётся в то же положение.
Неустойчивое равновесие — если тело, после смещения, не вернётся в это положение.
Скорость точки, движущейся по окружности ,часто называют Линейной скоростью ,чтобы подчеркнуть ее отличие от угловой скорости. Между линейной скоростью точки, обращающейся по окружности, и ее угловой скоростью существует связь. При равномерном движении точки по любой траектории модуль скорости равен s/∆t
Точка A, движущаяся по окружности радиуса R,за время ∆t проходит путь равный дуге A1A2
S=A1A2=∆ϕR .Модуль линейной скорости движения v= s/∆t ==∆ϕR/∆t=ωR
Итак , модуль линейной скорости точки, движущейся по окружности, равен произведению угловой скорости на радиус окружности :
Эта формула справедлива как для равномерного, так и для неравномерного движения точки по окружности.
Модуль ускорения точки, движущейся по окружности, можно выразить через угловую скорость тела и радиус окружности. Так как a=v²/R и v= ωR


















Очевидно, что модуль ускорения при равномерном движении точки по окружности есть постоянная величина, так как U и r не изменяются при движении
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9614 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
1.59. Радиус кривизны траектории в точке бросания: 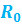
1.60. Радиус кривизны траектории в точке максимальной высоты А :

Замечание1: радиус кривизны 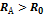
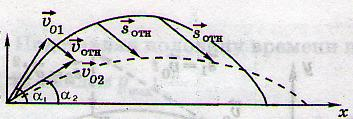
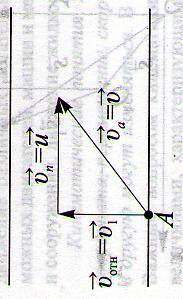
Как будут двигаться относительно друг друга два тела брошенные одновременно под разными углами к горизонту?
1.61.
… —второе тело относительно первого тела будет двигаться равномерно и прямолинейно, и вектор перемещения, соединяющий тела, в любой момент времени будет параллелен вектору относительной скорости:

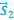
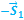

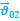
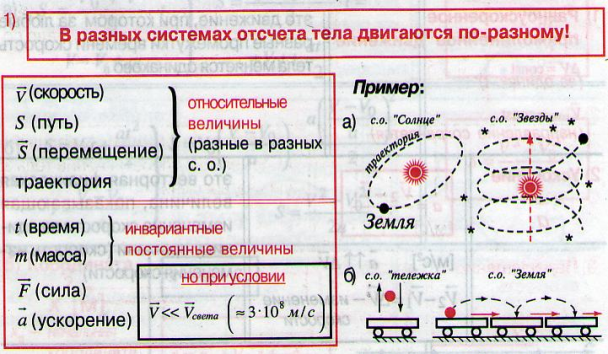
Относительность механического движения
§ 1.6.
1.63. Относительность скорости.
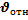
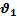
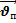
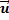
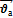
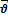


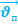
…- формула сложения скоростей



…- формула сложения перемещений.
Замечание: формулы (1) и (2) формулы преобразования Галилея.
Пойдем в обратном порядке.
gh=3/4*(2/3*(g*t)^2);
t=(3*h/*g)^0,5, где g – ускорение свободно падения;
t
0,3 c
А Митин Андрей, по-моему, проврался: в выражении t=2/(h*(8*g*h/5)^0.5) проблемы с размерностью.
2) Аппроксимируем движение точки равномерным движением по окружности.
v=w*R; a=w^2*R; m=p/v=p/(w*R);
F=m*a=(p*w^2*R)/(w*R)=p*w;
F=0,1*0,5*pi Н=0,05*pi Н, где pi – число пи.
1) Тут пока выкладки получаются громоздкие – утомительно писать в подобном окне. Может, потом чего-нибудь попроще придумаю. Но ответ такой: максимальны радиус в крайних точках траектории (начальной и конечной моменты движения), а минимальный – в точке, что делит траекторию пополам и в которой движение горизонтально.
Конечные соотношения:
R(t)=v(t)^3/(g*v(0)*cos(A)), где g – ускорение свободного падения.
Радиус кривизны траектории
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1.
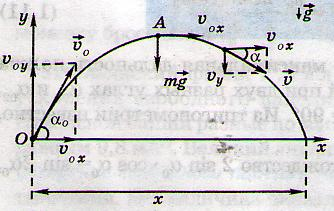
Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.
К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и
. Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м,
м,
м.
Задача 2.
Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б)
.
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и
:
Откуда .
Ответ: а) , б)
.
Для
определения минимального радиуса
кулачка Rmin
строится дополнительная диаграмма
методом исключения угла φ
в
масштабе
по
данным таблицы 2.
Для
этого проводим взаимно перпендикулярные
оси. Ось ординат обозначим через S,
а
ось абсцисс через S´.
По оси S
производим разметку пути толкателя. В
направлении, перпендикулярном движению
толкателя откладываем для каждого
положения величины S´
вправо при движении толкателя вверх.
Построенные точки соединяем плавной
кривой.
Строим
вторую половину диаграммы, откладывая
величины S´
влево при движении толкателя вниз.
По
диаграмме
определяем
допустимую область центров вращения
кулачка. Для этого из концов отрезков
максимальных значений S´
проводим лучи под углом υдоп=30°
к направлению движения толкателя.
Эти лучи пересекаются
в точке О1,
которая определяет положение оси
вращения кулачка при его минимальных
размерах.
ОО1
представляет собой минимальный радиус
профиля кулачка Rmin=
ОО1=
100 мм. Этот размер берется прямо с чертежа,
так как диаграмма
была построена в масштабе
3.4 Построение профиля кулачка
Начинаем построение
профиля кулачка (без ролика).
В произвольной
точки О (ось вращения кулачка) проводим
окружность радиусом Rmin=
100 мм., то есть построение производим в
масштабе
.
Через ось О проводим линию 0 – 0 движение
толкателя.
В соответствии с
разметкой фазовых углов на графике
S»
откладываем, начиная от действительной
линии движения толкателя, в направлении
противоположном вращению кулачка,
фазовые углы φу=170°
и φв=170°.
Отмечаем на
окружности Rmin
точки 6,12.
Делим
фазовые углы на шесть равных частей
(каждая часть равна 28,33°).
Точки деления на окружности Rmin
соединяем радиусами (лучами) с центром
вращения кулачка – точкой О.
От
окружности радиуса Rmin
вдоль этих радиусов от соответствующей
точки откладываем перемещения толкателя
из таблицы 2 для
.
Эти перемещения
показаны толстыми линиями.
Соединяем полученные
точки плавной кривой, получаем центровой
(теоретический) профиль кулачка. Этот
профиль является рабочим профилем
кулачка с толкателем без ролика.
Определяем
минимальный радиус кривизны центрового
профиля кулачка ρmin
как радиус вписанной окружности выпуклого
участка профиля кулачка, где кривизны
окажется наибольшей. На этом участке
произвольно выбираем три точки 3,4,5 и
соединяем их двумя хордами. В середине
хорд восстанавливаем к ним перпендикуляры,
точку пересечения которых М принимаем
за центр вписанной окружности. Получаем
ρmin=155
мм. в масштабе М 10:1.
Действительный
профиль кулачка найдем как эквидистантную
кривую, отстоящую от центрального
профиля на расстоянии, равном радиусу
ролика.
Радиус ролика
выбирается наименьшим из условий:
Принимаем
rp=4
мм.
Для
получения действительного (рабочего)
профиля кулачка на его центровом профиле
выбираем ряд точек, из которых проводим
окружности радиусом, равным радиусу
ролика rp.
Огибающая этих
окружностей (внутренняя) и является
действительным (рабочем) профилем
кулачка.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
This article is about the general mathematical concept. For its optical applications, see Radius of curvature (optics).
In differential geometry, the radius of curvature (Rc), R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.[1][2][3]
Definition[edit]
In the case of a space curve, the radius of curvature is the length of the curvature vector.
In the case of a plane curve, then R is the absolute value of[3]
where s is the arc length from a fixed point on the curve, φ is the tangential angle and κ is the curvature.
Formula[edit]
In 2D[edit]
If the curve is given in Cartesian coordinates as y(x), i.e., as the graph of a function, then the radius of curvature is (assuming the curve is differentiable up to order 2):
and |z| denotes the absolute value of z.
Also in Classical mechanics branch of Physics Radius of curvature is given by (Net Velocity)²/Acceleration Perpendicular
If the curve is given parametrically by functions x(t) and y(t), then the radius of curvature is
Heuristically, this result can be interpreted as[2]
In n dimensions[edit]
If γ : ℝ → ℝn is a parametrized curve in ℝn then the radius of curvature at each point of the curve, ρ : ℝ → ℝ, is given by[3]
.
As a special case, if f(t) is a function from ℝ to ℝ, then the radius of curvature of its graph, γ(t) = (t, f(t)), is
Derivation[edit]
Let γ be as above, and fix t. We want to find the radius ρ of a parametrized circle which matches γ in its zeroth, first, and second derivatives at t. Clearly the radius will not depend on the position γ(t), only on the velocity γ′(t) and acceleration γ″(t). There are only three independent scalars that can be obtained from two vectors v and w, namely v · v, v · w, and w · w. Thus the radius of curvature must be a function of the three scalars |γ′(t)|2, |γ″(t)|2 and γ′(t) · γ″(t).[3]
The general equation for a parametrized circle in ℝn is
where c ∈ ℝn is the center of the circle (irrelevant since it disappears in the derivatives), a,b ∈ ℝn are perpendicular vectors of length ρ (that is, a · a = b · b = ρ2 and a · b = 0), and h : ℝ → ℝ is an arbitrary function which is twice differentiable at t.
The relevant derivatives of g work out to be
If we now equate these derivatives of g to the corresponding derivatives of γ at t we obtain
These three equations in three unknowns (ρ, h′(t) and h″(t)) can be solved for ρ, giving the formula for the radius of curvature:
or, omitting the parameter t for readability,
Examples[edit]
Semicircles and circles[edit]
For a semi-circle of radius a in the upper half-plane
An ellipse (red) and its evolute (blue). The dots are the vertices of the ellipse, at the points of greatest and least curvature.
For a semi-circle of radius a in the lower half-plane
The circle of radius a has a radius of curvature equal to a.
Ellipses[edit]
In an ellipse with major axis 2a and minor axis 2b, the vertices on the major axis have the smallest radius of curvature of any points, R = b2/a; and the vertices on the minor axis have the largest radius of curvature of any points, R = a2/b.
The ellipse’s radius of curvature, as a function of parameter t
[4]
And as a function of θ
Where e is the eccentricity of the ellipse and is given by:

Applications[edit]
- For the use in differential geometry, see Cesàro equation.
- For the radius of curvature of the earth (approximated by an oblate ellipsoid); see also: arc measurement
- Radius of curvature is also used in a three part equation for bending of beams.
- Radius of curvature (optics)
- Thin films technologies
- Printed electronics
- Minimum railway curve radius
- AFM probe
Stress in semiconductor structures[edit]
Stress in the semiconductor structure involving evaporated thin films usually results from the thermal expansion (thermal stress) during the manufacturing process. Thermal stress occurs because film depositions are usually made above room temperature. Upon cooling from the deposition temperature to room temperature, the difference in the thermal expansion coefficients of the substrate and the film cause thermal stress.[5]
Intrinsic stress results from the microstructure created in the film as atoms are deposited on the substrate. Tensile stress results from microvoids (small holes, considered to be defects) in the thin film, because of the attractive interaction of atoms across the voids.
The stress in thin film semiconductor structures results in the buckling of the wafers. The radius of the curvature of the stressed structure is related to stress tensor in the structure, and can be described by modified Stoney formula.[6] The topography of the stressed structure including radii of curvature can be measured using optical scanner methods. The modern scanner tools have capability to measure full topography of the substrate and to measure both principal radii of curvature, while providing the accuracy of the order of 0.1% for radii of curvature of 90 meters and more.[7]
See also[edit]
- Base curve radius
- Bend radius
- Degree of curvature (civil engineering)
- Osculating circle
- Track transition curve
References[edit]
- ^ Weisstien, Eric. «Radius of Curvature». Wolfram Mathworld. Retrieved 15 August 2016.
- ^ a b Kishan, Hari (2007). Differential Calculus. Atlantic Publishers & Dist. ISBN 9788126908202.
- ^ a b c d Love, Clyde E.; Rainville, Earl D. (1962). Differential and Integral Calculus (Sixth ed.). New York: MacMillan.
- ^ Weisstein, Eric W. «Ellipse». mathworld.wolfram.com. Retrieved 2022-02-23.
- ^ «Controlling Stress in Thin Films». Flipchips.com. Retrieved 2016-04-22.
- ^ «On the determination of film stress from substrate bending : Stoney’s formula and its limits» (PDF). Qucosa.de. Retrieved 2016-04-22.
- ^ Peter Walecki. «Model X». Zebraoptical.com. Retrieved 2016-04-22.
Further reading[edit]
- do Carmo, Manfredo (1976). Differential Geometry of Curves and Surfaces. ISBN 0-13-212589-7.
External links[edit]
- The Geometry Center: Principal Curvatures
- 15.3 Curvature and Radius of Curvature
- Weisstein, Eric W. «Principal Curvatures». MathWorld.
- Weisstein, Eric W. «Principal Radius of Curvature». MathWorld.
2018-01-18
Тело бросают со скоростью $v_{0} = 10 м/с$ под углом $alpha = 10^{ circ}$ к плоской поверхности горки, образующей угол $beta = 40^{ circ}$ с горизонтом. Пренебрегая сопротивлением воздуха, определить минимальный радиус кривизны траектории тела.
Решение:
Хорошо известно, что движение тела, брошенного под углом к горизонту вблизи поверхности земли, происходит по параболе. Радиус кривизны параболы уменьшается при приближении к ее вершине и минимален в ней. Однако, в данной задаче непосредственно невидно, где располагается вершина: наднаклонной плоскостью или подней. Выясним это.
Выберем систему отсчета XOY (см. рис.) и будем рассматривать движение точки, исходя из принципа независимости движения, как сумму двух прямолинейных движений. По оси ОХ движение равномерное ($a_{x} = 0$), а по оси OY-равнопеременное ($a_{y} = — g$).
Полное кинематическое описание рассматриваемого движения дает система уравнений
$x = v_{ox}t, y = v_{oy}t — frac{1}{2}gt^{2}$, (1)
$v_{x} = v_{ox}, v_{y} = v_{oy} — gt, v_{ox} = v_{0} cos ( alpha + beta), v_{oy} = v_{0} sin ( alpha + beta)$. (2)
Максимальную высоту подъема тела над поверхностью найдем из условия, что в наивысшей точке траектории $v_{y} = 0$, т.е.
$v_{y} = 0 = v_{0} sin ( alpha + beta ) — g t_{max}$.
Отсюда, время подъема тела на максимальную высоту
$t_{max} = frac{v_{0} sin ( alpha + beta) }{g}$.
Следовательно,
$h_{max} = y(t_{max}) = frac{v_{0}^{2} sin^{2} ( alpha + beta) }{g} — frac{g}{2} frac{ v_{0}^{2} sin^{2} ( alpha + beta) }{g^{2} } = frac{v_{0}^{2} sin^{2} ( alpha + beta) }{2g}$.
Координата $x_{верш}$, соответствующая максимальной высоте траектории, равна
$x_{верш} = x(t_{max}) = v_{0} sin ( alpha + beta ) t_{max} = frac{v_{0}^{2} sin ( alpha + beta) cos ( alpha + beta) }{g}$.
Тогда отношение
$frac{h_{max}}{x_{max}} = frac{v_{0}^{2} sin^{2} ( alpha + beta) }{2 v_{0}^{2} sin ( alpha + beta) cos ( alpha + beta) } = frac{1}{2} tg ( alpha + beta) = 0,6$
«задает направление» из точки броска в вершину траектории, которому соответствует угол $gamma = arctg 0,6 = 31^{ circ}$. Так как поверхность горки образует с горизонтом угол $beta = 40^{ circ}$, то это означает, что вершина траектории находится «в горке». Следовательно, радиус кривизны траектории минимален в точке падения тела на поверхность горки (в точке Р):
$R_{min} = frac{v_{p}^{2} }{a_{pn}}$,
где $v_{p}, a_{pn}$ — скорость и нормальное ускорение тела в точке Р соответственно:
$v_{p} = sqrt{v_{px}^{2} + v_{py}^{2}} = sqrt{ v_{n}^{2} cos^{2} ( alpha + beta) + [ v_{0} sin ( alpha + beta) — gt_{p} ]^{2}}$.
$a_{pn} = g cos phi = g frac{v_{px} }{v_{p} } = frac{v_{0} cos ( alpha + beta) }{ sqrt{ v_{0}^{2} cos^{2} ( alpha + beta ) + [ v_{0} sin ( alpha + beta) — gt_{p} ]^{2} } }$.
Следовательно,
$R_{min} = frac{( v_{0}^{2} cos^{2} ( alpha + beta) + (v_{0} sin ( alpha + beta ) — gt_{p} )^{2} )^{3/2}}{gv_{0} cos ( alpha + beta) }$.
Время $t_{p}$, соответствующее моменту падения тела на поверхность горки, найдем из уравнений (1)-(2):
$S cos beta = v_{0} cos ( alpha + beta) t_{p}, S sin beta = v_{0} sin ( alpha + beta ) t_{p} — frac{1}{2} gt_{p}^{2}$,
где $S$ — дальность полета тела, измеренная вдоль горки. Откуда получим:
$t_{p} = frac{2v_{0} cos ( alpha + beta) ( tg ( alpha + beta ) — tg beta ) }{g}$.
Следовательно,
$R_{min} = frac{ v_{0}^{2} (1 — 2 sin 2( alpha + beta)(tg ( alpha + beta) — tg beta) + 4 cos^{2} ( alpha + beta) (tg ( alpha + beta) — tg beta)^{2} )^{3/2} }{g cos ( alpha + beta) } = 5,8 м$.