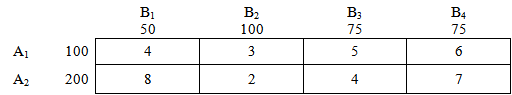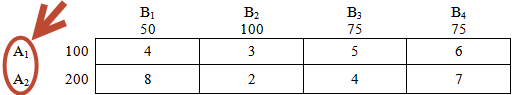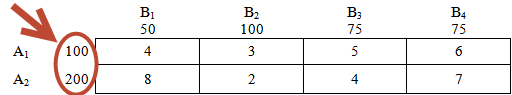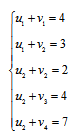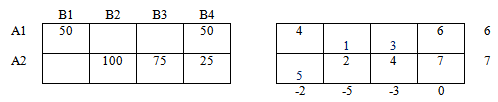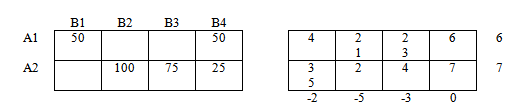Метод минимальной стоимости прост и позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи C=(cij).
Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости:
и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую , заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы груза использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.
Пример 38.2
Используя метод минимальной стоимости построить начальное опорное решение транспортной задачи.
Решение:
1. Запишем отдельно матрицу стоимостей для того, чтобы было удобнее выбирать минимальные стоимости.
2. Среди элементов матрицы стоимостей выбираем наименьшую стоимость C11=1, отмечаем ее кружочком. Данная стоимость имеет место при перевозке груза от 1-го поставщика 1-му потребителю. В соответствующую клетку записываем максимально возможный объем перевозки:
x11 = min {a1; b1} = min {60; 40} =40 т.е. минимум между запасами 1-го поставщика и запросами 1-го потребителя.
2.1. Запасы 1-го поставщика уменьшаем на 40.
2.2. Исключаем из рассмотрения 1-го потребителя, так как его запросы полностью удовлетворены. В матрице C вычеркиваем 1-ый столбец.
3. В оставшейся части матрицы C минимальной стоимостью является стоимость C14=2. Максимально возможная перевозка, которую можно осуществить от 1-го поставщика 4-му потребителю равна x14 = min {a1‘; b4} = min {20; 60} = 20, где a1 со штрихом это оставшиеся запасы первого поставщика.
3.1. Запасы 1-го поставщика исчерпаны, поэтому исключаем его из рассмотрения.
3.2. Запросы 4-го потребителя уменьшаем на 20.
4. В оставшейся части матрицы С минимальная стоимость C24=C32=3. Заполняем одну из двух клеток таблицы (2,4) или (3,2). Пусть в клетку запишем x24 = min {a2; b4} = min {80; 40} =40 .
4.1. Запросы 4-го потребителя удовлетворены. Исключаем его из рассмотрения вычеркивая 4-й столбец в матрице C.
4.2. Уменьшаем запасы 2-го поставщика 80-40=40.
5. В оставшейся части матрицы C минимальная стоимость C32=3. Запишем в клетку (3,2) таблицы перевозку x32 = min {a3; b2} = min {100; 60} =60.
5.1. Исключим из рассмотрения 2-го потребителя. Из матрицы C исключаем 2-ой столбец.
5.2. Уменьшим запасы 3-го поставщика 100-60=40
6. В оставшейся части матрицы C минимальная стоимость C33=6. Запишем в клетку (3,3) таблицы перевозку x33 = min {a3‘; b3} = min {40; 80} =40
6.1. Исключим из рассмотрения 3-го поставщика, а из матрицы C 3-ю строку.
6.2. Определяем оставшиеся запросы 3-го потребителя 80-40=40.
7. В матрице C остался единственный элемент C23=8. Записываем в клетку таблицы (2,3) перевозку X23=40.
8. Проверяем правильность построения опорного решения.
Число занятых клеток таблицы равно N=m+n — 1=3+4 -1.
Методом вычеркивания проверяем линейную независимость векторов-условий, соответствующих положительным координатам решения. Порядок вычеркивания показан на матрице X:
Вывод: Решение методом минимальной стоимости (таблица 38.3) является «вычеркиваемым» и, следовательно опорным.
На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения ТЗ в Эксель
- Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).
- Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.
- Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).
- Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).
- Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)
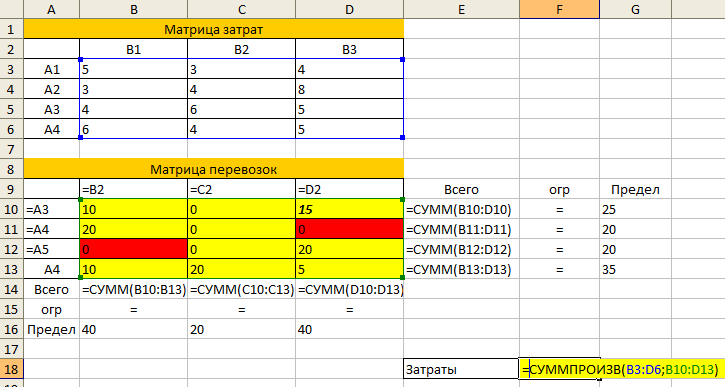
В режиме формул таблица будет выглядеть так:
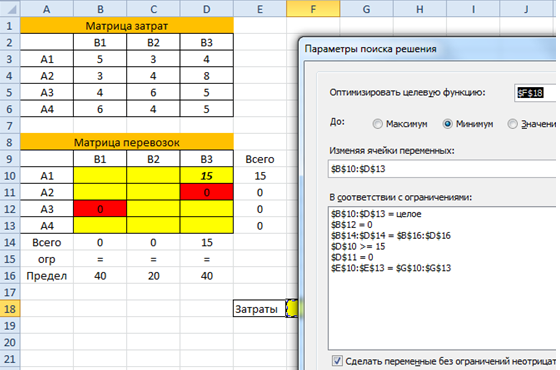
- Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).
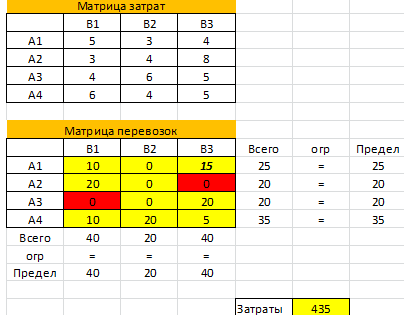
- Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).
- Проанализировать решение, если требуется и записать более подробно, например
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Спасибо за ваши закладки и рекомендации
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам
Решаем транспортные задачи любой сложности
Полезные ссылки
|
|
Метод минимальной стоимости
Идея
этого метода заключается в том, чтобы
заполнить клетки таблицы, начиная с
клетки с наименьшей стоимостью

Этот
метод, как правило, позволяет получить
более «выгодный» план, чем метод
«северо-западного угла».
Пример
19
Найти
начальный план перевозок методом
минимальной
стоимости, если
груз находится у трех поставщиков в
количествах 120, 85 и 135 единиц, который
необходимо доставить потребителям в
количествах 50, 90, 110 и 90 единиц, причем
стоимость транспортировки единицы
продукции от

поставщика в пункт потребления
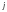
матрицей:
Решение
Решение
найдем методом минимальной стоимости:
|
Потребители
Поставщики |
50 |
90 |
110 |
90 |
|
120 |
5
|
11 70 |
10 |
8 |
|
85 |
10 |
8 20 |
4 |
2
|
|
135 |
9 |
7 |
1 110 |
5 25 |
Итак, начальный
план перевозок следующий

причем суммарная
стоимость затрат на перевозки равна:
Z(X)_=
1445
6.3 Метод потенциалов решения транспортной задачи
Общий
принцип определения оптимального плана
транспортной задачи методом потенциалов
аналогичен принципу решения задачи
линейного программирования
симплексным методом, а именно:
-
сначала
находят начальный опорный план
перевозок,
-
затем
переходят
к новому плану,
лучшему, такому, что
Z(
≤Z(
-
проверяют критерий
оптимальности
полученного решения:
Если
для некоторого опорного плана
транспортной
задачи существуют такие числа

что
,

то

оптимальный
план транспортной
задачи
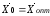
Числа
называются
потенциалами
соответственно
пунктов поставки и пунктов потребления.
Критерий
оптимальности
решения транспортной задачи следующий:
для
того чтобы
решение
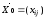
оптимальным, необходимо и
достаточно,
чтобы
существовала система
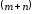

которые
удовлетворяли бы условиям:
для
всех базисных переменных (занятых
клеток) и
для
всех свободных переменных (пустых
клеток).
Алгоритм
метода
потенциалов решения транспортной
задачи
-
Найти
начальный план перевозок транспортной
задачи
методом
«северо-западного угла»
или методом минимальной стоимости.
Число
заполненных клеток должно быть равным
.
-
Найти
.
-
Найти
потенциалы
из
системы уравнений:
,
составленной для занятых клеток. -
Найти
оценки
для
свободных клеток:
.
-
Если
среди чисел
нет
отрицательных
значений, все,
то найденный опорный планявляется
оптимальным. -
Если
же для некоторой свободной клетки
,
то исходный опорный план не
является оптимальным и необходимо
перейти к новому опорному плану
,
причем
Z(
≤Z(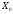
-
Чтобы
решение
улучшить, выбирают среди отрицательных
оценок
наибольшую по абсолютной величине (при
нескольких равных выбирают
любую) и для соответствующей свободной
клетки строим
цикл
пересчета.
Цикл
–
это замкнутая ломаная, соединяющая
несколько занятых клеток таблицы. Две
последовательные вершины цикла лежат
либо в одной строке, либо в одном столбце;
в одной их них объем увеличивается (в
клетке
ставится знак «+»); в другой – уменьшается
настолько же единиц
(в клетке ставится знак «–»).
7. Среди
клеток, имеющих знак «–» отыскивается
та, которая содержит минимальную
величину поставки. Эта величина
прибавляется к содержимому
клеток, имеющих знак «+» и вычитается
из содержимого клеток,
имеющих знак «–».
8. Для
нового опорного плана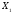
рассчитываются потенциалы

оценки(п.3)
Замечание
Потенциалам

можно
придать простой экономический смысл:

стоимость единицы
груза для

поставщика,
– стоимость
единицы груза у

потребителя.
Если
для некоторой свободной
клетки величина
т.е.
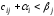
Это
означает,
что перевозки из пункта
в
пункт
приведут к уменьшению стоимости единицы
груза в пункте назначения, а переменную

внести в базис. В то же время равенство
для базисных переменных (занятых клеток)
означает, что
перевозки, внесенные в план, должны быть
«безубыточными», а стоимость груза
в пункте отправления плюс издержки
на
перевозку должны в точности
покрываться стоимостью груза в
пункте
потребления.
Пример
20
Найти
оптимальный план перевозок, при котором
суммарная стоимость всех перевозок –
наименьшая,
если
груз находится у трех поставщиков в
количествах 12
, 8 и 10 единиц, который необходимо
доставить потребителям в количествах
6, 9 , 15
единиц, причем
стоимость транспортировки единицы
продукции от

поставщика в пункт потребления

матрицей:
Решение
Составим
математическую модель задачи.
Обозначим:

единиц груза перевозимого от i-ого
поставщика отправления к j-у
потребителю
Условия
задачи запишем в таблицу
|
Потребители
Поставщики |
6 |
9 |
15 |
|
12 |
1 |
3 |
4 |
|
8 |
2 |
5 |
3 |
|
10 |
6 |
7 |
5 |
Так
как

то транспортная задача – закрытая. На
искомые
перевозки xij
по
смыслу задачи необходимо наложить
следующие условия:
а)
условия по запасам:
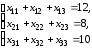
б)
условия по потребностям:

в)
условия неотрицательности:
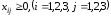
Транспортные
расходы при таком плане перевозок
составят:

Начальный
план перевозок найдем методом
северо-западного угла:
|
Потребители
Поставщики |
6 |
9 |
15 |
|
12 |
1
|
3 6 |
4 |
|
8 |
2 |
5 3 |
3 5 |
|
10 |
6 |
7 |
5 10 |
В
результате получаем начальный
опорный
план
Переменные,
стоящие в занятых клетках таблиц,
являются
базисными,
а
остальные ( в пустых клетках) –
свободными.
Полученный
план перевозок является допустимым,
т.к.
удовлетворяет ограничениям
задачи. Это выражается в том, что сумма
объемов перевозок в каждом
столбце равна потребностям; а в строке
запасам.
Согласно
данному плану перевозок, общая стоимость
перевозок всего груза составляет:

Найдем
потенциалы
из
системы уравнений:

составленной для занятых клеток,
очевидно, что

Поскольку
количество неизвестных шесть и
на
единицу превышает число уравнений
в системе (пять занятых клеток), то одно
из неизвестных (обычно) принимаем за
нуль,
например,
a1=0,
тогда потенциалы остальных строк и
столбцов однозначно определяются:

Запишем
их в таблице:
|
Потребители
Поставщики |
6 |
9 |
15 |
|
|
12 |
1
|
3 6 |
4 |
|
|
8 |
|
5 3 |
3 5 |
|
|
10 |
6 |
7 |
5 10 |
|
|
|
|
|
Найдем
оценки
из системы уравнений:

Оценка
отрицательная,
следовательно, решение

является оптимальным,
а значение целевой функции

104 можно уменьшить.
Построим
цикл.
Так как оценка
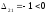
то переменную x21
введем
в базис (клетку (2,1)
сделаем
занятой). В эту клетку запишем число
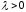
Сумма перевозок по строкам и столбцам
таблицы должна оставаться неизменной,
необходимо восстановить баланс каждой
строки и столбца. Будем прибавлять
или вычитать

клетках.Для
свободной клетки (2,1)
можно построить единственный цикл
пересчета: (2,1),
(1,1), (1,2), (2,2),(2,1)
Если
соединить последовательно клетки цикла
отрезками прямой,
то получится замкнутая ломаная линия,
каждый отрезок которой лежит
либо в строке, либо в столбце, и только
одна из вершин этой ломаной лежит
в свободной клетке, т.е. в клетке (2,1),
Запишем
в клетку (2,1),)
число
и
поставим знак «+», в соседних с ней
вершинах цикла поставим знак «-»,
|
Потребители
Поставщики |
6 |
9 |
15 |
|
12 |
 
6 |

6 |
4 |
|
8 |
|
5 3 — |
3 5 |
|
10 |
6 |
7 |
5 10 |
Число
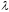
из чисел, находящихся в «отрицательных»
клетках:

Свободная
клетка (2,1)
стала
занятой.
Итак,
перешли к новому опорному решению
|
Потребители
Поставщики |
6 |
9 |
15 |
|
12 |
1
|
3 9 |
4 |
|
8 |
|
5 |
3 5 |
|
10 |
6 |
7 |
5 10 |
Затраты
на перевозки по плану

Проверим
решение

метода потенциалов.
Найдем
потенциалы

системы:
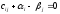
составленной
для занятых клеток, очевидно, что
Запишем
в таблице найденные потенциалы
|
Потребители
Поставщики |
6 |
9 |
15 |
|
|
12 |
1
|
3 9 |
4 |
|
|
8 |
3 |
5 |
3 5 |
|
|
10 |
6 |
7 |
5 10 |
|
|
|
|
|
Вычислим
оценки

Все
оценки

Следовательно, решение
При
этом затраты на перевозку будут
минимальными:

Дадим
экономическое истолкование оптимального
решения данной задачи:
для
того, чтобы затраты на перевозку груза
от потребителей
к
поставщикам
были
наименьшими и равными 101 ед. стоимости,
необходимо отправить
-
от
первого поставщика 3 ед. груза и 9 ед.
груза
соответственно
первому и второму потребителю;
-
от
второго поставщика 3 ед. груза и 5 ед.
груза
соответственно
первому и третьему потребителю;
-
от
третьего поставщика 10 ед. груза
третьему
потребителю.
Транспортная задача. Методы решения
Транспортная задача, это специальный вид задачи линейного программирования. Для решения транспортной задачи можно использовать методы решения задач линейного программирования, однако ввиду специфического вида задачи, были построены алгоритмы специально для решения этой задачи. Для решения транспортной задачи в онлайн режиме с подробными пояснениями пользуйтесь калькулятором транспортная задача онлайн.
- Содержание
- 1. Математическая постановка транспортной задачи
- 2. Определение опорного плана. Предварительные сведения
- 3. Метод северно-западного угла
- 4. Метод минимального элемента
- 5. Метод аппроксимации Фогеля
- 6. Метод потенциалов
- 7. Метод дифференциальных рент
1. Математическая постановка транспортной задачи.
Общая постановка транспортной задачи заключается в определении оптимального плана перевозок некоторого однородного груза из пунктов отправления A1, A2,…, Am в пункты назначения B1, B2,…, Bn. Критерий оптимальности берется минимальная стоимость перевозки или минимальное время доставки груза.
Рассмотрим транспортную задачу, где в качестве критерия оптимальности взята минимальная стоимость перевозок всего груза. Обозначим через Сij тарифы перевозки единицы груза из пункта отправления i в пункт назначения j. Обозначим через Ai запасы груза i-м пункте отправления, а через Bj потребности груза j-м пункте назначения, а через Xj количество единиц груза переводимого из пункта отправления i в пункт назначения j.
Тогда математическая модель транспортной задачи состоит в определении минимального значения функции
 |
(1.1) |
при условиях
 |
(1.2) |
 |
(1.3) |
 |
(1.4) |
Поскольку удовлетворяется условия (1.2)−(1.4), то обеспечивается доставка необходимого количества груза в каждый из пунктов назначения, вывоз груза из всех пунктов отправления, а также исключаются обратные перевозки.
Определение 1. Любое неотрицательное решение Xij=∥xij∥ (i=1,..,m; j=1,…,n) систем (1.2) и (1.3) называется допустимым планом транспортной задачи.
Определение 2. План 
Если сумма груза у поставщиков равно общей сумме потребностей в пунктах назначения:
 |
(1.5) |
то модель транспортной задачи называется закрытой (или сбалансированной). Если (1.5) не удовлетворяется, то модель транспортной задачи называется открытой (или несбалансированной).
Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие (1.5).
В случае превышения запаса над потребностью, т.е. при
 , , |
вводится фиктивный (n+1)-ый пункт назначения с потребностью
 . . |
Соответствующие тарифы считаются равными нулю: ci n+1=0 (i=1,…,m). После этих преобразований получим закрытую модель транспортной задачи.
Аналогично, при 

Мы будем рассматривать закрытую модель транспортной задачи. Если же модель транспортной задачи является открытой, то с помощью вышеизложенных преобразований строим закрытую модель транспортной задачи.
Обычно данные транспортной задачи записывают в виде таблицы:
Число переменных Xij равно mn, где m число пунктов отправнения , а n число пунктов назначения. Число уравнений в (1.2) и (1.3) равно m+n. Так как мы рассматриваем закрытую модель транспортной задачи (выполняется равенство (1.5)), то число линейно независимых уравнений равно m+n−1. Следовательно опорный план транспортной задачи может иметь не более m+n−1 отличных от нуля неизвестных.
Если в опорном плане количество отличных от нуля компонентов равно в точности m+n−1, то опорный план называется невырожденным, а если меньше − то вырожденным.
Для решения транспортной задачи сначала определяется начальный опорный план, а затем определяется оптимальный план путем улучшения текущего опорного плана.
Для определения начального опорного плана существует несколько методов. Мы рассмоьтрим три метода. Метод северно-западного угла, метод минимального элемента и метод аппроксимации Фогеля.
2. Определение опорного плана. Предварительные сведения
Опорный план транспортной задачи находим следующим образом. На каждом шаге в таблице условий задачи заполняем одну клетку, которая называется занятой. Обозначим через Kij клетку, где i -номер пункта отправления (строка), j-номер пункта назначения (столбец). Клетку Kij заполняем так, чтобы удовлетворялись полностью потребности пункта назначения j, либо обеспечивался полный вывоз груза из пункта отправления i.
В первом случае временно исключаем из рассмотрения столбец j и изменяем запас груза пункта отправления i. Во втором случае временно исключаем из рассматрения строку i и изменяем потребность груза пункта назначения j. Далее повторяем процедуру с таблицей условий с исключенной строкой или столбцом.
В m+n−1-ом шаге получаем задачу с одним пунктом отправления и одним пунктом назначения. Остается свободной одна клетка. Запасы оставшегося пункта отправления будут равны потребностям пункта назначения. Заполнив эту клетку заканчиваем m+n−1-ый шаг и получаем опорный план.
Если на некотором шаге (но не на последнем) потребности очередного пункта назначения равны запасам пункта отправления, то временно исключаем из рассмотрения либо столбец, либо строку (только одно из двух). Тогда либо запасы данного пункта отправления, либо потребности данного пункта назначения считаем равным нулю. Этот нуль при очередном шаге записываем в очередную заполняемую клетку. Данный подход обеспечивает ровно m+n−1 занятых клеток, что обеспечивает возможность проверки полученного опорного плана на оптимальность и нахождение оптимального плана.
Для нахождения опорного плана транспортной задачи в онлайн режиме тремия методами с подробными пояснениями пользуйтесь калькулятором транспортная задача онлайн.
3. Метод северно-западного угла
При нахождении опорного плана транспортной задачи методом северно-западного угла, заполнене клеток таблицы условий начинают с верхней левой клетки K11 поэтому метод и называется «метод северно западного угла»).
Рассмотрим метод на конкретном примере.
Пример 1. На три базы A1, A2, A3 поступил очередной груз в количествах равных 140, 160, 120 ед. Этот груз требуется перевезти в четыре пунктов назначения B1, B2, B3, B4 в количествах 150, 90, 100, 80. Тарифы перевозок представлена матрицей
 . . |
Найти план перевозок даной транспортной задачи методом северно-западного угла.
Решение. Запишем все данные в таблицу условий:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы.
Наличие груза у поставщиков равно: ∑Ai=140+160+120=420.
Общая потребность в грузе в пунктах назначения равна: ∑Bj=150+90+100+80=420.
∑Ai=∑Bj. Модель транспортной задачи является закрытой. Следовательно она разрешима.
Найдем опорный план задачи методом северно-западного угла.
A1≤B1. Следовательно в клетку (A1, B1 ) помещаем число min(A1, B1)=140. Запасы пункта A1 полностью исчерпаны. Поэтому исключаем из рассмотрения строку A1 и будем считать потребности пункта B1 равными 150−140=10.
A2>B1. Следовательно в клетку (A2, B1) помещаем число min(A2, B1)=10. Потребности пункта B1 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B1 и будем считать запасы пункта A2 равными 160−10=150.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
F=2·140+8·10+4·90+ 1·60+3·40+6·80=1380.
4. Метод минимального элемента
В отличие от метода северно-западного угла, в методе минимального элемента выбор пунктов отправления и пунктов назначения производится ориентируясь на тарифы перевозок, т.е. в каждом шаге нужно выбрать клетку с минимальным тарифом перевозок. Если таких клеток несколько, то выбираем один из них. Надо отметить, что при данном методе определения заполняемой клетки, стоимость перевозок как правило бывает меньше, чем при методе северно западного угла. Поэтому целесообразно начальный опорный план найти методом минимального элемента.
Рассмотрим метод минимального элемента на примере.
Пример 2. Найти опорный план транспортной задачи представленной в таблице условий ниже методом минимального элемента:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из кажного пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно: 
Общая потребность в грузе в пунктах назначения равна: 

Минимальный тариф равный 1 находится в клетке (A1, B3). Поэтому заполняем эту клетку.
A1>B3. Следовательно в клетку (A1, B3) помещаем число 70. Потребности пункта B3 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B3 и будем считать запасы пункта A1 равными 150−70=80.
Минимальный тариф равный 1 находится в клетке (A2, B4). Поэтому заполняем эту клетку.
A2>B4. Следовательно в клетку (A2, B4) помещаем число 40. Потребности пункта B4 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B4 и будем считать запасы пункта A2 равными 100−40=60.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
5. Метод аппроксимации Фогеля
Суть метода аппроксимации Фогеля заключается в следующем. Для каждой строки и для каждого столбца находим разности между двумя записанными в них минимальными тарифами. Полученные разности записываем в специально отведенные для этого столбце и в строке в таблице условий задачи.
Среди указанных разностей выбираем максимальную. В строке (или в столбце), которой данная разность соответствует, определяем минимальный тариф. Клетку, в которой он записан заполняем на данной итерации.
Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбираем ту клетку, которая соответствует наибольшей разности между двумя минимальными тарифами в данном столбце (строке).
Применение метода аппроксимации фогеля позволяет получить либо опорный план, близкий к оптимальнму, либо сам оптимальный план.
Рассмотрим метод аппроксимации Фогеля на примере 2, рассмотренной выше.
Пример 3. Найти опорный план транспортной задачи представленной в таблице условий ниже методом аппроксимации Фогеля:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из кажного пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно: 
Общая потребность в грузе в пунктах назначения равна: 

Для каждой строки Ai найдем разности между двумя минимальными тарифами, записанными в данной строке и поместим их в соответствующем дополнительном столбце.
В строке 1 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1. В строке 2 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В строке 3 минимальный тариф равен 3, а следующий за ним равен 3, разность между ними 3−3=0.
Для каждого столбца Bj найдем разности между двумя минимальными тарифами, записанными в данном столбце и поместим их в соответствующей дополнительной строке.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 3 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1.
Вычислив все разности выберем наибольшую из них. В данном случае наибольшая разница равна 2. В этом столбце минимальный тариф равен 1 и находится в пересечении строки A 1 и столбца B3. Следовательно заполняем эту клетку.
A1>B3. Следовательно в клетку помещаем число 70. Потребности пункта B3 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B3 и будем считать запасы пункта A1 равными 150−70=80.
Для каждой строки Ai найдем разности между двумя минимальными тарифами, записанными в данной строке и поместим их в соответствующем дополнительном столбце.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 3 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1. В строке 1 минимальный тариф равен 2, а следующий за ним равен 2, разность между ними 2−2=0. В строке 2 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В строке 3 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1.
Для каждого столбца Bj найдем разности между двумя минимальными тарифами, записанными в данном столбце и поместим их в соответствующей дополнительной строке.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1.
Вычислив все разности выберем наибольшую из них. В данном случае наибольшая разница равна 2. В этой строке минимальный тариф равен 1 и находится в пересечении строки A2 и столбца B4. Следовательно заполняем эту клетку.
A2>B4. Следовательно в клетку помещаем число 40. Потребности пункта B4 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B4 и будем считать запасы пункта A2 равными 100−40=60.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
F=2·40+3·40+1·70+ 4·60+1·40+3·100=850.
Для определения оптимального плана транспортной задачи разработано нескольно методов. Мы расмотрим метод потенциалов и метод дифференциальных рент.
6. Метод потенциалов
Процедура нахождения оптимального плана транспортной задачи имеет два этапа. На первом этапе находят опорной план транспортной задачи. Далее последовательно улучшают найденный опорный план до получения оптимального плана.
Для определения опорного плана будем пользоваться методом северно-западного угла, методом минимального элемента или методом аппроксимации Фогеля рассмотренных выше.
Для онлайн решения задачи методом потенциалов пользуйтель калькулятором транспортная задача онлайн.
При применении этих методов получаем m+n−1 занятых клеток в исходном плане. Отметим, что в некоторых клетках могут стоять нули. Полученный план следует проверить на оптимальность.
Теорема. Если для некоторого опорного плана 
для всех i=1,..,m; j=1,…,n, то 
Определение 6.1. Числа αi и βj (i=1,..,m; j=1,…,n) называются потенциалами пунктов отправления и пунктов назначения, соответственно.
Вышеизложенная теорема позволяет построить алгоритм нахождения оптимального плана транспортной задачи.
Алгоритм состоит в следующем. Предположим, что одним из рассмотренных выше методов найден опорный план транспортной задачи. Для каждого из пунктов отправления и назначения определяют потенциалы αi и βj (i=1,..,m; j=1,…,n) из системы уравнений
где сij − тарифы транспортной задачи в заполненных клетках.
Так как число заполненных клеток равно m+n−1, то система (6.1) с m+n неизвестными содержит m+n−1 уравнений. Для решения данной задачи одно из неизвестных можно сделать равным нулю и найти остальные неизвестные. После этого, для свободных клеток определяем числа
Если среди чисел αij нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки αij>0, то данный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых αij>0 и среди данных чисел выбирают максимальное. Клетку с данным числом следует заполнить.
Надо учитывать, что при заполнении данной клетки необходимо изменить объем поставок в нескольких других клетках.
Определение 6.2. Циклом в таблице условий транспортной задачи называется ломанная линия, вершины которой расположены в занятых клетках таблицы, а звеня расположены вдоль строк и столбцов. В каждой вершине цикла встречается два звена, одно из которых находится в строке, а другой в столбце.
Если ломаннная линия, образующая цикл, самопересекается, то место пересечения не является вершиной. Некоторые циклы представлены на рисунке Рис.6.1.
При правильном строении опорного плана для любой свободной клетки можно построить только один цикл. После построения цикла следует перейти к новому опорному плану. Для этого в каждой из клеток, находящихся на вершине цикла записывают определенный знак «+» или «−» . В свободной клетке записывают знак «+» и поочередно проходя по циклу записывают знаки «−» и «+». Назовем клетки с записанными в них знаками плюсовыми и минусовыми.
Далее в свободную клетку переносят меньшее из чисел xij, находящихся в минусовых клетках. Это число прибавляют к числам, стоящим в плюсовых клетках а вычисляют из чисел, стоящих в минусовых клетках. Клетка, которая была свободной, становится занятой, а минусовая клетка с минимальным из чисел xij, находящихся в минусовых клетках считается свободным.
В результате вышеуказанных перемещений груза по циклу, получим новый опорный план транспортной задачи. Описанный переход от одного опорного плана транспортной задачи к другому опорному плану называется сдвигом по циклу пересчета.
При сдвиге по циклу пересчета число занятых клеток не изменяется и равно m+n−1. Если в минусовых клетках имеется два и более одинаковых минимальных числа xij, то освобождают только одину, о остальные оставляют занятыми с нулевыми значениями.
Далее полученный опорный план проверяют на оптимальность. Для этого определяют потенциалы пунктов отправления и назначения и находят числа αij=βj−αi−cij для всех свободных клеток. Если среди них не окажется положительный, то получен оптимальный план. Если же среди них есть положительный, то нужно перейти к новому опорному плану. После конечнего числа шагов получяют оптимальный план.
Таким образом алгоритм нахождения оптимального плана содержит следующие этапы:
1. Нахождение опорного плана. При этом число заполненных клеток должно быть равным m+n−1.
2. Нахождение потенциалов αi и βj (i=1,..,m; j=1,…,n) пунктов отправления и назначения соответственно.
3. Определение числа αij для каждой свободной клетки. Если среди αij нет положительных, то получен оптимальный план транспортной задачи. Если же они имеются, то делается переход к новому опорному плану.
4. Выбор максимального среди положительных чисел αij . Определение свободной клетки, которую нужно заполнить. Построение цикла пересчета для выбранной свободной клетки. Сдвиг по циклу пересчета.
5. Проверка полученного опорного плана на оптимальность, т.е. переход к пункту 2.
Отметим, что в некотором шаге опорный план может стать вырожденным. Чтобы избежать зацикливания следует преобразовать вырожденный план в невыроженный путем замены соответствующий нулевых элементов опорного плана на сколь угодно малыми положительными числами δ и решить задачу. После решения, в оптимальном плане нужно заменить δ нулем.
Рассмотрим метод потенциалов на примере.
Пример 6.1. Решить транспортную задачу, заданную в таблице условий методом потенциалов:
Решение. Найдем сначала опорный план с помощью одного из методов описанного выше. Пусть это будет метод минимального элемента. Тогда после m+n−1 шагов получим следующую таблицу с опорным планом:
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=2, β3=1, α2=-1, α3=-3, β4=0, β2=5
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α12=2, α14=-2, α22=2, α23=-3, α33=-1, α34=-3.
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки A1 и столбца B2. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак «+» а остальные клетки цикла поочередно знаки «−» и «+».
Наименьшее из чисел в минусовых клетках равно 80. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках добавляется 80, а из чисел, находящихся в минусовых клентках вычитается это число.
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=3, β3=1, α3=-3, β1=0, α2=-3, β4=-2
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α11=-2, α14=-4, α22=2, α23=-1, α33=1, α34=-3.
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки A2 и столбца B2. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак «+» а остальные клетки цикла поочередно знаки «−» и «+».
Наименьшее из чисел в минусовых клетках равно 20. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках добавляется 20, а из чисел, находящихся в минусовых клентках вычитается это число.
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=3, β3=1, α2=-1, β1=2, β4=0, α3=-1
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α11=0, α14=-2, α23=-3, α32=-2, α33=-1, α34=-3.
Среди чисел αij нет положительных. Следовательно данный опорный план является оптимальным.
Ответ. Оптимальный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
7. Метод дифференциальных рент
При нахождении решения транспортной задачи методом дифференциальных рент сначала распределяем часть груза наилучшим образом между пунктами назначения и получаем так называемое условно оптимальное распеделение. На последующих итерациях уменьшаем общий объем нераспределенных поставок. Для решения транспортной задачи методом дифференциальных рент в онлайн режиме с подробными пояснениями пользуйтесь калькулятором метод дифференциальных рент онлайн.
Начальное распределение груза определяется следующим образом. Для каждого столбца определяем минимальный тариф и заключаем в квадрат. Клетки с тарифами в квадратах заполняем максимально возможными числами. В результате получим некоторое распределение поставок груза в пункты назначения. Это распределение в общем случае не удовлетворяет ограничениям транспортной задачи. Далее шаг за шагом нужно постепенно сокращать нераспределенные поставки груза так, чтобы общая стоимисть перевозки оставалась минимальным. Для этого определяем избыточные и недостаточные строки.
Определение 7.1. Строки, соответствующие пунктом отправления, запасы которых полностью распределены а среди пунктов назначения, связанные с этим распределением есть неудовлетворенные потребности называются недостаточными или отрицательными.
Определение 7.2. Строки, запасы которых не распределены полностью называются избыточными или положительными.
После определения недостаточных и избыточных строк, в дополнительном столбце записываем величину избытка или недостатка. Избыток записывается со знаком «+», а недостаток со знаком «-«.
В случае избытка для данной строки в дополнительном столбце записываем разность между запасом груза данного пункта отправления и суммой всех поставок данной строки. Если же данная строка недостаточная, то определяем общий объем поставок, которая недостает для удовлетворения всех потребностей пунктов назначения, связанных с данным распределением груза.
После определения избыточных и недостаточных строк, для каждого столбца находим разности между числом в квадрате и ближащим к нему тарифом, записанным в избыточной строке. Если число в квадрате стоит в избыточной строке, то разность не определяем. Все разности записываем в дополнительной строке. Среди этих разностей находим наимельшее. Это число называется промежуточной рентой. Далее переходим к новой таблице. Эта таблица получается из предыдущей таблицы прибавлением промежуточной ренты к соответствующим тарифам, стоящим в недостаточных строках. Остальные элементы оставляем прежними. Все клетки новой таблицы считем свободными и начинаем их заполнять. В новой таблице число заполненных клеток на одну больше, чем в предыдущей таблице. Эта клетка находится в столбце с промежуточной рентой.
Так как число заполненных клеток больше, чем столбцов, то при заполнении следует соблюдать специальное правило, которое состоит в следующем.
Выбираем некоторый столбец (строку), в котором имеется одна клетка с помещенным в ней квадратом. Эту клетку заполняем и исключаем из рассмотрения данный столбец (строку). После этого берем некоторую строку (столбец), в котором имеется одна клетка с помещенным в ней квадратом. Эту клетку заполняем и исключаем из рассмотрения данную строку (столбец). Продолжая так, после конечного числа шагов заполняем все клетки, в которых помещены квадраты с записанными в них числами.
Если удается распределить весь груз в пунктах отправления между пунктами назначения, то получаем оптимальный план. В противном случае переходим к новой таблице. Для этого находим извыточные и недостаточные строки, прмежуточную ренту и на основе этого строим новую таблицу.
При определении избыточности или недостаточности строк могут возникнуть трудности когда ее нераспределенный остаток равен нулю. Этот вопрос мы рассмотрим ниже на конкретном примере.
После конечного числа итераций распределенный остаток станет равным нулю. В результате получим оптимальный план данной транспортной задачи.
Пример. Найти решение транспортной задачи представленной в таблице условий методом дифференциальных рент:
Решение. Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из каждого пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно:
Общая потребность в грузе в пунктах назначения равна:

Найдем оптимальный план транспортной задачи методом дифференциальных рент.
Итерация 1:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Если в каком-либо столбце окажется несколько одинаковых минимальных тарифов, то выбираем какой-нибудь из них, причем неважно какой. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A1B1, A3B2, A2B3, A2B4.
В результате заполнения отмеченных клеток получен условно оптимальный план.
После получения условно оптимального плана определяем избыточные и недостаточные строки. Строка A1 является недостаточной, поскольку запасы пункта отправления A1 распределены полностью, а потребности пункта назначения B1 удовлетворены частично. При этом величина недостатка равна 20. Строка A3 является недостаточной, поскольку запасы пункта отправления A3 распределены полностью, а потребности пункта назначения B2 удовлетворены частично. При этом величина недостатка равна 20. Строка A2 является избыточным, поскольку запасы пункта отправления A2 распределены не полностью. При этом величина избытка этой строки равна 40.
Нераспределенный остаток равен 40. Суммарный объем поставок равен 150.
После определения избыточных и недостаточных строк, по каждому из столбцов находим разности между минимальными тарифами, записанными в избыточных строках, и тарифами, стоящими в заполненных клетках.
В столбце 1 минимальный тариф в избыточных строках равно 4 а число стоящее в рамке равно 2. Cледовательно, разность для данного столбца равна 4−2=2. В столбце 2 минимальный тариф в избыточных строках равно 3 а число стоящее в рамке равно 2. Cледовательно, разность для данного столбца равна 3−2=1. Для столбца 3 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 4 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке.
Избыточные и недостаточные оценки помещаем в дополнительный столбец, а разности в дополнительную строку:
Выбираем наименьшую из найденных разностей, которая является промежуточной рентой. В данном случае промежуточная рента равна 1 и находится в столбце B2. Далее переходим к следующей таблице. В этой таблице в строках (являющихся избыточными) переписываем соответствующие тарифы из предыдущей таблицы, а тарифы недостаточных строках получаются в результате прибавления к ним величину промежуточной ренты, т.е. 1.
Итерация 2:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A1B1, A2B3, A2B4, A2B2, A3B2.
В результате заполнения отмеченных клеток получен условно оптимальный план.
После получения условно оптимального плана определяем избыточные и недостаточные строки. Строка A1 является недостаточной, поскольку запасы пункта отправления A1 распределены полностью, а потребности пункта назначения B1 удовлетворены частично. При этом величина недостатка равна 20. Строка A3 является избыточным, поскольку запасы пункта отправления A3 распределены не полностью. При этом величина избытка этой строки равна 20.
Нераспределенный остаток равен 20. Суммарный объем поставок равен 170.
Избыточные и недостаточные оценки помещаем в дополнительный столбец.
Определяем положительность или отрицательность нулевой строки A2. Для этого запасы этой строки увеличиваем на 1 и снова заполняем таблицу. Если суммарный объем поставок не изменится, то строка положительная, в противном случае − отрицательная.
Последовательность заполнения клеток следующее: A1B1, A2B3, A2B4,A2B2, A3B2:
Суммарный объем поставок не изменился (170). Следовательно строка A2 избыточна (положительна).
После определения избыточных и недостаточных строк, по каждому из столбцов находим разности между минимальными тарифами, записанными в избыточных строках, и тарифами, стоящими в заполненных клетках.
В столбце 1 минимальный тариф в избыточных строках равно 4 а число стоящее в рамке равно 3. Cледовательно, разность для данного столбца равна 4−3=1. Для столбца 2 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 3 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 4 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке.
Выбираем наименьшую из найденных разностей, которая является промежуточной рентой. В данном случае промежуточная рента равна 1 и находится в столбце B1. Далее переходим к следующей таблице. В этой таблице в строках (являющихся избыточными) переписываем соответствующие тарифы из предыдущей таблицы, а тарифы недостаточных строках получаются в результате прибавления к ним величину промежуточной ренты, т.е. 1.
Итерация 3:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A2B3, A2B4, A1B1, A2B1, A3B1,A2B2, A3B2.
В результате заполнения отмеченных клеток получен условно оптимальный план. После получения условно оптимального плана определяем избыточные и недостаточные строки.
Посмотрев на таблицу выше мы видим, что избыточных и недостаточных строк нет. Нераспределенный остаток равен 0. Суммарный объем поставок равен 190. Все имеющие запасы распределены в соответствии фактическими потребностями пунктов назначения. Следовательно получен оптимальный план.
Ответ.
Оптимальный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
 |
В данной статье разберемся с решением транспортной задачи. Все действия будем выполнять пошагово с очень подробными пояснениями. Дадим определение, аналогичное тому, которое дано в ваших учебниках или лекциях. Определение:Транспортная задача — это математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов с минимизацией затрат на перемещение. |
Чтобы не загромождать страницу большим объемом пояснений, разобью весь материал на несколько частей — блоков.
Ну, начнем! Далее Вводная часть, с которой желательно ознакомиться.
Вводная часть, с которой желательно ознакомиться
Существует несколько методов решения транспортной задачи. Мы будем подробно рассматривать два из них:
- решение транспортной задачи методом потенциалов (рассмотрен в данной статье)
- решение транспортной задачи с использованием симплекс метода.
Решение задачи методом потенциалов происходит в несколько этапов:
- Определение опорного решения.
- Применение к найденному опорному решению самого метода потенциалов.
- Проверка единственности решения.
Определение опорного плана, в свою очередь, можно выполнить несколькими способами. Мы рассмотрим два из них:
- метод северо-западного угла
- метод минимальных стоимостей
(не путать с методами решения самой транспортной задачи!!!)
О чем говорится в определении транспортной задачи?
У нас есть некоторый груз, который находится на складах: склад 1, склад 2, …, склад — это пункты отправления.
Этот груз нам необходимо развести по магазинам: магазин 1, магазин 2, …, магазин k — это пункты назначения.
Нам выгоднее как можно эффективнее выполнить работу, т.е. найти такой вариант перевозки, при котором затраты будут минимальными.
Рассмотрим пример решения транспортной задачи подробно.
Транспортная задача задается следующей таблицей:
Далее, что означают числа в условии транспортной задачи?
Что означают числа в условии транспортной задачи?
Рассмотрим постановку транспортной задачи, т.е. что дано в условии и переведем ее с математического языка на язык, понятный нам.
Это наши «склады» — пункты отправления: два склада с товаром: А1 и А2
Это объем товара — количество груза, соответственно на складах А1 и А2:
Далее имеем дело с пунктами назначения — с «магазинами». В нашем случае их 4 штуки: В1, В2, В3 и В4.
И соответственно потребности каждого из магазинов — потребности пунктов назначения:

Числа внутри таблицы — матрица стоимостей, или по другому, расценки перевозки 1 единицы груза из соответствующих пунктов. Эти значения также могут интерпритироваться как расстояния между соответствующими пунктами. Подробности — в условии решаемой задачи.

Например, для перевозки 1 единицы груза из пункта отправления («склада») А2 в пункт назначения («магазин») В3 надо заплатить 4 условные единицы стоимости, например 4 руб.

Аналогично, мы заплатим 6 рублей за перевозку 1 единицы груза из «склада» А1 в «магазин» В4.

Или та же самая задача может быть задана сразу в более понятном виде:

Возможна текстовая постановка задачи. В этом случае необходимо самим заполнять все ячейки таблицы, исходя из заданных в условии значений.
Далее — Методы определения первоначального плана транспортной задачи.
Методы определения первоначального плана транспортной задачи.
Рассмотрим самый распространенный метод получения опорного плана — метод северо-западного угла.
Называется он так потому, что заполнение таблицы начинается с самой верхней левой (северо-западной) ячейки.
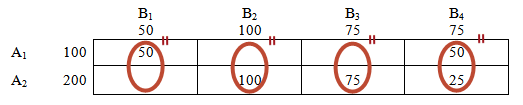
Перед тем, как распределять ресурсы по «магазинам», проверим, равны ли общие потребности имеющимся ресурсам?
Потребности: 50 + 100 + 75 + 75 = 300
Ресурсы: 100 + 200 = 300
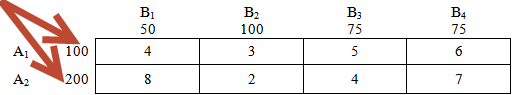
Потребности = Ресурсам
В этом случае говорят, что транспортная задача закрытая. Решение открытой транспортной задачи рассмотрим чуть позже.
Начнем нахождение опорного решения:
Заполним клетку (1;1).
В магазин В1 требуется 50 единиц товара. Со склада А1 отправим в этот магазин 50 единиц.
Потребности магазина В1 выполнены, следовательно, нет необходимости везти туда груз со склада А2.
На складе А1 еще осталось 50 единиц груза. Эти остатки можем направить в магазин В2. Ресурсы склада А1 исчерпаны.
Переходим к складу А2.
Так как потребности магазина В1 выполнены полностью, рассмотрим магазин В2, которому требуется 100-50=50 единиц товара. Направим их туда.

Заметим, на складе А2 осталось еще 200-50=150 единиц груза, которые мы распределим по магазинам В3 и В4, полностью удовлетворяя и их потребности.
Склады пусты!
Потребности магазинов в товаре полностью выполнены!
Получен опорный (первоначальный) план транспортной задачи.

Рассмотрели северо-западный метод построения первоначального плана (опорного решения).
Далее опишем метод минимальных стоимостей получения опорного плана.
Метод минимальных стоимостей получения опорного плана
Суть метода состоим в том, чтобы в первую очередь направлять груз в те пункты, где «расценки» в матрице стоимостей минимальны. Если клеток с наименьшими тарифами несколько, то заполняется любая из них.

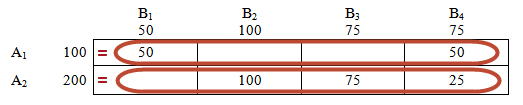
Направляем 100 единиц груза из склада А2 в магазин В2.
Остатки на складе А2 — 100 единиц. Потребности магазина В2 выполнены.
Груз со склада А2 отправим в магазин, у которого стоимость перевозки ниже — магазин В3, так как мин(4;7)=4
Размер поставки равен потребности магазина — 75. Остатки со склада 200-100-75=25 перенесем в магазин В4.

Остается только раскидать груз со склада А1 по магазинам: В1 — 50 единиц, В4 — 75-25=50 единиц.
Получили два опорных плана: методом северо-западного угла и методом минимальных стоимостей.
Первый опорный план (по методу северо-западного угла):
Второй опорный план (по методу минимальных стоимостей):
Далее проверим правильность вычисления первоначального плана.
Проверка правильности вычисления первоначального плана
Перед тем как перейти к дальнейшему решению задачи проверим условие:
Правило:
Количество заполненных клеток (базисных клеток) в первоначальном плане ВСЕГДА должно быть равно m + n — 1, где m — количество строк, n — количество столбцов
В нашем случае условие выполняется: 2 + 4 — 1 = 5
Что же делать, если количество заполненных ячеек меньше необходимого?
Подробно об этом с разбором примеров в статье Вырожденность опорного плана транспортной задачи. Как избавиться?
Во избежании случайных вычислительных ошибок проверим, равны ли суммарные значения каждой строки и каждого столбца соответствующим значениям условия.
100 = 50 + 50
200 = 100 + 75 + 25
По столбцам:
Видим, суммарные значения элементов каждого столбца равны соответствующим потребностям магазинов.
Несмотря на то, что опорные планы разные, оба приведут к одному оптимальному решению или же к решениям, имеющим одну стоимость перевозки.
Далее применим метод потенциалов к обоим опорным планам и сравним получившиеся ответы.
Метод потенциалов решения транспортной задачи — шаг 1.
Описанную ниже последовательность действий будем повторять несколько раз, с каждым шагом приближаясь к оптимальному решению. Начнем с проверки опорного плана на оптимальность.
Выпишем матрицу стоимостей, данную в условии задачи.
Далее строим рядом две таблицы. Размерность таблиц как и в матрице стоимостей:
количество строк = количеству складов, количество столбцов = количеству магазинов.
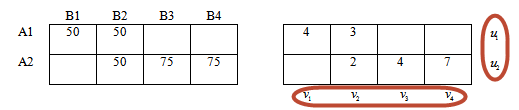
Заполняем первую — левую таблицу в соответствии с полученным опорным планом.

Переходим в правую таблицу.
Переносим из матрицы стоимостей значения, которые соответствуют занятым клеткам левой таблицы.
В матрице стоимости эти значения подчеркнуты.
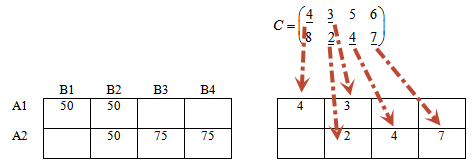
Припишем каждой строке правой таблице потенциалы u1, u2. Каждому столбцу — потенциалы v1, v2, v3, v4.
Для вычисления этих потенциалов в некоторых учебниках составляют систему и из нее определяют неизвестные (покажу на данном шаге).
Мы будем определять значения потенциалов непосредственно из правой таблицы.
Составим систему уравнений по следующему правилу:
Каждое из значений в ячейке (правая таблица) равно сумме потенциалов соответствующей строки и соответствующего столбца.
Например: значение 4 находится в 1-й строке и 1-м столбце. Тогда сумма потенциалов 1-й строки (u1) и 1-ого столбца(v1) равна 4.
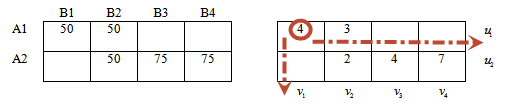
Первое уравнение системы: u1 + v1 = 4
Рассмотрим следующее значение таблицы.
Значение 3 находится в первой строке (потенциал u1), втором столбце (потенциал v2).
Второе уравнение системы: u1 + v2 = 3
Аналогично для каждого значения таблицы составим уравнение.
Получим систему уравнений:
Для того, чтобы система имела единственное решение, примем значение одного из потенциалов равным нулю.
Для удобства в качестве этого потенциала всегда будем брать v4.
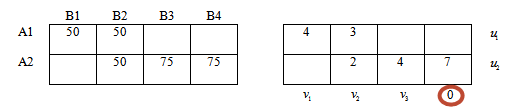
Тогда система уравнений будет выглядеть:
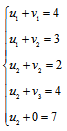
Решим систему уравнений и получим значения потенциалов:
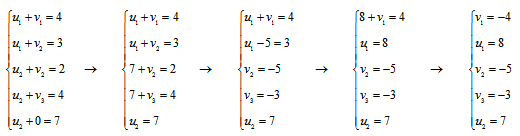
Наглядно:

Так как система очень проста, то значения потенциалов можно получить и устно.
Покажем подробно:
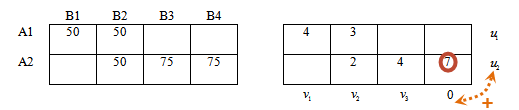
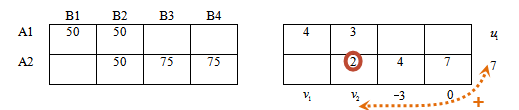
Сумма отмеченных потенциалов равна 7, следовательно, потенциал u2 = 7
Значение 4 базисной ячейки находится во 2-й строке, 3-м столбце, тогда рассмотрим сумму соответствующих потенциалов.
v3 + 7 = 4 откуда v3 = -3
Далее все аналогично:
Значение 2 равно сумме потенциалов 2-й строки и 2-го столбца:
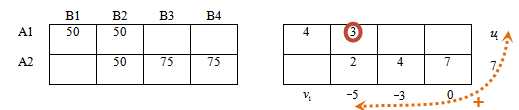
2 = v2 + 7 откуда v2 = -5
u1 — 5 = 3, откуда u1 = 8
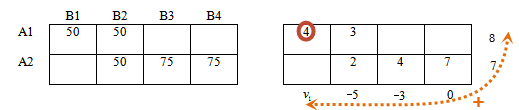
v1 + 8 = 4, откуда v1 = -4
В итоге получили:
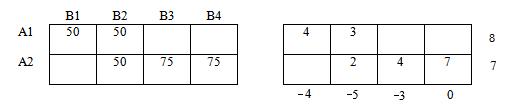
Далее приступим к заполнению пустых ячеек (свободные ячейки) правой таблицы.
Свободные ячейки подчиняются тому же правилу суммирования потенциалов.
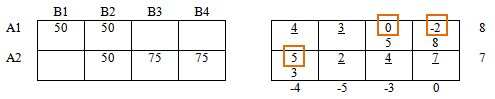
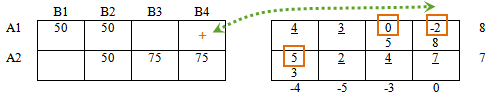
Вычислим оценочную матрицу, по которой узнаем, оптимален ли рассматриваемый план.
Из каждого элемента матрицы стоимостей вычтем соответствующий элемент правой таблицы:
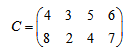 |
— | 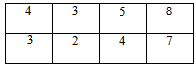 |
= |  |
Получили оценочную матрицу. Заметим, что в базисных ячейках всегда получим нули.
Критерий оптимальности:
если в оценочной матрице нет отрицательных элементов, то решение оптимально, в противном случае решение не оптимально.
Согласно критерию оптимальности, решение выше не оптимально, так как в оценочной таблице присутствует отрицательное значение.
Дабы не загромождать решение множеством таблиц, оценочная матрица в нашем решении будет «вписана» в правую таблицу.
Подчеркнутые значения — базисные ячейки, как сказано выше, значения оценочной матрицы в базисных ячейках равны нулю, нули писать не будем. Выделенные значения — значения оценочной матрицы в свободных ячейках, среди них ищем отрицательные значения.
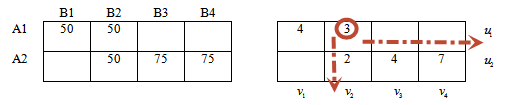
Для перехода к следующему опорному решению выполним следующее (построим цикл пересчета):
— найдем среди отрицательных значений оценочной матрицы максимальный по модулю (или по другому, минимальный среди отрицательных)
— в соответствующей ячейке левой таблицы ставим знак » + «
В нашем примере наименьшее отрицательное значение -2.
Знак » + » ставим в ячейке 1-й строки, 4-го столбца левой таблицы — ячейка соответствующая значению (-2).
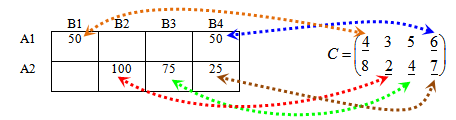
Необходимо расставить чередующиеся значения «+ » и » — » в левой таблице так, чтобы получился замкнутый цикл и выполнялись правила:
— остальные знаки цикла (все кроме уже поставленного первого » + «) ставим только в заполненных (базисных) ячейках таблицы,
— если в строке есть «плюс» («минус»), то в этой строке должен быть и «минус» («плюс»),
— если в столбце есть » плюс» («минус»), то в этом столбце должен быть и «минус» («плюс»).
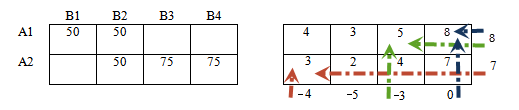
Применим к нашей таблице:
В столбце В4 есть «плюс», следовательно в этом столбце должен быть и «минус».
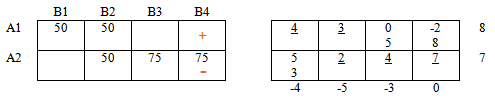
Аналогично, в строке А2 есть «минус», следовательно должен быть и «плюс».
Если мы поставим этот «плюс» в столбце В3, то цепочка порвется, так как в этом же столбце невозможно поставить «минус» — нет заполненной ячейки.
Ставим » + » в столбце В2 и продолжаем чередовать знаки.
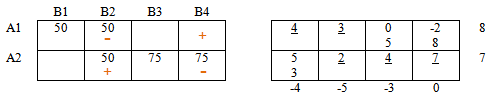
Получили замкнутый цикл чередующихся знаков. Цикл пересчета найден!
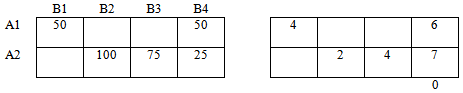
Далее обратимся к ячейкам, содержащим «минусы». Среди значений этих ячеек найдем минимальное: Δ = мин {50;75} = 50
К «плюсам» прибавим найденное Δ = 50, в ячейках с «минусами» — вычтем Δ = 50.
Ячейка, в которой находилось значение Δ = 50 останется пустой. В ячейке в которой мы поставили первый плюс появится значение, равное Δ = 50.
Общее количество заполненных (базисных) ячеек при пересчете не должно изменится!
Получили следующий опорный план:
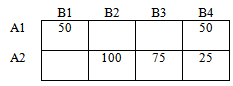
Вычислим стоимость перевозки на первом шаге.
Для этого найдем сумму произведений значений опорного плана и матрицы стоимостей.
S1 = 50 · 4 + 100 · 2 + 75 · 4 + 25 · 7 + 50 · 6 = 1275
На первом шаге решения транспортной задачи получили опорный план:

Общая стоимость перевозки S1 = 1275
Метод потенциалов — шаг 2
Алгоритм проверки плана на оптимальность и построение цикла пересчета очень подробно расписан в шаге 1.
Далее решение задачи будем излагать менее детально.
Для полученного опорного решения строим вспомогательную — правую таблицу и заполняем значениями из матрицы стоимостей базисные ячейки.
Вычисляем потенциалы строк и столбцов:
По правилу суммирования соответствующих потенциалов, заполняем свободные ячейки.
Вычисляем оценочные значения в свободных ячейках.
Для этого из значений матрицы стоимостей вычитаем найденные значения соответствующих свободных ячеек.
Среди оценочных значений нет отрицательных, следовательно план перевозки оптимален.
Получили оптимальный план. Итоговая стоимость перевозки S1 = 1275
Примеры решения транспортных задач:
Закрытая транспортная задача размерностью 2х2
Закрытая транспортная задача размерностью 3х4
Закрытая транспортная задача размерностью 2х3
Закрытая транспортная задача размерностью 4х5












 ,
, ,
,





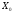
 .
. .
.
 из
из ,
, для
для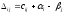 .
.
 ,
, является
является ,
,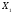 ,
,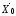 улучшить, выбирают среди отрицательных
улучшить, выбирают среди отрицательных







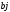




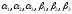


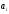
 =0
=0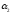 =-2
=-2 =-4
=-4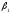 =1
=1 =3
=3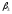 =1
=1





 +
+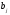







 =0
=0 =
= =
= =1
=1 =3
=3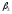 =2
=2