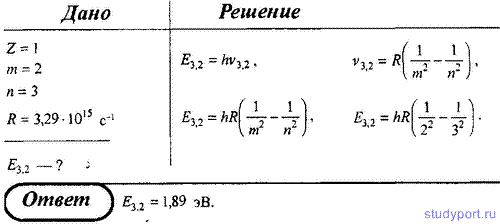Как найти минимальную энергию фотона

Страница 1 из 2

6. Элементы квантовой физики атомов, молекул и твердых тел

1. Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.

2. Определите максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера).

3. Определите длину волны λ, соответствующую второй спектральной линии в серии Пашена.

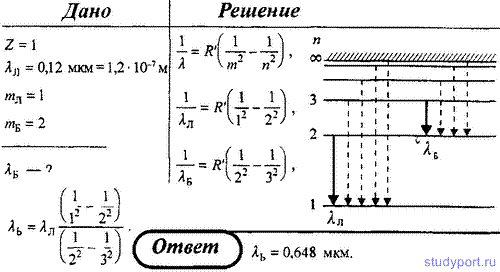
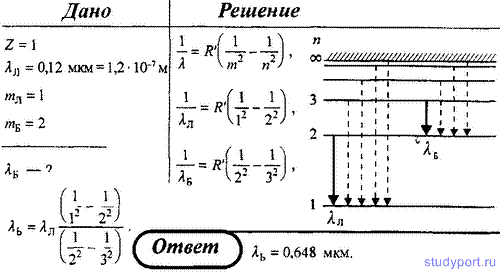
4. Максимальная длина волны спектральной водородной линии серии Лаймана равна 0,12 мкм. Предполагая, что постоянная Ридберга неизвестна, определите максимальную длину волны линии серии Бальмера.

5. Определите длину волны спектральной линии, соответствующей переходу электрона в атоме водорода с шестой боровской орбиты на вторую. К какой серии относится эта линия и какая она по счету?

6. Определите длины волн, соответствующие: 1) границе серии Лаймана; 2) границе серии Бальмера; 3) границе серии Пашена. Проанализируйте результаты.

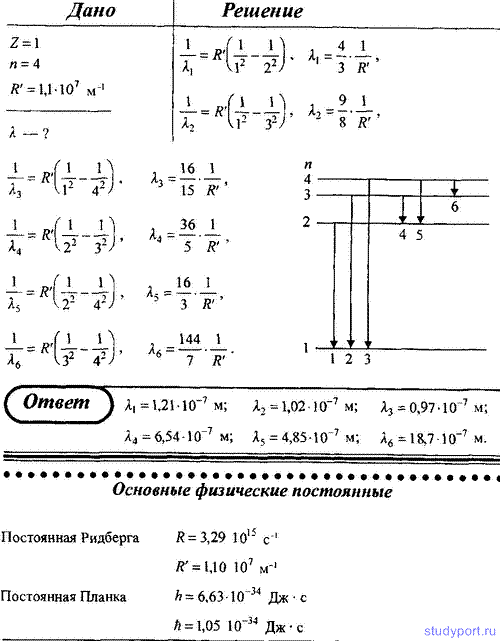
7. Атом водорода находится в возбужденном состоянии, характеризуемом главным квантовым числом n = 4. Определите возможные спектральные линии в спектре водорода, появляющиеся при переходе атома из возбужденного состояния в основное.

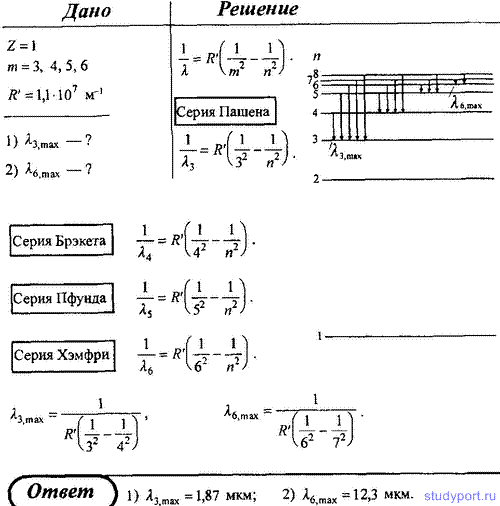
8. В инфракрасной области спектра излучения водорода обнаружено четыре серии—Пашена, Брэкета, Пфунда и Хэмфри. Запишите спектральные формулы для них и определите самую длинноволновую линию: 1) в серии Пашена; 2) в серии Хэмфри.

9. Определите число спектральных линий, испускаемых атомарным водородом, возбужденным на n-й энергетический уровень.

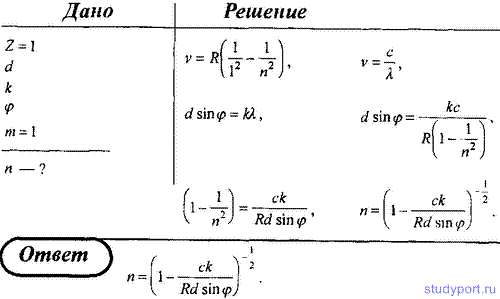
10. На дифракционную решетку с периодом d нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Оказалось, что в спектре дифракционный максимум k-го порядка, наблюдаемый под углом φ, соответствовал одной из линий серии Лаймана. Определите главное квантовое число, соответствующее энергетическому уровню, с которого произошел переход.

11. Используя теорию Бора для атома водорода, определите: 1) радиус ближайшей к ядру орбиты (первый боровский радиус); 2) скорость движения электрона по этой орбите.

12. Определите, на сколько изменилась энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ = 4,86*10^-7 м.

13. Определите длину волны λ спектральной линии, излучаемой при переходе электрона с более высокого уровня энергии на более низкий уровень, если при этом энергия атома уменьшилась на ΔE = 10 эВ.

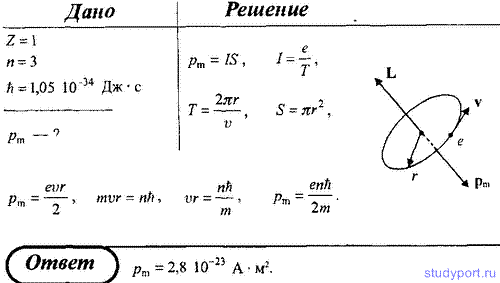
14. Используя теорию Бора, определите орбитальный магнитный момент электрона, движущегося по третьей орбите атома водорода.

15. Определите изменение орбитального механического момента электрона при переходе его из возбужденного состояния в основное с испусканием фотона с длиной волны λ = 1,02*10^-7 м.

16. Позитроний — атомоподобная система, состоящая из позитрона и электрона, вращающегося относительно общего центра масс. Применяя теорию Бора, определите минимальные размеры подобной системы.

17. Предполагая, что в опыте Франка и Герца вакуумная трубка наполнена не парами ртути, а разреженным атомарным водородом, определите, через какие интервалы ускоряющего потенциала φ возникнут максимумы на графике зависимости силы анодного тока от ускоряющего потенциала.

19. Докажите, что энергетические уровни атома водорода могут быть описаны выражением E_n = -2πh/n², где R — постоянная Ридберга.

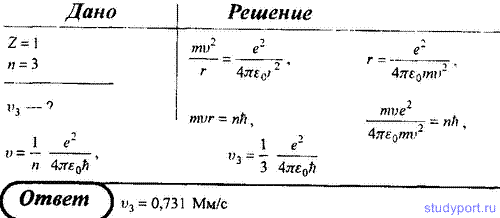
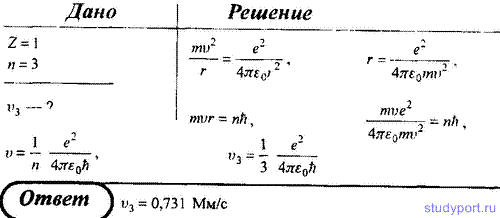
20. Определите скорость v электрона на третьей орбите атома водорода.

Источник

From Wikipedia, the free encyclopedia

Photon energy is the energy carried by a single photon. The amount of energy is directly proportional to the photon’s electromagnetic frequency and thus, equivalently, is inversely proportional to the wavelength. The higher the photon’s frequency, the higher its energy. Equivalently, the longer the photon’s wavelength, the lower its energy.

Photon energy can be expressed using any unit of energy. Among the units commonly used to denote photon energy are the electronvolt (eV) and the joule (as well as its multiples, such as the microjoule). As one joule equals 6.24 × 10¹⁸ eV, the larger units may be more useful in denoting the energy of photons with higher frequency and higher energy, such as gamma rays, as opposed to lower energy photons as in the optical and radio frequency regions of the electromagnetic spectrum.

Formulas[edit]

Physics[edit]

Photon energy is directly proportional to frequency.^[1]

where

This equation is known as the Planck–Einstein relation.

Additionally,

${displaystyle E={frac {hc}{lambda }}}$

where

E is photon energy
λ is the photon’s wavelength
c is the speed of light in vacuum
h is the Planck constant

The photon energy at 1 Hz is equal to 6.62607015 × 10⁻³⁴ J

That is equal to 4.135667697 × 10⁻¹⁵ eV

Electronvolt[edit]

Energy is often measured in electronvolts.

To find the photon energy in electronvolts using the wavelength in micrometres, the equation is approximately

${displaystyle E{text{ (eV)}}={frac {1.2398}{lambda {text{ (μm)}}}}}$

This equation only holds if the wavelength is measured in micrometers.

The photon energy of near infrared radiation at 1 μm wavelength is approximately 1.2398 eV.

Examples[edit]

An FM radio station transmitting at 100 MHz emits photons with an energy of about 4.1357 × 10⁻⁷ eV. This minuscule amount of energy is approximately 8 × 10⁻¹³ times the electron’s mass (via mass-energy equivalence).

Very-high-energy gamma rays have photon energies of 100 GeV to over 1 PeV (10¹¹ to 10¹⁵ electronvolts) or 16 nanojoules to 160 microjoules.^[2] This corresponds to frequencies of 2.42 × 10²⁵ to 2.42 × 10²⁹ Hz.

During photosynthesis, specific chlorophyll molecules absorb red-light photons at a wavelength of 700 nm in the photosystem I, corresponding to an energy of each photon of ≈ 2 eV ≈ 3 × 10⁻¹⁹ J ≈ 75 k_BT, where k_BT denotes the thermal energy. A minimum of 48 photons is needed for the synthesis of a single glucose molecule from CO₂ and water (chemical potential difference 5 × 10⁻¹⁸ J) with a maximal energy conversion efficiency of 35%.

References[edit]

^ «Energy of Photon». Photovoltaic Education Network, pveducation.org.
^ Sciences, Chinese Academy of. «Observatory discovers a dozen PeVatrons and photons exceeding 1 PeV, launches ultra-high-energy gamma astronomy era». phys.org. Retrieved 2021-11-25.

Источник

Фотоны

Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.
Энергия фотона
Импульс фотона
Давление света
Двойственная природа света

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.

В результате исследования явлений, связанных с взаимодействием света и вещества (тепловое излучение и фотоэффект), физики пришли к выводу, что свет состоит из отдельных порций энергии — фотонов. Излучение света, его распространение и поглощение происходит строго этими порциями.

Фотоны обладают энергией и импульсом и могут обмениваться ими с частицами вещества (скажем, с электронами или атомами). При этом мы говорим о столкновении фотона и частицы. При упругом столкновении фотон меняет направление движения — свет рассеивается. При неупругом столкновении фотон поглощается отдельной частицей или совокупностью частиц вещества — так происходит поглощение света.

Словом, фотон ведёт себя как частица и поэтому — наряду с электроном, протоном, нейтроном и некоторыми другими частицами — причислен к разряду элементарных частиц.

к оглавлению ▴

Энергия фотона

Выражение для энергии фотона с частотой мы уже знаем:

(1)

Часто бывает удобно работать не с обычной частотой , а с циклической частотой .

Тогда вводят другую постоянную Планка «аш с чертой»:

$h^{mkern -14mu -} = frac{displaystyle h}{displaystyle 2 pi vphantom{1^a}} = 1,05 cdot 10^{-34}$ Дж · с.

Выражение (1) для энергии фотона примет вид:

$E = h^{mkern -14mu -} omega.$

Фотон движется в вакууме со скоростью света и потому является релятивистской частицей: описывая фотон, мы должны привлекать формулы теории относительности. А там имеется такая формула для энергии тела массы , движущегося со скоростью :

$E = frac{displaystyle mc^2}{displaystyle sqrt{1 - frac{displaystyle v^2}{displaystyle c^2vphantom{1^a}}} vphantom{1^a}}.$ (2)

Если предположить, что m neq 0 , то формула (2) приводит к бессмысленному заключению: энергия фотона должна быть бесконечной. Чтобы избежать этого противоречия, остаётся признать, что масса фотона равна нулю. Формула (2) позволяет сделать и более общий вывод: только безмассовая частица может двигаться со скоростью света.

к оглавлению ▴

Импульс фотона

Обладая энергией, фотон должен обладать и импульсом. Действительно, важнейшая формула теории относительности даёт связь энергии и импульса частицы:

(3)

Для фотона, имеющего нулевую массу, эта формула сводится к простому соотношению:

E = pc.

Отсюда для импульса фотона получаем:

$p = frac{displaystyle E}{displaystyle cvphantom{1^a}} = frac{displaystyle h nu}{displaystyle cvphantom{1^a}}.$ (4)

Направление импульса фотона совпадает с направлением светового луча.

Учитывая, что отношение c/ nu есть длина волны lambda , формулу (4) можно переписать так:

$p =frac{displaystyle h}{displaystyle lambda vphantom{1^a}}.$ (5)

В видимом диапазоне наименьшими значениями энергии и импульса обладают фотоны красного света — у них самая маленькая частота (и самая большая длина волны). При движении в сторону фиолетового участка спектра энергия и импульс фотона линейно возрастают с частотой.

к оглавлению ▴

Давление света

Свет оказывает давление на освещаемую поверхность. Такой вывод был сделан Максвеллом из теоретических соображений и получил экспериментальное подтверждение в знаменитых опытах П.Н. Лебедева. Если понимать
свет как поток фотонов, обладающих импульсом , то можно легко объяснить давление света и вывести формулу Максвелла.

Предположим, что на некоторое тело падает свет частоты . Лучи направлены перпендикулярно поверхности тела; площадь освещаемой поверхности равна (рис. 1).

Рич. 1. Давление света

Пусть — концентрация фотонов падающего света, то есть число фотонов в единице объёма.

За время на нашу поверхность попадают фотоны, находящиеся внутри цилиндра высотой .

Их число равно:

При падении света на поверхность тела часть световой энергии отражается, а часть — поглощается. Пусть — коэффициент отражения света; величина r < 1 показывает, какая часть световой энергии отражается от поверхности. Соответственно, величина 1 - r — это доля падающей энергии, поглощаемая телом.

Как мы теперь знаем, энергия света пропорциональна числу фотонов. Поэтому можно написать, какое количество фотонов (из общего числа ) отразится от поверхности, а какое — поглотится ею:

$N_{o} = rN, N_{n} = (1 - r)N.$

Импульс каждого падающего фотона равен . Поглощённый фотон испытывает неупругое столкновение с телом и передаёт ему импульс . Отражённый фотон после упругого столкновения меняет направление своего импульса на противоположное, и поэтому импульс, переданный телу отражённым фотоном, равен .

Таким образом, от каждого фотона, входящего в световой поток, тело получает некоторый импульс. Вот простая и очевидная причина того, что свет оказывает давление на освещаемую поверхность.

Суммарный импульс, полученный телом от падающих фотонов, равен:

На нашу поверхность действует сила , равная импульсу, полученному телом в единицу времени:

$F = frac{displaystyle P}{displaystyle t vphantom{1^a}} = (1 + r)p frac{displaystyle N}{displaystyle tvphantom{1^a}} = (1 + r) frac{displaystyle h nu}{displaystyle cvphantom{1^a}} frac{displaystyle nSct}{displaystyle tvphantom{1^a}} = (1 + r)h nu nS.$

Давление света есть отношение этой силы к площади освещаемой поверхности:

$p_{CB} = frac{displaystyle F}{displaystyle Svphantom{1^a}} = (1 + r)h nu n.$ (6)

Выражение h nu n имеет простой физический смысл: будучи произведением энергии фотона на число фотонов в единице объёма, оно равно энергии света в единице объёма, то есть объёмной плотности энергии . Тогда соотношение (6) приобретает вид:

$p_{CB} = (1 + r)w.$

Это и есть формула для давления света, теоретически выведенная Максвеллом (в рамках классической электродинамики) и экспериментально проверенная в опытах Лебедева.

к оглавлению ▴

Двойственная природа света

В результате рассмотрения всей совокупности оптических явлений возникает естественный вопрос: что же такое свет? Непрерывно распределённая в пространстве электромагнитная волна или поток отдельных частиц — фотонов? Теория и эксперименты приводят к заключению, что оба ответа должны быть утвердительными.

1. Явления интерференции и дифракции света, характерные для любых волновых процессов, не оставляют сомнений в том, что свет есть форма волнового движения материи.

Таким образом, мы должны признать: да, свет имеет волновую природу, свет — это электромагнитная волна.

2. Однако явления взаимодействия света и вещества (например, фотоэффект) указывают на то, что свет ведёт себя как поток отдельных частиц. Эти частицы — фотоны — ведут, так сказать, самостоятельный образ жизни, обладают энергией и импульсом, участвуют во взаимодействиях с атомами и электронами. Излучение света — это рождение фотонов.

Распространение света — это движение фотонов в пространстве. Отражение и поглощение света — это соответственно упругие и неупругие столковения фотонов с частицами вещества.

Все попытки истолковать указанные явления излучения и поглощения света в рамках волновых представлений классической физики окончились неудачей. Оставалось лишь согласиться с тем, что свет имеет корпускулярную природу (от латинского слова corpusculum — маленькое тельце, частица), свет — это совокупность фотонов, мчащихся в пространстве.

Таким образом, свет имеет двойственную, корпускулярно-волновую природу — он может проявлять себя то так, то эдак. В одних явлениях (интерференция, дифракция) на передний план выходит волновая природа, и свет ведёт себя в точности как волна. Но в других явлениях (фотоэффект) доминирует корпускулярная природа, и свет ведёт себя подобно потоку частиц.

Странно всё это, не правда ли? Но что поделать — так устроена природа. Мы, люди, живём среди макроскопических тел, и наше воображение оказалось не способным полноценно представить себе явления микромира.
Природа, однако, неизмеримо шире и богаче того, что может вместить в себя человеческое воображение. Признав это и руководствуясь не столько собственным воображением, сколько наблюдениями, результатами экспериментов и весьма изощрённой математикой, люди начали успешно создавать квантовую теорию микроскопических явлений и процессов.

О некоторых парадоксальных на первый взгляд — но тем не менее подтверждённых экспериментально! — выводах квантовой теории мы поговорим в следующем листке.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Фотоны» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Теория атома водорода по Бору

1.
Определите энергию фотона, испускаемого
при переходе электрона в атоме водорода
с третьего энергетического уровня на
второй.

2.
Определите максимальную и минимальную
энергии фотона в видимой серии спектра
водорода (серии Бальмера).

3.
Определите длину волны λ, соответствующую
второй спектральной линии в серии
Пашена.

4.
Максимальная длина волны спектральной
водородной линии серии Лаймана равна
0,12 мкм. Предполагая, что постоянная
Ридберга неизвестна, определите
максимальную длину волны линии серии
Бальмера.

5.
Определите длину волны спектральной
линии, соответствующей переходу электрона
в атоме водорода с шестой боровской
орбиты на вторую. К какой серии относится
эта линия и какая она по счету?

6.
Определите длины волн, соответствующие:
1) границе серии Лаймана; 2) границе серии
Бальмера; 3) границе серии Пашена.
Проанализируйте результаты.

7.
Атом водорода находится в возбужденном
состоянии, характеризуемом главным
квантовым числом n = 4. Определите возможные
спектральные линии в спектре водорода,
появляющиеся при переходе атома из
возбужденного состояния в основное.

8.
В инфракрасной области спектра излучения
водорода обнаружено четыре серии—Пашена,
Брэкета, Пфунда и Хэмфри. Запишите
спектральные формулы для них и определите
самую длинноволновую линию: 1) в серии
Пашена; 2) в серии Хэмфри.

9.
Определите число спектральных линий,
испускаемых атомарным водородом,
возбужденным на n-й энергетический
уровень.

10.
На дифракционную решетку с периодом d
нормально падает пучок света от разрядной
трубки, наполненной атомарным водородом.
Оказалось, что в спектре дифракционный
максимум k-го порядка, наблюдаемый под
углом φ, соответствовал одной из линий
серии Лаймана. Определите главное
квантовое число, соответствующее
энергетическому уровню, с которого
произошел переход.

11.
Используя теорию Бора для атома водорода,
определите: 1) радиус ближайшей к ядру
орбиты (первый боровский радиус); 2)
скорость движения электрона по этой
орбите.

12.
Определите, на сколько изменилась
энергия электрона в атоме водорода при
излучении атомом фотона с длиной волны
λ = 4,86*10^-7м.

13.
Определите длину волны λ спектральной
линии, излучаемой при переходе электрона
с более высокого уровня энергии на более
низкий уровень, если при этом энергия
атома уменьшилась на ΔE = 10 эВ.

14.
Используя теорию Бора, определите
орбитальный магнитный момент электрона,
движущегося по третьей орбите атома
водорода.

15.
Определите изменение орбитального
механического момента электрона при
переходе его из возбужденного состояния
в основное с испусканием фотона с длиной
волны λ = 1,02*10^-7 м.

16.
Позитроний — атомоподобная система,
состоящая из позитрона и электрона,
вращающегося относительно общего центра
масс. Применяя теорию Бора, определите
минимальные размеры подобной системы.

17.
Предполагая, что в опыте Франка и Герца
вакуумная трубка наполнена не парами
ртути, а разреженным атомарным водородом,
определите, через какие интервалы
ускоряющего потенциала φ возникнут
максимумы на графике зависимости силы
анодного тока от ускоряющего потенциала.

19.
Докажите, что энергетические уровни
атома водорода могут быть описаны
выражением E_n =
-2πh/n²,
где R — постоянная Ридберга.

20.
Определите скорость v электрона на
третьей орбите атома водорода.

21.
Электрон находится на первой боровской
орбите атома водорода. Определите для
электрона: 1) потенциальную энергию E_п;
2) кинетическую энергию E_к;
3) полную энергию E.

22.
Определите частоту f вращения электрона
по третьей орбите атома водорода в
теории Бора.

23.
Определите: 1) частоту f вращения электрона,
находящегося на первой боровской орбите;
2) эквивалентный ток.

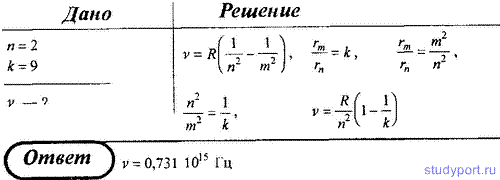
24.
Определите частоту света, излучаемого
атомом водорода, при переходе электрона
на уровень с главным квантовым числом
n = 2, если радиус орбиты электрона
изменился в k = 9 раз.

25.
Пользуясь теорией Бора, найдите числовое
значение постоянной Ридберга.

26.
Определите потенциал ионизации атома
водорода.

27.
Основываясь на том, что энергия ионизации
атома водорода E_i =
13,6 эВ, определите первый потенциал
возбуждения φ₁ этого
атома.

28.
Определите первый потенциал возбуждения
атома водорода.

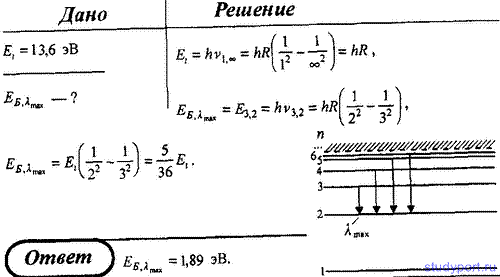
29.
Основываясь на том, что энергия ионизации
атома водорода E_i =
13,6 эВ, определите в электрон-вольтах
энергию фотона, соответствующую самой
длинноволновой линии серии Бальмера.

30.Основываясь
на том, что первый потенциал возбуждения
атома водорода φ₁ =
10,2 В, определите в электрон-вольтах
энергию фотона, соответствующую второй
линии серии Бальмера.

31.
Определите работу, которую необходимо
совершить, чтобы удалить электрон со
второй боровской орбиты атома водорода
за пределы притяжения его ядром.

32.
Электрон выбит из атома водорода,
находящегося в основном состоянии,
фотоном, энергия которого ε = 17,7 эВ.
Определите скорость ν электрона за
пределами атома.

33.
Фотон с энергией ε = 12,12 эВ, поглощенный
атомом водорода, находящимся в основном
состоянии, переводит атом в возбужденное
состояние. Определите главное квантовое
число этого состояния.

34.
Определите, какие спектральные линии
появятся в видимой области спектра
излучения атомарного водорода под
действием ультрафиолетового излучения
с длиной волны λ = 95 нм.

35.
В излучении звезды обнаружен
водородоподобный спектр, длины волн
которого в 9 раз меньше, чем у атомарного
водорода. Определите элемент, которому
принадлежит данный спектр.

36.
Применяя теорию Бора к мезоатому водорода
(в мезоатоме водорода электрон заменен
мюоном, заряд которого равен заряду
электрона, а масса в 207 раз больше массы
электрона), определите: 1) радиус первой
орбиты мезоатома; 2) энергию ионизации
мезоатома.

37.
Определите, какая энергия требуется
для полного отрыва электрона от ядра
однократно ионизованного атома гелия,
если: 1) электрон находится в основном
состоянии; 2) электрон находится в
состоянии, соответствующем главному
квантовому числу n = 3 .

Соседние файлы в предмете Физика

#
#
#

01.11.201630.14 Кб24Оптика.txt
#

12.10.201644.99 Кб27тест8.txt

Источник

На основании базовых положений статистической физики и принципа наименьшего действия вычислено уравнение распада фотона.
Определена нижняя граница существования фотонов по энергии. Рассмотрен процесс уменьшения энергии фотона во времени.
Исследован процесс формирования космического фона излучения в результате “ распада “ фотона до граничной частоты 〖10〗^12 с^(-1). Обоснован эффект красного смещения космических излучений до значений микроволнового фона.

В вычислениях траектории фотона использованы впервые координаты (E,t, энергия и время, то есть v-t). Традиционный метод использует обобщенные координаты ( q,p, координата, импульс). Применение координатного пространства (E-t) для фотона позволяет решить задачи, поставленные в предполагаемых работах.
Важным доводом также являются соотношения неопределенности Гейзенберга:

удовлетворяющие взаимной корреляции и соответствию. Второе из них наиболее значимо в силу ранее высказанных соображений. Чтобы изначально объяснить логику, предлагаемую в работах определим главные положения в исследовании:

Принцип наименьшего действия

Распределение тождественных частиц – фотонов по энергии в соответствии с законом Бозе-Эйнштейна ( Б-Э)

Поясним первое из них. Собственно Действие, как физическая величина, с размерностью (Дж – сек) представлена в неравенствах Гейзенберга и в практике Вариационного исчисления вычисляется минимальное значение этой величины, однако в предлагаемом исследовании впервые вычисления проведены в координатах (Е, t).

Модели формирования Вселенной основаны в основном на изменении частоты излучений в результате эффекта Доплера и факте реликтового излучения. Результаты исследований радиочастотного диапазона получили свое объяснение. Однако, нельзя признать, что существует логически стройная теория образования Вселенной, основанная на предположении Большого Взрыва, никак экспериментально не доказанного, т.к. «разлет Галактик» основан лишь на изменении частоты измеряемых фотонов, но как будет установлено далее изменение частоты связано с распадом фотонов.

Под вакуумом предполагается пространство, лишённое материи, заполненное энергией нулевых колебаний [1] реализуемых системой бозонов — фотонов. Строго говоря, это тоже материя, поэтому для большей корректности определим вакуум как пространство, заполненное энергией в виде фотонов при полном отсутствии частиц, с которыми возможно взаимодействие фотона. Важным для дальнейшего исследования является следующее: взаимодействие фотонов проявляется в формировании распределения фотонов по энергии — статистике Бозе – Эйнштейна. (далее Б – Э).

Рассматривается явление образования «ансамбля» фотонов из первичного кванта при потере первичным фотоном энергии и переходе в новое состояние hν₁ (ν₁<ν₀) далее hν₂ и т.д. Так как у световых квантов нет времени, то процесс описанного изменения и образования ансамбля ν_ө, ν₁ … происходит одновременно в системе фотонов, в том числе взаимодействие вторичных фотонов подчиняется статистике бозонов.

ВЫЧИСЛЕНИЕ УРАВНЕНИЯ РАСПАДА ФОТОНА[править]

В координатах ν — частота, t – время исследован функционал [1, 2]:

${displaystyle t[v(t)]=int limits _{0}^{infty }{frac {sqrt {1+(v^{1})^{2}}}{v^{1}}}dt}$

так что ${displaystyle delta int F(v^{1},t)dt=delta int {frac {sqrt {1+(v^{1}).^{2}}}{v^{1}}}dt=0}$

Соответственно, уравнение Эйлера [2]

${displaystyle F_{v}-{frac {d}{dt}}F_{v^{1}}=0}$

в котором Fv = 0, следовательно:

${displaystyle {frac {d}{dt}}left({frac {d}{dv^{1}}}left({frac {sqrt {1+(v^{1})^{2}}}{v^{1}}}right)right)=0}$

Окончательно полученный результат включает два уравнения:

${displaystyle {frac {d^{2}v}{dt^{2}}}=0}$ и ${displaystyle 3left({frac {dv}{dt}}right)^{2}+2=0}$ (1)

Решение находим из первого уравнения

${displaystyle v=C_{2}t+C_{1}}$ когда t = 0, ν = ν₀, то ${displaystyle v=ct+c_{0}}$ (2)

Для определения постоянной C₂ рассмотрим распределение Б – Э. Следует отметить: энергия фотона при движении изменяется, образуя (в системе координат фотонов, где t = 0 ) «ансамбль» вторичных фотонов в соответствии с Б – Э распределением [3]

${displaystyle dn={frac {Z-1}{exp {frac {varepsilon }{kT}}-1}}}$

Единицей в числителе можно пренебречь в силу малости по сравнению с Z — числом фазовых ячеек:

${displaystyle Z={frac {dvarepsilon dt}{h}}={frac {hdvdt}{h}}=dvdt}$ (3)

h – объём фазовой ячейки.

Из ( 1 ) для энергии : hν = c₂ht + hν₀ = c₂ht +ε₀ = ε

Тогда: ${displaystyle dn={frac {dvdt}{exp left({frac {C_{2}ht+varepsilon _{0}}{kT}}right)-1}}}$

По условию нормировки:

${displaystyle n=int _{sigma _{0}}^{0}dvint _{0}^{infty }{frac {dt}{exp left({frac {C_{2}ht+varepsilon _{0}}{kT}}right)}}=1}$ (4)

Отсутствие единицы в знаменателе обосновано тем, что ${displaystyle exp {frac {hv}{kT}}>>1}$

Вычисление интегралов в ( 4 ) приводит к значению n:

${displaystyle n=-v_{0}left(-{frac {kT}{C_{2}h}}right)exp left(-{frac {varepsilon _{0}}{kT}}right)exp left(-{frac {C_{2}ht}{kT}}|_{0}^{infty }right)=-v_{0}{frac {kT}{C_{2}h}}exp left(-{frac {varepsilon _{0}}{kT}}right)}$ (5)

Выполняя условия нормировки n=1 , находим

${displaystyle C_{2}=-v_{0}{frac {kT}{h}}exp left(-{frac {varepsilon _{0}}{kT}}right)}$

Подставляя в ( 2 ) :

${displaystyle v=v_{0}-v_{0}({frac {kT}{h}}exp left(-{frac {hv}{kT}}right))t}$ (6)

для энергии

${displaystyle varepsilon =varepsilon _{0}(1-({frac {kT}{h}}exp left(-{frac {varepsilon _{0}}{kT}}right))t)}$ (7)

Итак, уменьшение частоты фотона в вакууме определяется (6) ,

Линейная зависимость отражает явление уменьшения энергии фотона при его движении, до какого – то предельного значения энергии ( 7). или нуля. При этом получается, что пространство заполнено фотонной средой с тенденцией уменьшения общей (суммарной) энергией вакуума с одной стороны и постоянным повышением – за счёт поступающих потоков световых квантов с другой.

Определяем время жизни t₁ фотона из ( 6 ) при:

ν = 0, ${displaystyle v_{0}(1-{frac {kT}{h}}t_{1}exp left(-{frac {hv}{kT}}right))=0}$

${displaystyle t_{1}={frac {h}{kT}}exp left({frac {h}{kT}}vright)=Delta e^{Delta v_{0}}}$ , где ${displaystyle Delta ={frac {h}{kT}}}$ (8)

Вычисление времени жизни фотона другим манером[править]

Рассмотрим распределение Б –Э в энергетическом аспекте.

Количество частиц в интервале энергий ( ε, ε + dε ), где dε<<ε

${displaystyle dn={frac {z-1}{exp {frac {varepsilon }{kT}}-1}}}$

При исследовании энергетического баланса (-1) в числителе принципиально важна.

Причём, полная энергия занятых уровней вторичными фотонами равна: hν₀, следовательно (при z = dνdt):

${displaystyle E=int _{0}^{t_{1}}dtint _{0}^{infty }{frac {hvdv}{exp {frac {hv}{kT}}-1}}-int _{0}^{infty }{frac {dvarepsilon }{exp {frac {varepsilon }{kT}}-1}}=hv._{0}}$ (9)

Верхний предел интегралов, строгости ради, должен быть ν₀, однако, не уменьшая общности, интегрируем до бесконечности, так как ν порядка ${displaystyle 10^{11}-10^{15}}$ , что при малости фазовой ячейки h ${displaystyle (10^{-34})}$ собственно и является бесконечным пределом, к тому же интегрирование функции вида e^x (x + 1) ( ${displaystyle x={frac {hv_{0}}{kT}}}$ при смене переменных ), даёт число в предельном значении 1, значение же интеграла равно ${displaystyle {frac {pi ^{2}}{6}}}$ , что в конечных вычислениях не влияет на правильность и строгость полученных далее результатов.

Также и со вторым интегралом в ( 9 ).

Первое слагаемое в ( 9 ) описывает энергию частиц, заполнивших все уровни фазового пространства, но так как возможности у одного фотона, размножающегося на вторичные при потере энергии, ограничены и из Zi фазовых ячеек (квантовых уровней) с ε₁ занята только одна, иначе быть не может, так как следующий фотон с энергией ε_j (ε_j < ε_j) займёт 1 квантовый уровень в фазовой ячейке и т. д., то следует признать, что энергия, размещённая в фазовом слое не равна энергии hν₀, размещённой по отдельным единичным уровням фазовой поверхности, реализуемой при dε →0.

Поэтому второй интеграл в ( 9 ), представляющий «внутреннюю» энергию распределения без учёта всех квантовых уровней фазового пространства Z, при вычитании восстанавливает равенство

${displaystyle hv_{0}=t_{1}int limits _{0}^{infty }{frac {(kT)^{2}h{frac {hv}{kT}}d{frac {hv}{kT}}}{h^{2}(exp {frac {hv}{kT}}-1)}}-(-kT)int limits _{0}^{infty }exp left(-{frac {varepsilon }{kT}}right)dleft(-{frac {varepsilon }{kT}}right)}$

${displaystyle hv_{0}={frac {pi ^{2}(kT)^{2}t_{1}}{6h}}-kT}$

Вычисляем время жизни:

${displaystyle t_{1}={frac {h}{kT}}left({frac {hv_{0}}{kT}}+1right)={frac {h}{kT}}e^{{frac {h}{kT}}v_{0}}={frac {h}{theta }}e^{{frac {h}{theta }}v_{0}}}$ (10)

Что совпадает с ( 8 ) , kt = .

Итак, предопределённость фотонов к распределению Бозе – Эйнштейна позволяет вычислить время жизни фотона в вакууме двумя различными способами — (8) и (10), также найти зависимость энергии фотона от времени.

Необходимо подчеркнуть: в координатной T-системе фотона образования ансамбля вторичных фотонов из первичного происходит одновременно для всех фотонов hν₀ > hν₁ …из за отсутствия времени в T-системе, в отличии от координаты t, из которой этот процесс исследуется и в которой фиксируется только один фотон с убывающей энергией.

Энтропия и свободная энергия фотона. Определение кванта энергии при распаде.[править]

Исследуется необратимый статистический процесс в замкнутой системе подчинённый статистике Бозе – Эйнштейна (Б – Э) – в некотором смысле продолжение и развитие работ [ 5 ] – [ 6 ].

Энтропия S = k ln w для вероятностного процесса бозонов:

${displaystyle S=kln{frac {1}{exp {frac {hv}{kT}}-1}}=-klnleft(exp {frac {hv}{kT}}-1right)=-{frac {hv}{T}}}$ (11)

где: единица в скобках не существенна в силу её малости по сравнению с экспонентой.

Распределение Б –Э можно представить:

${displaystyle W={frac {1}{exp left({frac {S(t)}{k}}-1right)}}={frac {1}{exp left({frac {E(t)-F(t)}{theta }}-1right)}}}$ (12)

Где: величины E, F, энергия и свободная энергия связаны основным термодинамическими равенством E = F + TS, а модуль распределения ө = kt.

В (12) записаны функциональные зависимости S (t) и F (t), что указывает на дальнейшее рассмотрение динамического процесса.

Интеграл по всему фазовому пространству ∫ w dω = 1.

В координатах V частота t – время dw = dv dt [1] для распределения Б – Э (12):

${displaystyle int {frac {dvdt}{exp left({frac {E-F}{theta }}right)-1}}=1}$ (13)

Упраздняя единицу в знаменателе преобразуем к виду:

${displaystyle exp {frac {F}{theta }}int exp(-{frac {E}{theta }})dvdt=1}$

и далее логарифмируя:

${displaystyle -{frac {F}{theta }}lne=lnint exp left(-{frac {E}{theta }}right)dvdt}$

получаем статистическое выражение свободной энергии:

${displaystyle -F=theta lnint exp left(-{frac {E}{theta }}right)dvdt}$ (14)

вычисляем свободную энергию, точнее её наибольшую величину:

${displaystyle -F=theta ln(int _{0}^{t_{1}}dtint _{v_{0}}^{0}exp left(-{frac {hv}{theta }}right)dv)=hv._{0}}$ (15)

Где:

${displaystyle t_{1}={frac {h}{theta }}exp left({frac {hv}{theta }}right)}$ , ${displaystyle exp left(-{frac {hv}{theta }}right)sim 0}$ (16)

Итак, свободная энергия F, т.е. та энергия которая передаётся ансамблю вторичных фотонов по величине равна hvo, равна энергии первичного фотона.

Возвращаясь к равенству E = F + TS, получаем

${displaystyle hv_{0}=-hv_{0}+TS}$ , ${displaystyle TS=2hv_{0}}$ (17)

Предполагая дискретный характер «раздачи» энергии обозначим через m число актов «размножения» вторичных фотонов, что также позволяет вычислить время между образованием i и (i + 1) фотона в T-системе или переходу i – го фотона в (i + 1) в t — системе, т.е.:

${displaystyle {frac {t_{1}}{m}}={frac {h}{theta m}}exp({frac {h}{theta }}v_{0})}$ (18)

Подставляя этот результат в интеграл состояний в (14) и используя вычисления (15) :

${displaystyle -F=theta left(ln{frac {h}{theta m}}exp {frac {h}{theta }}v_{0}+ln{frac {theta }{h}}right)=theta (lnh-lntheta -lnm+{frac {h}{theta }}v_{0}+lntheta -lnh)}$

${displaystyle -F=-theta lnm+hv_{0}}$

Получаем: при F = O, hν₀ = ө lnm

Тогда : ${displaystyle m=exp {frac {hv_{0}}{theta }}.}$ Частота актов F определяется как m/t₁ .

${displaystyle f={frac {exp {frac {hv_{0}}{theta }}}{{frac {h}{theta }}exp {frac {hv_{0}}{theta }}}}={frac {theta }{h}}}$ (19)

Энергия «излучаемая» за 1 акт

${displaystyle E={frac {E_{0}}{m}}}$ ; ${displaystyle E_{0}={frac {hv_{0}}{exp {frac {hv_{0}}{theta }}}}}$ (20)

Учитывая, что

${displaystyle exp {frac {hv_{0}}{theta }}=1+{frac {hv_{0}}{theta }}}$ and ${displaystyle {frac {hv_{0}}{theta }}>>1}$

Получаем Eө = Ө (21)

— Квант энергии в формировании Б –Э

Определение связанной энергии при распаде[править]

Возвращаясь обозначенным F (t) и S (t) найдём эти зависимости от t, используя (14):

${displaystyle -F=0ln(int exp left(-{frac {hv}{theta }}right)dvdt)=0lnleft(t{frac {theta }{h}}left(exp ^{frac {hv_{0}}{theta }}-1right)right)=theta (lnleft({frac {theta }{h}}tright)+ln{bigl (}exp left(-{frac {hv_{0}}{theta }}-1right){bigr )})}$

Окончательно:

${displaystyle F=-theta lnleft({frac {theta }{h}}tright)}$ (22)

Представим равенство E = F + ST в виде:

${displaystyle {frac {theta S(t)}{k}}=hv-F(t)}$ (23)

энергия — hν₀ И воспользуемся равенством (22) для свободной энергии, причём полная, эта энергия заключена в ансамбле, созданном первичном фотоном.

Подставим (22) в (23), получаем: ${displaystyle {frac {theta }{k}}S(t)=hv_{0}+theta lnleft({frac {theta }{h}}tright)}$ (24)

или: ${displaystyle S(t)_{0}=S_{0}+kln({frac {theta }{h}}t)}$

где: ${displaystyle S_{0}={frac {khv_{0}}{theta }}={frac {hv_{0}}{T}}}$

Предельным значением t в (22) и (24) близким к нулю является:

${displaystyle t={frac {h}{theta }}={frac {1}{f}}}$

Тестовая проверка (24) при t = t₁, показывает:

${displaystyle S_{t_{1}}=S_{0}+klnleft({frac {theta h}{htheta }}exp left({frac {htheta _{0}}{theta }}right)right)=S_{0}+k{frac {htheta _{0}}{kT}}=S_{0}+S_{0}}$ (25)

Т.е. совпадает с (17) : S = 2S₀;.

Следует отметить: рассмотренное явление представляет статистический Закон Необратимого процесса в замкнутой системе с возрастающей энтропией.

В равенстве (23) ${displaystyle {frac {theta S}{k}}=TS}$ соответствует связанной энергии в ансамбле, в исследуемом явлении – это энергия, связанная в формировании статистического распределения: E_s = TS

${displaystyle E_{BOSE}=E_{S}=theta lnW=theta ln{frac {1}{exp {frac {hv}{theta }}-1}}=theta {Biggl (}-ln{Biggl (}exp {frac {hv}{theta }}-1{Biggr )}{Biggr )}}$

И окончательно: E_bose = ${displaystyle -hv_{0}}$ .

Следовательно, связанная энергия изменяется в соответствии с (7) :

${displaystyle E_{s}=-varepsilon _{0}{biggl (}1-{frac {kT}{h}}exp {biggl (}-{frac {varepsilon _{0}}{kT}}{biggr )}t{biggr )}}$ (26)

Итак, энергия первичного фотона не рассевается, а переходит в энергию связи между вторичными фотонами при формировании Б – Э распределении, т.е. представляет связанную энергию Бозе – Эйнштейна статистики через посредство квантов (21) Ө. В t–системе Ө-кванты никак не проявляются, т.к. захватываются связью в Б –Э распределении.

Определение модуля распределения[править]

В найденных параметрах «распадающегося» фотона присутствует термодинамическая величина КТ. В настоящем исследовании непосредственно не рассматривается механизм «распада» первичного фотона, в основе исследовании – принципы наименьшего действия, «фазовое» пространство (ν, t, частота и время), точнее ε и t, ( энергия и время ). Принципиальным является проблема Ө — модуля. Традиционное равенство KT = hν₀, неприменимо для фотона. Рассмотрим связь Ө с переменными распределения бозонов и фермионов.

Точка пересечения ε₁ распределений Бозе и Ферми:

${displaystyle {frac {z-1}{exp {frac {varepsilon _{1}}{theta }}-1}}={frac {2z}{exp {frac {varepsilon _{1}}{theta }}+1}}}$ , т.е. ${displaystyle e^{frac {varepsilon _{1}}{theta }}={frac {3z-1}{z+1}}={frac {3(z-{frac {1}{3}})}{z+1}}=3}$

где: ${displaystyle z-{frac {1}{3}}approx z+1}$ , следовательно ${displaystyle theta ={frac {varepsilon _{1}}{ln3}}}$ , величина ln 3 ~ 1,

окончательно Ө=ε₁.

Т. о. модуль распределения отождествляется с некоторой энергией (не с температурой) ε₁ в статистиках бозонов и фермионов.

Астрофизический аспект исследований[править]

Формулы, описывающие распад фотона могут быть преобразованы следующим образом:

— линейная зависимость энергии от времени

${displaystyle varepsilon =varepsilon _{0}{biggl (}1-{frac {t}{t_{1}}}{biggr )}}$ (27)

— время жизни фотона

${displaystyle t_{1}={frac {h}{theta }}e^{{frac {h}{theta }}v_{0}}}$

Итак, модуль распределения , входящий в формулу статистических распределений, традиционно обозначаемый кТ [ 2 ] , в сущности представляет некоторую общую энергию в распределениях Ферми и Бозе-Эйнштейна, также является квантом энергии связи в формировании Б-Э статистики бозонов и том энергии при распаде фотона с потерей величины энергии на каждом акте : ${displaystyle hv_{1}=hv_{0}-theta }$ , ${displaystyle hv_{2}=hv_{1}-theta }$ и т.д.

К сему, следует добавить следующее: постоянно встречающееся количество из двух констант ${displaystyle {frac {h}{theta }}}$ имеет размерность [c] и гипотетически может быть представлено как квант времени, наименьший допускаемый природой интервал времени: ${displaystyle q={frac {h}{theta }}}$ (возможно это время релаксации ${displaystyle -10^{-12}}$ c). Переход к квантованию времени позволяет утверждать, что, фундаментальные представления о квантовании электромагнитного излучения ограничены некоторым порогом , определяемым из формулы времени жизни фотона : принимая квант времени по величине равным времени релаксации и предположив ${displaystyle t=e10^{-12}}$ ( приблизительно ноль времени жизни фотона ) получаем ограничение по частоте излучения порядка ${displaystyle 10^{12}}$ колебаний в секунду – что близко к фону радиочастотного диапазона. Определим этот порог через – f.

Квантование излучения происходит не во всем диапазоне электромагнитных волн, а только в пространстве частот , ограниченных снизу , указанной величиной f , ниже этого значения происходит распространение волн. Распад фотона , уменьшение энергии, при достижении порога f завершается исчезновением кванта как частицы и далее энергия существует в виде волн.

Потенциальная энергия фотонного поля[править]

Рассмотрение энергетического баланса позволяет заключить , что энергия , излучаемая при каждом акте распада фотона , аккумулируется в энергию связи частиц Б – Э распределения т.е. с исчезновением фотона энергия переходит полностью в энергию потенциальную , обуславливающую энергию формирования распределения Б-Э , что справедливо как для T-системы трека фотона , так и для системы t-наблюдателя. Вероятно, существует связь между энергией нулевых колебаний и энергией квантов .

Для фотона постулированный дуализм волна – частица адекватен феномену ФОТОН в том смысле , что при энергиях выше порога f — корпускула, ниже – волна. Подобный ‘ дуализм “ c необходимостью приводит к рассмотрению проблемы эфира , т.к. “ чистый “ ( без полей и каких-либо сред ) вакуум, лишенный взаимодействий между фотонами , невозможен из-за принципиально важной для настоящего рассмотрения ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ [4] между фотонами :

${displaystyle U(v)=-theta ln(1+exp {biggl (}-{frac {hv}{theta }}{biggr )})}$ (28)

Формула ( 28 ) получена из рассмотрения функции U( r,T ) для тождественных частиц [ 1 ] при смене переменных и параметров соотносительно к фотону. Корректность преобразований и истинность формулы ( 28 ) подтверждается равенством по модулю производных по времени от энергии фотона ( 7 ) и потенциальной энергии ( 28 ), что находится в согласии с ранее полученным результатом о перекачке энергии фотона в потенциальную.

Поле потенциальной энергии фотонов является тем ‘эфиром’- средой , в которой фотон распространяется вначале как квант – частица, а после потери энергии , отданной эфиру, за порогом f — как волна.

Механизм возбуждения в эфире — образования фотона источником излучения в потенциальном поле — кванта энергии представляет тему дальнейших исследований.

Неудачные попытки объединения гравитационных, электромагнитных и ядерных сил позволяют предположить , что проблема , возможно, продвинется к решению ,если это универсальное поле ‘искать’ в потенциальном поле формирования распределения бозонов. Принятие гипотезы эфира в виде фотонного потенциального поля энергии, предположительно, является весьма продуктивной в свете: устранения бесконечностей в квантовой механике и формирования уравнения объединенного поля, имеющего решение

Следует заметить , что известные опыты по обнаружению эфира были обречены на неудачу. Как стало понятно в настоящее время.

Решение проблемы микроволнового фона. Гипотеза[править]

Итак, процесс формирования фона излучения в результате “ распада “ фотона до граничной частоты ${displaystyle 10^{12}}$ ${displaystyle c^{-1}}$ исследован на основе Вариационного принципа, свойства распределения бозонов и исследования энтропии и свободной энергии фотона. Предельное значение энергии ${displaystyle 10^{-22}}$ Дж. ( ${displaystyle 10^{12}}$ ${displaystyle c^{-1}}$ ) , при котором фотон существует как квант, определяет энергию, оставшуюся от « распада » , распространяющуюся в виде волн, причём с неизменяемой длиной волны, близкой ( равной ) волнам диапазона реликтового фона. Учитывая, что плотность энергии реликтового фона и , в сумме, ИК и оптического спектра совпадают ( ${displaystyle 10^{-14}}$ Дж ${displaystyle m^{-3}}$ ) с необходимостью следует вывод : радиочастотный фон является следствием «остывших» фотонов ИК и видимого оптического излучения.

При достижении порогового значения энергии обеспечивается постоянное пополнение энергией фонового излучения и поддержание уровня ( ${displaystyle 10^{-14}}$ Дж ${displaystyle m^{-3}}$ ), несмотря на многочисленные каналы потерь энергии радиоволн при взаимодействии с заряженными частицами и поглощению в объектах Вселенной.

К сему, численный пример. «Окно» микроволнового излучения 1 – 0.07 см. с максимумом в точке – 0.2 см., что соответствует частоте ${displaystyle 1.5*10^{11}c^{-1}}$ для максимума и ${displaystyle 0.5*10^{12}c^{-1}}$ для — 0.07 см.

Увеличение длины волны при распаде фотона оказывается по величине больше, чем при Доплер — эффекте. Например, для источника света с частотой ${displaystyle 10^{13}c^{-1}}$ на расстоянии светового года длина волны от начальной ${displaystyle 0.6*10^{-5}}$ увеличивается до ${displaystyle 0.5*10^{-4}}$ м, при уменьшении расстояния до половины светового года — от ${displaystyle 0.6*10^{-5}}$ до ${displaystyle 1.1*10^{-5}}$ м.

Для сравнения , красное смещение от Доплер – эффекта при удалении источника со скоростью равной четверти от скорости света для частоты ИК диапазона ${displaystyle 5.5*10^{13}c^{-1}}$ длина волны увеличивается с ${displaystyle 0.6*10^{-5}}$ до ${displaystyle 0.75*10^{-5}}$ м. Последнее значение при распаде достигается за время ${displaystyle 3*10^{9}}$ с.

Важным результатом является зависимость скорости распада фотона ${displaystyle vartheta ={frac {dE}{dt}}}$ от начальной энергии ${displaystyle hv_{0}:vartheta =-theta v_{0}e^{-hv_{0}theta ^{-}1}}$ , что очевидно и из зависимости ( 7 ) — угловой коэффициент ( по модулю ) уменьшается с ростом начальной энергии .

Гигантские времена жизни УФ, рентгеновских и – фотонов, при исследовании формулы ( 10 ) , исключают возможность участия этих излучений в формировании « пикового» по энергии интервала в области микроволнового фона, однако , при гипотетическом предположении полного распада этих фотонов до частоты ${displaystyle 10^{12}c^{-1}}$ , сохраняется логическая строгость выводов, основанных на формулах ( 7,10 ) — финал в распаде любого кванта завершается частотой радиоизлучения в области , так называемого , «реликтового» (?) фона с максимальной плотностью энергии в « окне » 0.01 – 3 см. , плотностью , превышающей остальной спектр частот в 25 — ${displaystyle 10^{-5}}$ раз.

На вопрос : “ Почему энергия не распределена равномерно по всему спектру частот ? “ возможен только один ответ : “ Явление распада фотонов перемещает энергию всех источников излучений в интервал частот близких ${displaystyle 10^{12}c^{-1}}$ при достижении предельного уровня энергии для фотонов ${displaystyle 10^{-22}}$ Дж

Что же касается “ горячего Б.В. “ , подтверждением которого является расширение Вселенной, установленное по красному смещению на основе Доплер – эффекта , то с учетом увеличения длин волн при распаде фотона “расширение” несколько замедляется … Образовавшийся фон микроволнового излучения при Б.В. , существует 13 млр. лет…вопреки закону сохранения энергии .

Заключение[править]

На основе вариационного принципа в координатах E-t получено уравнение зависимости фотона от времени. Исследование этого уравнения позволило:

— открыть явление перекачки энергии фотона в потенциальное поле.

— установить природу « реликтового» фона и однозначно указать источник и вычислить частоту микроволнового излучения.

— к известным каналам красного смещения добавить превалирующее явление сдвига волн по природе потери энергии движущимся фотоном,

— установить , что частота микроволнового фона совпадает с предсказанной частотой распада .

— показать важность больших времён жизни фотонов рентгеновского и гамма – излучений при расшифровке космических измерений ,

— сравнить значимость фундаментального эффекта Доплера и явления распада фотона: красное смещение космического излучения в основном обусловлено потерей энергии фотонов при движении в пространстве , формула ( 7 ) и ( 27)

— подвергнуть сомнению концепцию “ расширяющейся Вселенной “ , которая основана на явлении эффекта Доплера , оказывающего незначительный вклад по сравнению со свойством фотонов терять энергию в процессе своего движения в пространстве.

— установить границу f существования фотонов как частиц . Диапазону радиоизлучений , в котором никогда квантования не наблюдалось , соответствуют частоты ниже порога f .

Примечания и пояснения[править]

Оценка величины космической энергии[править]

на основе:

1) теории распада фотонов,

2) двух, следующих из этой теории, постулатов :

— Процесс распада фотона дискретный во времени и пространстве с интервалом, определённым как ${displaystyle {frac {h}{theta }}=10^{-12}}$ c.

— Величина энергии, теряемая фотоном на каждом акте распада в интервале времени ${displaystyle 10^{-12}}$ с , равна ${displaystyle 10^{-22}}$ Дж . Это значение также определяет минимальную энергию для существования фотона как частицы и соответствует максимуму области микроволнового фона.

Заметим — область микроволнового фона представляет “ накопитель” энергии, ранее распавшихся фотонов, чем и поддерживается постоянный уровень интенсивности микроволнового фона.

Итак, установлено, что при распаде фотона происходит уменьшение энергии дискретным образом с излучением кванта энергии величиной при каждом акте распада, причём эта энергия , приводящая к уменьшению энергии “материнского” фотона последовательно до частот микроволнового диапазона, аккумулируется в энергию потенциальную – фотонов ансамбля распадающегося фотон и фотонов всей Вселенной. Кванты заполняют пространство потенциальной энергии, которая по современным представлениям, не востребована, хотя гипотетически , является тем “ материальным “ полем ( которое раньше называли “эфиром”), в котором формируется излучение фотона , его движение, распад, физические процессы столкновений, преломления и дифракции. В скобках (исследование этого потенциального поля откроет практические способы извлечения энергии , подобно тому, как например, в настоящее время используются явления света – оптика, голография и энергетического преобразования свет – электроэнергия.)

Величины потенциальной энергии фотонов порядка ${displaystyle 10^{19}}$ Дж в с постоянным пополнением — ${displaystyle 10^{8}}$ Дж в м3 в год. В пространстве нашей Галактики эта энергия достигает величины — ${displaystyle 10^{30}}$ Дж.

Подробно:

— предполагаем время жизни Вселенной – 10 млр. лет

— принимаем год — ${displaystyle 10^{10}}$ сек., общее время — ${displaystyle 10^{20}}$ сек.

— в каждый интервал времени ${displaystyle {frac {h}{theta }}=10^{-12}}$ c испускается энергия ${displaystyle theta =10^{-22}}$ Дж в поле потенциальной энергии фотонов, За время существования Вселенной произошло ${displaystyle 10^{32}}$ актов,

— Учитывая, что в м3 фотонов ${displaystyle 4*10^{8}}$ , то полная энергия — ${displaystyle 3*10^{19}}$ Дж.

Заметим, что эта энергия потенциальная и проявление этой энергии в гравитационных эффектах не существует, однако, её использование при определённых условиях возможно, подобно потенциальной энергии земного притяжения.

Строгости ради и в качестве заключения к дополнению подчеркнем: энергия первоначального фотона разделяется на два канала – загрузка микроволнового фона и поток квантов в потенциальное фотонное поле.

Связь потенциальной энергии с энергией нулевых колебаний — предмет дальнейших исследований.

Литература[править]

В.Г. Левич Курс теоретической физики. — изд. «Наука», 1971.

Я.И. Френкель Аналитическая механика. — изд. «Кубуч»., 1937.

В.К.Семенченко Избранные главы теоретической физики. — изд. «Просвещение», 1966.

С.А.Ломашевич Фотон. Уравнение и теория распада. — изд. ‘Культ Информ Пресс’, 2015.

А. Эйнштейн Об энтропии излучения. Собрание научных трудов. — изд. “ Наука “, 1966.

А. Эйнштейн Предельный закон для энтропии монохроматического излучения. — изд. “ Наука “, 1966.

На основании базовых положений статистической физики и принципа наименьшего действия вычислено уравнение распада фотона. Определена нижняя граница существования фотонов по энергии. Рассмотрен процесс уменьшения энергии фотона во времени. В статье представлена оригинальная точка зрения на гипотезу Расширяющейся Вселенной . По результатам математических вычислений следует возможность красного смещения в результате распада фотона — уменьшения его энергии во времени. Возникающее при этом явлении красное смещение волны оказывается конкурирующим со смещением при Доплер – эффекте. Определен порог по энергии для существования фотона в виде кванта до его преобразования в волну. Представлена теория формирования микроволнового фона без «реликтового» догматизма.

Автор[править]

С.А. Ломашевич

Источник

Formulas[edit]

Physics[edit]

Electronvolt[edit]

Examples[edit]

See also[edit]

References[edit]

Фотоны

Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.

Энергия фотона

Импульс фотона

Давление света

Двойственная природа света

Теория атома водорода по Бору

ВЫЧИСЛЕНИЕ УРАВНЕНИЯ РАСПАДА ФОТОНА[править]

Вычисление времени жизни фотона другим манером[править]

Энтропия и свободная энергия фотона. Определение кванта энергии при распаде.[править]

Определение связанной энергии при распаде[править]

Определение модуля распределения[править]

Астрофизический аспект исследований[править]

Потенциальная энергия фотонного поля[править]

Решение проблемы микроволнового фона. Гипотеза[править]

Заключение[править]

Примечания и пояснения[править]

Оценка величины космической энергии[править]

Литература[править]

Автор[править]

Не пропустите также: