Как найти минимальное значение произведения - AvtoShod.ru

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Поиск наибольшего/наименьшего значения у произведения

(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).

(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.

(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).

(blacktriangleright) Если функция задана как произведение двух других функций, то [{Large{(fcdot g)’=f’cdot g+fcdot g’}}]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]

Задание
1

#2824

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = 2x^2cdot e^{x} — 3).

1) [y’ = 4xcdot e^{x} + 2x^2cdot e^{x} = 2x(x + 2)cdot e^x]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x(x + 2)cdot e^x = 0qquadLeftrightarrowqquad x(x + 2) = 0,,] откуда находим корни (x_1 = -2), (x_2 = 0). Производная функции (y) существует при любом (x). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

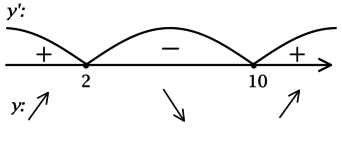
2) Найдём промежутки знакопостоянства (y’):

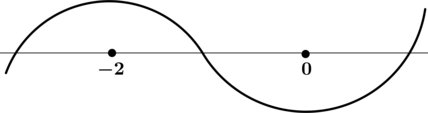
3) Эскиз графика (y):

По полученному эскизу нельзя сказать наверняка, действительно ли в точке локального минимума (x = 0) значение функции наименьшее, или же при каком-то отрицательном (x) значение функции окажется меньше, чем при (x = 0). Найдём (y(0)): [y(0) = 2cdot 0cdot e^{0} — 3 = -3,.] Рассмотрим произвольное (x_0 < 0), тогда [y(x_0) = 2{x_0}^2cdot e^{x_0} — 3,,] но ({x_0}^2geqslant 0) и (e^{x_0}geqslant 0), тогда [y(x_0) = 2{x_0}^2cdot e^{x_0} — 3geqslant 0 — 3geqslant -3,,] следовательно, наименьшее значение функции (y) равно (y(0) = -3).

Ответ: -3

Задание
2

#904

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = xcdot e^{x}cdot e — 11).

1) (y’ = e^{x}cdot e + xcdot e^{x}cdot e = (x + 1)cdot e^{x + 1}).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (x + 1)cdot e^{x + 1} = 0qquadLeftrightarrowqquad x = -1] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

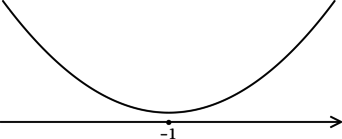
3) Эскиз графика (y):

Таким образом, (x = -1) – точка минимума функции (y).
(y(-1) = -1cdot e^0 — 11 = -12),

Итого: наименьшее значение функции (y) равно (-12).

Ответ: -12

Задание
3

#905

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = (2 — x)cdot e^{-x}cdot e^3 — 2).

1) (y’ = -e^{-x}cdot e^3 — (2 — x)cdot e^{-x}cdot e^3 = (x — 3)cdot e^{-x + 3}).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (x — 3)cdot e^{-x + 3} = 0qquadLeftrightarrowqquad x = 3] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

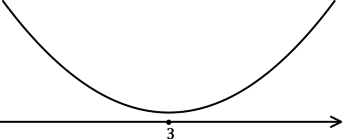
3) Эскиз графика (y):

Таким образом, (x = 3) – точка минимума функции (y).
(y(3) = -1cdot e^0 — 2 = -3),

Итого: наименьшее значение функции (y) равно (-3).

Ответ: -3

Задание
4

#909

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = (x^2 — 14x + 34)e^{x}) на отрезке ([0; 2,5]).

1) (y’ = (2x — 14)e^{x} + e^{x}(x^2 — 14x + 34) = e^{x}(x^2 — 12x + 20)).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad e^{x}(x^2 — 12x + 20) = 0qquadLeftrightarrowqquad x^2 — 12x + 20 = 0] (так как (e^x > 0) при любом (x) и на неё можно поделить), откуда находим корни (x_1 = 2, x_2 = 10). Таким образом, [y’ = e^{x}(x — 2)(x — 10).] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

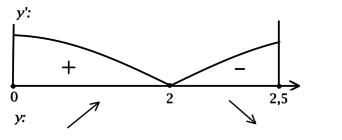
2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; 2,5]):

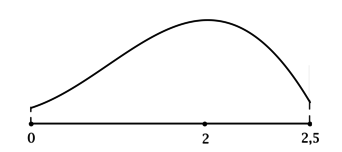
4) Эскиз графика на отрезке ([0; 2,5]):

Таким образом, (x = 2) – точка локального максимума функции (y) и наименьшее значение на ([0; 2,5]) функция достигает либо в (x = 0), либо в (x = 2,5). Сравним эти значения:

(y(0) = 34cdot e^0 = 34),

(y(2,5) = (6,25 — 35 + 34)e^{2,5} = 5,25cdot e^{2,5}). Так как (e > 2,7), то (5,25cdot e^{2,5} > 5,25cdot 2,7^{2,5} > 5,25cdot 2,7^{2} = 38,2725 > 34 = y(0)).

Итого: наименьшее значение функции (y) на ([0; 2,5]) равно (34).

Ответ: 34

Задание
5

#910

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = e^{-1}(x^2-8x+13)e^{x}) на ([-1; 5,5]).

Заметим, что (e^{-1}) – просто число, тогда

1) (y’ = e^{-1}((2x-8)e^{x}+e^{x}(x^2-8x+13)) = e^{-1}(x^2-6x+5)e^{x}).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad e^{-1}(x^2-6x+5)e^{x} = 0qquadLeftrightarrowqquad x^2-6x+5 = 0] (так как (e^x > 0) при любом (x) и на неё можно поделить), откуда находим корни (x_1 = 1, x_2 = 5). Таким образом, [y’ = e^{-1}(x — 1)(x — 5)e^{x}.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

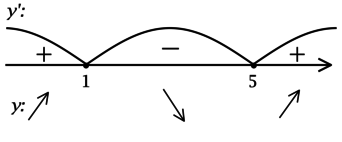
2) Найдём промежутки знакопостоянства (y’):

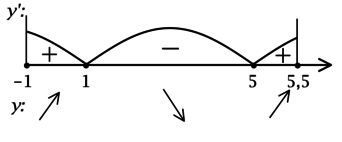
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-1; 5,5]):

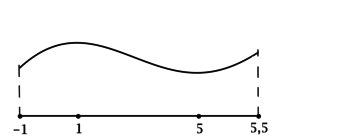
4) Эскиз графика на отрезке ([-1; 5,5]):

Таким образом, (x = 1) – точка локального максимума функции (y), (x = 5) — точка локального минимума функции и наибольшее значение на ([-1; 5,5]) функция достигает либо в (x = 1), либо в (x = 5,5). Сравним эти значения:

(y(1) = e^{-1}(1-8+13)e^{1} = 6cdot e^{-1 + 1} = 6cdot e^{0} = 6),

(y(5,5) = e^{-1}(30,25-44+13)e^{5,5} = -0,75cdot e^{-1 + 5,5} = -0,75cdot e^{4,5} < 0 < 6 = y(1)).

Итого: наибольшее значение функции (y) на ([-1; 5,5]) равно (6).

Ответ: 6

Задание
6

#907

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = (-2x + 1)cdot e^{-x}cdot e^{1,5}).

1) (y’ = -2e^{-x}cdot e^{1,5} — (-2x + 1)cdot e^{-x}cdot e^{1,5} = (2x — 3)cdot e^{-x + 1,5}).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (2x — 3)cdot e^{-x + 1,5} = 0qquadLeftrightarrowqquad x = 1,5] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

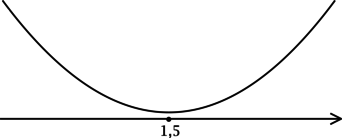
3) Эскиз графика (y):

Таким образом, (x = 1,5) – точка минимума функции (y).
(y(1,5) = -2cdot e^0 = -2),

Итого: наименьшее значение функции (y) равно (-2).

Ответ: -2

Задание
7

#906

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = (3x + 2)cdot e^{-x}cdot e^{frac{1}{3}}).

1) (y’ = 3e^{-x}cdot e^{frac{1}{3}} — (3x + 2)cdot e^{-x}cdot e^{frac{1}{3}} = (-3x + 1)cdot e^{-x + frac{1}{3}}).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (-3x + 1)cdot e^{-x + frac{1}{3}} = 0qquadLeftrightarrowqquad x = dfrac{1}{3}] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

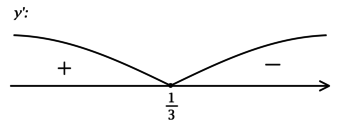
2) Найдём промежутки знакопостоянства (y’):

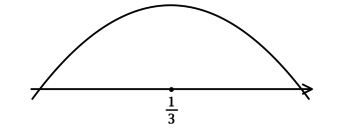
3) Эскиз графика (y):

Таким образом, (x = dfrac{1}{3}) – точка максимума функции (y).
(yleft(dfrac{1}{3}right) = 3cdot e^0 = 3),

Итого: наибольшее значение функции (y) равно (3).

Ответ: 3

УСТАЛ? Просто отдохни

Источник

$begingroup$

Let $a$ and $b$ two integers
Such that (a+b) is solution to the equation $x^2+ax+b=0$ .
Find the minimal value of the product $ab$.

• Please help i’m really stuck on this , i cannot find any good bounds . This problem appeared in a morroccan national olympiad.

Bill Dubuque

265k37 gold badges278 silver badges906 bronze badges

asked Oct 17, 2020 at 22:30

$endgroup$

$begingroup$

You have $$(a+b)^2+a(a+b)+b=0\
2a^2+3ab+b^2+b=0\
a=frac{-3bpmsqrt{(b-4)^2-16}}4$$

Note that $bge 8$ or $ble 0$. If $bge 8$ then the only possible values of $b$ are $8$ and $9$ (otherwise $(b-4)^2-16$ is not a square). If $b=8$ then $a=-6$, $ab=-48$. If $b=9$ then $a=frac{-27pm 3}4$, so $a=-6$, $ab=-54$

If $ble 0$ then the only possible values of $b$ are $0,-1$. If $b=0,a=0$ and $ab=0$. If $b=-1, a=(3pm 3)/4$, so $b=-1, a=0$, $ab=0$.

Thus the smallest value of $ab$ is $-54$.

answered Oct 17, 2020 at 23:06

markvsmarkvs

19.5k2 gold badges17 silver badges34 bronze badges

$endgroup$

$begingroup$

Similar to Mark Sapir’s answer, but slightly simpler, write $(a+b)^2+a(a+b)+b=0$ as a quadratic in $b$ (instead of $a$), that is $b^2+(3a+1)b+2a^2=0$, and solve to

$$b={-(3a+1)pmsqrt{(3a+1)^2-8a^2}over2}={-(3a+1)pmsqrt{a^2+6a+1}over2}={-(3a+1)pmsqrt{(a+3)^2-8}over2}$$

In order for $b$ to be an integer, we must have $(a+3)^2=9$, so $a=0$ or $-6$. The case $a=0$ gives $ab=0$, while the case $a=-6$ gives $b=(17pm1)/2$, i.e, $9$ or $8$. The smallest value is $ab=-6cdot9=-54$.

answered Oct 18, 2020 at 0:40

Barry CipraBarry Cipra

79k8 gold badges75 silver badges154 bronze badges

$endgroup$

$begingroup$

So ve have to solve $$2a^2+3ab+b^2+b=0$$ in integers. Let $d=gcd(a,b)$ and $x,y$ such that $a=dx$ and $b=dy$, then $x,y$ are relatively prime and we have $$d(2x^2+3xy+y^2)=-y$$ so $y=dz$ for some integer $z$ and now we have $$2x^2+3dxz+d^2z^2 =-zimplies zmid 2x^2implies zmid 2$$ since $x,z$ are relatively prime. So we have 4 posible values for $z$, I will start only one, the rest are simillary.

$z=2$ then $x^2+3dx+2d^2=-1$ so $(x+2d)(x+d)=-1$ so …

answered Dec 25, 2020 at 21:11

nonusernonuser

88.4k19 gold badges101 silver badges195 bronze badges

$endgroup$

You must log in to answer this question.

Not the answer you’re looking for? Browse other questions tagged

.

Источник

Пусть $%a,b,c$% — натуральные числа, причем числа $%a cdot b, b cdot c, c cdot a$% делятся соответственно на числа $%3c, 11a, 61b$%. Найдите наименьшее возможное значение произведения $%abc$%.

Я решал следующим образом: из условия задачи следует, что $% frac{ab}{3c}=n; frac{bc}{11a}=m; frac{ca}{61b}=k$%, где $%n; m; k$% — натуральные числа. Перемножим эти выражения и получим $%nmk= frac{abc}{3 cdot11 cdot61 }$%. Тогда $%abc= 2013 cdot mnk $%. Минимальное значение произведения $%abc$% будет равно $%2013$%, при $%n=m=k=1$%. Я правильно рассуждал, или где-то ошибся. Заранее благодарен.

Источник

(%i5)   array(T,5,5);
(%o5)   T
(%i6)   for i:1 thru 5 do 
    for j:1 thru 5 do (T[i,j]: random (99)+1);
(%o6)   done
(%i7)   for i:1 thru 5 do (s:makelist(T[i,j],j,1,5), print (s));
[15,35,85,35,51]" "
[40,34,14,24,46]" "
[74,86,96,35,82]" "
[76,49,93,22,6]" "
[97,49,2,20,78]" "
(%o7)   done
(%i8)   block([s:[],i,j], 
        for i:1 thru 5 do
        for j:1 thru 5 do 
        (
            if evenp(j)=true then 
        (push(T[i,j],s))
            ),
            return(s)
    );
(%o8)   [20,49,22,49,35,86,24,34,35,35]

Источник

Задача взята с acmp.ru (Время: 1 сек. Память: 16 Мб Сложность: 42%)

Задача на внимательность.

Требуется найти наименьшее натуральное число Q такое, что произведение его цифр равно заданному числу N.

Входные данные:
В единственной строке входного файла INPUT.TXT записано одно целое число N (0 ≤ N ≤ 10^9).

Выходные данные:
В выходной файл OUTPUT.TXT нужно вывести искомое число Q. В том случае, если такого числа не существует, следует вывести -1.

Пример 1:
INPUT.TXT: 10
OUTPUT.TXT : 25

Пример 2:
INPUT.TXT: 13
OUTPUT.TXT : -1

Пример 3:
INPUT.TXT: 90
OUTPUT.TXT : 259

Итак, от нас требуют найти минимальное число, произведение цифр которого равно заданному значению. Первая мысль, которая может возникнуть — перебирать числа в порядке возрастания, делить их на цифры и перемножать. Однако, с учетом допустимых диапазонов входных данных — работать это будет слишком долго.

На самом деле, в задаче есть смысл стараться подобрать делители числа N. Можно заметить, что если число делится на 8 — то его делителями будут также 2 и 4, однако, 2 разряда дадут однозначно большее число, чем один (8 < 24). Поэтому по возможности надо выбирать как можно большие цифры. Тогда логика решения заключается в том, чтобы делить число на 9 пока делится нацело и считать число девяток, потом на 8 и т.д. Если в результате такой операции получается единица — вывод осуществляется в обратном порядке (от двойки к девятке выводится количество цифр). Если же единицу получить не удалось — выводим -1 (искомого Q не существует).

Дальше остается только учесть все детали. Первое — допустимым значением является ноль, но для такого значения наш алгоритм зациклится — его необходимо обработать отдельно. Кроме того, минимальным натуральным числом, таким, что произведение его цифр равно нулю является 10 (вычислить такое значение никак не получилось бы без перебора).

Другая проблема — если исходное число равно единице. По описанному выше алгоритму мы продолжаем делить число на цифры пока не получим единицу, но если мы получили ее сразу — то у нас нет ни одной цифры и в файл мы ничего не выведем. Поэтому такой случай также стоит обработать отдельно. Итак, финальный исходный код программы мог бы выглядеть следующим образом:

#include <fstream>
#include <algorithm>
using namespace std;

int main() {
  ifstream ifst("input.txt");
  ofstream ofst("output.txt");
  
  long long n;
  unsigned long long digits[10];
  ifst >> n;
  
  if (0 == n) {
    ofst << 10;
    return 0;
  }
  
  if (1 == n) {
    ofst << 1;
    return 0;
  }

  for (int i = 9; i > 1; --i) {
    digits[i] = 0;
    while (n%i == 0) {
      n/=i;
      digits[i]++;
    }
  }

  if (n == 1) {
    for (int i = 2; i <= 9; ++i) {
      while (digits[i]) {
        digits[i]--;
        ofst << i;
      }
    }
  }
  else {
    ofst << -1;
  }
}

Источник

Поиск наибольшего/наименьшего значения у произведения

You must log in to answer this question.

Not the answer you’re looking for? Browse other questions tagged .

Не пропустите также:

Not the answer you’re looking for? Browse other questions tagged

.