В статье собраны разные задачи: и на равноускоренное движение, и на движение с постоянной скоростью. Все задачи предназначаются для подготовки к олимпиадам.
Задача 1.
Определите минимальное время движения автобуса от одной остановки до другой, если расстояние между остановками
м. При движении автобуса от остановки он может развивать ускорение
м/c
, а при подходе к остановке тормозить с ускорением
м/c
. Ответ дать в секундах.
Решение.
Построим график зависимости скорости автобуса от времени.
Задача 1
Из условия минимальности времени следует, что автобус сначала непрерывно разгоняется с максимальным ускорением до максимальной скорости , а потом тормозит. Следовательно, график представляет собой треугольник с основанием
и высотой
. Откуда можно записать
, Вместе с тем,
и
, где
.
Подставляя всё в последнее уравнение, получим
Но
Или
Умножим на правую и левую части (1):
Заменим на
:
Тогда
Ответ: 30 с.
Задача 2.
Автомобили следуют друг за другом со скоростью км/ч. Внезапно первый начинает экстренно тормозить. Время реакции второго водителя примерно
секунды. При каком минимальном расстоянии между автомобилями столкновения не произойдет? Ускорения считать одинаковыми. Ответ выразить в метрах, округлив до целых.
Решение.
Самое простое решение — графическое. Построим на одних осях графики зависимости скорости машин от времени (на рисунке скорость первой машины показана красным, а второй — зеленым). Расстояние между машинами должно быть равно разности площадей под графиками, а это — площадь параллелограмма: м.
Задача 2.
Ответ: 6 м.
Задача 3. Тело движется по оси . По графику зависимости проекции скорости тела
от времени
определите, какой путь прошло тело за время от
до
с. Ответ выразите в метрах, округлив до целых.
Задача 3.
Решение. По площади под графиком определим расстояние, пройденное телом до разворота за первые 4 секунды движения и получим, что оно прошло 20 метров. За следующие 4 секунды тело прошло ещё 10 метров, причём из графика видно, что проекция скорости тела на ось поменяла знак, то есть тело развернулось и поехало в обратную сторону. Так как нас спрашивают путь, а не модуль перемещения, то найденные расстояния надо сложить. Окончательно, пройденный путь за 8 секунд равен 30 м.
Ответ: 30 м.
Задача 4.
На длинном шоссе на расстоянии 1 км друг от друга установлены светофоры. Красный сигнал каждого светофора горит в течение 30 с, зелёный в течение следующих 30 с. При этом все автомобили, движущиеся со скоростью 40 км/ч, проехав один из светофоров на зеленый свет, проезжают без остановки, то есть тоже на зеленый свет, и все остальные светофоры. С какой другой большей скоростью могут двигаться автомобили, чтобы проехав один светофор на зеленый свет, далее нигде не останавливаться?
Решение.
Самое простое решение — графическое. Нарисуем график движения автомобиля. По горизонтальной оси будем откладывать время в секундах, по вертикальной
— пройденный путь
в километрах. Изобразим на этом графике запрещающие сигналы каждого из светофоров
— красные
— в виде тёмных полосок, а разрешающие
— зелёные
— в виде светлых промежутков между ними. Тогда график движения любого автомобиля, движущегося без остановок, должен проходить только через светлые промежутки.
Задача 4.
Заметим, что расстояние 1 км между соседними светофорами автомобиль, движущийся со скоростью 40 км/ч, проедет за 1/40 часа = 90 секунд. Таким образом, он сможет проехать следующий светофор без остановки, только если разрешающие и запрещающие сигналы светофоров будут гореть в противофазе в каждой следующей цепочке (когда на первом перекрестке зеленый, на втором — красный). Из графика видно, что автомобиль будет двигаться без остановок на светофорах в том случае, если он будет преодолевать 1 км за 30 с, 90 с, 150 с,…, (30 + 60n) с, где n =0,1,2,… Следовательно, скорость автомобиля, требующаяся для движения по шоссе без остановок на светофорах, может быть равна 120 км/ч, 40 км/ч, 24 км/ч и т.д. Но, по условию нам нужно найти скорость большую, чем 40 км/ч. Окончательно, выбираем 120 км/ч.
Ответ: 120 км/ч.
Задача 5. Определите минимальное время движения автобуса от одной остановки до другой, если расстояние между остановками м. При движении автобуса от остановки он может развивать ускорение
м/c
, а при подходе к остановке тормозить с ускорением
м/c
. По правилам дорожного движения скорость автобуса на этом участке не должна превышать
м/с. Ответ дать в секундах, округлив до десятых.
Решение.
Если автобус будет только разгоняться и тормозить, то превысит ли его скорость допустимое значение? Построим график зависимости скорости автобуса от времени. Из условия минимальности времени следует, что надо успеть набрать максимальную скорость , следовательно, график представляет собой треугольник с основанием
и высотой
. Так как путь, который проходит автобус, численно равен площади под графиком зависимости скорости от времени, то
.
Вместе с тем, и
, где
.
Решая систему из трех полученных уравнений, получаем
Ускорение при разгоне меньше ускорения при торможении в два раза. Следовательно, разгон занял 40 с и скорость достигла 20 м/с, что больше допустимой. Это означает, что часть пути автобус двигался с постоянной максимально допустимой скоростью. Все движение можно разбить на три участка: разгон до , движение с постоянной скоростью и торможение до остановки.
На первом и третьем участке автобус двигался время и
и прошел расстояние
за с.
Оставшееся расстояние автобус шел с максимальной скоростью в течение времени
Общее время движения 127,5 с.
Ответ: 127,5 с.
2 комментария
Анна
✉️
31.08.2020 18:21:55
Здравствуйте меня интересует одна задача из этой темы
Две Вагонетки С начальной скоростью V идут по рельсам идёт снег. на одном из них спит человек с массой m а на другом такой же челоек с метлой убирает снег с вагонетки кто из них пройдет большее растояние
Анна Валерьевна
✨
01.09.2020 09:50:04
[latexpage] Скорость тележки с работающим дворником будет меняться при падении на нее снега следующим образом: при падении порции снега $Delta m$ скорость изменится в $frac{M}{M+Delta m}$ раз. Скорость будет меняться таким образом при падении каждой новой порции массой $Delta m$, и если их упадет $n$ штук, скорость изменится в $left(frac{M}{M+Delta m}right)^n$ раз.
Скорость тележки, на которой снег накапливается, растет в
$frac{M}{M+nDelta m}$ раз.
Показательная функция растет быстрее линейной, поэтому скорость тележки с работающим дворником будет быстрее уменьшаться. Дальше проедет тележка со спящим мужичком.

где:
- Скорость (V) — расстояние, пройденное за единицу времени.
- Время (t) — время в пути.
- Расстояние (S) — пройденный путь, или расстояние.
Зная эту формулу (для расстояния), вы можете легко вывести из неё формулу для скорости, или времени.
Если вы запомните эту формулу, то сможете решить любую задачу на движение, так как все задачи на движение по прямой — это применение данной формулы к одному или нескольким взаимосвязанным объектам.
Рассмотрим, как решать разные задачи на движение в зависимости от условий и уровня сложности.
Все задачи на движение делятся на следующие типы:
- простые задачи на скорость, время и расстояние;
- задачи на движение в разных направлениях: сближение и удаление;
- задачи на движение в одном направлении: сближение и удаление;
- решение задач на движение по реке.
Решение простых задач на движение: скорость, время и расстояние
В простых задачах на движение, как правило, есть один движущийся объект, для которого нужно найти неизвестную величину: скорость, время или расстояние. В данном случае применяется формула в ее первоначальном виде:
Задача 1. Автомобиль ехал 2ч со скоростью 85 км/ч. Определите расстояние.
Решение: Вычислим путь по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.
Задача 2. Велосипедист проехал 60 км за 5ч. Определите скорость.
Решение: Вычислим скорость велосипедиста по формуле: V = S:t = 60 км : 5 ч = 12 км/ч.
Задача 3. Мотоциклист проехал 30 км со скоростью 15км/ч. Сколько времени он затратил на этот путь?
Решение: Вычислим время движения мотоциклиста по формуле: t = S:V = 30 км : 15 км/ч = 2 ч.
В таких задачах нужно также следить, чтобы были одинаковыми единицы измерения. Например, если расстояние измеряется в километрах, а время — в часах, то скорость буде измеряться в км/час. Но если единицы измерения скорости — метр/час, а время дано в минутах, то в этом случае скорость и время нужно привести к одинаковым единица измерения, иначе ответ будет неверным.
Задача 4. Мотоциклист ехал 30 минут со скоростью 60 км/ч. Какое расстояние он проехал?
Решение: для того, чтобы вычислить расстояние, нужно время и скорость привести к одинаковым единицам измерения. При этом есть 2 способа:
1) Переведем время: 30 минут = 30/60 = 0,5 часа.
Найдем расстояние: 60 км/ч * 0,5 ч = 30 км.
2) Переведем скорость: 60 км/ч = 60км / 1час = 60км / 60 мин = 1км/мин.
Найдем расстояние: 1км/мин*30минут = 30 км.
Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)
При встречном движении расстояние между объектами уменьшается. Объекты приближаются друг к другу со скоростью сближения.
Скорость сближения находится по формуле:
При движении в противоположных направлениях скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью удаления.
Скорость удаления находится по формуле:
При решении подобных задач лучше нарисовать схему движения, чтобы было легче решать.
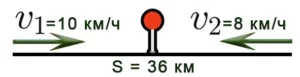
Задача 5. Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого велосипедиста 10 км/ч, второго — 8 км/ч. Через сколько часов они встретятся?
Решение: 1) Найдем скорость сближения: V=10+8 = 18 км/ч.
2) Найдем время: t = S:V = 36 : 18 = 2 ч.
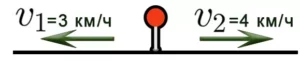
Задача 6. Два пешехода вышли одновременно из одного и того же пункта в противоположных направлениях. Скорость первого пешехода 3км/ч, второго — 4км/ч. Какое расстояние между ними будет через 30 минут?
Решение: 1) Найдем скорость удаления пешеходов: V = 3+4=7 км/час.
2) Переведем в соответствие единицы измерения: t=30 мин = 0,5 ч.
3) Найдем расстояние: S=V × t = 7 × 0,5 = 3,5 км.
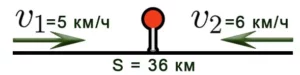
Задача 7. Два автобуса выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 300 км. Через 2 часа они встретились. Найдите второго второго автобуса, если первый ехал со скоростью 70 км/ч.
Решение. 1) Нам известно расстояние и скорость, поэтому найдем скорость по формуле: V = S:t = 300:2=150км/ч. Это скорость сближения.
2) Найдем скорость второго автобуса: 150-70 = 80км/ч.
Решение задач на движение в одном направлении: сближение и удаление
Если два объекта движутся в одном направлении и один объект “догоняет” второй, то расстояние между объектами уменьшается.
Скорость сближения при таком движении определяют по формуле:
Если два объекта движутся в одном направлении и один объект “отстает” от второго, то расстояние между объектами увеличивается.
Скорость удаления при таком движении определяют по формуле:
Если объект движется в стоячей воде (озере), то его скорость называют собственной скоростью объекта. То есть, скорость объекта равная собственной скорости объекта.
Заметим, что плот — это тело, у которого собственная скорость равна нулю (V=0). Значит, плот может плыть только по течению и со скоростью течения.
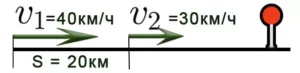
Задача 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль едет со скоростью 40км/ч, второй — со скоростью 30км/ч. Через сколько часов первый автомобиль догонит второй?
Решение. 1) Найдем скорость сближения автомобилей: V=40-30=10км/ч.
2) Зная расстояние (20км) и скорость сближения (10км/ч) найдем время: 20:10=2 часа.
Задача 9. Из одного населенного пункта выехали автомобиль и автобус. скорость автомобиля 70 км/ч, скорость автобуса — 50 км/ч. Какое расстояние будет между ними через 3 часа?
Решение. 1) Найдем скорость удаления : V=70-50=20км/ч.
2) Зная скорость удаления и время, найдем расстояние: S = 20*3 =60 км.
Решение задач на движение по реке
Особенностью задач на движение реке является то, что у объекта появляется дополнительная скорость — скорость течения реки. При этом возможно два варианта:
- по течению реки → скорость увеличивается;
- против течения реки → скорость уменьшается.
Таким образом, в задачах рассматривают 2 скорости:
- Скорость собственная — Vs;
- Скорость течения реки — Vt.
Задача 9. Собственная скорость лодки составляет 12 км/ч. Скорость течения реки равна 3 км/ч. Какое расстояние проплывёт лодка через 3 часа, если она плывёт по течению реки?
Решение. 1) Найдем скорость лодки. Так как она плывет по течению реки, ее скорость увеличивается.
V = Vs+ Vt = 12+3 =15км/ч.
2) Найдем расстояние: S=V×t = 15×3=45км.
Задача 10. Собственная скорость катера составляет 30 км/ч. Скорость течения реки равна 4 км/ч. Какое расстояние преодолеет катер через 4 часа, если он плывёт против течения реки?
Решение. 1) Найдем скорость. Так как катер плывет против течения реки, его скорость уменьшится.
V = Vs- Vt = 30-4 =26 км/ч.
2) Найдем расстояние: S=V×t = 26 * 4 = 104 км.
Задача 10. Скорость лодки равна 10 км/ч. При этом надо успеть проплыть 25 км за 2 часа по течению реки. Какой должна быть скорость течения реки, чтобы успеть в срок?
Решение. 1) Найдем нужную скорость: V=S:t = 25:2=12,5 км/ч.
2) Найдем скорость, которую нужно прибавить до нужно (скорость течения реки): 12,5-10=2,5км/ч.
Задача 11. Уровень ЕГЭ.
Катер прошёл по течению реки 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения.
Решение: Пусть Vt — cкорость течения реки, тогда:
1) В одну сторону: 27+Vt – скорость перемещения катера по течению, S=120км.
2) В обратную сторону: 27-Vt – скорость перемещения катера против течения, S=120км.
Выразим время:
1) В одну сторону: t=S:V = 120:(27+Vt) – время, затраченное катером на перемещение по течению,
2) В обратную сторону: t=S:V = 120:(27-Vt) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то:
120:(27+Vt) +1 = 120:(27-Vt).
Далее решаем уравнение и получаем ответ 3 км/ч.
Больше задач на движение Ваш ребёнок может решить, скачав программы:
Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.
Полезные советы для решения задач на движения
- В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
- Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.
- При решении задач на движение рисуйте картинки. Особенно, когда текст задачи большой и сразу в голове не укладывается. Чаще всего это нужно делать в задачах, где кто-то кого-то догоняет, встречается, или перемещается между пунктами А и В туда и обратно. На картинке сразу видно, какие отрезки пути можно просчитать. Картинка облегчает составление математической модели.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
Переправы.
Рассмотрите решение задач.
Задача 1. Минимальное время, которое необходимо, чтобы переплыть в лодке реку, равно $t_0$. Ширина русла реки равна $H$. Скорость течения реки постоянна в любом месте русла и в $beta$ раз больше скорости лодки ($beta > 1$), плывущей в стоячей воде.
1. Найдите скорость лодки в стоячей воде.
2. На какое расстояние снесет лодку за минимальное время переправы?
3. Определите наименьшее расстояние, на которое может снести лодку за время переправы.
4. Найдите время переправы лодки в том случае, когда ее сносит на минимальное расстояние.
Решение.
1. Минимальное расстояние между берегами – это ширина реки. Если направить лодку перпендикулярно берегу, то время ее движения будет минимальным
$t_0 = frac{H}{v_Л}$,
так как $H$ – минимально, а $v_Л$ – максимальна, тогда
$v_Л = frac{H}{t_0}$. (1)
2. Так как вектор скорости лодки направлен перпендикулярно берегу, то снос лодки зависит только от скорости течения. Скорость течения реки
$v_T = beta v_Л$
за время переправы лодку снесет на расстояние
$L = v_T cdot t_0 = beta v_Л cdot t_0 = beta H frac{t_0}{t_0} = beta H$
Снос лодки (за минимальное время движения) составит
$L = beta H$ (2)
3. Снос лодки во время переправы будет зависеть от двух факторов: скорости лодки в направлении течения и скорости лодки в направлении перпендикулярном берегу. Необходимо определиться с углом вектора скорости лодки. Относительно простым способом нахождения угла является графический метод. Скорость лодки относительно системы координат, связанной с берегом, равна векторной сумме скоростей течения и лодки (рис. 6.1). Из рисунка видно, что минимальное расстояние $L_{min}$ сноса лодки соответствует случаю, когда относительная скорость лодки направлена по касательной к окружности радиуса $v_Л$. Из подобия треугольников скоростей и расстояний, имеющих общий угол $alpha$, получим
$frac{L_{min}}{H} = frac{v}{v_Л}$,
и так как $v perp v_0$, находим
$L_{min} = Hfrac{v}{v_Л} = H frac{sqrt{v_T^2 – v_Л^2}}{v_Л} = Hfrac{sqrt{beta^2 frac{H^2}{t_0^2} − frac{H^2}{t_0^2}}}{H/t_0} = H sqrt{beta^2 − 1}$. (3)
4. Время переправы лодки, когда ее сносит на минимальное расстояние, зависит от проекции скорости лодки на ось $Oy$.
Проекция скорости лодки на $Oy$ равна
$v_y = v_Л cdot cosalpha$
С другой стороны
$cosalpha = frac{L_{min}}{sqrt{L_{min}^2 + H^2}} = frac{Hsqrt{beta^2 − 1}}{sqrt{H^2 (beta^2 − 1) + H^2}} = frac{sqrt{beta^2 − 1}}{beta}$.
Время переправы в этом случае
$t = frac{H beta}{v_Л sqrt{beta^2 − 1}} = frac{beta t_0}{sqrt{beta ^2 − 1}}$. (4)
Замечание 1. Минимальное время переправы лодки через руку будет в случае движения лодки перпендикулярной берегу.
Замечание 2. Минимальный снос лодки будет в случае, когда вектор скорости лодки будет перпендикулярен вектору относительной скорости лодки.
Замечание 3. Определение угла между вектором скорости лодки и (например) вертикалью, для минимального сноса при переправе через реку возможно следующими способами:
Через исследование функции. При переправе на другой берег
$H = v_Л cosalpha cdot t$ и $L = (v_T – v_Л sinalpha) cdot t$.
Составим уравнение траектории $L(H)$
$L = (v_T – v_Л sinalpha)frac{H}{v_Л cosalpha} = v_T frac{H}{v_Л cosalpha} – Htgalpha$.
Окончательно,
$L = v_T frac{H}{v_Л cosalpha} – H cdot tgalpha$.
Продифференцировав последнее уравнение по углу $alpha$ и, приравняв к нулю производную, найдем, при каких значениях угла $alpha$ расстояние $L$ будет минимальным.
$(frac{v_T H}{v_Л cosalpha} – Htgalpha)^/ = frac{v_T H sinalpha}{v_Л cos^2 alpha} − frac{H}{cos^2 alpha} = 0$,
$sinalpha = frac{v_Л}{v_T} = frac{1}{beta}$.
Через тригонометрическую единицу
$sin^2 alpha + cos^2 alpha = 1$,
Найдем
$cos alpha = frac{sqrt{beta^2 − 1}}{beta}$.
Методом дискриминанта.
Уравнение траектории перепишем в виде
$L = v_T frac{H}{v_Л cosalpha} – frac{Hsinalpha}{cosalpha}$
или
$Lcosalpha = beta H – Hsinalpha$.
Возведем уравнение в квадрат
$L^2 cos^2 alpha = beta^2 H^2 + H^2 sin^2 alpha – 2beta H^2 sinalpha$.
Воспользовавшись тригонометрической единицей
$sin^2alpha + cos^2alpha = 1$
Тогда
$L^2 (1 – sin^2alpha) = beta^2 H^2 + H^2 sin^2 alpha – 2beta H^2 sinalpha$
Мы получили квадратное уравнение относительно искомого угла $alpha$. Преобразуем его к «нормальному» (удобному виду).
$(L^2 + H^2) sin^2 alpha – 2beta H^2 sinalpha − (L^2 − (beta H)^2) = 0$.
Решение квадратного уравнения имеет вид:
$sinalpha_{1,2} = frac{beta H^2 pm sqrt{(beta H^2)^2) – (beta^2 H^2 – L^2)(L^2 + H^2)}}{L^2 + H^2}$.
При этом $D geq 0$:
$beta^2 H^4 – (beta^2 H^2 – L^2)(L^2 + H^2) = L^2 (L^2 − beta^2 H^2 + H^2) geq 0$.
При уменьшении $L$ уменьшается дискриминант. Минимальное значение $D = 0$. Тогда,
$L^2 = beta^2 H^2 – H^2$, и $L = H sqrt{beta^2 − 1}$,
что соответствует минимальному сносу.
Из рисунка видно, что
$cosalpha = frac{L_{min}}{sqrt{L_{min}^2 + H^2}} = frac{Hsqrt{beta^2 − 1}}{sqrt{H^2 (beta^2 − 1) + H^2}} = frac{sqrt{beta^2 − 1}}{beta}$.
Замечание 4. Если скорость течения меньше скорости лодки, то минимальный снос возможен только при движении лодки за минимальное время (см. решение 1).
Задачи для самостоятельного решения.
1. Катер, переправляясь через реку шириной $800$ м, двигался со скоростью $4$ м/с так, что время его переправы оказалось минимальным. На сколько будет снесен катер течением, если скорость течения реки равна $1,5$ м/с?
2. При переправе через реку шириной $60$ м надо попасть в точку, лежащую на $80$ м ниже по течению, чем точка старта. Лодочник управляет моторной лодкой так, что она движется точно к цели со скоростью $8$ м/с относительно берега. Какова при этом скорость лодки относительно воды, если скорость течения реки $2,8$ м/с?
3. Под каким углом к берегу должна идти моторная лодка, чтобы пересечь реку шириной $300$ м за минимальное время, если скорость лодки относительно воды $18$ км/ч, а скорость течения $2$ м/с? На сколько при этом сместится лодка вдоль берега?
4. На лодке переплывают реку, отправляясь из пункта $A$. Скорость лодки в стоячей воде $5$ м/с, скорость течения реки $3$ м/с, ширина реки $200$ м. а) В какой точке лодка пристанет к противоположному берегу, если держать курс перпендикулярно берегам? б) Какой курс следует держать, чтобы попасть в точку $B$, находящуюся на противоположном берегу напротив точки $A$? Для обоих случаев найдите время переправы.
5. Пловец хочет переплыть реку шириной $h$. Под каким углом $alpha$ к направлению течения реки он должен плыть, чтобы переправиться за наименьшее время? Какой путь он проплывет? Скорость течения реки $u$, скорость пловца относительно воды $v$. За какое время он переплывет реку по наикратчайшему пути?
6. Два катера вышли одновременно из пунктов $A$ и $B$ находящихся на разных берегах, причем пункт $B$ ниже по течению. Оба катера движутся по прямой $AB$, длина которой равна $l = 1$ км. Прямая $AB$ образует угол $alpha = 60^0$ с направлением скорости течения, которая равна $v = 2$ м/с. Катера встретились через $3$ мин после отхода от причалов. На каком расстоянии от пункта B произошла встреча?
7. Турист, сплавлявшийся на байдарке по реке, заметил, что поток несет его к середине упавшего и перегородившего ему путь дерева в тот момент, когда расстояние от носа байдарки до дерева было $S = 30$ м. Оценить, под каким углом к скорости течения он должен направить байдарку, чтобы обойти преграду. Скорость течения реки $u = 3$ км/ч, скорость байдарки относительно воды $6$ км/ч, длина дерева $l = 20$ м.
8. Скорость течения реки $5$ м/с, ее ширина $32$ м. Переправляясь через реку на лодке, скорость которой относительно воды $4$ м/с, рулевой обеспечил наименьший возможный снос лодки течением. Чему равен этот снос?
9. Из пункта $A$, расположенного на берегу реки, необходимо попасть в пункт в пункт $B$, находящийся на противоположном берегу, выше по течению на расстоянии $2$ км от перпендикуляра, проведенного из точки $A$ к противоположному берегу. Ширина реки $1$ км, максимальная скорость лодки относительно воды $5$ км/ч, а скорость течения реки $2$ км/ч. Сможет ли лодка переплыть за $30$ мин на другой берег, двигаясь по прямой $AB$.
10. Две моторные лодки, расположенные друг против друга на противоположных берегах прямолинейного участка шириной $H = 200$ м, совершают переправу так, что время переправы одной лодки и перемещение другой лодки за время ее переправы минимальны. Скорость $v = 5$ м/с каждой лодки относительно воды в $n = 2$ раза больше скорости течения. Найти минимальное расстояние между лодками и время $T$ их движения для сближения на это расстояние, если лодки начинают переправу одновременно. Скорость течения и скорость движения каждой лодки в течение переправы считать постоянными.
Если заметили неточность, ошибку, есть замечания, предложения, то пишите сюда
Время, скорость, расстояние
О чем эта статья:
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x ( t ) = x 0 + v 0 t + a t 2 2 . .
Теперь мы можем выделить кинематические характеристики движения тела:
Перемещение тела определяется формулой:
s = v 0 t + a t 2 2 . .
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2
Кинетическая энергия тела определяется формулой:
Скорость при прямолинейном равноускоренном движении равна:
v = v 0 + a t = 5 − 6 t
Поэтому кинетическая энергия тела равна:
E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2
Следовательно, правильная последовательность цифр в ответе будет: 34.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Примеры решения задач
Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)

1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчета – 10 м;
- начальная скорость 20 м/с;
- постоянное касательное ускорение at/2 = 5 м/с ; at= — 10 м/с .
- ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.
Решение
1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).
Нормальное ускорение (ап = v 2 /r) при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.
2. На участке ВС:
— касательное ускорение равно нулю: at = 0;
— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.
3. На участке CD полное ускорение равно нулю.
Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).
Решение
1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).
Второй участок — равномерное движение: v = 8 м/с; a2 = 0.
Третий участок — торможение до остановки (равнозамедленное движение).
2. Путь, пройденный за время движения, будет равен:
Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.
Решение
1. Записываем уравнение скорости для равнозамедленного движения:
Определяем начальную скорость в м/с: vо = 36*1000/3600 = 10 м/с.
Выразим ускорение (замедление) из уравнения скорости: a = — v0/t
2. Записываем уравнение пути: S = vot/2 + at 2 /2. После подстановки получим: S = vot/2
3. Определяем время до полной остановки (время торможения):
Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.
Решение
1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = at = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = at = —10 м/c 2 = const) с начальной скоростью v0 = 20 м/с.
2. Составим зависимость числовых значений s и v для первых 4 с движения
3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав масштабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Например, если расстояние s = 5 м изображать на графике длиной отрезка ls = 10 мм, то 5м = μs*10мм, где коэффициент пропорциональности μs и есть масштаб по оси Os : μs = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изображать на графике длиной lv =10 мм, то 10 м/c = μv * 10 мм и масштаб по оси Ov μv = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком la = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μa = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток времени Δt = 1 с отрезком μt = 10 мм, получим на всех графиках масштаб по осям Ot μt = 0,1 с/мм (0,1 с в 1 мм).
4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сторону).
За 4 с точка прошла путь so_4 = 40 м. Начав движение со скоростью v0 = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.
Если условно принять ускорение свободного падения g = 10 мс 2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение точки, брошенной вертикально вверх со скоростью а0 = 20 м/с.
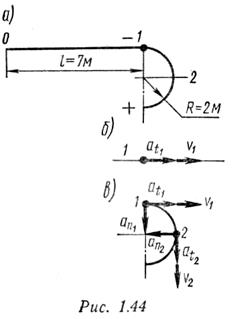
Решение
Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, определим из уравнения движения, подставив частные значения расстояния и времени:
Уравнение изменения скорости
Скорость точки в положении 1
Уравнение изменения касательного ускорения
Касательное ускорение точки в положении 1
Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Скорость и ускорение точки в конце этого участка траектории показаны на рис.1.44, б.
Определим скорость и ускорение точки в начале криволинейного участка траектории. Очевидно, что v1 = 11,5 м/с, аt1 = 14,2 м/с 2 .
Нормальное ускорение точки в начале криволинейного участка
Скорость и ускорение в начале криволинейного участка показаны на рис. 1.44, в (векторы at1 и aa1 изображены без соблюдения масштаба).
Положение 2 движущейся точки определяется пройденным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей центральному углу 90°:
Время, необходимое для перемещения точки из положения 0 в положение2,
Скорость точки в положении 2
Касательное ускорение точки в положении 2
Нормальное ускорение точки в положении 2
Ускорение точки в положении 2
Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и аПг изображены без соблюдения масштаба).

Решение
Уравнение изменения скорости
Время t1 определим из уравнения изменения скорости, подставив частные значения скорости и времени:
Определим положение точки на траектории в момент 3 с:
Дуга окружности длиной 135 м соответствует центральному углу
Уравнение изменения касательного ускорения
Касательное ускорение точки в момент tt
Нормальное ускорение точки в момент tt
Ускорение точки в момент tx
Скорость и ускорение точки в момент времени t1 показаны на рис. 1.45, б.
Как видно из рис. 1.45, б
Пример 8. В шахту глубиной H = 3000 м с поверхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверхности земли. Скорость звука 333 м/с.
Решение
Уравнение движения свободно падающего тела
Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравнения движения:
Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука
Время достижения звуком поверхности земли
Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли
Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и ускорение точки в момент времени t = 2 с.
Решение
Для определения траектории точки нужно из уравнений движения исключить параметр t — время.
Выразим t через х из первого уравнения:
и подставим это значение во второе уравнение:
Траекторией точки является парабола, симметричная относительно оси х.
Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям
Находим скорость точки
При t = 2 с получаем
Находим составляющие ускорения точки
Контрольные вопросы и задания
1. Запишите формулу ускорения при прямолинейном движении.
2. Запишите формулу ускорения (полного) при криволинейном движении.
3. 
4. Параметры движения не меняются.
4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение.
5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).
7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).
источники:
http://spadilo.ru/peremeshhenie-i-put-pri-ravnouskorennom-pryamolinejnom-dvizhenii/
http://mydocx.ru/12-105317.html
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Найти минимальное расстояние между движущимися авто…
|
|
12/03/08 |
|
|
|
|
|
Brukvalub |
|
||
01/03/06 |
Я бы «остановил» один из автомобилей, тогда движение второго относительно «остановленного» будет происходить по прямой, и достаточно найти ближайшую из достижимых в процессе движения точек этой прямой до «остановленного» авто.
|
||
|
|
|||
|
Зангези |
|
|
14/09/07 |
По-моему, проще для понимания и общности ввести в задачу прямоугольную систему координат, тем паче, что движение осуществляется в перпендикулярных направлениях. Ваша задача сведётся к построению функции расстояния между двумя точками, лежащими на осях системы, от времени и поиску её минимума.
|
|
|
|
|
sergey1 |
|
|
14/02/06 |
Найдите расстояние между автомобилями в момент времени t по формуле расстояния между двумя точками, а потом исследуйте полученное выражение на минимум, например, с помощью производной, либо с помощью свойств квадратного трехчлена.
|
|
|
|
|
Ishida Viper-Yuki |
|
|
12/03/08 |
Хм…В общем, суть где-то уловил, но все равно сделать не могу..
|
|
|
|
|
PAV |
|
||
29/07/05 |
Выразите текущие координаты автомобилей как функции от времени.
|
||
|
|
|||
|
bobo |
|
|
01/04/07 |
Я бы все-таки поступил, как посоветовал Brukvalub , тем более, что такое решение годится для произвольного угла между дорогами. Если перейти в систему отсчета, связанную с одним из автомобилей, то второй будет двигаться в этой системе отсчета вдоль прямой, направляющим вектором которой служит вектор разности скоростей второго автомобиля минус первого. А наименьшее растояние между автомобилями за время движения будет расстояние от неподвижной точки до луча (нарисуйте картинку и все станет ясно).
|
|
|
|
|
Ishida Viper-Yuki |
|
|
12/03/08 |
Цитата: нарисуйте картинку и все станет ясно В этом вся проблема.
|
|
|
|
|
Алексей К. |
|
|
29/09/06 |
Чуток помогу — у меня 4 выходных впереди и от этого настроение очень хорошее. А у парня работы больно много…
Первый автомобиль пустим по оси абсцисс (ОХ) из точки с координатами (Право же, метод относительного движения для нас слишком сложен. Попробуем так, потом и теорию относительности осилим
|
|
|
|
|
bobo |
|
|
01/04/07 |
Нарисуйте 2 точки (Ваши автомобили). С началом в этих точках нарисуйте векторы скоростей каждого автомобиля. Найдите вектор, равный разности 2-го вектора минус первый. Нарисуйте его с началом во второй точке. Проведите прямую вдоль этого вектора.Это и будет траэктория относительного движения.
|
|
|
|
|
Ishida Viper-Yuki |
|
|
12/03/08 |
|
|
|
|
|
Алексей К. |
|
|
29/09/06 |
Ну? Алексей К. писал(а): Тогда расстояние между автомобилями в любой момент времени равно…
|
|
|
|
|
Ishida Viper-Yuki |
|
|
12/03/08 |
Цитата: Тогда расстояние между автомобилями в любой момент времени равно… ***
|
|
|
|
|
Brukvalub |
|
||
01/03/06 |
Теперь напишите формулу квадрата расстояния между этими точками и исследуйте ее методами дифференциального исчисления на минимум.
|
||
|
|
|||
|
Алексей К. |
|
|
29/09/06 |
Ishida Viper-Yuki писал(а): y=x Это быстренько убрали, пока никто не видит (отредактировать сообщение, заменить текст на «извините, ошибся»), взяли тайм-аут, тетрадку для рисования и хорошо подумали (кресло имеется?). Ishida Viper-Yuki писал(а): Задач на эту тему в школе не решал вообще, даже не слышал о них, мягко говоря… Это задачка из учебника киллерского мастерства (во второй машине едет бизьнесмен).
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |



































































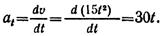

















 в направлении перекрёстка, в роли которого выступает начало координат. Тогда координаты автомобиля в зависимости от времени выразятся так:
в направлении перекрёстка, в роли которого выступает начало координат. Тогда координаты автомобиля в зависимости от времени выразятся так:
 в …
в …
