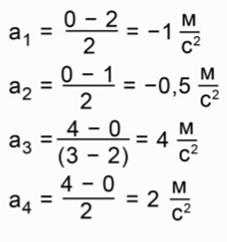В этой статье мы узнаем, как найти ускорение на графике скорости от времени, используя несколько примеров, и решим некоторые задачи.
Ускорение — это разность скоростей, изменяющаяся во времени; следовательно, по графику скорость-время мы можем найти ускорение, измерив наклон графика.
График скорости во времени для положительного ускорения
Давайте посмотрим, как найти ускорение по графику скорость-время. Ниже приводится график зависимости скорости от времени.

По оси x отложено время в секундах, а по оси y отложена скорость объекта в разное время. Наклон графика определяется выражением m=Δy/Δt. Здесь наклон графика скорость-время дает ускорение объекта.
а = м = ΔV/ΔT = v2-v1/t2-t1
Из приведенного выше графика ускорение будет положительным, если V2>V1 то есть, если скорость объекта увеличивается со временем. То же самое будет отрицательным, если V2<V1, то есть если скорость объекта уменьшается со временем. Это тот случай, когда объект замедляется. Так и в том случае, даже когда объект движется в противоположном направлении от направления его движения.
Подробнее о Как найти ускорение с постоянной скоростью: факты и примеры задач.
1 задачи: Рассмотрим объект круглой формы, покоящийся на вершине холма. К объекту прикладывают силу, чтобы сместить его с места. При приложении силы объект ускоряется вниз к подножию холма. Скорость объекта увеличивается до 4 м/с после прохождения расстояния 16 метров. Постройте график для того же, а затем рассчитайте ускорение объекта, учитывая начальную скорость объекта 2 м/с в определенный момент времени.
Решение: Изменение скорости объекта определяется как.
Скорость, равная 4 м/с, наблюдалась после того, как объект прошел расстояние 16 метров. Следовательно, время, затрачиваемое на перемещение 16 м и ускорение тела, равно
2м/с=16м/т
t=16м/2м/с=8с
Следовательно, скорость объекта в момент времени t = 8 секунд была 4 м/с. Теперь мы можем построить график для того же, что и ниже.
Судя по графику, скорость v1=2 м/с при t1=4 сек и скорость v2=4 м/с при t1=8 сек.
Следовательно, ускорение объекта между временными интервалами от 4 до 8 секунд равно
а = v2-v1/t2-t1 = 4-2/8-4 = 2/4 = 1/2 = 0.5 м/с2
Ускорение тела равно 0.5 м/с.2.
График зависимости скорости от времени для нулевого ускорения
Приведенный ниже график показывает, что скорость объекта не меняется со временем и остается постоянной. Это означает, что между этими интервалами времени ускорения объекта не было.
Приведенный выше график показывает, что скорость объекта остается неизменной все время, поэтому мы получаем прямую линию на графике зависимости скорости от времени. Это ясно указывает на то, что в этом случае график зависимости скорости от времени не дает наклона. Поскольку наклон графика отсутствует, ускорение, равное наклону, равно нулю.
Это означает, что перемещение объекта одинаково для разных интервалов времени, следовательно, скорость постоянна.
2 задачи:Скорость объекта, движущегося по плоской поверхности, оказалась равной 0.5 м/с. Через 5 минут другой наблюдатель обнаружил, что скорость равна 0.5 м/с. Тогда каково ускорение объекта на основе наблюдения?
Решение: V1=0.5 м/с; В2=0.5 м/с, временной интервал t=5 минут=300 секунд.
а=в2-v1/t2-t1= 0.5-0.5/300 =0
Поскольку изменений скорости объекта не наблюдалось, ускорение объекта равно нулю.
Подробнее о ускорение.
График зависимости скорости от времени для отрицательного ускорения
Если объект замедляется со временем, то наклон графика скорость-время будет отрицательным. Это показано на приведенном ниже графике зависимости скорости от времени.
Поскольку разница между конечной и начальной рассматриваемой точкой по оси ординат отрицательна, наклон графика ускорения объекта будет отрицательным.
3 задачи: Рассмотрим объект, замедляющийся со временем, как показано на графике ниже.
Вычислите ускорение тела на пути от А до В.
Решение: Скорость объекта в точке А в момент времени t1= 2 секунды v1=10 м/с и в момент времени t2= 5 секунд v2=4м/с. Поэтому ускорение тела равно
а = v2-v1/t2-t1 = 4-10/5-2= -6/3= -2m/s2
Поскольку скорость объекта со временем уменьшается, ускорение объекта отрицательно и равно -2 м/с.2.
Подробнее о График постоянного отрицательного ускорения: что, как, примеры.
График отрицательной скорости для отрицательного ускорения
Когда объект удаляется от точки назначения по отрицательной оси, смещение объекта принимается как отрицательное по отрицательной оси Y. Если положение объекта отклоняется от направления его движения, то считается, что смещение объекта происходит в отрицательном направлении.
Выше приведен график зависимости скорости от времени для отрицательного ускорения. Видно, что скорость со временем уменьшается, наклон графика оказывается отрицательным, а значит, и ускорение отрицательное.
График отрицательной скорости во времени для положительного ускорения
Ниже приведен график зависимости отрицательной скорости от времени в секунду, который дает положительное ускорение.
Поскольку замедляющийся объект однажды начинает ускоряться обратно за счет какого-то внешнего силы, то ускорение, равное наклону График зависимости скорости от времени положителен, потому что скорость объекта продолжает расти со временем.
Подробнее о Отрицательная скорость и нулевое ускорение: как, когда, пример и проблемы.
Часто задаваемые вопросы
Q1. Из приведенного ниже графика вычислите ускорение объекта из точки О в А, из А в В и из В в С; а затем вычислить среднее ускорение объекта от O до C.
Решение: От О до А, v1=0 при t1=0; в2=8 м/с при t2= 4s
Следовательно, ускорение тела из точки О в точку А равно
а = v2-v1/t2-t1=8-0/4-0=8/4=2m/s2
От А до Б, в1=8 м/с при t1=4с; в2=5 м/с при t2= 8s
Следовательно, ускорение тела из точки А в точку В равно
а=в2-v1/t2-t1=5-8/8-4=-3/4=-0.75m/s2
От B до C, v1=5 м/с при t1=8с; в2=5 м/с при t2= 12s
Следовательно, ускорение тела из точки В в С равно
а=в2-v1/t2-t1=5-5/12-8=0/4=0
Среднее ускорение графика от O до C равно
Aсредний= aoa+aab+abc/3
=2-0.75+0/3=1.25/3=0.42m/s2
Следовательно, среднее ускорение тела от О до А равно 0.42 м/с.2.
Почему ускорение является векторной величиной?
Ускорение имеет величину и направление.
Направление ускорения такое же, как и направление скорости после изменения; следовательно, это векторная величина.
Решение задач на определение ускорения, мгновенной скорости и перемещения при равноускоренном прямолинейном движении
Задача на определение пути и перемещения
Задача 1 посвящена исследованию пути и перемещения.
Условие: тело движется по окружности, проходя ее половину. Необходимо определить отношение пройденного пути к модулю перемещения.
Обратите внимание: дано условие задачи, но нет ни одного числа. Такие задачи будут встречаться в курсе физики довольно часто.
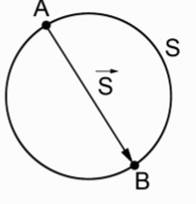
Рис. 1. Путь и перемещение тела
Введем обозначения. Радиус окружности, по которой движется тело, равен R. При решении задачи удобно сделать рисунок, на котором окружность и произвольную точку, из которой движется тело, обозначим А; тело движется в точку В, а S – это половина окружности, S
Несмотря на то, что в задаче ни одного числа нет, тем не менее, в ответе мы получаем вполне определенное число (1,57).
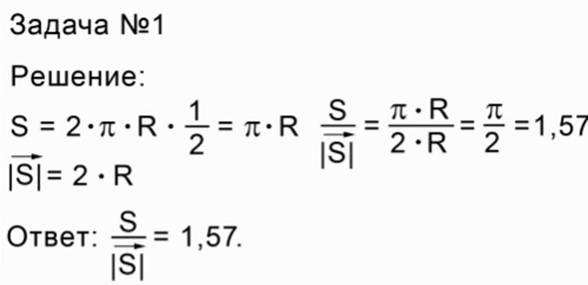
Задача на график скорости
Задача 2 будет посвящена графикам скорости.
Условие: два поезда движутся навстречу друг другу по параллельным путям, скорость первого поезда – 60 км/ч, скорость второго – 40 км/ч. Ниже представлены 4 графика, и нужно выбрать те, на которых правильно изображены графики проекции скорости движения этих поездов.

Рис. 2. К условию задачи 2
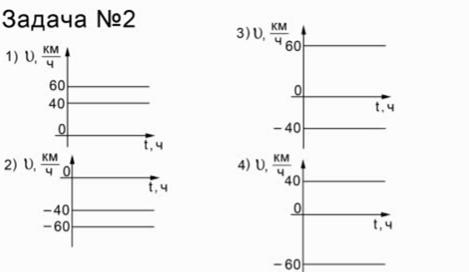
Рис. 3. Графики к задаче 2
Ось скорости – вертикальная (км/ч), а ось времени – горизонтальная (время в ч).
На 1-м графике две параллельные прямые, это модули скорости движения тела – 60 км/ч и 40 км/ч. Если вы посмотрите на нижний график, под номером 2, то увидите то же самое, только в отрицательной области: -60 и -40. На двух других графиках 60 сверху и -40 снизу. На 4-м графике 40 в верхней части, а -60 внизу. Что же можно сказать об этих графиках? Согласно условию задачи два поезда едут навстречу друг другу, по параллельным путям, поэтому если мы выберем ось, связанную с направлением скорости одного из поездов, то проекция скорости одного тела будет положительной, а проекция скорости другого отрицательной (поскольку сама скорость направлена против выбранной оси). Поэтому ни первый график, ни второй к ответу не подходят. Когда проекция скорости имеет одинаковый знак, нужно говорить о том, что два поезда движутся в одну сторону. Если мы выбираем систему отсчета, связанную с 1 поездом, то тогда величина 60 км/ч будет положительной, а величина -40 км/ч – отрицательной, поезд едет навстречу. Или наоборот, если мы связываем систему отчета со вторым поездом, то у одного из них проекция скорости 40 км/ч, а у другого -60 км/ч, отрицательная. Таким образом, подходят оба графика (3 и 4).
Ответ: 3 и 4 графики.
Задача на определение скорости при равнозамедленном движении
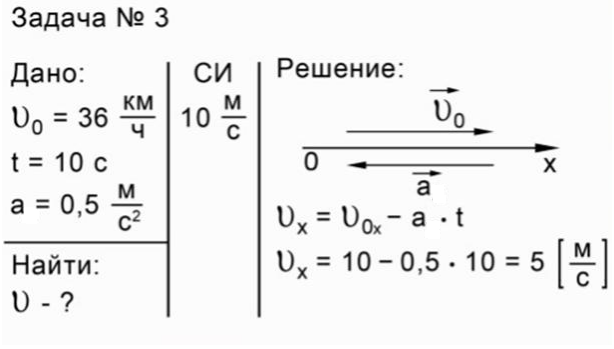
Задача 3.
Условие: автомобиль движется со скоростью 36 км/ч, и в течение 10 с тормозит с ускорением 0,5 м/с2. Необходимо определить его скорость в конце торможения.
В данном случае удобнее выбрать ось ОХ и направить начальную скорость вдоль этой оси, т.е. вектор начальной скорости будет направлен в ту же сторону, что и ось. Ускорение будет направлено в противоположную сторону, ведь автомобиль замедляет свое движение. Проекция ускорения на ось ОХ будет со знаком минус. Для нахождения мгновенной, конечной скорости воспользуемся уравнением проекции скорости. Запишем следующее: Vx= V0x— at. Подставляя значения, получаем конечную скорость 5 м/с. Значит, через 10 с после торможения скорость будет 5 м/с. Ответ: Vx = 5 м/с.
Задача на определение ускорения по графику скорости
Задача 4.
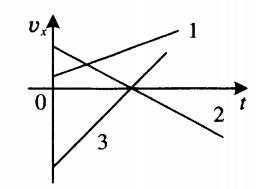
На графике представлены 4 зависимости скорости от времени, и необходимо определить, у какого из этих тел максимальное, а у какого минимальное ускорения.
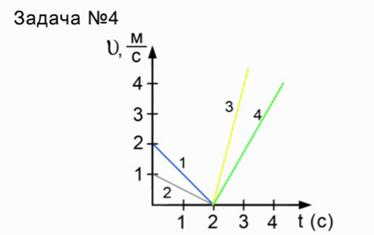
Рис. 4. К условию задачи 4
Для решения необходимо рассмотреть все 4 графика поочередно.
Для сравнения ускорений нужно определить их значения. Для каждого тела ускорение будет определяться как отношение изменения скорости ко времени, в течение которого это изменение произошло. Ниже проведены расчеты ускорения для всех четырех тел:
Как видим, у второго тела модуль ускорения минимальный, а у третьего тела – максимальный.
Ответ: |a3| — max, |a2| — min
Задания
Версия для печати и копирования в MS Word
Автомобиль движется прямолинейно. На графике представлена зависимость скорости автомобиля от времени. Чему равен минимальный модуль ускорения? Ответ выразите в метрах на секунду в квадрате.
Спрятать решение
Решение.
На всех рассматриваемых интервалах времени скорость автомобиля меняется равномерно, следовательно, ускорение на каждом интервале постоянно. Рассчитаем ускорения:
в интервале от 0 до 10 с:
в интервале от 10 до 20 с:
в интервале от 20 до 30 с:
в интервале от 30 до 40 с:
Минимальный модуль ускорения равен 0,5 м/с2.
Ответ: 0,5.
Гость 13.10.2012 16:25
здравствуйте) а почему не с 20 до 30?
там же вроде убывает о.о
Гость
Добрый день!
В данной задаче спрашивают не о минимальном значении проекции ускорения, а о минимальном значении модуля ускорения. Поэтому необходимо сравнивать абсолютные величины.
Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.
Что такое мгновенная скорость? Мгновенная скорость — скорость тела в данный момент времени. Обозначается vмгн. Далее, когда мы будем говорить о скорости, мы будем понимать под ней мгновенную скорость тела и обозначать ее просто — v.
Определение
Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t0 и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:
v = v0 + at
v — скорость тела в данный момент времени, v0 —скорость тела в начальный момент времени, a — ускорение тела, t — время, в течение которого это тело двигалось
Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.
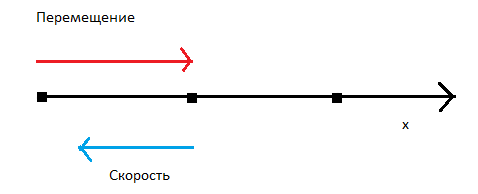
Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.
Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.
Скалярная формула скорости
В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:
v = v0 ± at
Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.
Проекция скорости
Проекция скорости при равноускоренном прямолинейном движении имеет вид:
vx = v0x + axt
Знак проекции скорости зависит от того, в какую сторону движется тело:
- Знак проекции скорости имеет знак «+», если тело движется в сторону направления оси ОХ.
- Знак проекции скорости имеет знак «–», если тело движется противоположно направлению оси ОХ.
Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.
График скорости
График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является прямая.
Определение направления движения тела относительно оси ОХ по графику скорости
- Если график скорости лежит выше оси времени, то тело движется в направлении оси ОХ. На рисунке этому утверждению соответствует график 1.
- Если график скорости пересекает ось времени, то модуль скорости тела сначала уменьшался, и тело тормозило. Но с момента пересечения оси времени оно меняло направление движения в противоположную сторону и двигалось ускоренно. На рисунке этому соответствуют графики скорости 2 и 3.
- Если график скорости лежит ниже оси времени, тело движется в направлении, противоположном направлению оси ОХ. На рисунке тело 3 до пересечения с осью времени двигалось противоположно направлению ОХ. Но тело 2 двигалось противоположно оси только после пересечения с этой осью.
Сравнение модулей ускорения по графикам скоростей
Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.
Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.
На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.
Полезные факты
- Если тело начинало движение из состояния покоя, его начальная скорость равна 0, а его ускорение положительно: v0 = 0, a > 0.
- Если тело заканчивает движение остановкой, то его мгновенная скорость в конечный момент времени равна 0, а его ускорение отрицательно: v = 0, a < 0.
- Если тело покоится, его скорость и ускорение равны 0: v0 = 0, a = 0.
Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.
Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:
v = v0 – at
Выразим начальную скорость:
v0 = v + at
Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:
v0 = 0 + 2 ∙ 5 = 10 (м/с)
Задание EF18553

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные и перевести их единицы измерения величин в СИ.
2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.
3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.
4.Определить перемещение тела и его кинетическую энергию.
5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x(t)=x0+v0t+at22
Теперь мы можем выделить кинематические характеристики движения тела:
• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).
Перемещение тела определяется формулой:
s=v0t+at22
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x(t)=v0t+at22=5t−3t2
Кинетическая энергия тела определяется формулой:
Ek=mv22
Скорость при прямолинейном равноускоренном движении равна:
v=v0+at=5−6t
Поэтому кинетическая энергия тела равна:
Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2
Следовательно, правильная последовательность цифр в ответе будет: 34.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
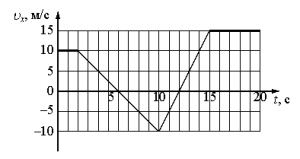
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
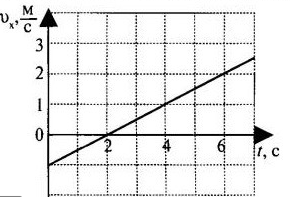
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.1k
Скорость автомобиля разгоняющегося с места
27982. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной lкм с постоянным ускорением a км/ч2, вычисляется по формуле:Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
Выражение «приобрести скорость не менее 100 км/ч» означает, что скорость должна быть 100 или более км/ч. Задача сводится к решению неравенства:

Ответ: 5000
27987. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением aкм/ч , вычисляется по формуле v2=2la. Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 1 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 5000 км/ч2. Ответ выразите в км/ч.
Зависимость скорости от ускорения прямолинейная (чем больше ускорение, тем больше скорость). Поэтому при наименьшем ускорении будет самая минимальная скорость, в данном случае минимальное ускорение 5000 км/ч2. Подставим данные в формулу:
Наименьшая скорость автомобиля 100 км/ч.
Ответ: 100
27989. Автомобиль, масса которого равна m=2160 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S=500 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно:Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 2400 Н. Ответ в секундах.
Из условия ясно, что сила приложенная к автомобилю равна или более 2400Н, то есть F≥2400Н. Задача сводится к решению неравенстварешив его определим наибольшее t:

Время величина неотрицательная, поэтому 0≤t≤30.
Таким образом, наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь 30 секунд.
Ответ: 30
Категория: Физические задачи | ЕГЭ-№8
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.