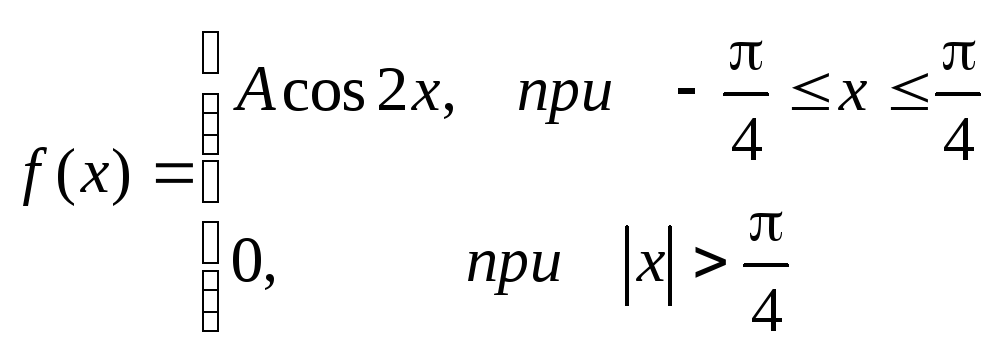Как найти минимальное математическое ожидание - AvtoShod.ru

Как найти математическое ожидание?

Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.

Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).

Нужна помощь? Решаем теорию вероятностей на отлично

Спасибо за ваши закладки и рекомендации

Формула среднего случайной величины

Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$

Пример нахождения математического ожидания

Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.

Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.

Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.

Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$

Другие задачи с решениями по ТВ

Подробно решим ваши задачи по теории вероятностей

Вычисление математического ожидания онлайн

Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.

Введите число значений случайной величины К.
Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
Нажмите на кнопку «Вычислить».
Калькулятор покажет вычисленное математическое ожидание $M(X)$.

Видео. Полезные ссылки

Видеоролики: что такое среднее (математическое ожидание)

Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Лучшее спасибо — порекомендовать эту страницу

Полезные ссылки

А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.

Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Источник

Добрый день.

Я напишу как решается задача нахождения мат.ожидания максимума

, а по аналогии вы сделаете для минимума.
Если долго не будет получаться, напишу потом решение — просто его нет под рукой, а это — есть.
—

Пусть $a$ и $b$ — независимые, одинаково-распределенные равномерно на отрезке случайные величины.

1) Ищем функцию распределения максимума

Вот этот переход может быть неочевиден. Нужно нарисовать прямую, на ней отметить случайные точки a и b.
$x$ в нашем случае лежит правее $a$ и $b$ . Отсюда и вытекает то, что написано.

2) Ищем плотность распределения максимума. Для этого просто дифференцируем функцию распределения:

$rho_{max(a,b)} = 2 x$

3) Ищем мат.ожидание максимума:

$E max(a, b) = int_{0}^{1} (rho_{max(a,b)} cdot x) = int_{0}^{1}(2 x cdot x) = 2/3$

Получен ответ!

Источник

Конечно, можно. Случайные величины здесь подразумеваются независимые (в противном случае надо знать совместное распределение). Случай, когда отрезки не пересекаются, или пересекаются по точке, тривиален. Пусть $%xi$% р.р. на $%[a,b]$%, и $%eta$% р.р. на $%[c,d]$%. Будем различать два случая.

1) Первый отрезок содержит второй: $%ale c < dle b$%. Понятно, что $%zeta=min(xi,eta)$% распределена на $%[a,d]$%, и плотность вне этого отрезка равна нулю. Найдём функцию распределения минимума, равную $%F(t)$%, а затем плотность и матожидание.

Пусть $%tin[a,c]$%. Событие $%{zetale t}$% означает, что $%xile t$%, и вероятность равна $%F(t)=frac{t-a}{b-a}$%. Теперь пусть $%tin(c,d]$%. Вероятность того, что $%zetale t$%, равна $%1-P{xi > t,eta > t}=1-(1-P{xile t})(1-P{etale t})$% в силу независимости, то есть $%F(t)=1-frac{(b-t)(d-t)}{(b-a)(d-c)}$%.

Таким образом, плотность постоянна на $%[a,c]$%, а именно, $%f(t)=frac1{b-a}$% для этих значений, а на $%(c,d]$% плотность линейна и равна $%f(t)=frac{b+d-2t}{(b-a)(d-c)}$%.

Теперь находим матожидание: $%Mzeta=frac1{b-a}intlimits_a^c t,dt+frac1{(b-a)(d-c)}intlimits_c^dt(b+d-2t),dt=frac{3bc+3bd-3a^2-c^2-d^2-cd}{6(b-a)}$%.

2) Теперь пусть первый и второй отрезок перекрываются: $%a < c < b < d$%. Здесь $%zeta$% распределена на $%[a,b]$%, и вне этого отрезка плотность равна нулю. При $%tin[a,c]$% получается $%F(t)=frac{t-a}{b-a}$%, как и в предыдущем случае, то есть $%f(t)=frac1{b-a}$% постоянна. Если $%tin(c,b]$%, то получается $%F(t)=1-frac{(b-t)(d-t)}{(b-a)(d-c)}$%, то есть всё снова обстоит так же, и $%f(t)=frac{b+d-2t}{(b-a)(d-c)}$%.

Матожидание вычисляется аналогично, но с несколько другими пределами интегрирования, и итоговая формула имеет другой вид: $%Mzeta=frac1{b-a}intlimits_a^c t,dt+frac1{(b-a)(d-c)}intlimits_c^bt(b+d-2t),dt=frac{3b^2d+3a^2c+c^3-3a^2d-3bc^2-b^3}{6(b-a)(d-c)}$%.

Источник

We know that $F_{|X|}(x)=Pr(-xleq{X}leq{x})=F_{X}(x)-F_{X}(-x)$

Hence, $f_{|X|}(x)=f_{X}(x)+f_{X}(-x)=2f_{X}(x)$

Therefore,
$f_{|X|}(x)=sqrt{frac{2}{pi}}e^{frac{-x^{2}}{2}}$ and similarly,
$f_{|Y|}(y)=sqrt{frac{2}{pi}}e^{frac{-y^{2}}{2}}$

Then, by symmetry of Normal curve, we can simplify to:

$E[min(|X|,|Y|)] = frac{2}{pi}(int_{x=0}^{infty}int_{y=0}^{x}ye^{frac{-x^{2}}{2}}e^{frac{-y^{2}}{2}}dydx + int_{y=0}^{infty}int_{x=0}^{y}xe^{frac{-x^{2}}{2}}e^{frac{-y^{2}}{2}}dxdy)$

$E[min(|X|,|Y|)] = frac{4}{pi}int_{x=0}^{infty}int_{y=0}^{x}ye^{frac{-x^{2}}{2}}e^{frac{-y^{2}}{2}}dydx$

$E[min(|X|,|Y|)] = frac{4}{pi}int_{x=0}^{infty}e^{frac{-x^{2}}{2}}(1-e^{frac{-x^{2}}{2}})dx$

$E[min(|X|,|Y|)] = frac{4}{pi}int_{x=0}^{infty}(e^{frac{-x^{2}}{2}}-e^{-x^{2}})dx$

$E[min(|X|,|Y|)] = frac{4}{pi}(frac{1}{2})int_{0}^{infty}(sqrt{2pi}frac{1}{sqrt{2pi}}e^{frac{-x^{2}}{2}}-sqrt{pi}frac{1}{sqrt{pi}}e^{-x^{2}})dx$

Since, we have 2 pdf’s:

$Normal(0,1) : frac{1}{sqrt{2pi}}e^{frac{-x^{2}}{2}}$

$Normal(0,frac{1}{2}) : frac{1}{sqrt{pi}}e^{-x^{2}}$

Thus,

$E[min(|X|,|Y|)] = frac{2}{pi}(sqrt{2pi}-sqrt{pi})$

$E[min(|X|,|Y|)] = frac{2({sqrt{2}-1})}{sqrt{pi}}$

Hence, proved.

Источник

Математическое ожидание, дисперсия, среднее квадратичное отклонение

Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.

Математическое ожидание Mдискретной случайной величины — это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.

Свойства математического ожидания:

Математическое ожидание постоянной
величины равно самой постоянной .
Постоянный множитель можно выносить
за знак математического ожидания .
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий .
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых

Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.

Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.

Принимая во внимание свойства
математического ожидания, легко показать
что

Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.

Свойства дисперсии:

Дисперсия постоянной равна нулю.
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат.
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.

Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное.

Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.

Решение задач:

1)Дана случайная величина Х:

x_i	-3	-2	0	1	2
p_i	0,1	0,2	0,05	0,3	0,35

Найти М(х), D(X).

Решение:

=9=2,31.

2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.

Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.

Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.

Решение:D(Z)=6²D(Х)-2²D(Y)+0=180-8=172.

Тема 7. Непрерывные случайные величины

Задача 14

Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.

Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).

Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.

Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.