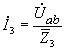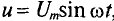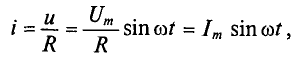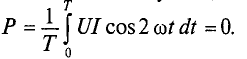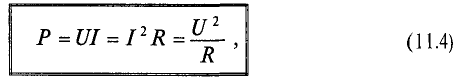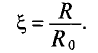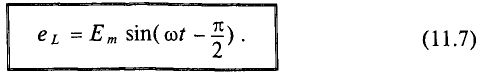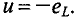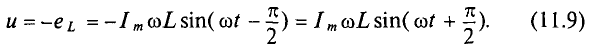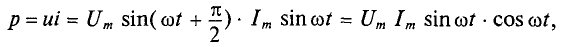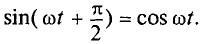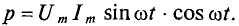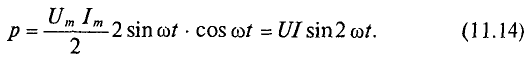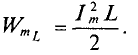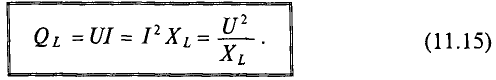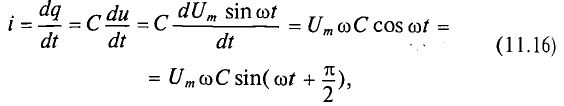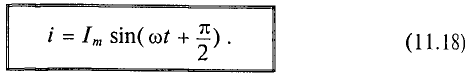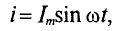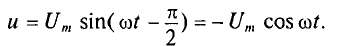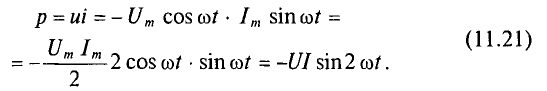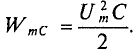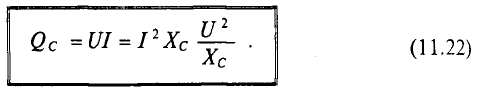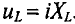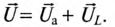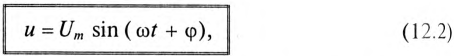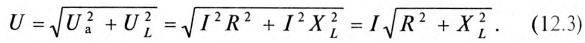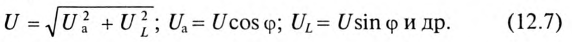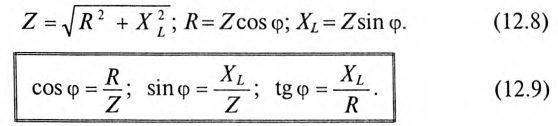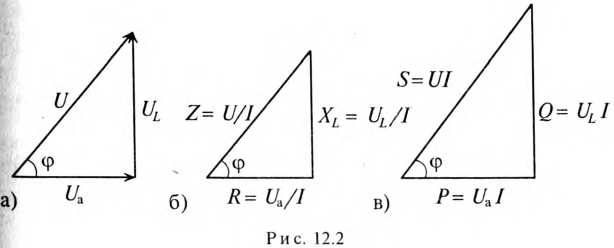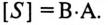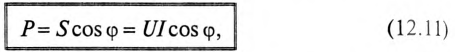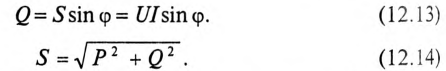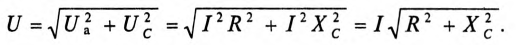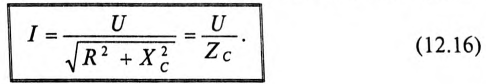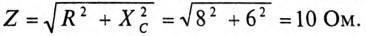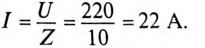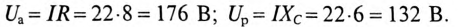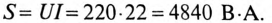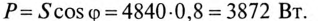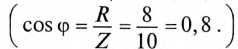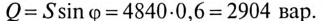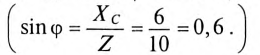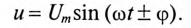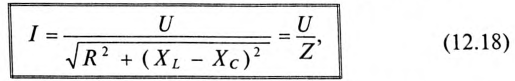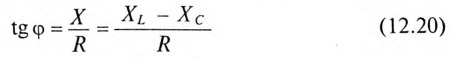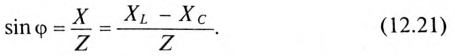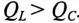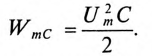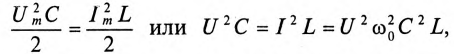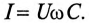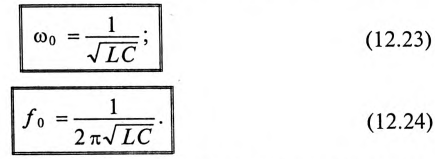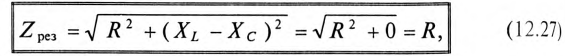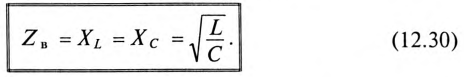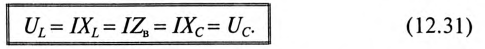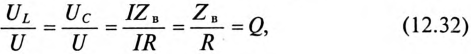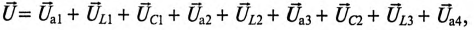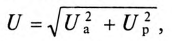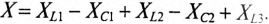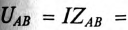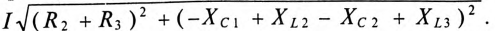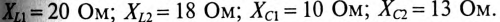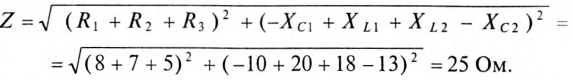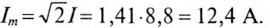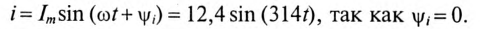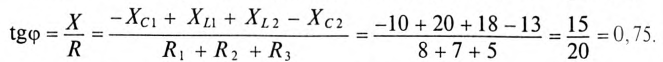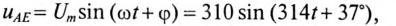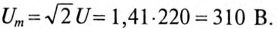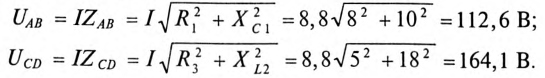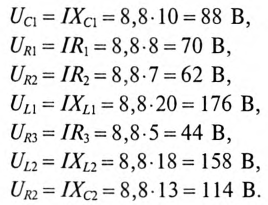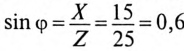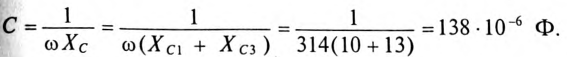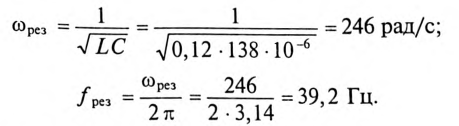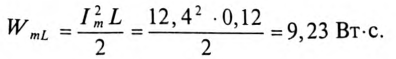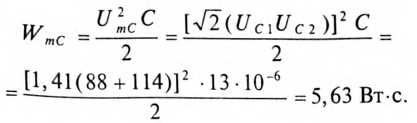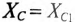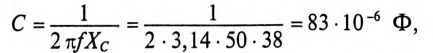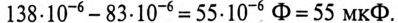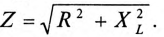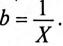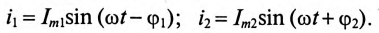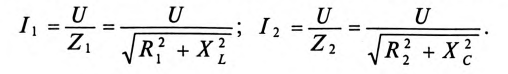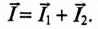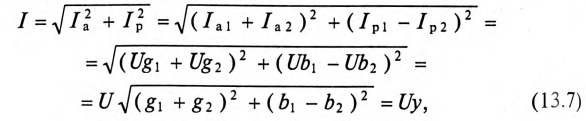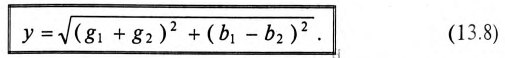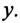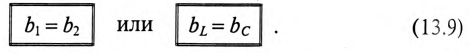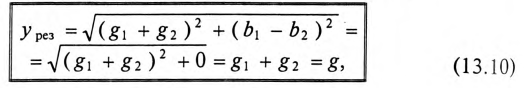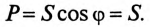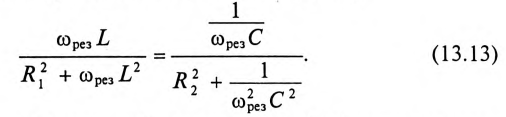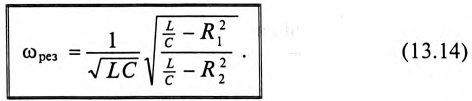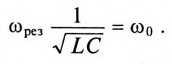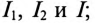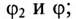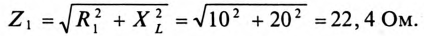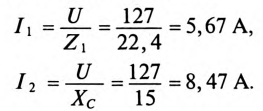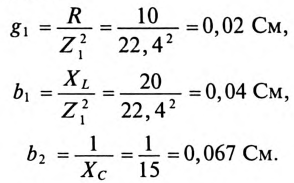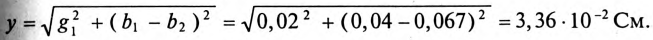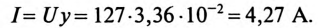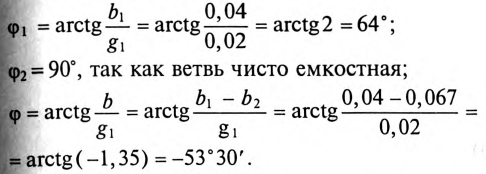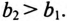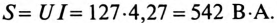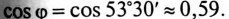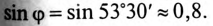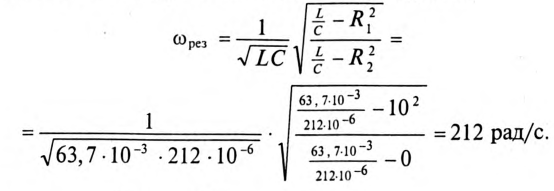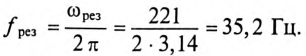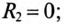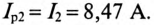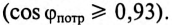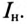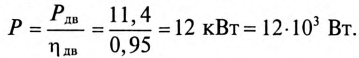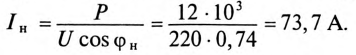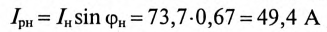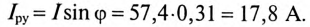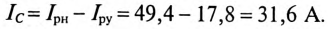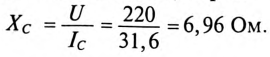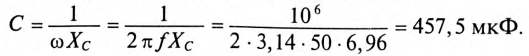Мгновенная мощность
В отличие от цепей постоянного тока, где мощность в течение определенного промежутка времени остается неизменной, в цепях переменного тока дело обстоит иначе. Так как ток и напряжение постоянно меняют своё значение, то и мощность соответственно будет меняться в каждый момент времени. Такая мощность называется мгновенной.
Мгновенной мощностью p(t) называют произведение приложенного к цепи мгновенного напряжения u(t) на мгновенное значение тока i(t) в этой цепи.
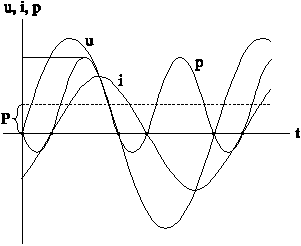
График мгновенной мощности представлен на рисунке ниже

Мощность обозначена заштрихованной областью. Знак мощности зависит от сдвига фаз между током и напряжением. В данном случае в цепи присутствуют только активные сопротивления, которые не создают сдвига фаз, поэтому мощность имеет только положительные значения.
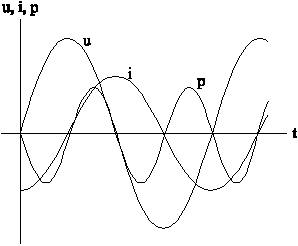
Рассмотрим другой график
На данном графике имеются области отрицательных значений мгновенной мощности. Такой график может соответствовать цепи, в которой присутствуют конденсатор или катушка, причем положительные участки — это мощность, которая пошла в цепь и рассеялась на сопротивлении, либо запаслась в качестве энергии полей конденсаторов или катушек, а отрицательные участки это мощность, которая была возвращена обратно источнику.
Активная мощность
Чтобы понять какое количество энергии потребляет источник, целесообразнее взять среднюю мощность за период. Для этого вернемся к первому графику.
На графике мгновенной мощности выделяют прямоугольник со сторонами T и Pm/2. Часть графика, которая находится выше линии Pm/2 точно укладывается в незаштрихованную часть прямоугольника. Таким образом, с помощью линии Pm/2 мы можем определить среднюю мощность за период, которая называется активной мощностью. Активная мощность – это полезная мощность, которая идет на преобразование в другие виды энергии.
В нашем случае сдвиг фаз равен нулю, поэтому коэффициент мощности равен единице, но в случаях с реактивными элементами нужно этот момент учитывать.
Активная мощность измеряется в ваттах – Вт.
cosφ – коэффициент мощности, который показывает отношение активной мощности к полной мощности.
Реактивная мощность
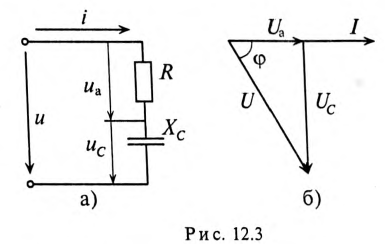
Реактивная мощность – это энергия, которая периодически циркулирует между источником и приемником. Реактивная мощность возникает потому, что конденсатор и катушка способны накапливать энергию, а затем снова отдавать её в сеть. На практике от реактивной мощности зачастую стараются избавиться.
Реактивная мощность измеряется в вольт амперах реактивных – ВАр.
Полная мощность
Полная мощность — это максимальное значение активной мощности.
Полная мощность измеряется в вольт-амперах — ВА.
Для наглядного представления существует треугольник мощностей, в котором гипотенузой является полная мощность, а катетами – активная и реактивная составляющие.

Читайте также — Последовательная RL-цепь
Мгновенное значение мощности.
При
синусоидальных токах и напряжениях
,
как и для любой цепи.
Подставив
в это выражение синусоидальный ток
через какой-либо участок цепи и напряжение
на этом участке, получим, приняв, что
ток отстает от напряжения на угол :
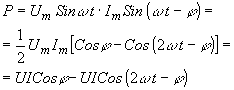
Рис.
4-8
Из
формулы и осциллограммы видно, что
мгновенная мощность состоит из двух
слагаемых: одно, не зависящее от времени,
— постоянная составляющая, а другое —
синусоидальная функция времени двойной
частоты. График p проходит через ноль в
точках, где пересекают ось абсцисс либо
ток, либо напряжение (рис. 4-8).
Интересно
отметить, что если ток и напряжение
сдвинуты по фазе на угол (чисто
емкостная или чисто индуктивная цепь),
то первое слагаемое равно нулю (рис.
4-9).
Из
формулы:
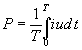
следует,
что для измерения мощности требуется
иметь прибор, перемножающий две функции
времени и вычисляющий среднее значение
(постоянную составляющую) такой функцию.
Для
измерения мощности в реальных цепях
применяют электродинамические ваттметры.
Они состоят из двух магнитно-связанных
катушек, одна из которых может вращаться
вокруг оси. С подвижной катушкой связана
стрелка, показывающая на шкале угол ее
отклонения от нулевого положения,
которое поддерживается специальной
пружинкой.
Противодействующий
момент пружинки по закону Гука
пропорционален углу отклонения стрелки
— .
Вращающий
момент определяется изменением энергии
запасенной системой при пропускании
токов через катушки при повороте
подвижной катушки
.
Равновесие
достигается при .
.
Энергия,
запасенная системой двух катушек:
.
Первые
два слагаемых от угла не
зависят
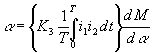
Т.к.
механическая инерционность системы
приведет к тому, что угол отклонения
стрелки будет пропорционален среднему
значению момента.
Таким
образом, если через одну из катушек
пропускать ток пропорциональный току
приемника, а через другую — пропорциональный
его напряжению, получим (в предположении ),
что уголбудет
пропорционален активной мощности
.
На
рис. 4-11 показана схема включения
ваттметра. Точками (или звездочками)
отмечены зажимы, которые следует
объединить, т.к. направление вращающегося
момента зависит от согласования
направлений тока и напряжения.
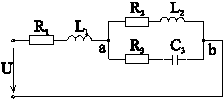
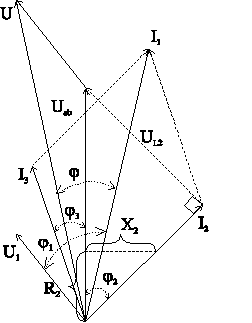
13. Комплексный метод расчета при последовательно-параллельном соединении двухполюсников. Построение векторной диаграммы.
(рассмотрим
поподробнее) (рис. 4-18) при
.
Рис.
4-18
Комплексные
сопротивления двухполюсников:
,
,
.
Сопротивление
двухполюсника аb:
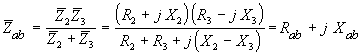
Эквивалентное
сопротивление всей цепи:
.
Входной
ток — ток через первый двухполюсник:
,
где
;
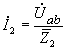
или
по формуле делителя тока:
;
.
Мощности:
;
;
;
;
;
.
Мощности
источника U:
;
.
“Успех”
построения векторной диаграммы
(желательно не зависимо от алгебраического
расчета) определяется порядком построения
(рис. 4-19).
Рис.
4-19
1.
Возьмем за основу вектор произвольной
величины.
2.
Вектор тока отстает
от него на угол.
3.
Вектор тока опережает
напряжениена
угол.
Для
построения углов нет необходимости их
вычислять. Достаточно построить
треугольники сопротивлений. Соотношение
между величинами векторов и
надо
соблюсти в соответствии с пропорцией:.
4.
Сложив вектора и
в
соответствии с первым законом Кирхгофа,
получим:.
5.
Угол определит
направление вектора напряжения,
относительно тока,
величина вектораопределится
из соотношения.
6.
Геометрическим сложением определим ,
остается задаться конкретным масштабом,
приравняв,
и выбрать масштаб тока. Полученная
диаграмма с точностью до геометрических
построений дает ответы обо всех величинах
токов и напряжений и их относительных
фазах. Например, перпендикуляр из конца
векторана
направление токадаст
напряжение на катушке.
Векторную диаграмму можно использовать
для проверки правильности алгебраических
расчетов. Например, уголмежду
токоми
входным напряжениемдолжен
быть равен.
Мощность переменного тока
-
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
-
Мощность тока через резистор
-
Мощность тока через конденсатор
-
Мощность тока через катушку
-
Мощность тока на произвольном участке
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.
Пусть и
— мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени
— настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины
и
можно считать постоянными в течение интервала
.
Пусть за время через наш участок прошёл заряд
(в соответствии с правилом выбора знака для силы тока заряд
считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу
Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:
(1)
Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.
Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.
1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).
2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.
Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).
Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.
к оглавлению ▴
Мощность тока через резистор
Пусть переменный ток протекает через резистор сопротивлением
. Напряжение на резисторе, как нам известно, колеблется в фазе с током:
Поэтому для мгновенной мощности получаем:
(2)
График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.
Рис. 1. Мощность переменного тока через резистор
Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:
На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается
колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между
и
. Где же именно?
Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?
Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:
среднее значение квадрата синуса (или косинуса) за период равно .
Этот факт иллюстрируется рисунком 2.
Рис. 2. Среднее значение квадрата синуса равно
Итак, для среднего значения мощности тока на резисторе имеем:
(3)
В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):
(4)
Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:
Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением
, то в обоих случаях лампочка будет гореть одинаково ярко.
Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.
к оглавлению ▴
Мощность тока через конденсатор
Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на
:
Для мгновенной мощности получаем:
График зависимости мгновенной мощности от времени представлен на рис. 3.
Рис. 3. Мощность переменного тока через конденсатор
Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.
Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).
Рис. 4. Напряжение на конденсаторе и сила тока через него
Рассмотрим последовательно все четыре четверти периода.
1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.
Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.
2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.
Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).
3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.
Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.
4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.
Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.
Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
к оглавлению ▴
Мощность тока через катушку
Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на
:
Для мгновенной мощности получаем:
Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).
Рис. 5. Напряжение на катушке и сила тока через неё
Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.
В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.
Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.
к оглавлению ▴
Мощность тока на произвольном участке
Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .
Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:
Тогда для мгновенной мощности имеем:
(5)
Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:
В результате получим:
(6)
Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:
(7)
Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:
Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки
, и средняя мощность равна нулю.
Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.
С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Мощность переменного тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Мощность, формула
Мощностью P называется отношение произвольной работы W к времени t, в течение которого совершается работа.
[
textit{Мощность} = frac{textit{Работа}}{textit{Время}}
]
Единица СИ мощности
[
[P] = text{Ватт} enspace text{(Вт)} = frac{text{Джоуль}}{text{секунда}} = text{кг} frac{м^2}{с^3}
]
Средняя мощность, формула
Если:
P — Средняя мощность (Ватт),
W — Работа (Джоуль),
t — Время затраченное на совершение работы (секунд),
то
[
average{P} = frac{W}{t}
]
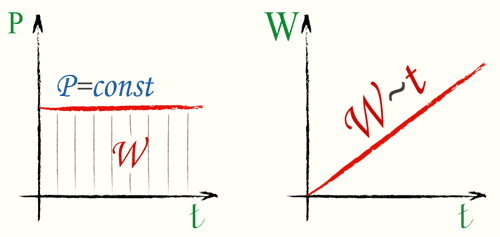
Вычислить, найти среднюю мощность по формуле (3)
Мгновенная мощность, формула
В большинстве случаев мощность зависит от времени, P=P(t).
Мгновенная мощность есть производная работы по времени:
[
P = frac{dW}{dt} = dot{W}
]
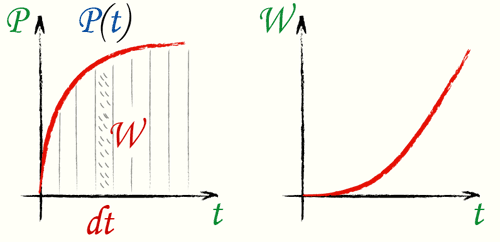
Поскольку см. (Работа)
[
dW = Fds
]
то отсюда следует см. (Мгновенная скорость)
[
P = F frac{ds}{dt} = Fu
]
Здесь:
F — Мгновенная сила (Ньютон),
u — мгновенная скорость (метр/секунда),
Мгновенная мощность равна произведению мгновенной силы на мгновенную скорость
При равномерно ускоренном движении F=const
[
P_{max} = F u_{max} ; average{P} = F average{u}
]
Вычислить, найти мгновенную мощность, по формуле (6)
Мощность |
стр. 471 |
|---|
Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
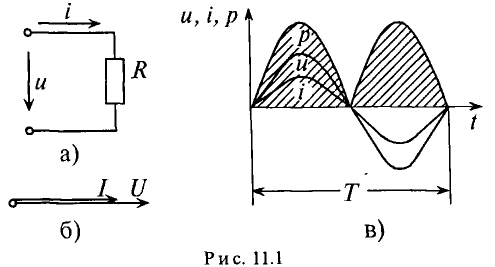
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение
где
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (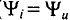
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:
Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 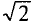
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 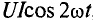
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 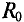
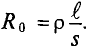
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е.
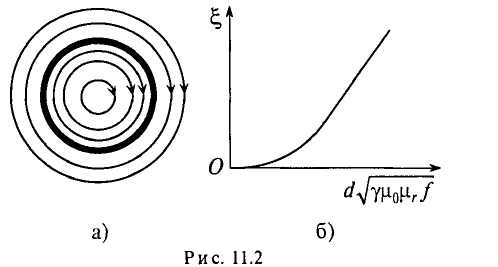
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 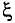
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости 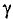
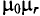

При токах большой частоты 
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
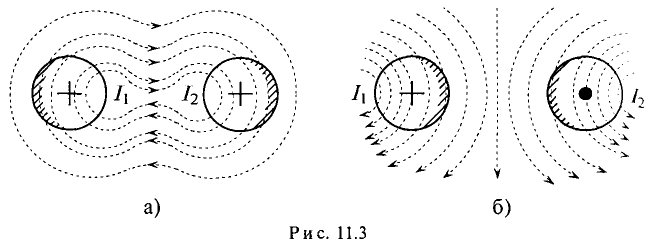
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
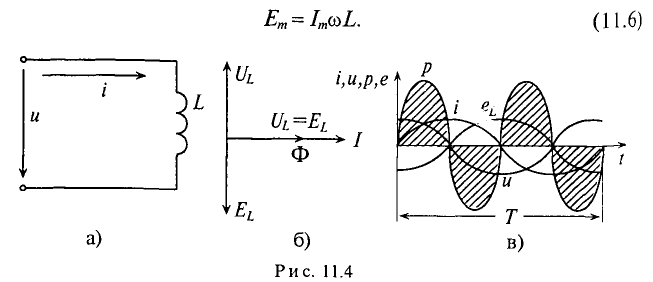
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 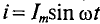
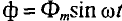
так как
Очевидно, эта ЭДС достигает своего амплитудного значения 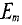
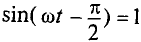
Тогда
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 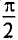
По второму закону Кирхгофа для мгновенных значений можно записать
Откуда
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 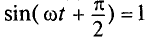
Следовательно,
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 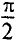
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 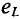
Если уравнение (11.10) разделить на 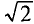
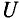
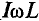
Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Таким образом,
Закон Ома для этой цепи можно записать иначе:
Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
где
Следовательно,
Полученное уравнение умножают и делят на 2:
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (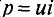
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 — конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 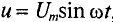
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 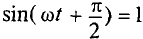
Тогда
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° = 
Если уравнение (11.17) разделить на 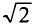
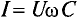
Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:
Когда закон Ома для цепи с конденсатором можно записать:
Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
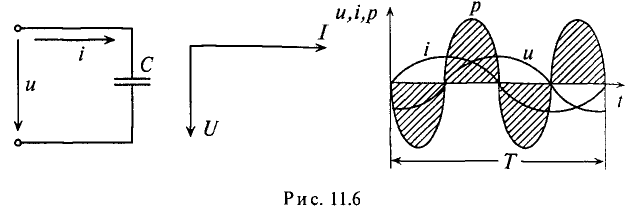
Если в цепи конденсатора емкостью 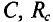
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
Мгновенная мощность в цепи с конденсатором
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) — аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
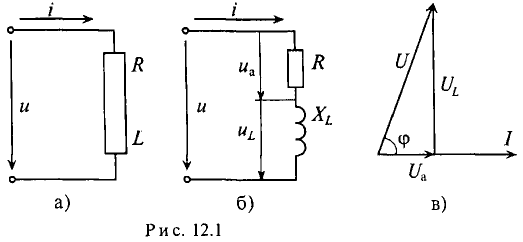
Цепь с активным сопротивлением и индуктивностью
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 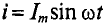
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать
Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 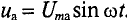
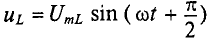
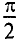
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 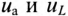
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 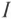
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
Откуда
Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:
где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать
где Z — кажущееся сопротивление этой цепи.
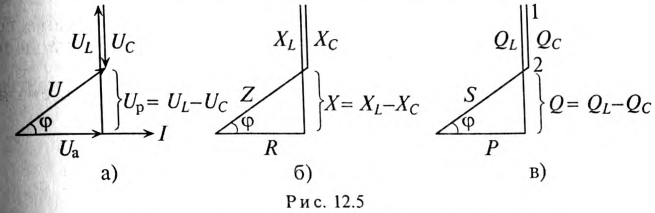
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи
которая измеряется в вольт-амперах, т.е.
Однако потребляется в цепи только часть полной мощности — активная мощность
где cos ф показывает, какая часть полной мощности 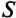
Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 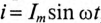
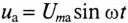
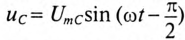
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф < 90°, т. е.
Действующее значение напряжения U, приложенного к этой цепи, определяется по векторной диаграмме (рис. 12.3):
Откуда математическое выражение закона Ома для этой цепи:
Пример 12.1
К цепи с последовательно включенными сопротивлениями R= 8 Ом и Хс= 6 Ом (рис. 12.3а) приложено напряжение U= 220 В. Определить ток цепи I, напряжение на активном 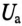
Решение
Для определения тока вычислим полное сопротивление цепи
Тогда ток будет равен
Напряжения на участках:
Полная мощность
Активная мощность
Реактивная мощность
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток 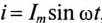
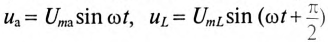
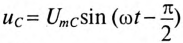
Мгновенное значение напряжения цепи определяется по формуле
Так как в рассматриваемой цепи включены два реактивных сопротивления XL и Хс, то возможны три режима работы цепи:
Векторная диаграмма цепи для режима 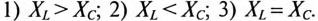
Знак перед углом сдвига фаз ф зависит от режима работы цепи Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е. 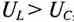
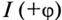
Если в цепи преобладает емкостное напряжение (сопротивление), т.е. 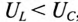
Из векторной диаграммы (рис. 12.46) следует:
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
где Z — полное (или кажущееся) сопротивление неразветвленной цепи с R, L и С, т. е.
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла ф можно определить из треугольника сопротивлений (рис. 12.56):
или
Из выражений (12.20) и (12.21) видно, что если 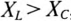
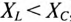
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности 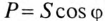
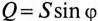
Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= QL— Qc. Эта реактивная мощность (энергия) колеблется между источником и магнитным полем катушки индуктивности, так как
Полная мощность цепи определяется по формуле
Колебательный контур
Электрические цепи, в которых происходят периодические изменения токов, напряжений, энергии называются колебательными.
Для того чтобы исследовать резонансные явления, необходимо иметь представления о процессах в колебательном контуре, состоящем из идеальной катушки и конденсатора без потерь.
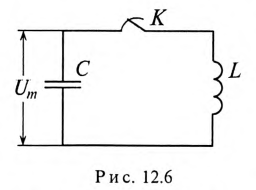
Если конденсатор емкостью С зарядить до напряжения Um, то в электрическом поле этого конденсатора накопится энергия, максимальное значение которой согласно выражению (6.21):
Если к заряженному конденсатору подключить индуктивность L замыканием ключа К (рис. 12.6), то конденсатор будет
разряжаться через индуктивность переменным током i. При этом в индуктивности L создается ЭДС самоиндукции eL, и в магнитном поле ее накапливается энергия, максимальное значение которой (9.12):
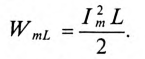
Источником энергии в этом контуре является конденсатор. Ток в контуре, состоящем из индуктивности L и конденсатора С, не прекращается даже когда конденсатор полностью разрядится. За счет ЭДС самоиндукции и энергии, накопившейся в магнитном поле индуктивности, конденсатор будет заряжаться, и энергия магнитного поля индуктивности переходит в электрическое поле конденсатора. При этом источником энергии в этом контуре является индуктивность. Дальше процесс повторяется.
Таким образом, в замкнутом контуре, состоящем из индуктивности и емкости, происходит колебание энергии между электрическим полем конденсатора С и магнитным полем индуктивности L. Поэтому такой замкнутый контур называется колебательным контуром.
Колебание энергии в колебательном контуре происходит с определенной частотой 
так как из (11.19) в цепи переменного тока с емкостью
Откуда
Таким образом, частота собственных колебаний колебательного контура определяется параметрами этого контура L и С.
Если в колебательном контуре отсутствуют потери (идеальный контур), то колебания в нем будут незатухающими с неизменной амплитудой. Если в колебательном контуре имеется активное сопротивление, т.е. возникают потери, то колебания энергии в нем будут затухающие, с уменьшающейся амплитудой, если эти потери не компенсируются.
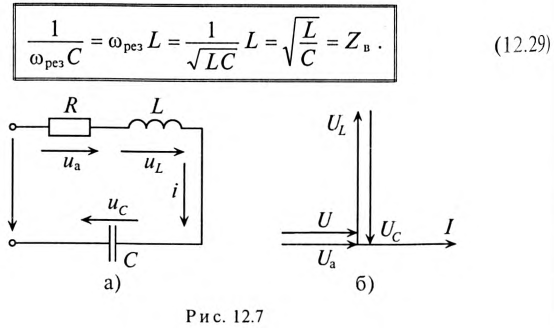
Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R И индуктивностью L (рис. 12.7а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.
Из (12.25) следует 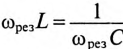
Из (12.26) следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 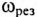
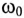
Полное (кажущееся) сопротивление цепи (рис. 12.7а) при резонансе напряжений определяется по формуле
так как XL-Xc=0.
То есть полное сопротивление неразветвленной цепи при резонансе напряжений 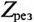
Следовательно, ток в неразветвленной цепи при резонансе напряжений максимальный:
Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
(12.29)
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 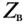
Напряжения на индуктивности UL и на емкости Uc при резонансе напряжений равны между собой, так как равны сопротивления, см. (12.25).
Равенство (12.31) определяет название «резонанс напряжений».
Так как UL и Uc изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 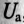
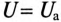
При резонансе напряжений каждое из реактивных напряжений UL и Uc может оказаться большим, чем напряжение цепи U.
где Q — добротность резонансного контура.
Добротность контура Q показывает, во сколько раз напряжение на индуктивности UL и емкости Uc (каждое) больше напряжения цепи U.
Высокая добротность резонансного контура (при малом активном сопротивлении контура) нашла широкое применение в радиотехнике, в частности в антенном контуре.
Из векторной диаграммы (рис. 12.76) видно, что при резонансе напряжение цепи U совпадает по фазе с током 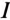
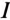
Колеблющаяся между магнитным полем индуктивности и электрическим полем емкости мощность (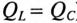
Из выражения (12.33) следует, что при отсутствии активной Мощности Р (активного сопротивления R) резонансный контур становится при резонансе идеальным колебательным контуром. Следовательно, при наличии активного сопротивления R источник расходует свою мощность на компенсацию потерь в контуре, за счет чего колебания в цепи будут незатухающими.
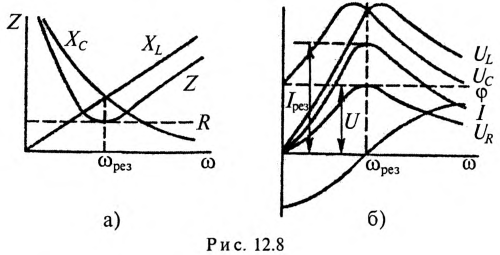
Кроме активного сопротивления R резонансной цепи и напряжения, приложенного к ней, все параметры резонансной цепи (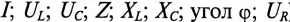
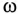
Эти изменения параметров резонансной цепи наглядно иллюстрируются резонансными кривыми, изображенными на рис. 12.8.
На резонансных кривых четко просматриваются значения этих параметров при частоте резонанса 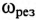
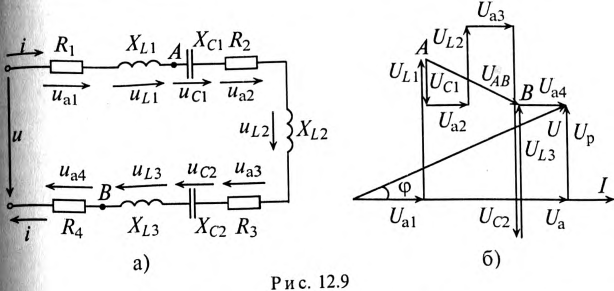
Общий случай неразветвленной цепи
Для неразветвленной цепи, содержащей несколько активных и реактивных сопротивлений различного характера (рис. 12.9а), справедливо геометрическое равенство напряжений (баланс напряжений)
которое лежит в основе построения векторной диаграммы (рис. 12.96).
Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи.
Из векторной диаграммы следует (рис. 12.96)
где 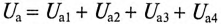
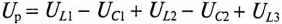
Те же рассуждения можно отнести и к сопротивлениям:
— полное сопротивление цепи 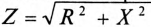
— активное сопротивление цепи 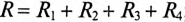
— реактивное сопротивление цепи
Напряжение на каком-либо участке неразветвленной цепи (рис. 12.9а), например на участке АВ, определяется так:_
Вектор напряжения UAB показан на векторной диаграмме (рис. 12.96).
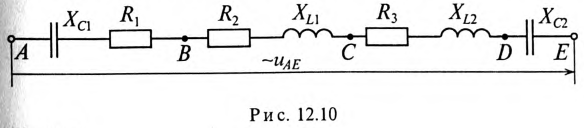
Пример 12.2
Напряжение, приложенное к неразветвленной цепи (рис. 12.10) U=220 В, частота тока сети f = 50 Гц. Начальная фаза тока 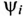
Сопротивление участков цепи: 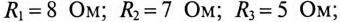
Требуется:
1. Вычислить ток цепи I и записать его мгновенное значение.
2. Записать мгновенное значение напряжения цепи иАЕ, определив предварительно угол ср и характер цепи.
3. Определить напряжение между точками АВ и CD.
4. Построить в масштабе векторную диаграмму цепи, определив едварительно напряжение на каждом сопротивлении.
5. Определить мощности S, Р и Q цепи.
6. Определить частоту, при которой в цепи наступит резонанс напряжений, и ток при резонансе.
7. Определить максимальную энергию, запасенную в магнитном поле катушек WmL и электрическом поле конденсаторов WmC. Как нужно изменить емкость конденсаторов, чтобы в цепи пил резонанс напряжений при частоте f = 50 Гц?
Решение
1. Для определения тока цепи I необходимо вычислить полное сопротивление цепи:
Действующее значение тока 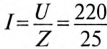
Угловая частота 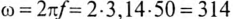
Мгновенное значение тока цепи:
2. Угол сдвига фаз ф и характер цепи определяется через tg ф:
Таким образом, угол ф = 37° (из таблицы), характер цепи индуктивный (+ф).
Тогда мгновенное значение напряжения цепи
где
3. Напряжение на участках:
4. Для построения векторной диаграммы определяются напряжения:
Векторная диаграмма цепи (отображает только характер участков, но не величины напряжений на них) изображена на рис. 12.11.
5. Полная мощность цепи 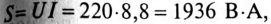
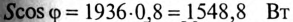
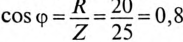
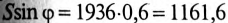
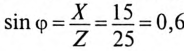
6. Для определения частоты резонанса вычисляется индуктивность L и емкость С цепи:
Тогда
Ток цепи при резонансе 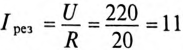
7. Максимальная энергия, запасенная в магнитном поле катушек:
Максимальная энергия, запасенная в электрическом поле конденсаторов:
8. Условие резонанса XL = XC.
По условию задачи 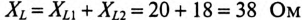
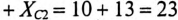
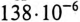
т. е. емкость конденсаторов нужно уменьшить на
Разветвленная цепь синусоидального тока
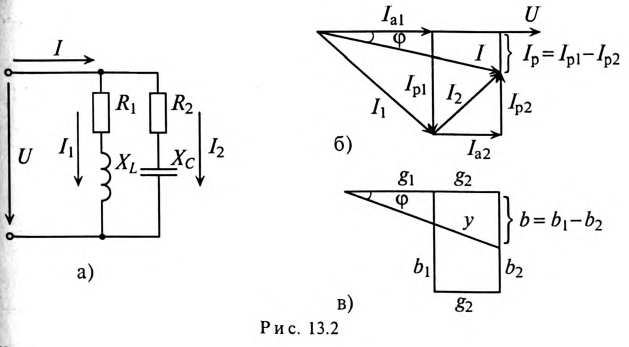
Активный и реактивный токи:
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
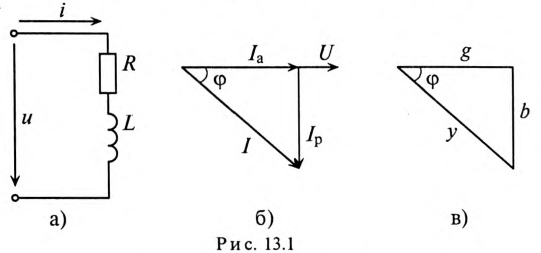
Если к цепи, содержащей активное сопротивление R и индуктивное XL (рис. 13.1а), приложено синусоидальное напряжение 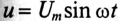
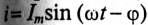
Векторная диаграмма в этом случае изображена на рис. 13.16.
Ток цепи I (рис. 13.16) раскладывается на две составляющие, одна из которых 



Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи (рис. 13.1а) ток на всех участках имеет одинаковое значение. Однако понятия активный 

13.2. Проводимости
Из треугольника токов для рассматриваемой цепи (рис. 13.16) следует: 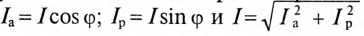
С другой стороны, известно, что 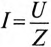
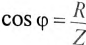
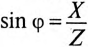
Тогда
где g — активная проводимость цепи, равная
Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.
А так как g определяет активный ток 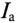
Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.
Величина реактивного тока определяется выражением
где b — реактивная проводимость цепи, равная
Величина полного тока цепи равна
где 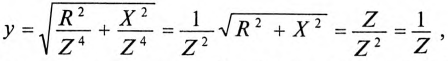
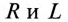
Таким образом, у — полная, или кажущаяся, проводимость цепи:
Полная (кажущаяся) проводимость цепи «у» является обратной величиной полного (кажущегося) сопротивления цепи.
Активная 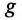
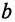
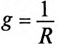
Если же в неразветвленной цепи (или ветви) включены сопротивления 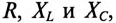
Параллельное соединение катушки и конденсатора
Если к источнику синусоидального напряжения 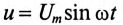
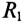
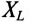
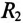
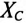
Действующие значения этих токов будут соответственно равны
Ток в неразветвленной цепи 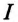
Для определения этого тока строится векторная диаграмма цепи (рис. 13.26), из которой следует:
где
Таким образом, ток в неразветвленной части цепи 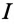
Реактивные проводимости в ветвях имеют различные знаки, так как сопротивления в ветвях различного характера (индуктивное и емкостное).
Треугольник проводимостей рассматриваемой цепи изображен на рис. 13.2в.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток цепи 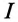
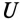
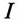
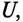
Резонанс токов
Резонанс токов в цепи (рис. 13.2а) с параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях:
Выражение (13.9) является условием резонанса токов в разветвленных цепях синусоидального тока. Полная (кажущаяся) проводимость при этом условии
так как
Таким образом, полная проводимость цепи при резонансе токов 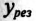
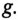
Реактивные токи в ветвях при резонансе токов равны между собой
Это равенство и определяет название «резонанс токов».
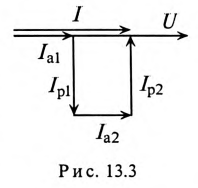
На основании равенства (13.12) строится векторная диаграмма при резонансе токов (рис. 13.3). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 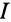
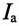
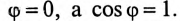
Эта активная мощность компенсирует потери на активном сопротивлении в параллельном резонансном контуре. Мощность (энергия), которая колеблется между электрическим полем конденсатора и магнитным полем индуктивности при резонансе, не является реактивной, так как не загружает источник и провода.
Частота резонанса токов в параллельном резонансном контуре может быть определена из условия резонанса токов, т. е. равенства реактивных проводимостей в ветвях
После ряда преобразований равенства (13.13) определяется частота резонанса токов
Резонансная частота зависит не только от параметров колебательного контура 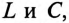
Если в резонансном контуре отсутствуют активные сопротивления в ветвях, то частота резонанса токов 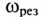
Если в резонансном контуре 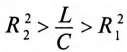
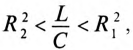
Резонанс токов нашел широкое применение в радиотехнике и выпрямительной технике (в резонансных фильтрах) и др.
Пример 13.1
Напряжение, приложенное к параллельно включенным катушке и конденсатору (рис. 13.4а), 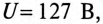
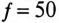
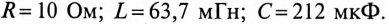
1) токи всех участков цепи:
2) углы сдвига фаз этих токов относительно напряжения:
3) полную S, активную Р и реактивную Q мощности цепи;
4) частоту, при которой наступит резонанс токов в этой цепи. Построить векторную диаграмму.
Решение
1. Сопротивление участков цепи:
где
Сопротивление 1-й ветви:
Токи в ветвях соответственно равны
Для определения тока 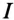
Тогда полная проводимость цепи будет равна
Ток в неразветвленной части цепи
2. Углы сдвига фаз:
.
Знак «минус» перед значением угла 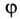
3. Полная мощность цепи
Активная мощность цепи 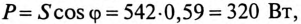
Реактивная мощность цепи 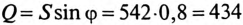
4. Угловая частота резонанса токов в цепи равна
Откуда
Для построения векторной диаграммы определяют активные и реактивные токи в ветвях:
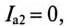
Векторная диаграмма для рассматриваемой цепи изображена на рис. 13.46.
На векторной диаграмме видно, что ток I опережает напряжение U на угол 53°30′ (цепь емкостного характера).
Коэффициент мощности
Номинальные параметры, т.е. мощность источника 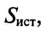
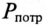
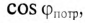
Из (13.15) следует, что чем меньше 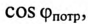
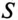
Ток в цепи потребителя с определенным 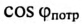
Из (13.16) видно, что чем меньше 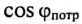
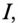
Таким образом, низкий коэффициент мощности потребителя 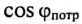

Однако 

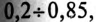
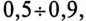
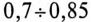
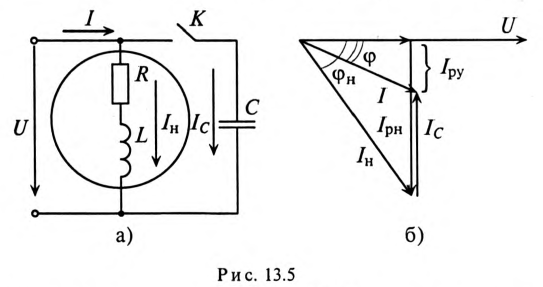
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения 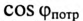
Из векторной диаграммы (рис. 13.56) видно, что с подключением конденсатора С (ключ К замкнут) появляется 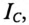
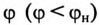
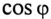
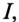
Для повышения коэффициента мощности 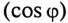
Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки).
Пример 13.2
Асинхронный двигатель, включенный в сеть с напряжением 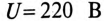
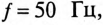
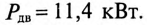
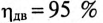
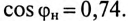
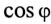
Решение
Мощность, потребляемая двигателем из сети:
Ток нагрузки 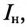
Реактивная составляющая тока двигателя 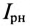
(по таблице 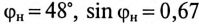
Ток установки 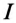
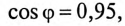
При 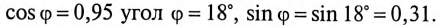
Ток конденсатора 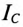
Емкостное сопротивление конденсаторов
Емкость конденсаторов, которые нужно подключить параллельно двигателю для улучшения 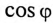
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле