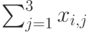Межотраслевые
поставки продукции xij
вычисляются по формуле
xij
= aij
xj ,
где aij
– элементы исходной матрицы А,
расположенной в ячейках А2:С4, xj
– элементы вектора Х, найденного выше
в п. 4 и расположенные в ячейках Е7:Е9.
Для проведения
вычислений xij
необходимо проделать следующее.
5.1. Вычислить
транспонированный вектор Хт
относительно вектора Х. При этом
вектор-столбец Х станет вектором-строкой
Хт.
Это необходимо для согласования
размерностей дальнейшего умножения
элементов векторов.
С этой целью:
— выделить указателем
мыши при нажатой левой кнопке ячейки
Е12:G12, в которых будет располагаться
транспонированный вектор Хт
;
— нажать на панели
инструментов кнопку Вставка,
а затем кнопку Функция.
В появившемся окне в поле Категория
выберите Ссылки
и массивы,
а в поле Выберите
функцию –
имя функции ТРАНСП
(рис. 3). Щелкните на кнопке ОК;
— появившееся
диалоговое окно ТРАНСП
мышью отодвиньте в сторону от исходного
вектора Х и введите диапазон вектора Х
(диапазон ячеек Е7:Е9) в рабочее поле
Массив
(протащив указатель мыши при нажатой
левой кнопке от ячейки Е7 до ячейки Е9);
— нажмите сочетание
клавиш Ctrl+Shift+Enter.
|
Рис. 3. Диалоговое ТРАНСП |
В результате в
поле ячеек Е12:G12 расположится
транспонированный вектор Хт
.
5.2. Вычислить
межотраслевые поставки продукции xij
. Для этого проделать следующие операции:
— поставить курсор
мыши в ячейку А22, в которой будет
расположено значение x11.
В этой ячейке набрать формулу =A2*E12,
которая означает, что x11
= a11
x1
.
— введенную формулу
скопируйте во все остальные ячейки
первой строки (в ячейки А22:С22, протащив
мышью крестик в правом нижнем углу от
ячейки А22 при нажатой левой кнопке мыши,
до ячейки С22. При этом будут вычислены
x12
= a12
x2
и x13
= a13
x3
.
Затем в ячейке А23
наберите формулу =A3*E12 и повторяя
аналогичную процедуру, получите значения
x21
= a21
x1
, x22
= a22
x2
и x23
= a23
x3
. Повторите аналогичные действия для
ячеек А24:С24.
В результате все
межотраслевые поставки продукции будут
найдены и расположатся в матрице с
ячейками А22:С24.
Тема 2. Экономико-математическая модель международной торговли (линейная модель обмена). Моделирование средствами Excel
Основные сведения
Рассмотрим бюджеты
n стран, которые обозначим как x1,
x2,
… , xn.
Предположим, что
национальный доход xj
страны j
затрачивается на закупку товаров внутри
страны и на импорт из других стран.
Обозначим через
xij
количество средств страны j расходуемое
на закупку товаров из страны i, при этом
xjj
– затраты на закупку товаров внутри
страны j. Тогда сумма всех затрат страны
j, идущее на закупку товаров как внутри
страны, так и на импорт из других стран
должна равняться национальному доходу
страны xj,
т.е.
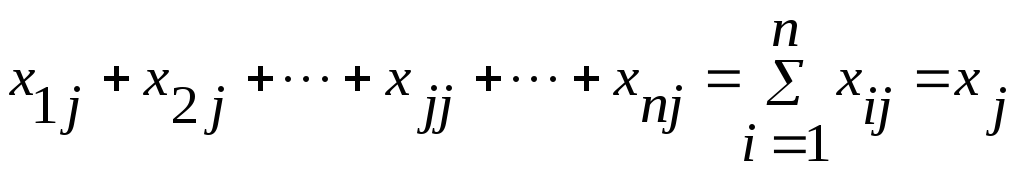
j
= 1, 2,…, n
. (4)
Разделив обе части
равенства (4) на xj
и введя коэффициенты
получим
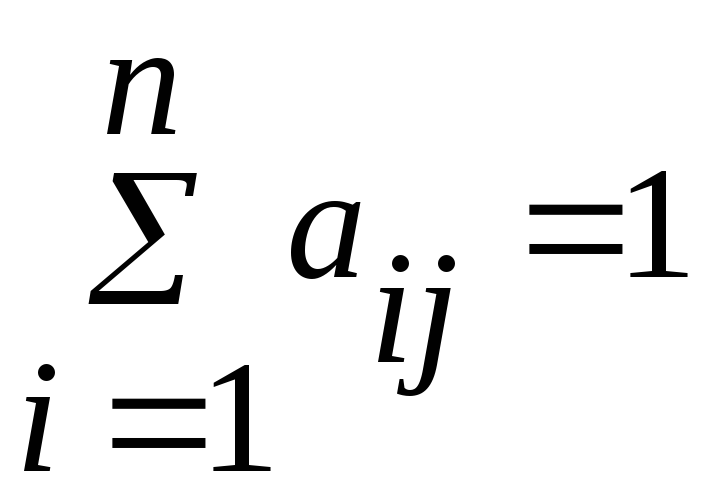
j
= 1, 2,…, n (5)
Коэффициенты
равны доли национального дохода страны
j расходуемую на закупку товаров у страны
i.
Матрица A коэффициентов
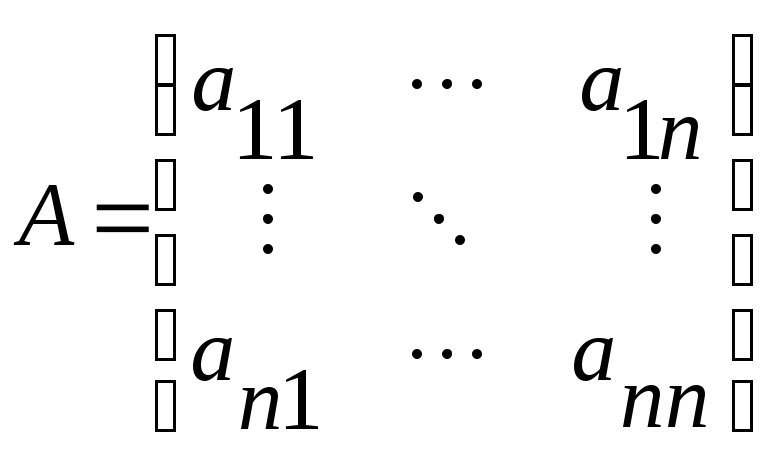
называется
структурной матрицей торговли. Понятно,
что сумма элементов каждого столбца
равна единице.
С другой стороны,
количество средств страны j расходуемое
на закупку товаров из страны i и равное
xij,
является выручкой для страны i за свой
товар, который у нее закупила страна j.
Суммарная выручка i-ой страны
равна

i
= 1, 2,…, n (7)
Так как
,
то
и равенство (7) можно записать в виде

i
= 1, 2,…, n
. (8)
Международная
торговля называется сбалансированной,
если сумма платежей (затрат) каждого
государства равна его суммарной выручке
от внешней и внутренней торговли.
В сбалансированной
системе международной торговли не
должно быть дефицита, другими словами,
у каждой страны выручка от торговли
должна быть не меньше ее национального
дохода, т.е.
,
i
= 1, 2,…, n
.
Одновременное
выполнение этих неравенств может иметь
место только в том случае, если
,
i
= 1, 2,…, n
, (9)
т.е. у всех торгующих
стран выручка от внешней и внутренней
торговли должна совпадать с национальным
доходом.
Равенства (9), с
использованием (8), можно записать в
матричном виде
AX
= X (10)
где А
– структурная матрица (6) международной
торговли; Х
– вектор национальных доходов стран

Матричное уравнение
(10) соответствует задаче на собственное
значение и собственный вектор матрицы
А.
Очевидно, что собственное значение
матрицы А,
согласно уравнению (10), равно 1, а
собственный вектор, соответствующий
этому собственному значению, равен Х.
Таким образом,
баланс в международной торговле
достигается тогда, когда собственное
значение структурной матрицы международной
торговли равно единице, а вектор
национальных доходов торгующих стран
является собственным вектором,
соответствующим этому единичному
собственному значении.
С помощью линейной
модели международной торговли можно,
зная структурную матрицу международной
торговли А
найти такие величины национальных
доходов торгующих стран (вектор Х),
чтобы международная торговля была
сбалансированной.
Моделирование
с использованием технологии Excel.
Определение
собственного вектора X
матрицы А
с помощью средств Microsoft
Excel невозможно.
Поэтому математическую
модель международной торговли сводят
к задаче линейного программирования.
Для этого, систему уравнений
(A
– E)X
= 0,
где Е
– единичная матрица
которая получается
из уравнений (10) переносом правой части
в левую, трактуют как ограничения-равенства.
Кроме того, вводят
новое ограничение-неравенство
,
отражающее условие,
по которому сумма бюджетов всех стран
должна быть не больше заданной величины
S.
В качестве целевой
функции вводится сумма бюджетов всех
стран, которая должна достигать максимума:
Итак, математическая
модель сбалансированной международной
торговли сводится к следующей
оптимизационной задаче линейного
программирования. Необходимо найти
максимум целевой функции
при ограничениях:
Пример с
использованием технологии Excel
Задача.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 7680 млн.ден.ед.
Математическая
модель
при ограничениях:
Решение задачи
средствами Excel
Методика решения
задачи линейного программирования с
помощью средств Поиска решения Excel
подробно рассматривалась в Лабораторной
работе №1 и поэтому здесь уже рассматриваться
не будет.
|
Рис. |
Задание исходных
данных на рабочем листе Excel приведено
на рис.4.
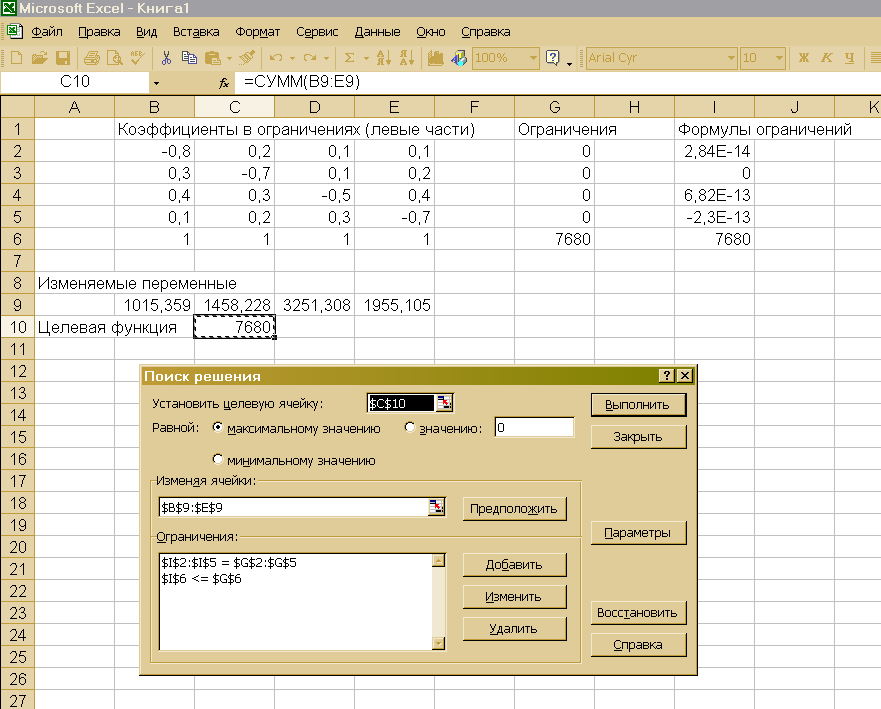
В ячейки В2:Е6
занесены коэффициенты при системе
ограничений, в ячейках G2:G6 содержатся
ограничения в правых частях, в ячейки
I2:I6 занесены формулы левых частей
ограничений, ячейки В9:Е9 содержат
изменяемые переменные
.
Например, в ячейке I2 записана формула
ограничений =СУММПРОИЗВ(В2:Е2;В9:Е9).
Аналогичные формулы записаны в ячейках
I3:I6. Формула целевой функции =СУММ(В9:Е9)
занесена в ячейку С10.
|
Рис. |
Процесс решения
– занесение в окно Поиск
решения ячейки с формулой
целевой функции, занесение изменяемых
ячеек, внесение ограничений приведено
на рис. 5. В окне Параметры необходимо
отметить: Линейная модель,
Неотрицательные значения,
Автоматическое
масштабирование.
На рис. 5 приведены
также результаты решения, согласно
которым национальные доходы четырех
стран
равны соответственно 1015.359, 1458.228, 3251.308,
1955.105 млн.ден.ед. Из содержимого ячеек
I2:I6 видно, что все ограничения выполнены.
Значение целевой функции (ячейка С10)
равно 7680 млн.ден.ед.
Индивидуальные
задания по Теме 1
Задание 1.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 2.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 3.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 4.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 5.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 6.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 7.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 8.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 9.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 10.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 11.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Задание 12.
Экономическая система состоит из трех
отраслей, для которых матрица прямых
затрат A и вектор конечного продукта Y
известны:

Определить: 1)
Матрицу коэффициентов полных материальных
затрат B. 2) Проверить продуктивность
матрицы A. 2) Вектор валового выпуска X.
3) Межотраслевые поставки продукции xij
Индивидуальные
задания по Теме 2
Задание 1.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 4590 млн.ден.ед.
Задание 2.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 15055 млн.ден.ед.
Задание 3.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 9000 млн.ден.ед.
Задание 4.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 59550 млн.ден.ед.
Задание 5.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 15590 млн.ден.ед.
Задание 6.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 51503 млн.ден.ед.
Задание 7.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 25590 млн.ден.ед.
Задание 8.
Найти национальные доходы
четырех торгующих стран в сбалансированной
системе международной торговли, если
структурная матрица торговли этих
четырех стран равна

а сумма бюджетов
стран не превышает 83355 млн.ден.ед.
Литература
1. Орлова И.В.
Экономико-математическое моделирование:
Практическое пособие по решению задач.
– М.: Вузовский учебник, 2004
3.2. Нахождение матрицы межотраслевых поставок и валовой продукции по матрице прямых затрат и вектору конечной продукции
Одна из основных задач межотраслевого баланса — найти при заданной структурной матрице 


Задача 3.1.
Рассмотрим — 3 сектора экономики ( промышленность, сельское хозяйство и транспорт).. В таблице приведены коэффициенты прямых затрат 

| Производящие отрасли | промышленность | Сельское хозяйство | Транспорт | Конечная продукция Y |
| Потребляющие отрасли | Коэфф. прямых затрат | |||
| промышленность | 0,1 | 0,05 | 0,2 | 155 |
| Сельское хозяйство | 0,3 | 0,00 | 0,15 | 25 |
| Транспорт | 0,2 | 0,4 | 0,00 | 20 |
| Чистая продукция V |
Найти:
- Матрицу межотраслевых поставок.
- Матрицу полных затрат
- Для каждой отрасли объем валовой продукции
- Определить объемы чистой продукции
- Выполнить проверку проведенных вычислений, заполнить матрицу МОБ.
Запишем необходимые уравнения:
Решение
Для расчета в Mathcad используем операции с матрицами и с индексными переменными .
Входные данные. Расчет валовой продукции.
Матрица прямых затрат:
Вектор конечной продукции:
Решение:
Вводим единичную матрицу
Матрица полных затрат 
Вектор объемов валовой продукции: 
Расчет матрицы межотраслевых поставок
-
Расчет через индексные переменные
— матрица межотраслевых поставок
-
Расчет через матрицы
С помощью функции
построим диагональную квадратную матрицу, элементы главной диагонали которой являются элементами полученного вектора продукции
.
,
— матрица межотраслевых поставок
Проверка проведенных вычислений. Расчет баланса в таблице МОБ.
Сумма по строкам (потребление отраслей):
Сумма по столбцам (производящие отрасли):
Вектор чистой продукции (Добавленная стоимость): 
Вектор валовой продукции:
- Авторы
- Файлы
- Ключевые слова
- Литература
Цысь Ю.В.
1
Долгополова А.Ф.
1
1 Ставропольский государственный аграрный университет
1. Высшая математика для экономистов: учебник / под ред. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2010.
2. Сирл С., Госман У. Матричная алгебра в экономике. – М.: Статистика, 1974.
3. Морозова О.В., Долгополова А.Ф., Долгих Е.В. Экономико-математические методы: теория и практика. – Ставрополь: СтГАУ «АГРУС», 2006.
В современной экономике используется множество математических методов, разработанных ещё в 20 веке. Применение линейной алгебры значительно упростило решение многих экономических задач. В данной работе рассматриваются основные способы решения задач с помощью элементов линейной алгебры.
Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют большое значение для экономистов, основная часть математических моделей экономических объектов и процессов записывается в простой и компактной матричной форме. С помощью матриц удобно описывать различные экономические закономерности. Например, дана следующая таблица средних розничных цен на автомобили в зависимости от срока их службы (условных единиц).
|
Продолжительность службы (годы) |
Годы |
||
|
2005 |
2006 |
2007 |
|
|
1 |
1881 |
2120 |
2445 |
|
2 |
1512 |
1676 |
1825 |
|
3 |
1261 |
1397 |
1484 |
|
4 |
1054 |
1144 |
1218 |
Предложенную таблицу можно записать в виде матрицы следующим образом:

где содержательное значение каждого показателя определяется его местом в матрице. К примеру, число 1825 во второй строке третьего столбца представляет собой цену прослужившего 2 года автомобиля в 2007 году. Аналогичным образом находим, что числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и тот же срок в различные годы, а числа в столбце – цены автомобилей различного срока службы в данном году.
Таким образом, место, занимаемое числом в матрице, характеризует продолжительность использования автомобиля и год, к которому относится цена.
Применение матриц при решении экономических задач рассмотрим на следующем примере. Предприятие выпускает продукцию трех видов P1, P2, P3 и использует сырье двух типов: S1, S2. Нормы расхода сырья характеризуются матрицей:
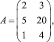
где каждый элемент aij (i = 1, 2, 3; j = 1,2) показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой C = (100 80 130).Стоимость единицы каждого типа сырья (денежных единиц) – матрицей-столбцом 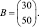
Решение: Затраты первого сырья составляют S1 = 2∙100 + 5∙80 + 1∙130 = 730единиц, а второго S2 = 3∙100 + 2∙80 + 4∙130 = 980 единиц. Значит затраты сырья S могут быть записаны в виде матрицы строки (730 980) и произведения:
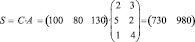
Общая стоимость сырья
Q = 730∙30 + 980∙50 = 70900 (денежных единиц)
может быть записана в следующем виде:
Q = S∙B = (CA)B = (70900).
Вывод: общая стоимость сырья составляет 70900.
Также экономические задачи можно решать с помощью систем линейных уравнений.
Рассмотрим и решим с помощью системы линейных уравнений следующую задачу:
Из определенного листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:
|
Тип заготовки |
Способ раскроя |
||
|
1 |
2 |
3 |
|
|
А |
3 |
2 |
1 |
|
Б |
1 |
6 |
2 |
|
В |
4 |
1 |
5 |
Записать в математической форме условия выполнения задания.
Решение: Обозначим через x, y, z количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тогда при первом способе раскроя x листов будет получено 3 заготовок типа А, при втором – 2y, при третьем – z. Для полного выполнения задания по заготовкам типа А должно выполняться равенство:
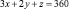
Таким же способом получаем уравнения:
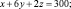
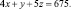
Имеем систему:
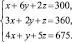
Данным уравнениям должны удовлетворять неизвестные x, y, z для того, чтобы выполнить задание по заготовкам Б и В. Полученная система линейных уравнений и выражает в математической форме условия выполнения всего задания по заготовкам А, Б и В.
Решим систему методом Гаусса.
1. Запишем систему в виде матрицы.
2. Составим расширенную матрицу системы.
3. Приведём полученную матрицу к треугольному виду.
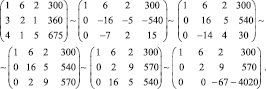
Исходная система равносильна следующей:
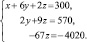
Решая полученную систему, имеем: x = 90, y = 15, z = 60.
Вывод: вектор C (90, 15, 60) есть решение системы.
Также, говоря, о роли линейной алгебры в экономике нельзя не упомянуть о модели многоотраслевой экономики Леонтьева, которая была разработана в виде математической модели в 1936 году. Эта модель основана на алгебре матриц и использует аппарат матричного анализа.
Рассмотрим задачу:
В таблице приведены коэффициенты прямых затрат и конечная продукция отраслей на плановый период, усл. ден. ед.
|
Отрасль |
Потребление |
Конечный продукт |
||
|
Промышленность |
Сельское хозяйство |
|||
|
Производство |
Промышленность |
0,3 |
0,2 |
300 |
|
Сельское хозяйство |
0,15 |
0,1 |
100 |
Найти: плановые объёмы валовой продукции отраслей, межотраслевые поставки, чистую продукцию отраслей.
Решение:
1. Выпишем матрицу коэффициентов прямых затрат A, вектор конечной продукции Y:
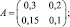
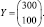
Заметим, что матрица A продуктивна, так как её элементы положительны и сумма элементов в каждом столбце меньше единицы.
2. Найдем матрицу
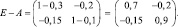
Тогда матрица полных затрат:
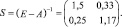
3. По формуле X = (E – A)–1⋅Y = SY найдем вектор валового продукта X:
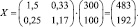
4. Межотраслевые поставки xij найдём по формуле xij = aij∙xj
X11 = a11∙x1 = 0,3·483 = 144,9;
X12 = 0,2·192 = 38,4;
X21 = 0,15·483 = 72,45;
X22 = 0,1·192 = 19,2.
5. Чистая продукция промышленности равна: 483 – 144,9 – 72,45 = 265,65
Чистая продукция сельского хозяйства: 192 – 38,4 – 19,2 = 134,4.
Итак, рассмотрев в данной статье некоторые задачи и их решения, можно сказать, что это лишь небольшая часть математических методов, используемых в экономике. Экономика и математика, очень тесно связаны и постепенно математические методы и модели начинают занимать очень важное место в экономике.
Библиографическая ссылка
Цысь Ю.В., Долгополова А.Ф. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И ИХ ПРИМЕНЕНИЕ ПРИ РЕШЕНИИ ЭКОНОМИЧЕСКИХ ЗАДАЧ // Современные наукоемкие технологии. – 2013. – № 6.
– С. 91-93;
URL: https://top-technologies.ru/ru/article/view?id=31998 (дата обращения: 26.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Задача
Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках
и векторе объемов конечного использования
.
Требуется:
Указание:
При вычислениях производить округление с точностью до тысячных.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Матрица прямых затрат
Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора
:
Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:
Подставляя
числовые значения, получаем:
Матрица «Затраты — выпуск»
Найдем матрицу
«Затраты — выпуск»
Вектор конечного использования Y для валового объема выпуска X
Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения:
Для этого выполним умножение двух матриц
Матрица полных затрат
Найдем
матрицу коэффициентов полных материальных затрат
-она будет равна обратной матрице
:
Определитель матрицы
:
Алгебраические
дополнения:
Обратная матрица:
Вектор валового объема выпуска X для конечного использования Y
Вектор валового объема выпуска
для конечного продукта
определим формуле:
Приросты валовых объемов выпуска
Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на
по сравнению с
:
Матрица полных затрат ресурсов S
Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:
Суммарная потребность в ресурсах
Суммарная потребность в ресурсах для вектора Y0:
Суммарная потребность в ресурсах для вектора Yn:
Матрицы косвенных затрат и сумма затрат
Найдем
матрицы косвенных затрат первого, второго и третьего порядка
Сумма затрат:
Разность
матриц:
Вектор потребности в продукции
Найдем
вектор потребности в продукции всех отраслей материального производства bij
для получения единицы конечного продукта bj вида. Для этого
просуммируем столбцы матрицы полных затрат:
Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.















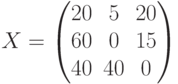 — матрица межотраслевых поставок
— матрица межотраслевых поставок построим диагональную квадратную матрицу, элементы главной диагонали которой являются элементами полученного вектора продукции
построим диагональную квадратную матрицу, элементы главной диагонали которой являются элементами полученного вектора продукции  ,
, 

 — матрица межотраслевых поставок
— матрица межотраслевых поставок