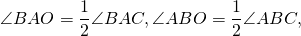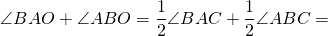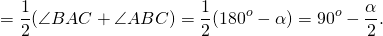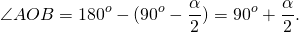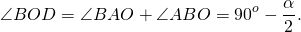Как найти угол между биссектрисами треугольника?
Задача.
В треугольнике ABC угол C равен α, AD и BE — биссектрисы, пересекающиеся в точке O.
Найти угол AOB.
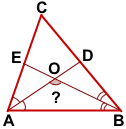
1) Так как сумма углов треугольника равна 180°, то в треугольнике ABC
∠BAC+∠ABC+∠C=180°, отсюда
∠BAC+∠ABC=180°-∠C,
∠BAC+∠ABC=180°-α.
2) Так как AD и BE — биссектрисы углов ∠BAC и ∠ABC, то
3) Для треугольника AOB
∠BAO+∠ABO+∠AOB=180°,
∠AOB=180°-(∠BAO+∠ABO),
Замечание.
В треугольнике AOB ∠BOD — внешний угол при вершине O. Следовательно,
Вывод:
Один уз углов, образованный при пересечении биссектрис двух углов треугольника, равен сумме 90° и половины третьего угла,
другой — разности 90° и половины третьего угла.
Запоминать для экзамена эти соотношения необязательно. Достаточно самостоятельно провести аналогичные рассуждения.
Решать данную задачу будем, основываясь на свойствах прямоугольного треугольника.
Вспомним некоторые эти свойства.
Нам в данном случае пригодится третье из списка свойство прямоугольного треугольника, а именно: медиана, проведенная к гипотенузе из прямого угла равна половине самой гипотенузы.
Посмотрим внимательно на чертеж и будем рассуждать так:
Визуально нам понятно, что наименьший угол прямоугольного треугольника расположен напротив меньшего катета. Угол А будет наименьшим.
Далее:
СД — биссектриса, значит она делит прямой угол пополам, и угол ДСА равен 45 градусам.
Можем узнать угол МСА — как разницу углов ДСА и ДСМ
45° — 14° = 31°
А теперь обратим внимание на свойство медианы и мы понимаем, что отрезки АМ и МС равные.
Если они равные, то треугольник АМС — равнобедренный с основанием АС
Тогда углы при основании у равнобедренного треугольника равны ( по свойству равнобедренного треугольника)
А раз так, то угол МСА, который мы нашли, что он равен 31 °, равен искомому углу САВ
Ответ:
Наименьший угол прямоугольного треугольника АВС равен 31°
Содержание
- Угол между биссектрисами треугольника
- Определение и свойства биссектрисы угла треугольника
- Определение биссектрисы угла треугольника
- Свойства биссектрисы треугольника
- Свойство 1 (теорема о биссектрисе)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Пример задачи
- Биссектриса угла
- Биссектриса угла — коротко о главном
- Определение биссектрисы угла
- Биссектриса равнобедренного треугольника
- Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике
- Читать далее…
- Биссектриса, медиана, высота — определения и отличия
- Угол между биссектрисами любого треугольника
Угол между биссектрисами треугольника
Как найти угол между биссектрисами треугольника?
В треугольнике ABC угол C равен α, AD и BE — биссектрисы, пересекающиеся в точке O.

1) Так как сумма углов треугольника равна 180°, то в треугольнике ABC
2) Так как AD и BE — биссектрисы углов ∠BAC и ∠ABC, то
3) Для треугольника AOB
В треугольнике AOB ∠BOD — внешний угол при вершине O. Следовательно,
Один уз углов, образованный при пересечении биссектрис двух углов треугольника, равен сумме 90° и половины третьего угла,
другой — разности 90° и половины третьего угла.
Запоминать для экзамена эти соотношения необязательно. Достаточно самостоятельно провести аналогичные рассуждения.
Источник
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
Источник
Биссектриса угла
Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы угла треугольников и других фигур.
Эти знания сильно упростили жизнь людей. Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек…
Нам же знание этих свойств поможет решить некоторые задания ЕГЭ!
Биссектриса угла — коротко о главном
Биссектриса угла — это линия, делящая угол пополам.
Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Теорема 1. Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.
Теорема 2. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
Теорема 3. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.
Теорема 4. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
Теорема 5. Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.
Теорема 6. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.
А теперь подробнее…
Определение биссектрисы угла
Помнишь шутку: «Биссектриса это крыса, которая бегает по углам и делит угол пополам»?
Так вот, настоящее определение биссектрисы угла очень похоже на эту шутку — биссектриса действительно делит пополам угол (а не отрезок, например):
Биссектриса угла – это линия, делящая угол пополам.
Или еще вот такое определение биссектрисы:
Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.
А вот определение биссектрисы треугольника:
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.
Биссектриса равнобедренного треугольника
Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой.
Но представляешь, это ещё не всё. Верна ещё и обратная теорема:
Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.
Мы скоро докажем обе этих теоремы, а пока твердо запомни:
Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!
Зачем же это твердо запоминать? Как это может помочь?
А вот представь, что у тебя задача:
Дано: ( AB=5,
Найти: ( displaystyle BC. )
Ты тут же соображаешь, (displaystyle BD ) биссектриса и, о чудо, она разделила сторону ( displaystyle AC ) пополам! (по условию…).
Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что AB=BC и значит, пишешь ответ: BC=5.
Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!
Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике
Почему в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?
Как это доказать?
Смотри: у ( triangle ABL ) и ( triangle CBL ) равны стороны ( AB ) и ( BC ), сторона ( BL ) у них вообще общая и ( angle 1=angle 2). (( BL ) – биссектриса!)
И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.
Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что ( triangle ABL=triangle CBL ), а значит ( AL )= ( CL ) и ( angle 3=angle 4 ).
( AL ) = ( CL ) – это уже хорошо – значит, ( BL ) оказалась медианой.
А вот что такое ( angle 3=angle 4 )?
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Будет немного сложнее, но пока мы отвлечемся на термины — повторим что такое биссектриса, медиана и высота, чем они похожи и чем они отличаются.
Кстати, а помнишь ли ты все эти термины? Чем они отличаются друг от друга?
Если нет, не страшно. Сейчас разберемся.
- Основание равнобедренного треугольника – это та сторона, которая не равна никакой другой. Посмотри на рисунок, как ты думаешь, какая это сторона? Правильно – это сторона ( AC. );
- Медиана – это линия, проведенная из вершины треугольника и делящая противоположную сторону (это снова ( AC ) пополам. Заметь, мы не говорим: «Медиана равнобедренного треугольника». А знаешь почему? Потому что медиана, проведенная из вершины треугольника, делит противоположную сторону пополам в ЛЮБОМ треугольнике.;
- Высота – это линия, проведенная из вершины и перпендикулярная основанию. Ты заметил? Мы опять говорим о любом треугольнике, а не только о равнобедренном. Высота в ЛЮБОМ треугольнике всегда перпендикулярна основанию.
Чем биссектриса, медиана и высота похожи между собой?
Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.
Чем биссектриса, медиана и высота отличаются между собой?
- Биссектриса делит угол, из которого выходит, пополам.
- Медиана делит противоположную сторону пополам.
- Высота всегда перпендикулярна противоположной стороне.
Вернемся к нашим баранам — к свойствам биссектрисы…
Угол между биссектрисами любого треугольника
B ( triangle ABC )проведем две биссектрисы ( AO )и ( OC ).
Они пересеклись. Какой же угол получился у точки ( O )?
Давай его посчитаем. Ты помнишь, что сумма углов треугольника равна ( 180<>^circ ) ?
Применим этот потрясающий факт. С одной стороны, из ( triangle ABC ):
( angle A+angle B+angle C=180<>^circ ), то есть ( angle B=180<>^circ text< >-text< >left( angle A+angle C right) ).
Теперь посмотрим на ( triangle AOC ):
( angle 2+angle 6+angle 3=180<>^circ )
Но биссектрисы, биссектрисы же!
Значит ( left( triangle AOC right) )
Вспомним про ( triangle ABC : angle A+angle C=180<>^circ -angle B )
Значит, ( angle 6=180<>^circ -frac<180<>^circ -angle B><2>=90+frac<angle B> <2>)
Теперь через буквы
Не удивительно ли?
Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!
Ну вот, две биссектрисы мы посмотрели. А что, если их три?! Пересекутся ли они все в одной точке?
Источник

Alex
Меньший 58 градусов:
——————————————————————-
угол B+угол C= 180-64=116 биссектрисы делят их пополам, значит угол B/2+угол C/2=116/2=58
угол между биссектрисами = 180-58=122 и смежный с ним 180-122=58
меньший 58
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 88 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Острый угол B прямоугольного треугольника ABC равен 61°. Найдите угол между высотой CH и биссектрисой CD, проведёнными из вершины прямого угла. Ответ дайте в градусах.
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21°. Найдите меньший угол данного треугольника. Ответ дайте в градусах.
Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах.
В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
Один из углов прямоугольного треугольника равен
°. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
Дана окружность радиуса 4 с центром в точке О, расположенной на биссектрисе угла, равного 60°. Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности внешним образом, если известно, что расстояние от точки О до вершины угла равно 10.
Расстояние между параллельными прямыми равно 6. На одной из них лежит вершина C, на другой — основание AB равнобедренного треугольника ABC. Известно, что AB = 16. Найдите расстояние между центрами окружностей, одна из которых вписана в треугольник ABC, а вторая касается данных параллельных прямых и боковой стороны треугольника ABC.
В правильной треугольной призме ABCA1B1C1 стороны основания равны 2, боковые ребра равны 3, точка D — середина ребра CC1.
а) Докажите, что плоскость делит объем призмы пополам.
б) Найдите угол между плоскостями ABC и ADB1.
В правильной треугольной призме ABCA1B1C1 стороны основания равны 1, боковые ребра равны 2, точка D — середина ребра CC1.
а) Докажите, что плоскость делит объем призмы пополам.
б) Найдите угол между плоскостями ABC и ADB1.
Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E. Окружность, описанная около треугольника ADE, пересекает прямую AC в точке F, отличной от A. Найдите радиус окружности, описанной около треугольника ABC, если AC = 6, AF = 3, угол BAC равен 45°.
Острые углы прямоугольного треугольника равны 85° и 5°. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Вневписанной окружностью треугольника называется окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон. Радиусы двух вневписанных окружностей прямоугольного треугольника равны 7 и 17. Найдите расстояние между их центрами.
Расстояние между параллельными прямыми равно 12. На одной из них лежит вершина C, на другой — основание AB равнобедренного треугольника ABC. Известно, что AB = 10. Найдите расстояние между центрами окружностей, одна из которых вписана в треугольник ABC, а вторая касается данных параллельных прямых и боковой стороны треугольника ABC.
Всего: 88 1–20 | 21–40 | 41–60 | 61–80 …