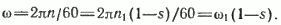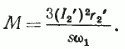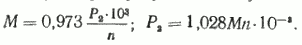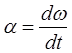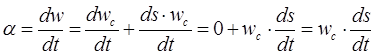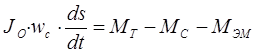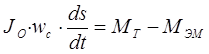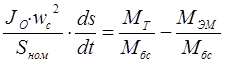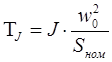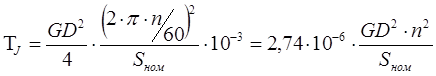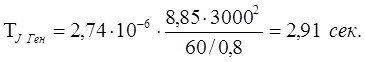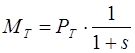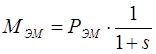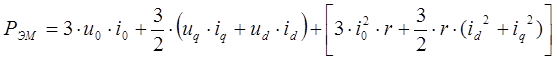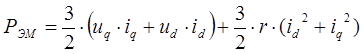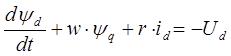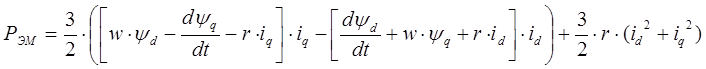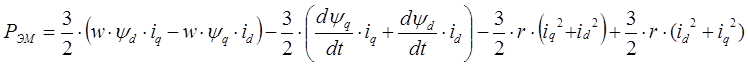Министерство
образования и науки Российской федерации
Федеральное
агентство по образованию
Саратовский
государственный технический университет
Балаковский
институт, техники, технологии и управления
РАСЧЕТ ХАРАКТЕРИСТИК ДВИГАТЕЛЕЙ
ПОСТОЯННОГО ТОКА
Методические
указания к выполнению практической
работы
по
дисциплине «Электромеханические
системы» для студентов
специальности
210100 всех форм обучения
Одобрено
редакционно-издательским
советом
Балаковского
института техники,
технологии
и управления
Балаково 2009
Цель работы: Изучить способы расчета
механических характеристик двигателя
постоянного тока независимого и
последовательного возбуждения.
РАСЧЕТ МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ДПТ
НЕЗАВИСИМОГО ВОЗБУЖДЕНИЯ
Расчет механических характеристик
электроприводов с ДПТНВ в основном
режиме. Механические характеристики –
зависимость частоты вращения n
или угловой скорости ω от электромагнитного
момента двигателя n=f(M)
или ω=f(M)
при неизменных значениях других
параметров, способных влиять на частоту
вращения и величину момента двигателя
(напряжение питания, величины тока и
так далее).
Рис.1. Схема двигателя
постоянного тока
Без учета индуктивности якорной цепи
Следует что
Электромагнитный момент
-
,
Тогда
где ω0 — скорость идеального
холостого хода;
Δω — изменение угловой скорости
относительно скорости холостого хода,
вызванное изменением нагрузки двигателя
(момента на его валу).
Все механические характеристики ДПТНВ
пересекаются в точках ω0.
Регулирование частоты вращения ДПТНВ
осуществляется:
— изменением сопротивления реостата
rдоб в цепи якоря
(только в сторону ее уменьшения от
номинальной)
— изменением магнитного потока возбуждения
с помощью реостата Ф в цепи обмотки
возбуждения (при двухзонном регулировании)
— изменением подводимого к цепи якоря
напряжения (только в низ от номинальной
частоты вращения, так как подавать на
двигатель напряжение выше номинального
недопустимо по условиям коммутации и
электрической прочности изоляции).
— импульсное регулирование (цепь якоря
периодически подключается к сети). Если
же хотя бы один из перечисленных
параметров двигателя изменен, то
механические характеристики называются
искусственными.
Для ДПТ – механические характеристики
прямолинейны и определяются двумя
точками:
Точка А – точка холостого хода ω = ω0,
M=0.
Точка Б – соответствующая номинальной
нагрузке двигателя с координатами MНОМ
и ωНОМ.
Для естественной характеристики точка
Б определяется из каталога
-
;
.
Для точки А скорость холостого хода
-
;
.
Для построения искусственной характеристики
точки Б рассчитывается число оборотов
-
.
1 – естественная
характеристика при rдоб1=0
2; 3 – искусственные
характеристики при rдоб1>0
rдоб2>0,
и при rдоб3>rдоб4
Рис.2. Естественная
и искусственные механические характеристики
При расчете механических характеристик
обычно решают одну из двух задач:
-
По заданным координатам точки на
искусственной механической характеристики
при номинальной нагрузке с координатами
MНОМ и nНОМ
определяют сопротивление резистора
M, в соответствующее этой
искусственной характеристики. -
По заданным значениям сопротивления
резистора M и тока якоря
IЯНОМ, соответствующего
номинальной нагрузке двигателя,
определяют частоту вращения якоря
двигателя и строят искусственную
механическую характеристику.
Задача 1: ДПТНВ имеет номинальные
данные:
— мощность РНОМ=42кВт;
— напряжение UНОМ=440В;
— частота вращения nНОМ=3000об/мин;
— сопротивление обмоток цепи якоря
RЯ=0,17Ом;
— КПД ηНОМ=90,5%.
Требуется определить сопротивление
резистора rдоб,
который следует включить последовательно
в цепь якоря, чтобы при номинальном
моменте нагрузки MНОМ
частота вращения была n’НОМ=0,5
nНОМ об/мин.
Решение:
-
Ток якоря в номинальном режиме:
-
Пограничная частота вращения:
-
Номинальный момент на валу двигателя:
-
Координаты точки номинального режима
на естественной механической
характеристики:;
.
-
Номинальное сопротивление двигателя:
-
Сопротивление резистора M,
соответствует искусственной механической
характеристике с координатой частоты
вращения: -
Механические характеристики ЭП с
рассматриваемым двигателем на рис.3:
Рис.3. Естественная
и искусственная механические характеристики
Н
рис.3 цифрой 1 обозначена естественная
характеристика, а цифрой 2 искусственная
характеристика. В режиме искусственной
механической характеристики вводится
понятие номинального сопротивления,
представляющего собой сопротивление
RНОМ, каким должна
обладать цепь якоря двигателя, чтобы
при подведенном к неподвижному якорю
напряжении UНОМ ток
в цепи якоря был бы номинальным IЯНОМ:
Задача 2: Рассчитать координаты
необходимые для построения естественной
и искусственной механической характеристики
ДПТНВ типа ПБС-62, если внешнее сопротивление
в цепи якоря rдоб=2,4Ом.
Номинальные данные двигателя:
— мощность РНОМ=4,7кВт;
— напряжение UНОМ=220В;
— частота вращения nНОМ=1000
об/мин;
— КПД ηНОМ=87%.
Решение:
-
Номинальный ток якоря:
-
Номинальное сопротивление двигателя:
-
Сопротивление обмоток в цепи якоря:
-
Пограничная частота вращения:
-
Номинальный момент:
-
Частота вращения в режиме искусственной
механической характеристики при
номинальном моменте нагрузки:
7) По координатам n0=1069об/мин,
nНОМ=1000 об/мин и
MНОМ=44,9Н·м строят
естественную механическую характеристику;
а по координатам n0=1069об/мин,
n’НОМ=714 об/мин и
MНОМ=44,9Н·м, строят
искусственную механическую характеристику.
РАСЧЕТ МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ДПТ
ПОСЛЕДОВАТЕЛЬНОГО ВОЗБУЖДЕНИЯ
На рис.4 представлена схема включения
ДПТ последовательного возбуждения.
Рис.4. Схема ДПТ
последовательного возбуждения
Отличительный признак – ток нагрузки
двигателя (ток якоря) является током
возбуждения IЯ=IB=I,
поэтому магнитный поток Ф зависит от
нагрузки:
-
,
где С – коэффициент пропорциональности.
При том вращающий момент
-
,
то есть пропорционален квадрату тока,
тогда ток
-
.
Число оборотов:
-
,
следовательно механическая характеристика
ДПТ криволинейна.
Особенности характеристики:
-
Механическая характеристика не
пересекает ось координат, так как при
отсутствии нагрузки двигателя частота
вращения возрастает неограниченно. По
той причине не допускается работа ДПТПВ
при нагрузке M≤0?25MНОМ. -
При малых нагрузках частота вращения
значительна (характеристика мягкая).
При нагрузках близких к номинальной,
характеристика становится более жесткой
(пологой). Объясняется это тем, что при
токе нагрузки IЯ≥0,8IЯНОМ
магнитная система насыщается и магнитный
поток возбуждения остается практически
неизменным.
Для построения естественной механической
характеристики n=f(M)
ДПТПВ по универсальным характеристикам
поступают следующим образом:
1) Определяют фактические номинальные
значения тока IЯ(A),
момента M(Н·м) и частоты
вращения n об/мин.
2) Задаются рядом относительных значений
тока нагрузки и по универсальной
характеристики определяют относительные
значения момента М* и частоты n*
3) Сроят естественную механическую
характеристику, пересчитав через
номинальное и относительное значения
требуемых параметров с целью определения
текущих.
Задача 3: Построить естественную
механическую характеристику для ДПТПВ
с техническими данными:
— IЯНОМ=19A;
— PНОМ=3кВт;
— UНОМ=220B;
— nНОМ=1130 об/мин.
Решение:
-
Номинальное значение момента
2) По полученным данным строим естественную
механическую характеристику (график
проходящий через точку А1)
При расчете искусственных характеристик
решают так же одну из двух задач:
-
Либо по заданным координатам точки на
искусственной механической характеристики
определяют сопротивление резистора
rдоб, необходимое
для получения требуемой искомой
характеристики. -
Либо по заданным сопротивлениям rдоб
определяют координаты точек искусственной
характеристики.
3) Задаемся относительными значениями
тока нагрузки и по универсальным
естественным характеристикам определяем
величины, необходимые для построения
естественной характеристики двигателя
сначала в относительных единицах, затем
в именованных.
Рис.5. универсальная
естественная характеристика
Рис.6. График
естественной и искусственных механических
характеристик
Задача 4: Для двигателя последовательного
возбуждения (см задача выше) определить
сопротивление резистора rдоб,
при включении которого в цепь якоря
искусственная механическая характеристика
пройдет через т А2 с координатами:
MНОМ=25,35Н·м, nНОМ=750
об/мин.
Решение:
-
Номинальное сопротивление двигателя:
-
КПД в номинальном режиме:
-
Сопротивление обмоток в цепи якоря:
-
Сопротивление резистора rдоб
ВАРИАНТЫ ЗАДАНИЙ
Для всех задач использовать формулировку
как в приведенных примерах. Технические
характеристики двигателей выбрать из
таблицы согласно вариантам.
Таблица 1 –
Технические характеристики двигателей
|
№ |
РН, |
Uн, |
КПД, |
nH, |
RЯЦ, |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
4 |
220 |
72.3 |
900 |
4.06 |
|
2 |
3.45 |
220 |
69.3 |
750 |
5.96 |
|
3 |
2 |
220 |
57.6 |
450 |
9.33 |
|
4 |
4.25 |
220 |
68 |
730 |
4.57 |
|
5 |
3 |
220 |
60.3 |
475 |
7.24 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
3.55 |
220 |
60.1 |
425 |
6.62 |
|
7 |
15 |
220 |
77.9 |
1400 |
0.278 |
|
8 |
7.5 |
220 |
76 |
1000 |
1.93 |
|
9 |
6 |
220 |
74 |
875 |
3.09 |
|
10 |
4.25 |
220 |
65 |
580 |
4.79 |
|
11 |
11 |
220 |
78.5 |
1060 |
1.23 |
|
12 |
8.5 |
220 |
76 |
875 |
2.08 |
|
13 |
8 |
220 |
68 |
600 |
2.93 |
|
14 |
11 |
220 |
76 |
800 |
1.77 |
|
15 |
8.5 |
220 |
68 |
515 |
2.76 |
|
16 |
15 |
220 |
80.7 |
850 |
1.31 |
|
17 |
11 |
220 |
70.5 |
530 |
2.23 |
|
18 |
15 |
220 |
75.3 |
580 |
1.65 |
|
19 |
17 |
220 |
73 |
500 |
1.53 |
|
20 |
20 |
220 |
75 |
475 |
1.36 |
ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ
1. Подготовка к работе – 1,0 акад.час
2. Выполнение работы – 2,0 акад.часа
3. Оформление работы – 1,0 акад.час
ЛИТЕРАТУРА
-
Кацман М.М. Электрический привод: Учебник
для студ. образоват. учреждений сред.
проф. образования. – М.: Издательский
центр «Академия», 2005. – 384с. ISBN
5-7695-2060-4 -
Практикум по электротехнике и электронике.
Учебное пособие для вузов / Кононенко
В.В., Мишкович В.И., Муханов В.В., Планидин
В.Ф., Чеголин П.М. / Под ред. В.В.Кононеко.
– Ростов н/Д. Феникс, 2007. – 384с.
СОДЕРЖАНИЕ
Введение 2
Расчет механических характеристик ДПТ
независимого возбуждения 2
Расчет механических характеристик ДПТ
последовательного
возбуждения 8
Варианты заданий 12
Время, отведенное на выполнение
работы 13
Литература 13
РАСЧЕТ ХАРАКТЕРИСТИК ДВИГАТЕЛЕЙ
ПОСТОЯННОГО ТОКА
Методические
указания к выполнению практической
работы по
дисциплине
«Электромеханические системы» для
студентов
специальности
210100 всех форм обучения
Составили:
Мефедова Юлия Александровна
Рецензент
Т.Н. Скоробогатова
Редактор Л.В.Максимова
Корректор А.М.Рогачева
|
Подписано |
Формат 60х84 |
|
|
Бумага |
Усл. печ. л. |
Уч.-изд.л. |
|
Тираж 100 |
Заказ |
Бесплатно |
Саратовский государственный технический
университет
410054, г.Саратов, ул.Политехническая, 77
Копипринтер БИТТиУ, 413840, г.Балаково, ул.
Чапаева, 140
16
Основные уравнения двигателя постоянного тока (ДПТ)
В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Ток якоря Iя
Выразим из формулы 2 ток якоря.
Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.
Электромагнитная мощность двигателя
Электромагнитный момент
где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)
Момент на валу двигателя, т.е. полезный момент, где М0 момент холостого хода;
Электродвигатель постоянного тока
Основные параметры электродвигателя постоянного тока
Постоянная момента

- где M — момент электродвигателя, Нм,
– постоянная момента, Н∙м/А,
- I — сила тока, А
Постоянная ЭДС
Направление ЭДС определяется по правилу правой руки. Направление наводимой ЭДС противоположно направлению протекающего в проводнике тока.
Наведенная ЭДС последовательно изменяется по направлению из-за перемещения проводников в магнитном поле. Суммарная ЭДС, равная сумме ЭДС в каждой катушке, прикладывается к внешним выводам двигателя. Это и есть противо-ЭДС. Направление противо-ЭДС противоположно приложенному к двигателю напряжению. Значение противо-ЭДС пропорционально частоте вращения и определяется из следующего выражения: [1]

Постоянные момента и ЭДС в точности равны между собой KT = KE. Постоянные KT и KE равны друг другу, если они определены в единой системе едениц.
Постоянная электродвигателя
Одним из основных параметров электродвигателя постоянного тока является постоянная электродвигателя Kм. Постоянная электродвигателя определяет способность электродвигателя преобразовывать электрическую энергию в механическую.

Постоянная электродвигателя не зависит от соединения обмоток, при условии, что используется один и тот же материал проводника. Например, обмотка двигателя с 6 ветками и 2 параллельными проводами вместо 12 одиночных проводов удвоят постоянную ЭДС, при этом постоянная электродвигателя останется не изменой.
Жесткость механической характеристики двигателя

- где
— жесткость механической характеристики электродвигателя постоянного тока
Напряжение электродвигателя
Уравнение баланса напряжений на зажимах двигателя постоянного тока имеет вид (в случае коллекторного двигателя не учитывается падение напряжения в щеточно-коллекторном узле):

Уравнение напряжения выраженное через момент двигателя будет выглядеть следующим образом:
Соотношение между моментом и частотой вращения при двух различных напряжениях питания двигателя постоянного тока неизменно. При увеличении частоты вращения момент линейно уменьшается. Наклон этой функции KTKE/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.
Благодаря таким характеристикам упрощается управление частотой вращения и углом поворота двигателей постоянного тока. Это характерно для коллекторных и вентильных двигателей постоянного тока, что нельзя сказать о двигателях переменного тока и шаговых двигателях [1].
Мощность электродвигателя постоянного тока
Упрощенная модель электродвигателя выглядит следующим образом:
- где I – сила тока, А
- U — напряжение, В,
- M — момент электродвигателя, Н∙м
- R — сопротивление токопроводящих элементов, Ом,
- L — индуктивность, Гн,
- Pэл — электрическая мощность (подведенная), Вт
- Pмех — механическая мощность (полезная), Вт
- Pтеп — тепловые потери, Вт
- Pинд — мощность затрачиваемая на заряд катушки индуктивности, Вт
- Pтр — потери на трение, Вт
Механическая постоянная времени
Механическая постоянная времени — это время, отсчитываемое с момента подачи постоянного напряжения на электродвигатель, за которое частота вращения ненагруженного электродвигателя достигает уровня в 63,21% (1-1/e) от своего конечного значения.

- где
— механическая постоянная времени, с
Баланс мощностей электрической цепи
Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.
Определение
Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.
Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.
Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:
Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.
Назначение
Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.
Переменный ток
Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.
- Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
- Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
- Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.
Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.
Постоянный ток
В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.
- В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
- I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
- Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
- Pист=I×E=1×10=10 Ватт. Это значение для источника.
- Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
- Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.
При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.
Заключение
В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.
Видео по теме
http://engineering-solutions.ru/motorcontrol/dcmotor/
http://profazu.ru/knowledge/electrical/balans-moshhnostej.html
Главная / Техническая информация / Механические характеристики асинхронного двигателя
Механические характеристики асинхронного двигателя — зависимость частоты вращения ротора от нагрузки (вращающегося момента на валу).
Электромагнитный момент М, развиваемый асинхронным двигателем, можно определять двумя способами: через электромагнитную мощность Рэм и через полную механическую мощность двигателя Р2:
М=Р2‘/ω, (39)
где Р2 —полная механическая мощность, Вт; ω=2πn/60 — механическая угловая скорость вращения ротора, 1/с; n — частота вращения ротора, об/мин.
Скорость ω связана с синхронной ω1 соотношением
Подставляя выражение для ω и Р2‘ по уравнению (36) в уравнение (39), получаем
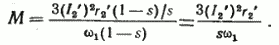
Выражение для момента через электромагнитную мощность имеет вид
М=Рэм/ω1,
Значение Рэм находится по уравнению (35), после чего представляем
Таким образом мы получим тождественное выражение для момента. Поскольку независимой величиной является не ток, а приложенное напряжение, то для получения окончательного выражения момента подставим в (40) значение тока I2‘ по уравнению (32):
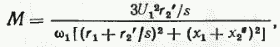
где М — момент, Н∙м; ω1 — синхронная скорость, с-1; U1 — напряжение, В; r1, r2‘, x1, x2‘ —сопротивления, Ом; s — скольжение, отн. ед.
Если необходимо иметь значение момента во внесистемных единицах — в килограммах силы-метрах, то полученный по (41) результат следует разделить на 9,81.
При эксплуатации часто необходимо определять момент по известной механической мощности Р2 (кВт) и частоте вращения n (об/мин). В этом случае формула (39) имеет вид, Н/м,
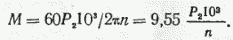
Отсюда мощность Р2 связана с моментом и частотой вращения соотношением
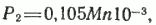
где М — момент, Н∙м; n — частота вращения, об/мин.
Если момент выражен в килограммах силы-метрах, то формулы (42), (43) преобразуются к виду
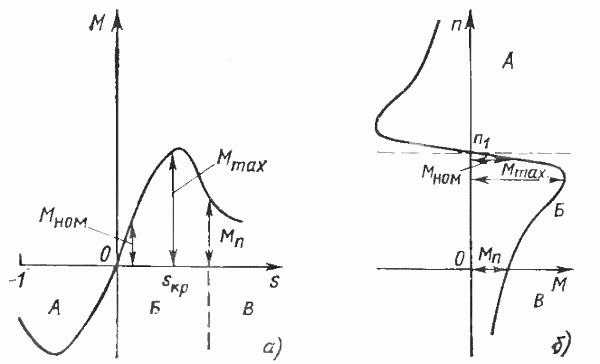
Зависимость между моментом и скольжением (41) при постоянном напряжении U1 и частоте f1 сети называется механической характеристикой. Естественная механическая характеристика асинхронного двигателя приведена на рис. 20. Там же приведена механическая характеристика M=f (n), часто встречающаяся на практике и полученная из характеристики M = φ(s) пересчетом (s=0 соответствует синхронной частоте вращения n1, s =1-n=0 и т. д.).
Рис. 20. Естественная механическая характеристика асинхронного двигателя: a —M=f(s); б – n =f(М); А—генераторный режим; Б — режим двигателя; В — режим электромагнитного тормоза
Используя формулу (41), можно получить достаточно полное представление о механических характеристиках асинхронного двигателя. Обратим прежде всего внимание на то, что механический момент двигателя зависит от трех групп величин: во-первых, это величины, определяемые конструкцией двигателя, к их числу относятся r1 и r’2, x1, х’2; во-вторых, величины, характеризующие напряжение, подводимое к двигателю, — напряжение на его зажимах U и частота питающего напряжения f (так как ω1 = 2πf); наконец, последняя величина, определяющая момент, развиваемый двигателем, зависит от режима его работы — это скольжение s.
Рассмотрим физические явления, обусловливающие такую форму механической характеристики. При частоте вращения ротора, равной синхронной, проводники ротора движутся с той же скоростью, что и вращающееся магнитное поле. Поэтому ЭДС, а следовательно, и ток в роторе равны нулю. Поэтому равен нулю и вращающий момент двигателя. При уменьшении частоты вращения ротора ниже синхронной проводники обмотки ротора начинают пересекать магнитное поле машины, в результате чего в обмотке ротора наводится ЭДС, пропорциональная скольжению ротора [см. формулу (14)]. При малых скольжениях (в пределах от s=0 до s=sкр) ток ротора также изменяется почти пропорционально скольжению. К такому выводу можно прийти, рассматривая уравнение (25) или (32). Так, в уравнении (25) при малых значениях s можно пренебречь составляющей sx2 в знаменателе по сравнению со значением r2, а в (32) можно пренебречь всеми составляющими в знаменателе по сравнению со значением r’2/s.
Таким образом, ток ротора в этом диапазоне скольжений практически определяется величиной ЭДС ротора, деленной на постоянное активное сопротивление r2 [уравнение (25)].
Как видно из рис. 20, механическая характеристика в зоне малых скольжений s<sкр линейна. В этой же области скольжений находится и номинальное скольжение sном=0,01—0,1 (большие значения номинального скольжения относятся к двигателям мощностью до 1 кВт).
По мере увеличения скольжения увеличивается частота токов в роторе и возрастает влияние на характеристику индуктивного сопротивления ротора. Изменение тока, определяемое в зоне малых скольжений в основном активным сопротивлением [см. формулу (25)], замедляется, и при некотором скольжении, называемом критическим sкр, достигается максимальное значение момента. При дальнейшем увеличении скольжения (уменьшении частоты вращения ротора) момент будет уменьшаться.
Критическое скольжение находится по формуле
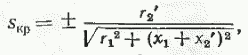
где знак плюс соответствует двигательному режиму работы, а минус — генераторному (как следует из рис. 20, генераторный режим соответствует области отрицательных скольжений).
Поскольку для двигателей мощностью более 1 кВт практически всегда r1<<(х1 + х’2), то формулу для критического скольжения можно упростить:

Теперь, подставляя значение s=sкр в формулу (41), получим выражение для максимального момента
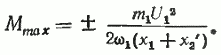
Взяв теперь отношение текущего значения момента к максимальному М/Мmax при условии r1≈0, получим
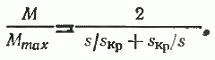
Формула (46) оказывается весьма удобной, так как позволяет построить механическую характеристику двигателя M=f(s) при известных значениях максимального момента и соответствующего ему критического скольжения. Задавая текущее значение скольжения в диапазоне 0<s≤1, решают уравнение (46) относительно текущего момента М. Можно поступить иначе — строить механическую характеристику в относительных единицах, т. е. получать характеристику M/Mmax=f (s).
Относительный максимальный момент определяет его перегрузочную способность, т. е. способность двигателя кратковременно выдерживать нагрузки, большие номинальной. В электрических машинах перегрузочная способность обозначает kм и определяется как
kм = Mmax/Mном (47)
Важное значение имеет пусковой момент, который можно рассчитывать по общей формуле (41) при подстановке в нее s= 1:
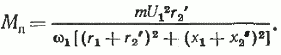
Относительное значение пускового момента kп определяет способность двигателя разгоняться до рабочей частоты вращения с полной нагрузкой на валу и определяется как
kп = Mп/Mном
В ряде случаев вместо (46) удобнее пользоваться формулой, в которой текущий момент двигателя отнесен не к максимальному, а к номинальному моменту. В этом случае
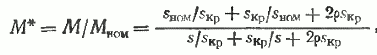
где sкр, sном — значения критического и номинального скольжения двигателя; ρ=r1/r’2 (для двигателей серии 4А с высотой оси вращения 56—132 мм пользуются значением ρ≈1,32).
Если пренебречь величиной r1 (т. е. положить ρ=0), то из (49) следует
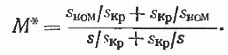
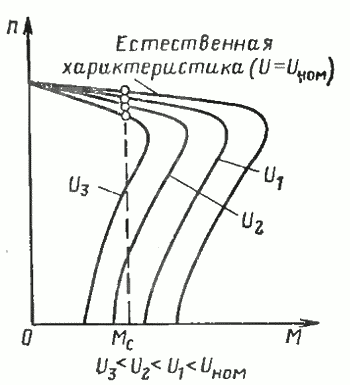
Анализ выражения (41) для электромагнитного момента показывает, чт момент зависит от квадрата напряжения сети, что является недостатком асинхронных двигателей. Так, при снижении напряжения на 10 % момент уменьшается на 19%, а при снижении напряжения на 20 % уменьшение момента составляет 36%. На рис. 21 изображены механические характеристики двигателя при номинальном питающем напряжении (естественная характеристика) и при пониженном напряжении.
При уменьшении напряжения, питающего двигатель, который работает под нагрузкой, его вращающий момент снижается. В результате этого происходит снижение частоты вращения двигателя. Частота снижается (и соответственно увеличивается скольжение) до тех пор, пока вращающий момент двигателя не станет равным статическому моменту сопротивления Мс, обусловленному (приводом (соответствующие частоты вращения показаны точками на механических характеристиках рис. 21). При сильном уменьшении напряжения может случиться, что максимальный момент окажется меньше момента сопротивления Мс. В этом случае двигатель опрокидывается, т. е. его частота вращения уменьшается и в конце концов он останавливается. При заторможенном роторе по обмоткам двигателя протекают большие токи, и во избежание аварии сам двигатель должен быть отключен от сети (эти функции выполняет тепловая защита).
Рис. 21. Механические характеристики асинхронного двигателя при различных значениях питающего напряжения
Рассмотрим уравнение движения ротора синхронной машины. Движение вращающейся части энергоагрегата (ротор генератора) описывается, согласно второму закону Ньютона.
Второй закон Ньютона — дифференциальный закон движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил. Второй закон Ньютона в его наиболее распространённой формулировке утверждает, что в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).
Применительно к вращающемуся ротору данный закон записывается в следующем виде:

где — угловое ускорение ротора генератора (или вала),
— момент инерции ротора,
— небаланс моментов, действующих на вал.
Уравнения для баланса моментов на валу записывается в следующем виде
где — вращающий момент, который создается турбиной
— момент сопротивления, обусловленный трением в подшипниках и сопротивлением охлаждающей среды
— электромагнитный момент, обусловленный электрической нагрузкой генератора и отражающий взаимодействие между магнитными системами статора и ротора.
Угловое ускорение ротора генератора определяется через производную скорости вращения вала синхронной машины
по следующей формуле:
С учетом введённой ранее формулы для скольжения 
В результате исходное уравнения движения ротора синхронной машины перепишется в следующем виде:
Момент сопротивления составляет около 3% от номинального момента, в целях упрощения уравнений часто не учитывается, в результате уравнение принимает следующий вид:
Выразим все составляющие этого уравнения в системе относительных единиц. Для этого разделим правую и левую его части на базисный момент, который определяется по следующей формуле:
Данное выражение перепишется в следующем виде:
Введем в уравнение движения ротора синхронной машины новую переменную — механическую инерционную постоянную ротора . С учетом новой переменной уравнение может быть переписано следующим образом:
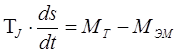
где — механическая инерционная постоянная, сек.;
— ,сек./рад.;
— вращающий момент, который создается турбиной, о.е.;
— электромагнитный момент, о.е.
Механическая инерционная постоянная агрегата
Механическая инерционная постоянная ротора – постоянная инерции ротора (вращающейся части агрегата), имеющая размерность времени и численно равная промежутку времени, в течение которого ротор разгоняется из состояния покоя до номинальной скорости вращения под действием номинального вращающего момента. В большинстве случаев данная переменная определяется значением в следующем диапазоне: 5…12 сек.
Механическая инерционная постоянная ротора определяется следующим образом:
— момент инерции ротора синхронной машины, кг·м²;
— маховый момент, кг·м²;
— номинальная угловая скорость вращения ротора, рад/с;
— номинальная полная мощность генератора, Вт = Дж / с = кг·м²/с.
В современных справочниках обычно можно найти маховый момент в т·м², скорость вращения в оборот/мин, а номинальную мощность в МВт. С учетом этого формула для расчета механической постоянной времени агрегата будет выглядеть так:
где — маховый момент генератора (двигателя), т·м²;
— частота вращения ротора, об/мин;
— номинальная полная мощность генератора, МВт.
При расчете механической инерционной постоянной агрегата необходимо пользоваться общим маховым моментом, который состоит из суммы махового момента генератора (двигателя), момента турбины и момент других элементов, таких как редуктор.
Для турбогенераторов момент инерции турбины примерно равен моменту инерции генератора, поэтому при расчете постоянной механической инерции агрегата, состоящего из генератора и турбины, можно значение постоянной механической инерции генератора увеличить в два раза (приближенный способ).
Следует отметить, что моменты инерции гидротурбин составляют примерно 10% момента инерции присоединенных к ним гидрогенераторов.
В качестве примера, выполним расчет постоянной механической инерции агрегата, который состоит из турбогенератора типа ТВФ-60-2 и турбины.
Параметры турбогенератора типа ТВФ-60-2:
,
,
,
Постоянная механическая инерции генератора определяется в следующем виде:
Постоянная механическая инерции агрегата, который состоит из генератора и турбины, определяется упрощено в следующем виде:
В некоторых программных комплексах вместо механической инерционной постоянной агрегата используют понятие постоянной инерции агрегата
, которая эквивалентна механической постоянной инерцией
и определяется по следующей формуле:
Вращающий момент, который создается турбиной
Рассмотрим, как связан момент турбины и мощности в относительных единицах. Момент турбины выражается через переменные: скорость вала синхронной машины и мощность синхронной машины.

Разделим данное выражение на базисный момент 
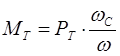
С учетом выражения для скольжения 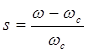
Электромагнитный момент
Электромагнитная мощность статорной цепи синхронной машины выражается через следующую формулу
Преобразуем правую часть выражения к системе oqd.
В связи с тем, что в синхронной машине нейтраль — изолирована, то нулевых составляющих тока нет.
Запишем уравнения для статорной цепи в осях d,q в именованных единицах:
С учетом данного выражения перепишем уравнение для электромагнитной мощности.
Пренебрегая производными потока, уравнение для электромагнитной мощности записывается в следующем виде (в именованных единицах):
Разделим данное выражение на базисную мощность , в результате получим выражение, записанное в относительных единицах (о.е.):
С учетом выражения для скольжения 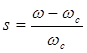
В результате электромагнитный момент перепишется в следующем виде:















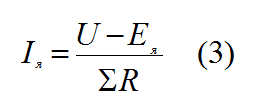



 – постоянная момента, Н∙м/А,
– постоянная момента, Н∙м/А, — жесткость механической характеристики электродвигателя постоянного тока
— жесткость механической характеристики электродвигателя постоянного тока

 — механическая постоянная времени, с
— механическая постоянная времени, с