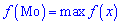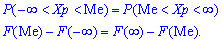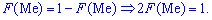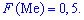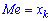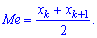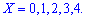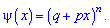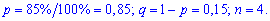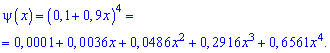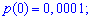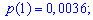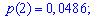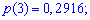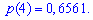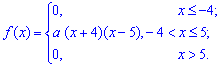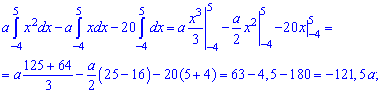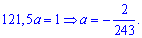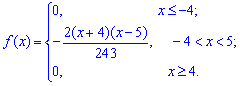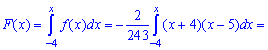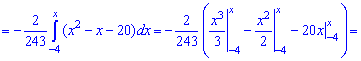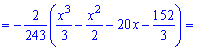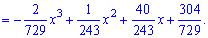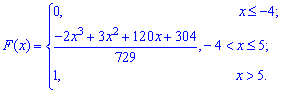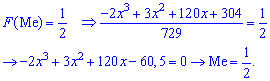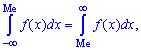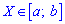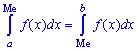Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
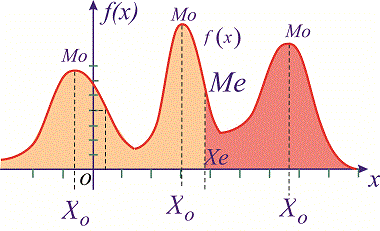
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
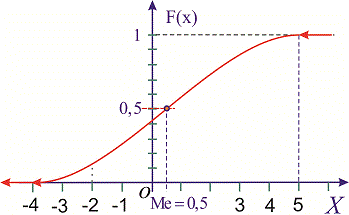
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике — мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Вводится лишь для НСВ, хотя
формально ее можно определить и для
ДСВ.
Определение 42. Медианой непрерывной
случайной величины называется такое
ее значение х = Ме, относительно
которого равновероятно получение
большего или меньшего значения случайной
величины, т. е. для которого справедливо
равенство:
,
( для НСВ безразлично
или
)
(по определению функции распределения).
Таким образом, медиана – это корень
уравнения
:
.
(3)
Геометрически: медиана – это
абсцисса точки, в которой площадь,
ограниченная кривой распределения,
делится пополам.
Замечание. В случае симметричного
модального распределения медиана
совпадает с мат. ожиданием и модой.
Когда медиана входит в формулы как
определенное число, то ее обозначают
hX.
Пп 2. Моменты
Данные характеристики описывают
некоторые свойства распределения
СВ. В механике, например, для описания
распределения масс существуют статические
моменты, моменты инерции…
Определение 43. Начальным моментом
s – того порядка для
ДСВ и НСВ называется математическое
ожидание s – той
степени этой случайной величины:
.
Замечание. При s
= 1
,
т. е. математическое ожидание – это
первый начальный момент.
а) Для дискретных случайных
величин:
.
(4)
Замечание. Определение совпадает
с определением начального момента
порядка s в механике,
если на оси (Ох) в точках х1 ,
х2, …,хn
сосредоточены соответственно
массы р1, р2 , …, рn.
b) Для
непрерывных случайных величин:
.
(5)
Определение 44. Центрированной
случайной величиной, соответствующей
величине Х, называется отклонение
случайной величины Х от ее
математического ожидания:
.
Рассмотрим математическое ожидание
центрированной ДСВ:
.
Аналогично, для НСВ
.
Центрирование СВ равносильно переносу
начала координат в среднюю, центральную
точку, абсцисса которой равна
математическому ожиданию.
Определение 45. Моменты центрированной
случайной величины называются центральными
моментами.
Определение 46. Центральным моментом
s – того порядка для
ДСВ и НСВ называется математическое
ожидание s – той
степени соответствующей центрированной
случайной величины:
.
а) Для дискретных случайных
величин:
. (6)
b) Для
непрерывных случайных величин:
.
(7)
Замечание. Для любой СВ центральный
момент 1-го порядка
равен
0:
,
так как мат. ожидание центрированной
СВ равно 0.
Рассмотрим подробнее центральные
моменты 2, 3, 4 порядков и выведем
соотношения, связывающие начальные и
центральные моменты.
– дисперсия
Определение 47. Дисперсией случайной
величины Х D[X]
называется мат ожидание квадрата
соответствующей центрированной случайной
величины:
а) Для дискретных случайных
величин: D[X]
=
.
(8)
b) Для
непрерывных случайных величин:
D[X]
=
.
(9)
Дисперсия случайной величины –
характеристика рассеивания,
разбросанности значений случайной
величины около ее мат. ожидания.
Когда дисперсия входит в формулы как
определенное число, то ее обозначают
DX.
Механическая интерпретация
D[X]:
Дисперсия – момент инерции заданного
распределения масс относительно центра
тяжести (мат. ожидания).
Рассмотрим ДСВ. (Для НСВ получаем
аналогично)
.
– связь между начальным и центральным
моментом 2-го порядка. (10)
Свойства
.
1.
,
где С – постоянная.
2.
.
3.
.
4.
для независимых СВ.
5.
,
a, b
– постоянные.
Замечание. D[X]
имеет размерность квадрата случайной
величины. Для более наглядной характеристики
рассеивания удобнее пользоваться
величиной, размерность которой совпадает
с размерностью случайной величины. Для
этого из D[X]
извлекают корень:
,
(11)
где
– среднее квадратическое отклонение
или стандарт случайной величины
Х.
Когда среднее квадратическое входит
в формулы как определенное число, то
его обозначают
.
Замечание. Математическое ожидание
и дисперсия характеризуют наиболее
важные черты распределения: его положение
и степень разбросанности. Для более
подробного описания применяются моменты
высших порядков.
– асимметрия
Асимметрия случайной величины –
характеристика асимметрии или
скошенности распределения значений
случайной величины.
Теорема. Если распределение
симметрично относительно мат. ожидания
(т. е. масса распределена симметрично
относительно центра тяжести), то все
моменты нечетного порядка (если они
существуют) равны нулю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мода и медиана функции плотности распределения f(x)
Задача 5. Плотность распределения вероятностей случайной величины Х имеет вид
1. Найти:
а) параметр распределения С (в виде дроби);
а) математическое ожидание M(X);
б) дисперсию D(X) и среднее квадратическое отклонение σ(Х);
в) функцию распределения F(x) случайной величины X;
г) моду M0;
д) медиану Me;
е) вероятность осуществления неравенств и
.
2. Построить графики функций f(x) и F(x). Изобразить на графике функции f(x) найденные характеристики и вероятности.
Решение находим с помощью калькулятора.
Случайная величина Х задана плотностью распределения f(x):
0, x ≤ 0
2•A(8/5-x), 0 < x < 8/5
0, x ≥ 8/5
Найдем параметр A из условия:

или
64/25*A-1 = 0
Откуда,
A = 25/64
Поскольку находили квадрат A, то
а) Математическое ожидание.

б) Дисперсия.
= -25/128•(8/5)4+5/12•(8/5)3 — (-25/128•04+5/12•03) — (8/15)2 = 32/225
Среднеквадратическое отклонение.
в) Функция распределения F(x) случайной величины X.

г) Мода M0.
Модой M0(X) называют то возможное значение X, при котором плотность распределения имеет максимум.
Построим график функции плотности распределения.
Как видим, максимум функции соответствует x = 0.
Mo( 0) = 2•25/64(8/5-0) = 5/4
д) Медиана Me.
Медианой Me(X) называют то возможное значение X, при котором ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Необходимо найти такое x, при котором функция распределения равна ½.
Решая уравнение:
получаем:
Поскольку функция ограничена на интервале (0; 1,6), то искомое значение x = 0,46.
Построим график функции распределения.
е) Вероятность осуществления неравенств и
.
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Тема 31-32: «Математическое ожидание
и его свойства»
Цель: рассмотреть числовые характеристики дискретной
случайной величины, вывести формулы и обозначения, учить решать задачи.
Функция распределения случайной дискретной величины
позволяет наиболее полно охарактеризовать рассматриваемую случайную величину.
Однако при решении многих задач проще указать числовые характеристики случайной
величины, чем соответствующий закон распределения. К важнейшим числовым
характеристикам случайной величины относятся: мода, медиана, математическое
ожидание, дисперсия и среднеквадратическое отклонение.
1)
Модой ДСВ называется такое
значение дискретной случайной величины, вероятность которого наибольшая.
Обозначается: Мо(х)
Значение случайной величины,
вероятность которой минимальная. Называется антимодой.
Пример 1. Закон распределения СВ задан таблицей
|
х |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
р |
|
|
|
|
|
|
|
|
|
Наибольшая вероятность р = , следовательно мода Мо(х) = 7, антимода равна 2.
Пример 2. При подбрасывании одного игрального кубика
составить ряд выпадения граней
|
х |
1 |
2 |
3 |
4 |
5 |
6 |
|
р |
|
|
|
|
|
|
Мода
не может быть указана, так как вероятность выпадения каждой грани одинакова.
Пример
3. По наблюдениям метрологов, среднесуточная температура в первой половине
февраля имела следующий ряд распределения: -18, -15, -18, -18, -15, -12. -12.
-5, -10, -7, -12, -18, -20,-15, -12. Составить закон распределения ДСВ –
среднесуточной температуры и найти моду.
Решение:
Составим закон распределения ДСВ — среднесуточной температуры, ранжируя ее
значения в порядке возрастания:
|
х |
-20 |
-18 |
-15 |
-12 |
-10 |
-7 |
-5 |
|
р |
|
|
|
|
|
|
|
В
данном случае наибольшую вероятность р = имеют два значения ДСВ: х=-18 и х=-12. Значит мода ДСВ х равна
Мо(х)=-12 и Мо(х)=-18.
Моду как характеристику ДСВ часто используют в социологических исследованиях,
например при определении рейтинга популярности того или иного политического
деятеля или певца. При этом в качестве ДСВ выступает число голосов, отданных,
например, за любимого певца при социологическом опросе .
2)
Медианой
ДСВ
называется среднее по положению в пространстве событий значение ДСВ.
Обозначается Ме(х)
Пример:
Учет производительности труда станочников цеха №3 за смену задан рядом
распределений:
|
Номер по списку |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
производительность |
52 |
52 |
53 |
54 |
56 |
57 |
57 |
57 |
Найти
моду и медиану ДСВ х.
Решение:
мода Мо(х) = 57 (самая «модная» производительность труда)
т.к.
число столбиков четное то медиану вычисляем как среднее арифметическое ДСВ
Ме(х)=
Для
нахождения медианы ранжирование ряда распределения является обязательным
условием.
Одна из самых важных характеристик ДСВ – математическое ожидание.
3)
Математическим
ожиданием ДСВ
называется сумма произведений значений случайной величины на их вероятности.
Обозначается М(Х).
Не
любая ДСВ может имеет математическое ожидание.
Свойства математического ожидания.
1)
Математическое
ожидание постоянной величины равно этой постоянной М(С)=С=const
2)
Постоянный
множитель можно выносить за знак математического ожидания: М(kX)=kМ(Х), k—const;
3)
Математическое
ожидание суммы случайных величин равно сумме их математических ожиданий: М(х +
у)=М(х) +М(у);
4)
Математическое
ожидание произведения независимых случайных величин равно произведению их
математических ожиданий: М(ху)=М(х)М(у).
Математическое ожидание можно найти всегда, если задан
закон распределения ДСВ.
Задача
1. Найти математическое ожидание произведения двух независимых случайных
величин Х и У, если известны их законы распределения.
|
у |
1 |
2 |
3 |
4 |
|
р |
0.3 |
0,1 |
0,25 |
0,35 |
М(х)
= 3*0,3 + 5*0,5 + 7*0,2 =4,8
М(у)
= 1*0,3 +2*0,1 + 3*0,25 + 4*0,35 = 2,65
М(ху)=М(х)М(у)=4,8*2,65=12,72.
Ответ:
12,72
Задача
2. Из 100 лотерейных билетов в тридцати выигрыш составляет 100 тыс. р., в
десяти – 200 тыс. р., в пяти – 300 тыс.р., в одном -1 млн.р. Найти числовые
характеристики выигрыша.
Решение:
СВ х –выигрыш – принимает значения х1=0, х2=100 тыс.р, х3=200
тыс.р., х4=300 тыс.р., х5=1 млн.р.
Вычислим
вероятности р1==0.54; р2 =
=0.3; р3 =
=0,1; р4 =
=0,05;
Р5
= =0,01. Составим закон распределения этой ДСВ
|
х |
0 |
100тыс. |
200 тыс. |
300 тыс. |
1 млн. |
|
р |
0,54 |
0,30 |
0,10 |
0,05 |
0,01 |
Мо(х)
= 0 ( т. К. наибольшая вероятность 0,54 )
Ме(х)
=200 тыс.
М(х)
= 0*0,54 + 100 тыс.р.*0,3 + 200 тыс.р.*0,1 +300 тыс.р.*0,05 + 1 млн.р*0,01=75
тыс.р.
Задача
3. Найти математическое ожидание случайной величины у = 5х + 9, если известно,
что М(х) =2,5
Решение:
зная свойства математического ожидания, имеем:
М(у)
= М(5х +9) = М(5х) +М(9) = 5М(х) +9 = 5*2,5 +9 =7,5 +9=16,5.
Решить
самостоятельно:
1.
Найти
математическое ожидание дискретной случайной величины, имеющей следующее
распределение:
А)
Б)
В)
2.
Дискретная
случайная величина Х принимает три возможных значения: х1=4 с
вероятностью р1=0,5; х2=6 с вероятностью р2=0,3
и х3 с вероятностью р3. Найти х3 и р3,
зная, что М(х) = 8.
3.
Дискретная
случайная величина имеет следующий закон распределения:
Математическое ожидание равно 3. Найти х1 и р3.
Построить многоугольник распределения.
4.
Найти
математическое ожидание величины Z, если:
А) Z = 3х +4 у; М(х)=2; М(у)=6;
Б) Z = 12х +3у; М(х)=0; М(у)=4.
Тема 33-34: «Дисперсия.
Среднеквадратическое отклонение»
Цель:
дать определения, ввести обозначение дисперсии и среднеквадратического
отклонения, учить вычислять эти величины.
Математического ожидания недостаточно для описания случайной величины. Для
более полной характеристики случайной величины надо оценивать рассеивание ее
возможных значений. Для характеристики рассеивания случайной величины и
предназначена дисперсия.
Дисперсией случайной величины Х
называется математическое ожидание квадрата отклонения ее возможных значений
от ее среднего значения.
Обозначается:
Д(х).
Д(х)=
М((х – М(х))2) или
Д(х)
= М(х2) – М2(х).
Дисперсия
числа появлений в n независимых испытаниях ( с
одинаковой вероятностью появления р события в каждом испытании и вероятности не
появления q) вычисляется по формуле Д(х)
= npq.
Пример1. Найти Д(х) случайной
величины, заданной следующим законом распределения:
|
х |
3 |
4 |
6 |
7 |
|
р |
0.2 |
0,25 |
0,35 |
0,2 |
Решение:
вычислим М(х) = 3*0,2 +4*0,25 + 6*0,35 + 7*0,2 = 5,1
Составим
закон распределения случайной величины х2
|
Х2 |
32=9 |
16 |
36 |
49 |
|
р |
0,2 |
0,25 |
0.35 |
0,2 |
М(х2)
= 9*0,2 + 16*0,25 + 36*0,35 +49*0,2 = 28,2
Д(х)
= М(х2) – М2(х) = 28,2 – 5,12 = 28,2 – 26,01 =
2,19
Ответ:
Д(х) =2,19
Пример
2. Найти
дисперсию ДСВ х – числа отказов элемента некоторого устройства в десяти
независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9.
Решение:
по условию n = 10; q =0.9 ; p = 0.1
D(x) = nqp = 10*0,9*0,1 = 0,9
Ответ:
Д(х) = 0,9
Свойства дисперсии.
1.
Д(х) 0 дисперсия любой случайной величины есть величина
неотрицательная.
2.
Дисперсия
постоянной величины С равна 0. Д(С) =0.
3.
Постоянный
множитель можно вынести за знак дисперсии, возведя его в квадрат. Д(Сх) = С2Д(х).
4.
Дисперсия
не меняется от смещения случайной величины Д(х – С)=Д(х).
5.
Дисперсия
суммы независимых случайных величин равна сумме дисперсий этих величин Д( х1
+ х2 + х3 +…+ хn) = Д(х1)+Д(х2)+Д(х3)+ …
+Д(хn)
Т.к. дисперсия имеет размерность квадрата случайной
величины, то это очень неудобно для наглядного представления степени
рассеивания случайной величины Х. Чтобы устранить этот недостаток, вводится
показатель степени рассеивания случайной величины Х, имеющий с ней одинаковую
размерность. Этот показатель называется среднеквадратическим отклонением и обозначается
σ.
квадратный из дисперсии этой
ДСВ.
σ=
Пример 3. Найти дисперсию и среднеквадратическое
отклонение, если ДСВ задана законом распределения.
Решение: Д(х) = М(х2) – М2(Х)
; М(х) = 4*0,2 + 5*0,3 + 10*0,5 =7,3
Составим таблицу для х2
|
х |
16 |
25 |
100 |
|
р |
0,2 |
0,3 |
0,5 |
М(х2) = 16*0,2 + 25*0,3 + 100*0,5 = 60,7
Д(х) = 60,7 – 7,32 =7,41; σ = =2,72
Ответ: 7,41; 2,72
Пример 4. Составить закон распределения ДСВ х,
принимающей значения х1 =1, х2 =3, Х3=4, если
известно, что М(х) = 2,3; Д(х) =1,21.
Составим систему трех уравнений с тремя неизвестными
Р1 + 3р2 + 4р3 =2,3;
Р1 +9р2 + 16р3 = 1,21
+2,32;
Р1 + р2 + р3 = 1
Решим систему и найдем р1 =0,4; р2
=0,5; р3 =0,1
Решить задачи самостоятельно:
1.
Найти М(х2)
дискретной случайной величины, заданной законом распределения:
А)
Б)
|
х |
0,2 |
0,5 |
0,6 |
|
р |
0,1 |
0,5 |
0,4 |
2.
Дан
перечень возможных значений дискретной значений величины: х1 = -1, х2
=0, х3 =1, а также известны М(х) = 0,1 и М(х2) =0,9.
Найти вероятности р1, р2. Р3.
3.
Найти
дисперсию и среднеквадратическое отклонение дискретной случайной величины, имеющей
следующее распределение:
А)
|
х |
-5 |
2 |
3 |
4 |
|
р |
0,4 |
0,3 |
0.1 |
0,2 |
Б)
В)
4.
Дискретная
случайная величина имеет только два возможных значения х1 и х2,
причем х1х2. Вероятность того, что Х принимает значение х1,
равно 0,6.
Найти закон распределения величины Х,
если М(х) = 1,4; Д(х) = 0,24.
Тема: Характеристики
непрерывной случайной величины.
Основные числовые характеристики: мода, медиана,
математическое ожидание, дисперсия.
1.
Модой
НСВ Х
называется такое ее значение, при котором плотность вероятности максимальная.
Случайная вероятность может иметь несколько мод.
С геометрической точки зрения мода –
значение аргумента Х, при котором график функции плотности распределения
принимает максимальное значение.
( находят моду через производную.
Надо исследовать функцию на интервале и найти точки максимума функции и
сравнить их со значением f(x) на границах интервала).
2.
Медианой
НСВ Х называют
такое ее значение µ, для которого равновероятно что случайная величина Х больше
или меньше µ.
Р(хµ) = р(х
µ) = 0,5
Т.е. медиана есть корень
алгебраического уравнения F(x) = 0,5 или
Интегрального уравнения
C геометрической точки зрения медиана делит
площадь под графиком функции плотности вероятности на две равные части.
3.
Математическим
ожиданием НСВ называется интеграл
М(Х) = в том случае если он существует.
С геометрической точки зрения
математическое ожидание случайной величины равно абсциссе центра тяжести
площади, ограниченной кривой распределения и осью абсцисс.
В случае, когда кривая
распределения симметрична относительно прямой
X = m математическое ожидание совпадает с этой абсциссой, и
математическое ожидание, мода и медиана равны между собой.
М(х) =Мо=Ме=µ.
4.
Дисперсию
НСВ х находят
по формуле D(x) = или
D(x)
Примеры:
Тема: «Теорема сложения совместных
событий»
Пусть в некотором испытании
рассматриваются два совместных случайных А и В, вероятности которых известны
ли могут быть найдены.
Теорема: Вероятность появления хотя бы одного
из двух совместных событий равна сумме вероятностей этих событий без
вероятности их совместного появления, т. е. р(А + В) = р(А) + р(В) – р(АВ)
Эту формулу можно применить и для двух несовместных
событий т. к. р(АВ) = 0.
Если А и В независимые р(а + В) = р(А) + р(В) –
р(А)*р(В)
Если А и В зависимые р(А + В) = р(А) + р(В) – р(А)* ра(в).
Пример 1: Два футболиста делают независимо друг от
друга по одному удару по воротам. Вероятность попадания первого футболиста
равна 0,8; второго – 0,9. Найти вероятность того, что произойдет хотя бы одно
попадание.
Решение: событие А- попадание первым футболистом
Событие В – попадание вторым футболистом
А + В – произойдет хотя бы одно попадание.
По теореме р(А + В) = 0.8 + 0, 9 – 0,8*0,9 =
Ответ:
Эту задачу можно решить другим способом:
Р() = 1 – р(А) = 1 – 0,8 =0,2
Р() = 1 – р(В) = 1 – 0,9 = 0,1
Р(А + В) = 1 – 0,2*0,1 =
Ответ:
Существует более общая формула для нахождения
вероятности суммы трех и большего числа совместных событий. А, В, С – события,
тогда
Р(А + В +С) = р(А) +р(В) + р(С) – р(АВ) – р (АС) –
р(ВС) + р(АВС), но решать задачу таким образом очень сложно, легче решать через
противоположные события.
Пример 2: Каждый из четырех стрелков независимо друг
от друга производит по одному выстрелу в мишень. Вероятности попадания равны:
0,7; 0,6; 0,8; 0,4. Определить вероятность того, что произойдет хотя бы одно
попадание.
Решение: пусть события А1 –попадет первый
стрелок, А2 – второй стрелок, А3 – третий стрелок, А4
– четвертый стрелок.
Для событий А1 +А2 +А3
+А4 противоположными являются события 1
2
3
4 – все промахнутся.
Р(1) = 1 – р(А1) = 1 – 0,7 = 0.3
Р(2) = 1 – р(А2) = 1 – 0,6 = 0,4
Р(3) = 1 – р(А3) = 1 – 0,8 = 0,2
Р(4) 1 – р(А4) = 1 – 0,4 = 0,6
Р(А1+А2 +А3 + А4)
= 1 – 0,3*0,4*0,2*0,6 =
Ответ:
Таким способом решаются задачи в которых есть слова
«хотя бы».
Решить задачи самостоятельно:
1.
Стрелок
производит один выстрел в мишень, состоящую из центрального круга и двух
концентрических колец. Вероятность попадания в круг и кольца соответственно
равны 0,1; 0,3; 0,4. Определить вероятность попадания в мишень.
2.
В
двух группах имеется по 25 студентов; в первой – 5 отличников. Во второй -8. Из
каждой группы выбирается по одному студенту. Какова вероятность того, что они
отличники?
3.
Вероятности
вынуть белый шар из двух ящиков равны соответственно 0,8; 0,6. Из обоих ящиков
вынимается по одному шару. Какова вероятность того, что хотя бы один из вынутых
шаров белый?
4.
В
двух коробках лежат по 20 одинаковых по форме карточек. Из них в первой – 5
карточек зеленого цвета, во второй -10. Наугад выбирают из каждой коробки по
одной карточке. Какова вероятность того, что хотя бы одна карточка будет не
зеленого цвета?
5.
Из
колоды в 32 карты наугад выбирают 4 карты. Найдите вероятность того, что среди
отобранных карт окажется хотя бы один туз.
6.
На
стеллаже в библиотеке стоят 15 учебников, причем 5 из них в переплете.
Библиотекарь берет наудачу три учебника. Найдите вероятность того, что хотя бы
один из взятых учебников будет в переплете.
Тема: « Формула полной вероятности.
Формула Байеса».
Чтобы вывести формулу полной вероятности рассмотрим задачу:
Задача
1. В трех одинаковых ящиках находятся: в первом – 3 белых и 2 черных шара; во
втором – 6 белых и 4 черных шара; в третьем – 2 белых и 3 черных. Из случайно
выбранного ящика наугад вынимают шар. Какова вероятность того, что этот шар
белый?
Решение:
А – вынутый белый шар.
В1
– шар вынут из первого ящика;
В2
–шар вынут из второго ящика;
В3
– шар вынут из третьего ящика.
Р(В1)
=р(В2) =р(В3) = Событие А должно произойти с одним из событий В1,
В2 или В3.
Р(А)
= р(В1)рВ1(А) + р(В2) рВ2(А) + р(В3)
рВ3(А);
Рв1(А)
=; рв2(А) =
; рв3(А) =
Р(А)
=
Ответ:
при решении этой задачи была использована формула полной вероятности.
Теорема: (формула полной вероятности)
Пусть
В1, В2, … Вn – полная группа событий для некоторого испытания, и событие
А может произойти вместе с одним из событий полной группы. Тогда справедлива
формула:
Р(А)
= р(В1) рв1(А) + р(В2) рв2р(А) + …
+ р(Вn) рвnр(А), В1, В2,
… Вn -называются гипотезами.
Решить
задачу: Для приема зачета преподаватель приготовил 50 задач: 20 по
дифференциальному и 30 по интегральному исчислению. Для получения зачета
студент должен должен решить первую попавшуюся ему задачу. Какова вероятность
для студента получить зачет, если он знает решение 18 задач по
дифференциальному и 15 по интегральному исчислению.
Решение:
А – студент сдаст зачет; В1 – попадет задача по дифференциальному
исчислению; В2 – по интегральному исчислению.
Р(В1)
= = 0,4 р(В2) =
= 0,6; рв1(А) =
= 0,9; рв2(А) =
= 0,5;
Р(А)
= 0,4
Ответ:
0,66
Решим
задачу 1. С измененным условием: Предположим, что шар вынут и известно, что он
оказался белым, т. е. событие А произошло. Какова вероятность того, что шар
был вынут из первого ящика?
Р(В1)
– это вероятность события вычисленная до испытания;
Рв1(А)
– вероятность события В1 вычисленная при условии, что событие А уже
произошло.
Для
решения задачи использовали формулу:
Рвi(А ) = ; i =
1, 2, … , n. Формула Байеса. ( применяется, когда
известно, что событие А уже произошло).
Решить
задачу: Из имеющихся на складе кинескопов 30 % изготовлены на заводе №1,
остальные на заводе №2. Вероятность того, что кинескоп, изготовленный на заводе
№1 не выйдет из строя в течении гарантийного срока службы, равна 0.9, для
кинескопов с завода №2 эта вероятность равна 0,8. Случайным образом для поверки
со склада выбирают кинескоп, который выдержал гарантийный срок. Определить
вероятность того, что его изготовили на заводе №2.
Решение:
А – кинескоп выдержавший гарантийный срок;
В1
– завод №1; В2 – завод №2;
р(В1)
= 0,3; р(В2) = 0,7; рв1(А) = 0,9; рв2(А)
= 0,8.
Р(А)
= 0,3
Рв2(А)
= =
( если надо найти рв1(А) = 1 – 0,67 = 0,33)
Ответ:
0,67
Решить
задачи самостоятельно:
1.
Имеется
два набора открыток. В первом наборе имеется 13 стандартных и 2 не стандартных
по размеру открытки; во втором – 8 стандартных и 2 нестандартных открытки.
Определить вероятность того, что взятая наудачу открытка (из случайно
выбранного набора ) стандартная.
2.
В магазин
поступили две партии костюмов. В первой партии – 20 синих и 15 черных, во
второй -15 синих и 10 черных. Первая партия изготовлена заводом №1, вторая
-заводом №2. Покупатель купил синий костюм. Определить вероятность того, что
костюм изготовлен заводом №2.
3.
Представитель
фирмы при приеме двух партий некоторой продукции для контроля случайным образом
выбирает по одному изделию из каждой партии. Вероятность выбора бракованного
изделия из первой партии равна 0,1; из второй – 0,05. Найдите вероятность
того, что: а) оба выбранных изделия будут без брака; б) хотя бы одно выбранное
изделие без брака.
Схема Бернулли. Локальная и
интегральная формулы Муавра-Лапласа в схеме Бернулли.
На практике часто приходится иметь дело с многократным
повторением одного и того же испытания по возможности в одних и тех же
условиях. Например, 10 выстрелов по мишени при неизменных условиях стрельбы –
это десятикратное повторение одного испытания – выстрела по мишени.
Допустим, что выполняется n независимых одинаковых испытаний. Испытания независимы в
том смысле, что результаты одних испытаний не влияют на результаты других.
Одинаковые независимые испытания называются испытаниями
Бернулли, если в каждом испытании возможны только два исхода («успех» и
«неудача») и вероятности каждого из этих исходов постоянны.
Введем обозначения: р – вероятность «успеха», появления
события А.
q – вероятность
«неудачи», непоявление события А, тогда р + q = 1.
Пусть проводят n испытаний в которых событие А встречается m раз, и не встречается (n – m), то искомую вероятность можно вычислить по формуле Бернулли:
Рn(А = m) =
Пример:
Монету подбрасывают 6 раз. Какова вероятность того, что герб выпадет только два
раза?
Решение:
n = 6; m = 2; p = ( только два исхода орел и решка)
q = 1 – p =
1 – 0.5 = 0.5 p6(A = 2) =
Ответ:
Решить
самостоятельно: Вероятность попадания в цель для стрелка равна 0,6. Какова
вероятность из 10 выстрелов попасть ровно 4 раза. (ответ: 0,11)
Чем больше число n в задачах тем сложнее ее
вычислить. Это обстоятельство было отмечено еще в 18 веке математиками
занимающимися демографическими проблемами. Возникла необходимость получения
приближенной формулы для нахождения соответственно вероятности. Эта задача была
успешно решена для частного случая при р = 0,5 в 1730 году английским
математиком Абрахамом де Муавром и обобщена в1783 году французским математиком
Пьером Лапласом.
Локальная
теорема Муавра-Лапласа.
Если вероятность наступления события А в каждом из n независимых испытаний равна Р и
отлична от нуля и единицы, а число испытаний велико, то вероятность того, что
в n испытаниях событие А
наступит ровно m раз, приближенно равна
значению функции
Рn (А = m) , где
— находим в таблице П2 учебник Спирина стр.265-267.
Пример:
Вероятность того, что сошедшая с конвейра деталь окажется бракованной, равна
0,1. Найти вероятность того, что 600 деталей, сошедших с конвеера, 87 деталей
будут бракованными.
Решение:
р = 0,1, n = 600 m = 87
q = 1 – 0.1 = 0.9 P600(A =87)
Ответ:
0,000068
Решить
самостоятельно: Вероятность поражения мишени стрелком при одном выстреле 0,7.
Найти вероятность того, что при 20 выстрелах стрелок поразит мишень 15 раз.
Теорема
Пуассона: Если
вероятность р появления события А в каждом испытании постоянна, но близка к
нулю, число независимых испытаний Бернулли достаточно велико, то вероятность
того, что в этих n испытаниях событие А
наступит ровно m раз, приближенно
равна:
Рn(А = m) = формула Пуассона.
Пример:
Завод отправил в магазин 5000 исправных телевизоров. Вероятность того, что во
время пути произойдет повреждение телевизора, равна 0,0002. Какова вероятность
того, что во время пути произойдет повреждение у трех телевизоров.
Решение:
n = 5000 m = 3 p = 0.0002 λ = 5000
Р5000(А
=3) =
Ответ:
0,062
Интегральная
теорема Лапласа.
Вероятность
того, что в независимых испытаниях, в каждом из которых вероятность появления
события А равна р. Событие А наступит не менее m1 раз и не более m2 раз, приближенна равна:
Рn(m1
Пример:
Вероятность того, что деталь не прошла проверку ОТК, равна 0,1. Найти
вероятность того, что среди случайно отобранных 500 деталей проверку не
пройдут от 70 до 100 деталей.
Решение:
n = 500 m1=70 m2=100 p = 0.1
q =1 – p = 1
– 0.1 = 0.9
P500(
в таблице стр. 267 Спирина)
Ответ:
0,0013
Решить
самостоятельно: Производится 600 выстрелов. Вероятность промаха при одном
выстреле равна 0,015. Найти вероятность того, что число промахов будет не
меньше 7 и не больше 9.
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой 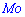
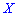
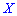
В зависимости от вида функции 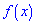
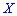
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой 
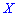
Графически мода и медиана изображенные на рисунке
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 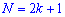
в случае четного количества 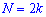
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 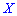
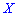
Решение. Случайной величина может принимать значения
Вероятности появления значений определяем по образующей функцией
Для заданной задачи входные величины принимают значения
Искомые вероятности входят множителями при степенях аргумента
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 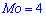
Пример 2. По заданной плотностью вероятностей
найти параметр 
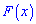
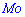
Решение. Применяя условие нормирования выполняем интегрирование
после того определяем параметр
Плотность вероятностей, учитывая найденное значение будет иметь вид
а ее график изображен на рисунке ниже
Из графика плотности вероятностей видим, что мода принимает значение 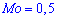

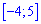
Функция распределения иметь следующий вид
а ее график будет иметь вид
Для определения медианы случайной величины 
Медиану 
для дискретной случайной величины из промежутка
Таким образом медиану 
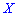
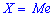
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.